referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Статистические расчеты
Вариант 1.
Задача №1
Имеются данные по 16 рабочим:
| № п/п | Стаж работы, лет | Выработка изделий, шт. | № п/п | Стаж работы, лет | Выработка изделий, шт. |
| 1 | 6 | 50 | 9 | 12 | 72 |
| 2 | 7 | 49 | 10 | 4 | 39 |
| 3 | 9 | 60 | 11 | 5 | 41 |
| 4 | 8 | 55 | 12 | 12 | 70 |
| 5 | 1 | 34 | 13 | 16 | 80 |
| 6 | 9 | 58 | 14 | 10 | 62 |
| 7 | 3 | 46 | 15 | 10 | 65 |
| 8 | 7 | 58 | 16 | 14 | 82 |
С целью изучения зависимости между стажем работы и выработкой рабочих произведите группировку рабочих по стажу работы, выделив три группы с равными интервалами. По каждой группе и целом подсчитайте:
А) число рабочих;
Б) стаж работы – в целом и в среднем на одного рабочего;
В) выработку изделий – в целом и в среднем на одного рабочего.
Решение:
1-я гр стаж работы от 0 до 5,3 лет | Стаж работы, лет | Выработка изделий, шт. | ||||
| 1 | 34 | |||||
| 3 | 46 | |||||
| 4 | 39 | |||||
| 5 | 41 | |||||
| Число рабочих в группе: | 4 | |||||
| Стаж работы в целом по группе, лет | 13 | |||||
| Стаж работы на 1-го рабочего группы, лет | 3,25 | |||||
| Выработка изделий в целом по группе, шт | 160 | |||||
| Выработка изделий на 1-го рабочего группы, шт | 40 | |||||
2-я гр стаж работы от 5,4 до 10,6 лет | Стаж работы, лет | Выработка изделий, шт. | ||||
| 6 | 50 | |||||
| 7 | 49 | |||||
| 9 | 60 | |||||
| 8 | 55 | |||||
| 9 | 58 | |||||
| 7 | 58 | |||||
| 10 | 62 | |||||
| 10 | 65 | |||||
| Число рабочих в группе: | 8 | |||||
| Стаж работы в целом по группе, лет | 66 | |||||
| Стаж работы на 1-го рабочего группы, лет | 8,25 | |||||
| Выработка изделий в целом по группе, шт | 457 | |||||
| Выработка изделий на 1-го рабочего группы, шт | 57,125 | |||||
3-я гр стаж работы от 10,6 до 16 лет | Стаж работы, лет | Выработка изделий, шт. |
| |||
| 12 | 72 |
| ||||
| 12 | 70 |
| ||||
| 16 | 80 |
| ||||
| 14 | 82 |
| ||||
| ||||||
| Число рабочих в группе: | 4 |
| ||||
| Стаж работы в целом по группе, лет | 54 |
| ||||
| Стаж работы на 1-го рабочего группы, лет | 13,5 |
| ||||
| Выработка изделий в целом по группе, шт | 304 |
| ||||
| Выработка изделий на 1-го рабочего группы, шт | 76 |
| ||||
| Число рабочих всего: | 16 |
| ||||
| Стаж работы в целом, лет | 133 |
| ||||
| Стаж работы на 1-го рабочего в среднем, лет | 8,3125 |
| ||||
| Выработка изделий в целом, шт | 921 |
| ||||
| Выработка изделий на 1-го рабочего в среднем, шт | 57,5625 |
| ||||
Исходя из полученных данных, можно сделать вывод о том, что выработка изделий напрямую зависит от стажа рабочего: самая продуктивная работа у рабочих, чей стаж превышает 10 лет.
Задача №2.
Имеются следующие данные о численности и заработной плате персонала по двум организациям:
| № п/п | Базисный период | Отчетный период | ||
| Среднемесячная зарплата, руб. | Число работающих, чел. | Среднемесячная зарплата, руб. | Фонд заработной платы, тыс руб. | |
| 1 | 6500 | 210 | 6800 | 139,5 |
| 2 | 7100 | 350 | 7450 | 253,5 |
Вычислите среднемесячную заработную плату по двум предприятиям:
1. за базисный период;
2. за отчетный период.
Сравните полученные показатели и сделайте вывод.
Решение:
Определим фонд заработной платы по двум предприятиям за базисный период: 6500*210+7100*350 = 3 850 тыс. руб.
Общее число работающих по двум предприятиям: 210 + 350 = 560 чел.
Среднемесячная зарплата за базисный период: 3850000 / 560 = 6 875 руб.
Т.е. за базисный период рабочие второго предприятия получали заработную плату выше, чем средняя по двум предприятиям за данный период.
Среднее число работающих в отчетном периоде по двум предприятиям: 139 500 / 6 800 + + 253 500 / 7 450 ≈ 54 чел
Среднемесячная зарплата за отчетный период: (139500+253500) / 54 ≈ 7 278 руб. Т.о., в отчетном периоде ситуация аналогична базисному периоду.
Задача №3.
Население города по возрасту распределяется следующим образом:
| Возраст, лет | Удельный вес населения (% к итогу) | |
| 1 | 0-9 | 17,00 |
| 2 | 10-19 | 20 |
| 3 | 20-29 | 18 |
| 4 | 30-39 | 14 |
| 5 | 40-49 | 10 |
| 6 | 50-59 | 9 |
| 7 | 60-69 | 7 |
| 8 | 70 и старше | 5 |
По данным таблицы исчислите:
1. средний возраст населения города;
2. моду, медиану.
Сделайте выводы.
Решение:
1.
| Возраст, лет | Удельный вес населения (% к итогу) | Средний возраст группы | Удельный вес | |
| 1 | 0-9 | 17,00 | 4,5 | 0,77 |
| 2 | 10-19 | 20 | 14,5 | 2,90 |
| 3 | 20-29 | 18 | 24,5 | 4,41 |
| 4 | 30-39 | 14 | 34,5 | 4,83 |
| 5 | 40-49 | 10 | 44,5 | 4,45 |
| 6 | 50-59 | 9 | 54,5 | 4,91 |
| 7 | 60-69 | 7 | 64,5 | 4,52 |
| 8 | 70 и старше | 5 | 74,5 | 3,73 |
| Средний возраст населения города: | 30,50 | |||
2.Найдем моду по формуле:
М = 19 + (9* (20 – 17) / ((20 – 17) + (20 – 18)) = 19 + 27 / 5 = 24,4года
24,4 года - это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
Найдем медиану по формуле:
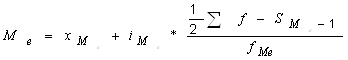
Ме = 39 + 9 * (50 – 55) / 14 = 39 – 5 / 14 * 9 = 35,78 лет
35,78 - варианта, находящаяся в середине ряда распределения, она делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.
Задача №4.
Имеются следующие данные об остатках вкладов в одном из отделений сберегательного банка в первом полугодии 2008 г. (тыс. руб.)
на 01.01 | на 01.02 | на 01.03 | на 01.04 | на 01.05 | на 01.06 | на 01.07 |
| 880 | 883 | 881 | 900 | 910 | 918 | 920 |
Исчислите средние остатки вкладов в сберегательном банке:
1. за первый квартал;
2. за второй квартал;
3. за полугодие в целом.
Решение:
Среднемесячные остатки вкладов за первый квартал (с 01.01 по 01.04):
(883 + 881 + 900) / 3 = 888 тыс. руб.
Среднемесячные остатки вкладов за второй квартал (с 01.04 по 01.07):
(910 + 918 + 920) / 3 = 916 тыс. руб.
Среднемесячные остатки вкладов за полугодие (с 01.01 по 01.07):
(883 + 881 + 900 + 910 + 918 + 920) / 6 = 902 тыс. руб.
Задача №5.
Имеются данные о продаже картофеля по двум рынкам:
| Рынок | Цена 1 кг., руб. | Продано картофеля, тонн | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| 1 | 13 | 12,5 | 100 | 150 |
| 2 | 12,2 | 12 | 150 | |