Розрахунки надійності електронної апаратури
РОЗРАХУНКИ НАДІЙНОСТІ ЕЛЕКТРОННОЇ АПАРАТУРИ (ЕА)
1. Аналітичний метод розрахунку надійності
Під розрахунком надійності розумітимемо визначення числових значень показників за будь-якими вихідними даними. У зв’язку із включенням кількісних показників надійності у технічні вимоги на апаратуру виникла необхідність не тільки теоретичної, а й практичної перевірки виконання цих вимог за статистичними даними. Вирішення цієї задачі потребує розробки визначених математичних методів, а також проведення ряду організаційних заходів по збиранню статистичних даних у процесі експлуатації.
Розрізняють аналітичні методи розрахунків при проектуванні апаратури і розрахунки надійності за статистичними даними, отриманими у процесі експлуатації або випробовування.
Загальні вимоги до надійності ЕА встановлюються з урахуванням призначення, умов експлуатації та наслідків відмов апаратури. Під час розробки завдання на проектування у технічне завдання (ТЗ) зазвичай включають такі питання:
- перелік показників надійності;
- кількісні значення показників надійності;
- терміни розрахунків показників надійності на етапі проектування;
- методика, умови та місце випробовувань апаратури на надійність;
- точність оцінки результатів випробовувань на надійність.
Складна радіоелектронна апаратура, в тому числі й побутова, складається з окремих блоків, модулів, елементів, від надійності яких залежить реалізація встановлених параметрів надійності РЕА в цілому. Отже, необхідно розподілити вимоги до надійності окремих частин апаратури, виходячи з загальних вимог до надійності РЕА в цілому.
Ймовірність безвідмовної роботи системи за час t:
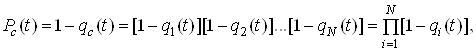 (1)
(1)
де qc – ймовірність відмови системи (апаратури);
qi – ймовірність відмови модуля (блока);
N – кількість модулів (блоків).
Під час розгляду методів розрахунку надійності вважатимемо, що ніяких попередніх заходів з її підвищення не вжито, елементи, які використовуються, типові і з’єднані між собою послідовно.
Залежність між ймовірністю безвідмовної роботи елемента та інтенсивністю його відмов при розподілі часу безвідмовної роботи за довільним законом визначається виразом:
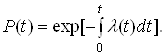 (2)
(2)
Ймовірність безвідмовної роботи апаратури з послідовним з’єднанням елементів за надійністю можна показати у вигляді добутку ймовірностей безвідмовної роботи її елементів:
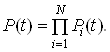 (3)
(3)
Замінивши Pi(t) його значенням з попереднього рівняння, запишемо:
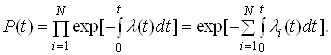 (4)
(4)
Позначивши:
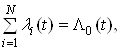
отримаємо:
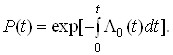 (5)
(5)
Як правило, будь-яка апаратура складається з великої кількості груп різних елементів, які мають приблизно однакову надійність. Тоді для апаратури, яка має k груп елементів, отримаємо інтенсивність відмов:
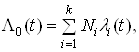
де Ni – кількість елементів у групі.
Підставивши отриманий вираз у формулу (5), маємо:
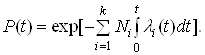 (6)
(6)
В окремому випадку, коли інтенсивність відмов можна вважати постійною в часі, тобто для експоненціального закону:
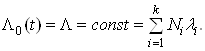
![]() (7)
(7)
Таким чином, ми отримали формулу ймовірності безвідмовної роботи апаратури при експоненціальному законі розподілу інтенсивності відмов.
Важливою властивістю експоненціального закону є те, що ймовірність безвідмовної роботи протягом заданого проміжку часу t не залежить від того, скільки часу прилад працював до того.
Середній час роботи до першої відмови (або напрацювання на відмову), показники ремонтопридатності та готовності ми розглядали у попередніх лекціях.
При розрахунках показників ремонтопридатності і готовності середня тривалість поточного ремонту зазвичай береться з досвіду експлуатації раніше створених аналогічних радіоелектронних засобів.
Таким чином, для аналітичного розрахунку надійності необхідно розподілити вимоги за надійністю окремих вузлів, блоків, виходячи із загальних вимог до надійності пристрою в цілому; мати дані про інтенсивності відмов елементів, закон розподілу відмов та середній час поточного ремонту.
2. Розрахунки надійності за статистичними даними
Для оцінки надійності за статистичними даними необхідна велика робота щодо правильного та об’єктивного збирання цих даних. Обсяг інформації, яка має бути зібрана, визначається метою оцінки, особливостями апаратури та умовами її експлуатації. Для визначення кількісних показників надійності та виявлення найбільш надійних елементів під час збирання статистичних даних необхідно отримати:
- відомості про блок, вузол, елемент, які відмовили, та їх виробників;
- відомості про час настання відмови;
- відомості про причину відмови;
- відомості про інтенсивність відмов окремих елементів, блоків апаратури в цілому;
- відомості про час ремонту на місці, у майстерні; час простою.
При розрахунку надійності за статистичними даними для кожного типу апаратури складається таблиця потоку відмов. За результатами цієї таблиці будується варіаційний ряд напрацювання даного пристрою. При великій кількості спостережень (декілька сотень) варіаційний ряд перестає бути зручною формою запису статистичного матеріалу. Для додання йому більшої компактності і наочності ряд піддається додатковій обробці.
Для цього весь діапазон зафіксованих значень відмов розподіляється на інтервали часу Δti і підраховується кількість відмов ni, які припадають на кожен і - й інтервал. Отримали статистичний ряд.
За даними статистичного ряду будуються гістограми для оцінки показників надійності. На рис. 1 як приклад наведена гістограма ймовірності безвідмовної роботи апаратури P(t):
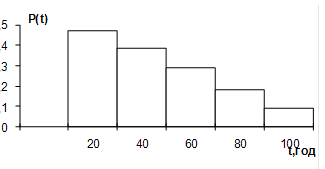
Рисунок 1 – Гістограма ймовірності безвідмовної роботи апаратури
У подальшому побудовані гістограми апроксимуються кривою, за виглядом якої можна орієнтовно встановити закон розподілу відмов шляхом порівняння з відповідними теоретичними кривими. Основною особливістю оцінки надійності за статистичними даними є обмеженість статистичного матеріалу, якого недостатньо для точного визначення експлуатаційних показників.
Слід підкреслити, що будь-яке значення шуканого показника, обчисленого на основі обмеженої кількості дослідів, завжди міститиме елементи випадковості. Таке наближене, випадкове значення показника називають оцінкою показника.
Позначимо оцінку параметра символом ![]() . Щодо оцінки
. Щодо оцінки ![]() параметра v, висувається ряд вимог, яким вона має задовольняти.
параметра v, висувається ряд вимог, яким вона має задовольняти.
По-перше, оцінка ![]() при збільшенні кількості дослідів п має наближатися до параметра v. Оцінка, що має такі властивості, називається обґрунтованою.
при збільшенні кількості дослідів п має наближатися до параметра v. Оцінка, що має такі властивості, називається обґрунтованою.
По-друге, бажано, щоб оцінка ![]() не мала систематичної помилки, тобто, щоб була виконана умова:
не мала систематичної помилки, тобто, щоб була виконана умова:
![]()
Оцінка, яка задовольняє наведеній умові, при якій її математичне сподівання дорівнює параметру, який вона оцінює, називається незсуненою.
По-третє, вибрана незсунена оцінка повинна мати порівняно з іншими оцінками найменшу дисперсію, тобто:
![]()
Оцінка, яка має такі властивості, називається ефективною. На практиці часто потрібно не тільки знайти статистичне математичне сподівання ![]() і дисперсію
і дисперсію ![]() для параметра v, а й оцінити їх точність та надійність. Потрібно знати, до яких помилок може призвести заміна параметра v його точковою оцінкою
для параметра v, а й оцінити їх точність та надійність. Потрібно знати, до яких помилок може призвести заміна параметра v його точковою оцінкою ![]() і з якою мірою впевненості можна очікувати, що ці помилки не вийдуть за певну межу.
і з якою мірою впевненості можна очікувати, що ці помилки не вийдуть за певну межу.
Для характеристики точності та надійності оцінки ![]() користуються так званим довірчим інтервалом і довірчою ймовірністю. Нехай для параметра v отримана з п дослідів незсунена оцінка
користуються так званим довірчим інтервалом і довірчою ймовірністю. Нехай для параметра v отримана з п дослідів незсунена оцінка ![]() . Оцінімо ймовірність, при якій допущена помилка не перевищить деякої величини ε. Позначимо цю ймовірність:
. Оцінімо ймовірність, при якій допущена помилка не перевищить деякої величини ε. Позначимо цю ймовірність:
![]() (8)
(8)
Це є ймовірність того, що справжнє (дійсне) значення v міститиметься в межах ![]()
Ймовірність Р(ε) називається довірчою ймовірністю, межі (границі) ![]() довірчими межами (границями), інтервали Іε=
довірчими межами (границями), інтервали Іε=![]() ±ε – довірчими інтервалами.
±ε – довірчими інтервалами.
Довірчий інтервал характеризує точність отриманого результату, а довірча ймовірність – його надійність.
2.1 Довірчий інтервал при нормальному розподілі
Нехай величина Х розподілена за нормальним законом з параметрами Мх і σх. Розглянемо питання про знаходження довірчих границь для математичного сподівання.
Потрібно знайти ймовірність нерівності:
![]() (9)
(9)
Якби закон розподілу ![]() був відомим, то знаходження ймовірності нерівності (9) не викликало б складнощів. Проте закон розподілу оцінки
був відомим, то знаходження ймовірності нерівності (9) не викликало б складнощів. Проте закон розподілу оцінки ![]() залежить від розподілу величини Х та її невідомих параметрів Мх і σх.
залежить від розподілу величини Х та її невідомих параметрів Мх і σх.
Нам відомо, що величина Х розподілена за нормальним законом, але зважаючи на те, що параметри Мх і σх цього закону невідомі, скористуватися цим законом розподілу неможливо.
Щоб обійти це ускладнення, введемо замість випадкової величини ![]() іншу випадкову величину Тт:
іншу випадкову величину Тт:
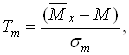 (10)
(10)
де 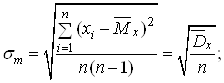 (11)
(11)
п – кількість спостережень;
![]() – статистична дисперсія величини Х.
– статистична дисперсія величини Х.
В математичній статистиці доведено, що випадкова величина Тт підкоряється так званому закону Стьюдента:
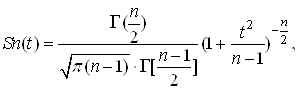 (12)
(12)
де Г(п/2) – гамма – функція;
п – кількість спостережень.
З рівняння (12) видно, що розподіл Стьюдента не залежить від параметрів Мх і σх величини Х, а залежить тільки від аргументу t і кількості спостережень п.
Розподіл Стьюдента дозволяє знайти ймовірність нерівності ![]() Для цього задамося довільним позитивним числом ta і знайдемо ймовірність влучення величини Тт на відрізок (-ta, ta):
Для цього задамося довільним позитивним числом ta і знайдемо ймовірність влучення величини Тт на відрізок (-ta, ta):
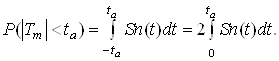 (13)
(13)
Підставимо в ліву частину цієї формули замість Тт його значення з формули (10) і отримаємо:
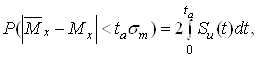 (14)
(14)
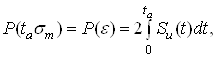 (15)
(15)
де ![]() – довірча ймовірність;
– довірча ймовірність;
![]()
ta – квантиль розподілу Стьюдента для вибраної ймовірності P(ε) та кількості ступенів свободи r=n-1.
Функція ta табульована. За допомогою такої табульованої функції можна вирішувати практичні задачі з оцінки точності математичного спадкування.
Довічний інтервал знаходиться так:
1. Задамося довірчою ймовірністю P(ε). Зазвичай P(ε)=0,9; 0,95; 0,98; 0,99.
2. Знаходимо величину σm за формулою (11).
3. Визначаємо кількість ступенів свободи r=n-1.
За відомими r та P(ε) знаходимо за таблицями (1) величину ta.
5. Помноживши ta на σm, знаходимо ε= ta∙σm – половину довжини довірчого інтервалу.
6. Знаходимо довірчий інтервал ![]()
2.2 Довірчий інтервал при експоненціальному розподілі
При експоненціальному законі розподілу відмов оцінки параметрів λ і напрацювання до відмови То відповідно дорівнюють:
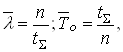 (16)
(16)
де tΣ – сумарне напрацювання;
n – кількість відмов в інтервалі tΣ.
Для неремонтованих елементів сумарне напрацювання:
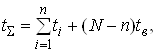 (17)
(17)
де tі – час справної роботи і - го елемента, який відмовив;
N – кількість елементів (приладів);
tв – час випробовувань;
n – кількість елементів (приладів), що відмовили.
Для ремонтованих елементів сумарне напрацювання:
![]() (18)
(18)
Для випадку, коли випробовування проводяться до тих пір, поки не відмовлять всі елементи (прилади), які поставили на випробовування, сумарне напрацювання:
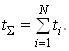 (19)
(19)
Довірчий інтервал для інтенсивності відмов λ за експоненціальним розподілом знаходиться з допомогою квантилів розподілу χ2, в яких параметрами є довірча ймовірність та кількість ступенів свободи r.
Нижня λн і верхня λв границі інтенсивності відмов знаходяться як:
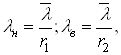 (20)
(20)
де ![]()
![]() . (21)
. (21)
У формулах (21) ![]() квантилі розподілу χ2 при кількості ступенів свободи r=2n.
квантилі розподілу χ2 при кількості ступенів свободи r=2n.
Значення коефіцієнтів r1 і r2 табульовані для різних ймовірностей Р(ε) і кількості елементів, що відмовили n.
Враховуючи, що за експоненціальним розподілом ![]() отримаємо:
отримаємо:
![]()
![]() (22)
(22)
На практиці часто потребується отримати в процесі випробування інтенсивність відмов з помилкою, яка б не перебільшувала задану. В цьому випадку при плануванні випробовувань потрібно визначити кількість відмов п, кількість екземплярів апаратури N, яку поставили на випробовування, сумарне напрацювання апаратури tΣ та довжину етапу випробовувань tв.
Якщо задана гранична помилка виражена у відсотках і дорівнює ξо, то:
![]()
![]()
![]() (23)
(23)
Для експоненціального розподілу часу безвідмовної роботи:
![]()
Тоді, при заданій ймовірності Р(![]() ) і rξ=r1 визначимо кількість відмов п, яку необхідно отримати в процесі випробовувань. Об’єм вибірки за виразом (18). Результати випробовувань вважаються позитивними, якщо:
) і rξ=r1 визначимо кількість відмов п, яку необхідно отримати в процесі випробовувань. Об’єм вибірки за виразом (18). Результати випробовувань вважаються позитивними, якщо:
![]()
![]()
![]() (24)
(24)
2.3 Довірчий інтервал при розподілі Пуассона
надійність електроапаратура експоненціальний
Довірчі границі у випадку розподілу Пуассона обчислюється за формулами :
![]() ;
;![]() (25)
(25)
де а – параметр розподілу Пуассона (математичне сподівання кількості відмов); а = λt;
n – кількість відмов, які виникли в процесі випробовування;
коефіцієнти r1 і r2 визначаються за формулою (21).
Довірчий інтервал для інтенсивності відмов при розподілі Пуассона знаходиться так:
1. Задаємося довірчою ймовірністю Р(ε).
2. За заданими значеннями п та Р(ε) знаходимо коефіцієнти r1 і r2.
3. Розраховуємо за формулою (25) значення ан та ав параметрів розподілу Пуассона.
4. За заданим сумарним напрацюванням tΣ знаходимо довірчі границі для λ:
![]()
![]()
3. Критерії згоди
Між статистичним розподілом та теоретичною кривою на практиці завжди є розбіжності. При цьому потрібно переконатися, викликані ці розбіжності тільки випадковими обставинами, які пов’язані з обмеженою кількістю спостережень, або вони є істотні і пов’язані з тим, що вибрана крива погано вирівнює даний статистичний розподіл. Отже, виникає питання про узгодження теоретичного і статистичного розподілів. Перевірка такої узгодженості здійснюється за критеріями згоди. Критеріями, які найбільш використовуються, є критерій Колмогорова та критерій χ2 Пірсона.
3.1 Критерій Колмогорова
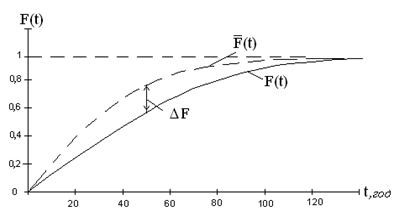
При застосуванні критерію згоди Колмогорова як захід розбіжності між теоретичним і статистичним розподілом розглядається максимальне значення модуля різниці між теоретичною та експоненціальною функціями розподілу.
На рис. 2 наведені теоретична та експоненціальна функції розподілу F(t).
![]()
Рисунок 2 – Функції розподілу F(t)
На підставі цього критерію експериментальний розподіл узгоджується з вибраним теоретичним, якщо виконується умова:
![]() , (26)
, (26)
де ![]() найбільше відхилення теоретичної кривої від експоненціальної;
найбільше відхилення теоретичної кривої від експоненціальної;
п – загальна кількість експоненціальних даних.
Недоліком критерію Колмогорова є те, що він потребує попереднього знання теоретичного розподілу, тобто його можна використовувати тільки тоді, коли відомі не тільки вигляд функції розподілу F(t), її параметри Мt і σt. Такий випадок дуже рідко зустрічається на практиці. Якщо все ж використовувати цей критерій у тих випадках, коли параметри теоретичного розподілу знаходяться за статистичними даними, то критерій дає явно завищені значення, що може привести до невірних висновків.
3.2 Критерій Пірсона χ2
Критерій χ2 Пірсона не потребує побудови самого закону розподілу. Достатньо тільки задатися загальним виглядом функції F(t), а кількісні значення параметрів, які входять до цієї функції, визначаються за даними експерименту.
Припустимо, що виникло п відмов і, отже, маємо ряд напрацювання То1, То2, То3, … Топ пристрою. Потрібно перевірити гіпотезу про те, що статистичний розподіл напрацювання апарата узгоджується з якимось відомим законом.
Розбиваємо вісь часу (від 0 до ∞) на k інтервалів Δt((0,t1), (t1, t2)…(tk-2, tk-1), (tk-1, ∞)). Розраховуємо теоретичну ймовірність Рі потрапляння в і-й інтервал при одному досліді. Підрахуємо кількість пі напрацювання, які попали в і-й інтервал.
Тоді при перевірці такого узгодження з використанням критерію χ2 Пірсона вираховується ймовірність:
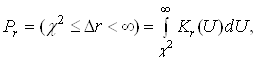 (27)
(27)
де ![]() – міра розбіжності;
– міра розбіжності;
χ2 – функція щільності розподілу, яка розраховується за формулою для всіх k інтервалів:
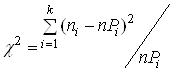 , (28)
, (28)
Де п – загальна кількість відмов; пі – кількість відмов в і- му інтервалі; Рі – ймовірність потрапляння відмов в і-й інтервал; k – кількість інтервалів статистичного ряду.
Функція розбіжності Кr(U) запишеться як:
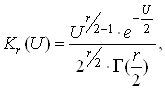 (29)
(29)
де ![]() кількість ступенів свободи розподілу.
кількість ступенів свободи розподілу.
Для розподілу χ2 складені спеціальні таблиці, користуючись якими можна для кожного значення χ2 та кількості ступенів свободи r знайти ймовірність ![]() Якщо ймовірність
Якщо ймовірність ![]() то слід вважати невдалим вибраний теоретичний розподіл. У протилежному випадку вважається, що вибраний теоретичний розподіл узгоджується з експериментальним і може бути прийнятим.
то слід вважати невдалим вибраний теоретичний розподіл. У протилежному випадку вважається, що вибраний теоретичний розподіл узгоджується з експериментальним і може бути прийнятим.
Схема застосування критерію χ2 за оцінкою узгодження теоретичного та статистичного розподілу:
- визначається χ2 за формулою (28);
- знаходиться кількість ступенів свободи ![]()
- за знайденою величиною r та χ2 за таблицями визначаємо ймовірність ![]() ;
;
- якщо ![]() гіпотеза відкидається як неправдоподібна, при
гіпотеза відкидається як неправдоподібна, при ![]() гіпотезу можна визнати такою, яка не суперечлива дослідним даним.
гіпотезу можна визнати такою, яка не суперечлива дослідним даним.
4. Контроль надійності
Контроль надійності має своєю метою перевірити гіпотезу про те, що надійність не нижче встановленого рівня. При цьому кінцевим результатом, як правило, є одне з двох рішень: прийняти партію, вважаючи надійність апаратури задовільною, або забракувати контрольовану партію апаратури як ненадійну. Оскільки контроль надійності проводиться на основі випробовувань визначеної вибірки, то під час прийняття рішення можливі два види помилок:
- помилка першого роду – коли добра партія бракується;
- помилка другого роду – коли погана партія приймається.
Ймовірність помилки першого роду називається ризиком виробника, позначимо її літерою α .
Ймовірність помилки другого роду називається ризиком споживача, позначимо її літерою β.
Існують три основних методи контролю надійності:
- метод одноразової вибірки (одинокий контроль);
- метод дворазової вибірки (подвійний контроль);
- метод послідовного аналізу.
Кожен з цих методів має свої переваги і недоліки та може бути використаний у тому або іншому конкретному випадку. Найбільше розповсюдження в практиці контролю надійності отримали одинокий та метод послідовного аналізу. Це пояснюється тим, що метод подвійного контролю потребує більшого часу контролю та більш складних розрахунків. Цей метод ми розглядатимемо.
Найбільш економічним методом контролю надійності є послідовний. Метод послідовного контролю надійності застосовується на стадіях технічного проекту або робочої конструкторської документації дослідного зразка виробу. А тому при випробовуванні дослідного зразка апаратури перевага надається методу послідовного аналізу. Метод же одноразової вибірки використовується під час випробовування серійних зразків.
Сукупність умов випробовування контрольних апаратів і правил прийняття рішень називається планом контролю.
Під сукупністю умов випробування розуміються умови бракування і приймання, задані значення α та β, обсяг випробовувань тощо. Правила прийняття рішень визначаються методами контролю.
4.1 Метод одноразової вибірки
Метод одноразової вибірки полягає в тому, що з контрольної партії обсягу No виробів береться одна випадкова вибірка обсягу N екземплярів. Потім виходячи з вибраних No, N, α або β, встановлюється оціночний норматив no. При контролі кількості дефектних апаратів партія визначається надійною, якщо кількість дефектних апаратів ( кількість відмов) nk менше або дорівнює no, тобто:
![]() (30)
(30)
де no – оціночний норматив.
Якщо nk >no,то партія вибраковується. Якщо контролювати середнє напрацювання на відмову ![]() (контроль щодо напрацювання), то необхідно так встановити сумарний час випробовувань tΣ (сумарне напрацювання виробів на вибірки N) та оціночний норматив Тк, щоб забезпечувати задані ризики α і β.
(контроль щодо напрацювання), то необхідно так встановити сумарний час випробовувань tΣ (сумарне напрацювання виробів на вибірки N) та оціночний норматив Тк, щоб забезпечувати задані ризики α і β.
Оціночний норматив встановлюється таким чином, що при:
![]() (31)
(31)
результати випробовувань оцінюються як задовільні, а при:
![]() (32)
(32)
результати випробовувань оцінюються як незадовільні (партія бракується).
Тривалість етапу випробовувань tв при обраному обсязі вибірки N буде:
![]() (33)
(33)
У подальшому розглядатимемо тільки контроль щодо напрацювання.
Позначимо ймовірність відмови апаратури за час tв, за який вона визначається надійною, через q1, а ймовірність відмови, при якій апаратура бракується, через q2.
Середнє напрацювання на відмову надійної партії позначимо через То1, а ненадійної партії – через То2. Крім того, введемо позначення:
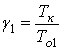 і
і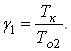 (34)
(34)
Для контролю надійності методом одноразової вибірки під час виконання умов N≤0,1No і q1≤0,1 можна користуватися розподілом Пуассона, тоді:
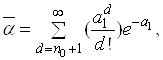 (35)
(35)
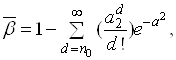 (36)
(36)
де ![]() – ризик виробника, близький до заданого α;
– ризик виробника, близький до заданого α;
![]() ризик споживача, близький до за даного β.
ризик споживача, близький до за даного β.
![]()
![]()
![]() (37)
(37)
Знайдемо співвідношення:
![]() (38)
(38)
Для контролю надійності, основаного на розподілі Пуассон. За допомогою цих таблиць за заданими N, α, β, То1 і То2 можна визначити тривалість tв, значення α1 і γ1, оціночні нормативи no і Tk. При цьому можна визначити обсяг вибірки N, якщо задані α, β, q1 і q2.
В таблицях немає значення α2 і γ2, але при α=β їх можна визначити з виразів:
![]()
![]()
4.2 Метод послідовного аналізу
Послідовний метод контролю не передбачає попереднього обсягу вибірки. Інформація про надійність апаратів, які випробовуються, накопичується при послідовному, зростаючому обсязі випробовувань. Послідовний контроль надійності за напрацюванням здійснюється у відповідності з правилами:
- партія приймається, якщо сумарний час випробувань:
![]() (39)
(39)
- партія бракується, якщо :
![]() (40)
(40)
- випробування продовжуються, якщо:
![]() (41)
(41)
де nk – кількість відмов у робочих точках графіка послідовного контролю напрацювання;
tk – час контролю k – ї точки;
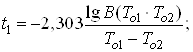 (42)
(42)
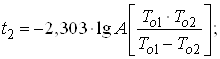 (43)
(43)
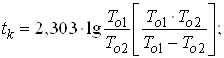 (44)
(44)
![]()
![]() (45)
(45)
To1 – напрацювання на відмову надійної партії;
To2 – напрацювання на відмову ненадійної партії.
Наведемо графік контролю за методом послідовного аналізу (рис. 3).
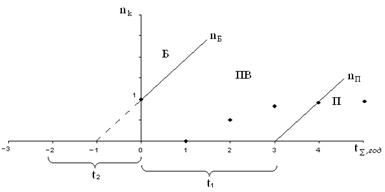
1. Зона Б – приймається рішення про бракування партії;
2. Зона ПВ – приймається рішення про продовження вимірювання;
3. Зона П – приймається рішення про приймання партії.
Рисунок 3 – Графік послідовного аналізу
Робочими точками графіка є:
![]() Перша
Перша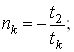
![]()
Друга![]()
![]() (46)
(46)
Третя![]()
![]()
Якщо α=β, то ![]() тобто ризик виробника дорівнює ризику споживача, то і час однаковий.
тобто ризик виробника дорівнює ризику споживача, то і час однаковий.
Прямі nБ і nП поділяють площину на три зони:
- зона Б – приймається рішення про бракування партії;
- зона ПВ – приймається рішення про продовження вимірювання;
- зона П – приймається рішення про приймання партії.
З рівнянь (39) і (40) видно, що прямі nБ і nП завжди паралельні, оскільки їх кутові коефіцієнти однакові і дорівнюють nk tk.
Для контролю за методом послідовного аналізу необхідно на побудованому графіку відкладати дослідні точки, отримані у процесі випробовувань. Коли дослідні точки мають вийти з зони продовження випробовувань (ПВ), випробовування закінчується. На рис. 3 точками зображений випадок, коли випробовування закінчились прийманням партії апаратури.
Наведемо алгоритм дії методу послідовного аналізу.
1. При заданих значеннях α, β, То1 і То2 знаходимо коефіцієнти А і В.
2. За формулами (42), (43) та (44) знаходимо час напрацювання t1, t2 і tk.
3. За формулами (39) і (40) знаходимо сумарний час напрацювання апаратури.
Складемо таблицю значень nk, tΣпр і tΣбр.
Таблиця 1 – Значення сумарного часу випробувань
nk | 0 | 1 | 2 | 3 | 4 | - - | k |
tΣпр | - - | ||||||
tΣбр | - - |
5. Будуємо графік за допомогою цієї таблиці з урахуванням формули (46).
- 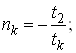
![]()
- ![]()
![]()
- ![]()
![]()
6. Ухвалюємо рішення про приймання або бракування партії апаратури.
5. Випробовування за оцінкою надійності
Підвищення якості, комфортних характеристик і функціональних можливостей побутової ЕА, яка розробляється, призводить до зростання її складності, отже, до збільшення вимог щодо надійності апаратури. Висока надійність побутової ЕА є одним з основних показників її якості.
Вимоги до надійності побутової ЕА викладені в технічних умовах (ТУ). Нормованим показником безвідмовності є напрацювання на відмову То. Випробовуванням на надійність підлягають апарати дослідної партії, установчих серій і серійного виробництва. Випробовування на надійність приладів дослідної партії (зразків) проводить підприємство-розробник за участю заводу-виробника.
У табл. 2, 3 і 4 наведені вимоги щодо безвідмовності різних видів ПЕА згідно з ГОСТ – 21317 – 87.
Таблиця 2 – Вимоги щодо безвідмовності телевізорів
| Вид телевізора | Напрацювання на відмову То, год | |
| Стаціонарних | Переносних | |
| Телевізори кольорового зображення | 10200 | 8000 |
| Телевізори чорно-білого зображення | 11250 | 8650 |
Таблиця 3 – Вимоги щодо безвідмовності магнітофонів
| Вид магнітофона | Напрацювання на відмову То, год при групі складності | |
| 0 і 1 | 2; 3 і 4 | |
| Магнітофони | 5000 | 4200 |
| Відеомагнітофони | 5000 |
|
Таблиця 4 – Вимоги щодо безвідмовності радіоприймачів
| Вид радіоприймача | Напрацювання на відмову То, год при групі складності | |||
| 0 | 1 | 2 | 3; 4 | |
| Стаціонарний | 11000 | 9150 | 5500 | 4500 |
| Переносний | 9150 | 9150 | 5500 | 4500 |
| Автомобільний | 7800 | Подобное:
Copyright © https://referat-web.com/. All Rights Reserved | ||
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

