Скачать

Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)

Предложенная мне тема «Решение задачи об оптимальной интерполяции с помощью дискретного преобразования Фурье (ДПФ)» написана на основе книги В. Н. Малоземова и С. М. Машарского «Основы дискретного гармонического анализа». Дискретный гармонический анализ – это математическая дисциплина, результаты которой активно используются в цифровой обработке сигналов. По ходу изучения книги возникли новые задачи, две из которых приведены в разделе «Решения задач». В данной работе также сравнивается ДПФ с непрерывным преобразованием Фурье. В приложениях в случае классического преобразования приходится приближенно заменят интегралы некоторыми суммами. При этом основная трудность связана с необходимостью оценки погрешности на каждом из последующих этапов. ДПФ тем выгоднее и отличаются, что здесь с самого начала вместо интегралов имеем дело с суммами. При этом основные цели использования ДПФ также достигаются.

Рассматриваются различные преобразования - периодических векторов, среди которых центральную роль играет ДПФ. Задача об оптимальной интерполяции является приложением ДПФ.

Отдельные задачи в рамках дипломной работы мне решить не удалось. Они не вошли в дипломную работу.

Основная работа свелась к изложению основных фактов с подробными доказательствами. В начале дипломной работы имеется раздел «Вспомогательный материал», в котором кратко изложены факты, необходимые для чтения основного текста. Эти факты хорошо известны и касаются тех понятий и терминов, которые встречаются в теории чисел, в теории линейных комплексных пространств и в линейной алгебре. Все эти понятия используются для получения более важных результатов в последующих параграфах.

Далее вводится пространство - периодических векторов  и устанавливается тот факт, что - линейное комплексное пространство.

Над элементами этого пространства определяются прямое и обратное ДПФ.

Решены задачи, составлена и апробирована программа, которая реализует оптимальную интерполяцию. Также составлены программы, которые вычисляют свертку двух периодических векторов и ДПФ.

При решении задачи оптимальной интерполяции сначала переходим к новым переменным с помощью ДПФ. Далее полеченную задачу решаем методом множителей Лагранжа. И, наконец, переходим к исходным переменным с помощью формулы обращения.

2

§ 1. Вспомогательный материал

В данной работе используются следующие обозначения:

Z, R, C – множества целых, действительных и комплексных чисел соответственно;

m : n – множество последовательных целых чисел {m, m+1, … , n}.

1.Корни из единицы. Допустим – натуральное число, . Введём комплексное число

 (1)

По формуле Муавра при натуральном k получаем

 (2)

В частности,  Число  называется корнем – й степени из единицы.

Формула (2) верна при k=0. Покажем, что она верна и при целых отрицательных степенях . Действительно,

Значит, получили, что формула (2) справедлива при всех

Отметим, что  и  при натуральном . Из (2) и свойств тригонометрических функций следует также, что при всех целых  и

Применяя формулу Эйлера, имеем

2.Комплексное унитарное пространство. Будем говорить, что в комплексном линейном пространстве определено скалярное умножение, если всякой паре векторов a, b поставлено в соответствие число, обозначаемое символом (a, b) и называемое скалярным произведением векторов a и b. Причём (a, b) будет, вообще говоря, комплексным числом.

3

При этом должны выполнятся аксиомы:

1., где черта обозначает, как обычно, переход к сопряжённому комплексному числу;

2.

3.

4.Если а ≠ 0, то скалярный квадрат вектора а строго положителен, т.е.

(а. а) > 0, а если (а, а) = 0, то а = 0.

Комплексное линейное пространство называется унитарным пространством, если в нём задано скалярное умножение.

Векторы а и b называются ортогональными, если их скалярное произведение равно нулю

(а, b) = 0.

Система векторов называется ортогональной системой, если все векторы этой системы попарно ортогональны.

Назовём вектор b нормированным, если его скалярный квадрат равен единице

(b, b) = 1.

При этом, если  - ортонормированная база и векторы а, b

имеют в этом базе записи

а = , , то .

Также имеем равенство

 (3)

3.Вычеты. Пусть и  – натуральное число. Существует единственное целое число , такое, что

 (4)

Оно называется целой частью дроби  и обозначается

Разность  называется вычетом  по модулю  и обозначается .

4

Нетрудно показать, что

. (5)

Действительно, умножим неравенства (4) на  и вычтем .

Получим , что равносильно (5).

4.Функции комплексного переменного. На плоскостях комплексных переменных z и w рассмотрим соответственно множества  и .

Если указан закон f, по котором каждому значению  сопоставляется единственное значение , то говорят, что на множестве Е определена однозначная функция комплексного переменного z и пишут w=f(z).

Функции определяются как суммы степенных рядов:

, , . (6)

Из этих равенств непосредственно можно получить следующие формулы Эйлера:

, , . (7)

5.Матрицы. Прямоугольная таблица чисел, записанная в виде

 (8)

называется матрицей.

Коротко матрицу обозначают так: , ;

где  - элемент данной матрицы, который находится в i-й строке и j-м столбце матрицы А.

5

Некоторые свойства матриц:

1. сумма С = А + В двух матриц А и В одного размера mn – это матрица

С = (с), где с = a + b для всех i, j;

сумма матриц разных размеров не определяется.

2.Произведение С = λА матрицы А и элемента λС – это матрица того же размера, что и А, причём при всех i, j.

3.Произведение С = АВ матрицы А размера mn и матрицы В размера np – это матрица С размера mp такая, что

Произведение матриц в общем случае некоммутативно, т.е АВ≠ВА.

Транспонированная матрица  (по отношению к матрице А) – такая матрица, что .

Совокупность элементов  квадратной матрицы  называется главной диагональю матрицы.

Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны 0, называется единичной матрицей и обозначается буквой Е.

Напомним, что

АЕ = А и ЕА = А.

Матрица называется ортогональной, если строки образуют ортогональную систему векторов и норма каждой строки равна единице.

Квадратная матрица называется симметрической, если

.

6.Определители. Всякое расположение чисел 1, 2, …, n в некотором определённом порядке называется перестановкой из n чисел.

Говорят, что в данной перестановке числа i и j составляют инверсию, если i>j, но i стоит в этой перестановке раньше j.

Перестановку называют чётной, если её символы составляют чётное число инверсий, и нечётной – в противоположном случае.

Всякое взаимно однозначное отображение А множества первых n натуральных чисел на себя называется подстановкой n-й степени, причём, очевидно, всякая подстановка А может быть записана при помощи двух перестановок, подписанных одна под другой.

6

Подстановка А будет чётной, если общее число инверсий в двух строках любой её записи чётно, и нечётной – в противоположном случае.

Определителем n-го порядка называется алгебраическая сумма n! членов, составленная следующим образом: членами служат всевозможные произведения n элементов матрицы, взятых по одному в каждой строке и в каждом столбце, причём член берётся со знаком плюс, если его индексы составляют чётную подстановку и со знаком минус в противоположном случае.

Для определителя квадратной матрицы А используется обозначение |A| или detA.

Свойства определителя:

1.определитель транспонированной матрицы равен определителю исходной, т.е.

det(AT) = detA;

2.если все элементы строки умножить на , то определитель умножится на ;

3. если каждый элемент некоторой строки определителя представлен в виде суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей, у которых все строки, кроме данной прежние, а в данной строке в первом определителе стоят первые, а во втором – вторые слагаемые;

3’. аналогичные свойства для столбцов;

4. если две какие–либо строки (столбца) матрицы поменять местами, то определитель матрицы умножиться на (-1);

5. определитель с двумя одинаковыми строками (столбцами) равен 0;

6. определитель не изменится, если к какой–либо его строке (столбцу) прибавить другую строку (столбец), умноженную на .

Алгебраическое дополнение  к элементу квадратной матрицы определяется равенством

,

где  (минор) – определитель матрицы, полученной удалением из А – й строки и – го столбца.

7

Определитель можно разложить по любой строке и любому столбцу.

Разложение по i–й строке имеет вид:

.

7.Обратная матрица. Матрица А, у которой detA≠0, называется невырожденной.

Обратная матрица В = А-1 (по отношению к матрице А) – такая матрица, что АВ = ВА = Е.

Обратная матрица существует в том и только в том случае, когда матрица А невырожденная.

В этом случае

, (9)

где – алгебраические дополнения к элементам .

Если матрица А – ортогональная и симметрическая, то

А-1 = А.

8.Конечные разности. Конечные разности вектора  определяются рекуррентно :

Вместо  пишут обычно .

Конечную разность  порядка  можно непосредственно выразить через значения вектора .

Справедлива формула

. (10)

8

§ 2. Пространство N – периодических комплекснозначных векторов

Зафиксируем натуральное число N. Определяем пространство следующим образом

.

Введём в  две операции – операция сложения двух векторов и операция умножения вектора на комплексное число:

В результате получим линейное комплексное пространство.

Введём символ , у которого, когда  делится на , и при остальных  Очевидно, что

Лемма 1. Для  справедливо следующее равенство

 (1)

Доказательство. Так как в обеих частях (1) стоят N–периодические векторы, проверим равенство при Поскольку при  выполняются неравенства

то  при  Отсюда имеем

Таким образом, лемма доказана.

Формула (1) даёт аналитическое представление вектора х по его значениям на основном периоде

9

Рассмотрим следующую систему сдвигов вектора

 (2)

Покажем, что эта система линейно независима на Z. Действительно, пусть

 при

Как отмечалось, левая часть этого равенства равна  так что  при всех

Поэтому согласно лемме 1 любой вектор х разлагается по линейно независимой системе (2). Таким образом, показали, что система (2) является базисом пространства . При этом размерность пространства  равна N, т.е.

Следующее вспомогательное утверждение будем часто использовать в дальнейшем.

Лемма 2. Для любого вектора  при всех  справедливо равенство

 (3)

Доказательство. Пусть  где  - целая часть дроби, а - остаток от деления  на . Воспользуемся  периодичностью вектора  и тем, что  Тогда получим

Что и требовалось доказать.

10

Следствие. В условиях леммы 2 справедливо равенство

 (4)

Действительно,

Следствие доказано.

Определим в  скалярное произведение и норму

Как и в комплексном унитарном пространстве, в  два вектора x, y называются ортогональными, если  Вектор называется нормированным, если ||x||=1.

Лемма 3. При всех  справедливо равенство

 (5)

Доказательство. Зафиксируем k и введём вектор  После чего, учитывая чётность  и формулу (1), запишем

Что и требовалось доказать.

Следствие. Система векторов (2) является ортонормированной, т. е. образует ортонормированный базис в пространстве

11

Наряду с вектором  будем рассматривать векторы , . Эти

векторы определяются следующим образом, а именно получаем векторы со значениями

 соответственно.

Отметим также, что

Введём понятия чётности и нечётности вектора.

Вектор  называется чётным, если  и нечётным, если  при всех .

Вектор  называется вещественным, если , и чисто мнимым, если

12

§ 3. ДПФ. Основные свойства

Возьмём корень  степени из единицы

Лемма 1. Имеет место равенство

,  (1)

Доказательство. Заметим, что в левой части (1) стоит  – периодическая функция.

На самом деле,

 при

–периодическим является и  Поэтому достаточно проверить равенство (1) при .

При  оно тривиально. Пусть  Из формулы для суммы членов геометрической прогрессии имеем

 при

Положив , получим

 при .

Равенство доказано.

1.Непрерывное преобразование Фурье и формула обращения.

Функция , заданная на всей числовой прямой и определяемая формулой

, (2)

называется преобразованием Фурье исходной функции .

13

Формула, выражающая  через её преобразование Фурье и имеющая вид

, (3)

называется формулой обращения для непрерывного преобразования Фурье.

Следует обратить внимание на сходство между формулами (1) и (2).

Вторая из них отличается от первой лишь знаком в показателе и множителем  перед интегралом.

2.Дискретное преобразование Фурье (ДПФ). Определение.

ДПФ – это отображение

,

сопоставляющее вектору  вектор  со значениями

 (4)

Вектор X называется спектром Фурье вектора x или просто спектром, а величины X(k) – компонентами спектра или спектральными составляющими соответствующего вектора.

Теорема 1. Имеет место формула обращения

 (5)

Доказательство. Из формул (1), (4) и из формулы (1) предыдущего параграфа имеем

Теорема доказана.

14

Формулу (5) можно записать компактно так:

Введём обозначение . Тогда формула (5) для ДПФ примет вид

 (6)

Из равенства (6) видно, что вектор  разлагается по системе векторов

 (7)

Коэффициентами в этом разложении являются компоненты спектра.

Лемма 2. Для любого целого k имеем .

Доказательство. Действительно,

Лемма доказана.

Лемма 3. Система векторов (7) ортогональна. При этом  при всех

Доказательство. Имеем при

Отсюда очевидным образом следует требуемое.

15

Лемма 4. Система  линейно независима.

Доказательство. Чтобы показать линейную независимость данной системы, надо проверить равенство

тогда и только тогда, когда

Возьмём скалярное произведение и покажем справедливость данного равенства:

Т.к. векторы ортогональные, то

 при

Нетрудно видеть, что . Так как , то

Лемма доказана.

Установлено, что система (7) образует ортогональный базис в пространстве Этот базис называется экспоненциальным.

Возьмём вектор

Тогда

 - разложение вектора  в базисе (7).

Умножив обе части данного разложения на , получим

Учитывая тот факт, что , приходим к равенству

 (9)

Таким образом, формула (9) определяет коэффициенты Фурье вектора

16

Рассмотрим матрицу, элементами которой является компоненты векторов :

,

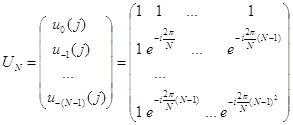Это матрица ДПФ. Очевидно, у этой матрицы строки ортогональны.

Введем некоторые свойства данной матрицы и получим матрицу обратного преобразования.

Лемма 5. Матрица  будет ортогональной.

Доказательство. Для того чтобы доказать факт надо показать:

1.строки данной матрицы образуют ортогональную систему векторов;

2.норма каждой строки равна единице.

Покажем сначала первое, т.е.

Далее

Лемма доказана.

17

Лемма 6. Матрица  является симметрической.

Доказательство. Чтобы доказать данную лемму, покажем справедливость равенства

Итак,

,

Лемма доказана.

Раз матрица  - ортогональная и симметрическая, то

Тогда  т.к.

Итак, - матрица обратного преобразования Фурье.

В дальнейшем нам понадобится следующее утверждение.

Лемма 7. Если имеем действительное евклидовое пространство, то

. (10)

В случае комплексного пространства имеем

. (11)

Доказательство.

Пусть  - матрица преобразования Фурье.

Тогда

.

18

Рассмотрим скалярное произведение

- левая часть нашего

равенства.

Учитывая, что

рассмотрим

 - правая часть

нашего равенства.

Правая часть равенства совпала с левой частью, значит, (11) - верное равенство.

Лемма доказана.

Далее рассмотрим свойства ДПФ.

Теорема 2. Пусть Тогда

 (12)

Доказательство. Учитывая формулу (12) и тот факт, что матрица  является симметрической и ортогональной, получим

Что и требовалось доказать.

Следствие. В условиях теоремы 2 справедливо равенство

 (13)

Формула (13) называется равенством Парсеваля, а формула (12) – обобщённым равенством Парсеваля.

19

§ 4. Задача восстановления координат

Ставится задача следующим образом. Пусть  где  и

Также считается известными и

Требуется узнать, можно ли найти  при условии, что

В приводимой ниже теореме показывается, что при некотором предположении координаты вектора  полностью восстанавливаются.

Теорема. Если спектр  вектора  равен нулю на некотором множестве , то

 (1)

Доказательство. По формуле обращения для ДПФ, учитывая условию теоремы, приходим к следующему равенству

 (2)

Зафиксируем  и пусть  Продолжив  периодически с периодом  на , получим вектор , принадлежащий  Вычислим его ДПФ:

Применяя формулу обращения, приходим к равенству

20

Подставив это выражение в (2), придём к (1). Действительно,

Теорема доказана.

Упростим формулу для h. Очевидно, что

Так как

.

Аналогичным образом получаем

.

При  имеем

Итак, получаем

 (3)

21

В простейшем случае, когда  формула (3) принимает вид

 (4)

Проверим это. При всех  имеем

что равносильно требуемому.

В случае  нашу теорему можно переформулировать так: если на основном периоде  половина значений спектра  с индексами  равна нулю, то вектор  восстанавливается по половине своих

компонентов  с помощью формулы

где h имеет вид (4).

22

§5.Интерполяционная задача.

Рассмотрим следующую интерполяционную задачу

 (1)

В этой задаче требуется построить вектор , который в узлах  принимает заданные значения . Также известно, что старшие коэффициенты Фурье равны нулю.

Решение данной интерполяционной задачи сформулируем в виде теоремы.

Теорема. Решением задачи (1) является вектор

 (2)

Доказательство. Однородная система

согласно формуле (1) из предыдущего параграфа имеет только нулевое решение. Таким образом, задача (1) однозначно разрешима при любых комплексных  Рассмотрим решение  этой задачи. Аргумент  представим в виде  В силу определения  и формулы (1) предыдущего параграфа, получим

Теорема доказана.

23

§ 6. Свёртка векторов

Свёрткой векторов  называется вектор  с компонентами

 (1)

Теорема 1 (о свёртке). Пусть  Тогда

 (2)

где справа стоит покомпонентное произведение спектров§, которое определяется следующим образом

Доказательство.

По формуле (2) из § 2 имеем

что соответствует (2). Что требовалось доказать.

Из теоремы 1 как следствие можно получить следующий результат.

Следствие. Справедливо равенство

 (3)

Сформулируем свойства свёртки в виде теоремы.

Теорема 2. Свёртка коммутативна и ассоциативна.

Доказательство. Коммутативность , непосредственно следует из (3). Проверим ассоциативность. Возьмём три вектора  и обозначим через  их спектры.

24

Учитывая (2) и (3), получаем

Теорема доказана.

Преобразование  называется линейным, если для любых  и любых , имеет место равенство

В качестве примера линейного преобразования рассмотрим оператор сдвига , сопоставляющий вектору  вектор  с координатами

Преобразование  называется стационарным, если

для всех

Из определения получаем

,

где - тождественный оператор.

Теорема 3. Преобразование  будет линейным и стационарным тогда и только тогда, когда найдётся вектор , такой, что

 при всех  (4)

Доказательство.

Необходимость. Учитывая, что  перепишем формулу (1) из § 2 в виде

Так как оператор  линейный и стационарный, то получим

25

Допустив, что , приходим к равенству

Достаточность. Линейность сверточного оператора очевидна. Остается проверить стационарность. В силу коммутативности свертки

Далее запишем

Что и требовалось доказать.

Рассмотрим операцию взятия конечной разности  порядка:

Сначала покажем, что  где

Согласно (1) из § 2 имеем

что и требовалось установить.

26

§ 7. Решение задачи оптимальной интерполяции

Допустим, что - натуральное число. Рассмотрим следующую экстремальную задачу:

 (1)

В этой задаче требуется построить возможно более гладкий вектор, принимающий в узлах  заданные значения  а гладкость данного вектора характеризуется квадратом нормы конечной разности r – го порядка. Чаще всего рассматривается случай, когда r=2.

Проведём замену переменных

После чего перепишем задачу (1) в компонентах  Этот процесс начнём с целевой функции. Как было показано в последнем примере предыдущего параграфа  где  определяется соответственно формулой (5) того же параграфа. Далее используя равенство Парсеваля и формулу из теоремы о свёртке, получаем

Отметим только, что здесь

Введём обозначение

27

Тогда  и

 (2)

Теперь обратимся к ограничениям. Имеем

Таким образом, ограничения задачи (1) принимают вид

Последняя формула представляет собой разложение вектора  по экспоненциальному базису. Она равносильна тому, что

 (3)

где  На основании (2) и (3) приходим к эквивалентной постановке задачи (1):

 (4)

Последняя задача, т.е. задача (4) распадается на m независимых подзадач, соответствующих разным

 (5)

28

Поскольку , то при  приходим к задаче

Решение этой задачи имеет вид

 (6)

Заметим только, что минимальное решение целевой функции равно нулю.

Допустим теперь, что

В этом случае мы данную задачу решаем методом множителей Лагранжа.

Строим функцию Лагранжа:

.

Итак,

 (7)

Чтобы найти  воспользуемся ограничениями

.

Из этого выражения находим :

Подставив  в (7), получим решение задачи (4) при

29

Введём обозначение

Тогда окончательное решение запишется в виде

 (8)

Формулы (6) и (8) определяют  на всём основном периоде  По формуле обращения находим единственное решение задачи (1):

 (9)

При этом минимальное значение целевой функции задачи (1) складывается из минимальных значений целевых функций задач (5) при , так, что

.

Преобразуем (9) к более удобному для вы