Радиолокационные установки
1. Основные способы распространения радиоволн
1.1 Отражение от поверхности земли (двухлучевая модель)
1.2 Прохождение плоской электромагнитной волны через плоский слой диэлектрика
1.3 Дифракция радиоволн
1.3.1 Геометрия зон Френеля
1.3.2 Модель дифракции радиоволн на одиночном клине
1.3.3 Дифракция на нескольких клиньях
1.4 Рассеяние радиоволн
2. Практические модели, используемые для расчета ослабления сигнала в радиоканалах
2.1 Потери передачи в удаленных линиях
2.2 Модели радиолиний вне зданий
2.2.1 Метод Okumura
2.2.2 Модель Hata
2.2.3 Уточнение метода Hata
3. Программа расчета напряженности электромагнитного поля с учетом затенения зданиями
3.1 Расчет напряженности в точке приема методом интегрирования
4. Экономическое обоснование дипломной работы
4.1 Введение
4.2 Экономическое обоснование работы
4.3 Расчет материальных затрат
4.4 Расчет основной заработной платы
4.5 Расчет дополнительной заработной платы
4.6 Затраты на социальные выплаты
4.7 Затраты на электроэнергию
4.8 Амортизационные отчисления
4.9 Накладные расходы
4.10 Калькуляция затрат
4.11 Выводы
5. Безопасность и экологичность проекта
5.1 Краткая характеристика работы
5.2 Безопасность работы
5.2.1 Электробезопасность
5.2.2 Пожарная безопасность
5.2.3 Микроклимат на рабочем месте
5.2.4 Освещенность на рабочем месте
4.2.4.1 Расчет необходимой освещенности
4.2.4.2 Расчет искусственной освещенности
5.2.5 Шум и вибрации
5.3 Эргономичность проекта
5.3.1 Эргономические требования к рабочему месту
5.3.2 Оценка качества программы
5.4.1 Ионизационное излучение
5.4.2 Электромагнитное излучение
5.4.3 Статическое электричество
5.5 Чрезвычайные ситуации
5.6 Вывод о безопасности и экологичности работы
Перечень сокращений, условных обозначений, символов, единиц и терминов
ВДТ - видео дисплейный терминал
ИС - интегральная схема
КЕО - коэффициент естественной освещенности
ЛВЖ - легковоспламеняющаяся жидкость
ОВЧ - очень высокие частоты
ПО - программное обеспечение
РЭА - радиоэлектронная аппаратура
СНиП -
УВЧ - ультравысокие частоты
(П) ЭВМ - (персональная) электронно-вычислительная машина
ЭМИ - электромагнитное излучение
Введение
Путь радиоволны от передатчика к приемнику в системах связи УКВ - диапазона крайне разнообразен: от их прямой видимости до сильно закрытого препятствиями, домами, деревьями пути. В отличие от проводной связи, где параметры постоянны, в беспроводной связи радиоканалы имеют существенно случайные параметры, часто сложно анализируемые. Моделирование радиолинии - наиболее сложная задача проектирования радиосистем. Оно в основном выполняется статистически с использованием данных экспериментов, выполненных порой именно для такой же или аналогичной системы.
Механизм распространения радиоволн в системах связи различен, но в основном может быть представлен отражением, дифракцией и рассеянием. Большинство систем работают в городах, где нет прямой видимости антенн передатчика и приемника, а наличие высоких зданий вызывает большие дифракционные потери. Благодаря многократным переотражениям от различных объектов, радиоволны проходят различный путь. Интерференция этих волн вызывает сильное изменение уровня сигнала от положения приемника.
Моделирование распространения радиоволн основано на предсказании среднего уровня принимаемого сигнала на заданном расстоянии от излучателя, а также в определении разброса его значений в зависимости от конкретной ситуации на трассе. Расчет радиолинии позволяет определить зону обслуживания передатчика. Моделирование среднего уровня сигнала в зависимости от расстояния между передатчиком и приемником называется крупномасштабным моделированием, поскольку позволяет определить сигнал на большом удалении (несколько сотен и тысяч метров).
С другой стороны, модели характеризуют быстроменяющиеся значения уровня принимаемого сигнала на малых смещениях (несколько длин волн) или за короткое время (секунды) - они называются мелкомасштабными моделями.
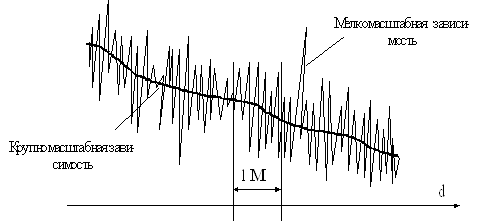
Рис.1.1 Изменение напряженности поля в зависимости от расстояния до передающей антенны с учетом влияния случайных факторов на частоте 1800 МГц
При перемещении мобильного приемника на малые расстояния принимаемый сигнал может меняться очень сильно. Это происходит из-за того, что принимаемый сигнал представляет собой сумму многих волн, приходящих с различных направлений, проходящих разное расстояние и имеющих различную амплитуду и фазу. Суммарный сигнал подчиняется закону Релея. В зависимости от трассы радиоканала мелкомасштабная девиация может меняться на 3-4 порядка, т.е. уровень сигнала может меняться на 30-40 дБ (рис.1.1). Если мобильный приемник будет достаточно далеко, средний уровень сигнала убывает.
1. Основные способы распространения радиоволн
Три основных способа распространения радиоволн:
Отражение - имеет место при падении волны на объекты с размерами много больше длины волны. Наблюдаются, например, отражения от земли, стен зданий и т.п.
Дифракция - явление возникновения вторичных волн при падении радиоволны на препятствие с острыми кромками. Дифракцией обусловлено наличие поля за препятствиями в зоне геометрической тени. На высоких частотах дифракция, как и отражение, существенно зависит от геометрии объекта, а также амплитуды, фазы и поляризации поля.
Рассеяние - имеет место при распространении волны в среде с мелкими объектами (меньше длины волны).
1.1 Отражение от поверхности земли (двухлучевая модель)
В задачах мобильной связи прямое распространение радиоволн между передающей и приемной антеннами встречается достаточно редко, поэтому модель распространения волн в свободном пространстве имеет ограниченное применение. Полезная для практики двухлучевая модель распространения волн (рис.5) основана на законах геометрической оптики.
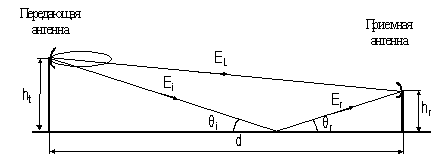
Рис.1.1 Прямой и отраженный лучи в точке приема радиоволн
Суммарное поле в точке приема обусловлено влиянием прямого и отраженного от земной поверхности лучей:
![]() .
.
Из рис.1.1 видно, что разность хода прямого луча и луча с отражением от земли
![]() . (1.1)
. (1.1)
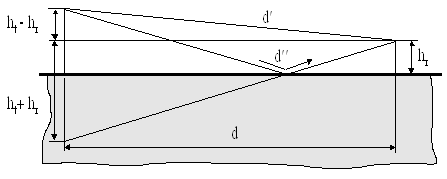
Рис.1.2 Мнимый излучатель поля
Если расстояние ![]() , то (1.1) может быть упрощено с помощью разложения Тейлора:
, то (1.1) может быть упрощено с помощью разложения Тейлора:
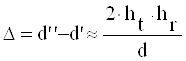 , м. (1.2)
, м. (1.2)
Тогда разность фаз прямого и отраженного лучей
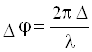 . (1.3)
. (1.3)
Суммарное электрическое поле в точке приема прямого и отраженного лучей при сделанных допущениях вычисляется по формуле
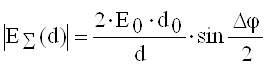 ,
, ![]() , (1.4)
, (1.4)
где Е0 - напряженность поля, создаваемая излучающей антенной на некотором опорном расстоянии d0 в свободном пространстве (без учета отражения), ![]() .
.
На больших удалениях, когда выполняется соотношение
![]() ,
,
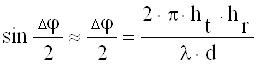 . (1.5)
. (1.5)
Суммарное поле в этом случае может быть аппроксимировано выражением
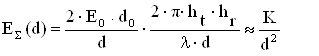 ,
,![]() , (1.6)
, (1.6)
где К - константа, связанная с амплитудой поля Е0, высотами подвеса антенн и длиной волны. Мощность, принятая приемной антенной, пропорциональна квадрату напряженность поля:
![]() . (1.7)
. (1.7)
Из формулы (1.7) видно, что на больших расстояниях принятая мощность убывает обратно пропорционально d4 или 40 дБ на декаду. Это существенно быстрее, чем в свободном пространстве.
Для двухлучевой модели в соответствии с (1.7) потери мощности в радиоканале определяются выражением
![]() , дБ. (1.8)
, дБ. (1.8)
1.2 Прохождение плоской электромагнитной волны через плоский слой диэлектрика
Пусть плоская волна падает нормально на границу I плоского слоя диэлектрика (рисунок 1.3, а). Часть энергии волны отразится от границы I и будет распространяться в обратном направлении, а часть проникнет сквозь границу I и будет распространяться в прямом направлении до границы II. Здесь будет наблюдаться аналогичная картина: часть энергии проникнет сквозь границу II, а другая часть отразится от этой границы и будет распространяться к границе I и т.д.

Рис.1.3 Волны вблизи диэлектрического слоя:
а - нормальное падение волны, б - косое падение волны.
Введем следующие обозначения: A - волна, падающая на слой диэлектрика; B - волна, движущаяся от границы I влево (сумма первичной отраженной волны и всех волн, проникающих через границу I справа); C - волна, движущаяся в слое слева направо (сумма первичной проникающей через границу I волны и всех волн, отраженных от этой границы внутрь слоя); D - волна, движущаяся в слое справа налево (сумма всех волн, отраженных от границы II); F - волна, прошедшая сквозь границу II (сумма всех волн, проникших через эту границу).
Величины A, B, C, D, F выражают комплексные значения амплитуд электрических векторов соответствующих волн.
Радиопрозрачность слоя характеризуется двумя величинами:
коэффициентом отражения
![]() (1.9)
(1.9)
и коэффициентом прохождения
![]() . (1.10)
. (1.10)
Оба коэффициента так же, как и напряженности A, B, F, являются, вообще говоря, комплексными.
Учитывая непрерывность касательных составляющих электрического и магнитного полей на границах сред воздух - диэлектрик, можно выразить комплексные амплитуды отраженной (B) и прошедшей сквозь слой (F) волн через комплексную амплитуду падающей волны (A) и затем с помощью соотношений (1.9) и (1.10) получить формулы для расчета коэффициентов R и T.
Если волна падает на слой под косым углом, то отраженную волну и волну, прошедшую сквозь слой, находят путем суммирования волн всех “порядков" B1, B2, …, а также соответственно F1, F2, … (рисунок 1.3, б).
Расчетные формулы для коэффициентов R и T имеют вид (22)
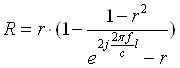 (1.11)
(1.11)
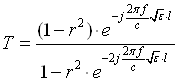 , (1.12)
, (1.12)
где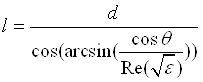 . (1.13)
. (1.13)
Здесь d - толщина слоя; f- частота; с = 3*108 - скорость света в вакууме; r - коэффициент отражения на границе сред воздух - диэлектрик.
Коэффициент отражения для поля вертикальной поляризации
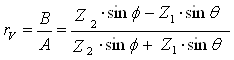 . (1.14)
. (1.14)
Коэффициент отражения для поля горизонтальной поляризации
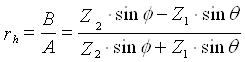
![]() , (1.15)
, (1.15)
где Zi - характеристическое сопротивление 1-й или 2-й среды.
![]() . (1.16)
. (1.16)
Если первая среда - свободное пространство (e1=1), а вторая среда не обладает магнитными свойствами (m1 = m0), то выражения (1.14), (1.15) упрощаются:
![]()
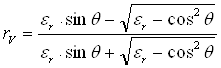 , (1.17)
, (1.17)
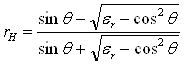 . (1.18)
. (1.18)
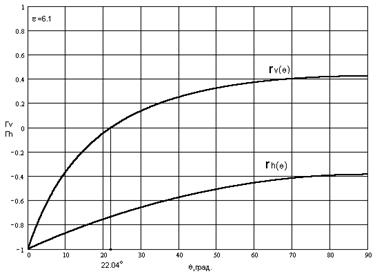
Рис.1.4 Зависимость коэффициента отражения волны вертикальной и горизонтальной поляризации от угла падения ![]() , падающей на бетонную поверхность (er = 6.1)
, падающей на бетонную поверхность (er = 6.1)
Для углов падения, близких к скользящим ![]() , коэффициенты отражения
, коэффициенты отражения ![]() ;
; ![]() .
.
Для некоторого угла ![]() коэффициент отражения для волны вертикальной поляризации
коэффициент отражения для волны вертикальной поляризации ![]() . Этот угол называется углом Брюстера qБР (угол, для которого нет отраженной волны вертикальной поляризации):
. Этот угол называется углом Брюстера qБР (угол, для которого нет отраженной волны вертикальной поляризации):
 . (1.19)
. (1.19)
Если первая среда - воздух, а диэлектрическая проницаемость второй среды er, то
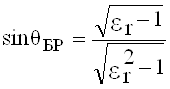 . (1.20)
. (1.20)
Угол Брюстера имеет место только для вертикальной поляризации поля. Коэффициент прохождения слоя можно представить в виде
![]() . (1.21)
. (1.21)
Если из аргумента Фсл вычесть запаздывание по фазе Ф0, существовавшее на отрезке, равном толщине слоя до его размещения на пути волны, то получим дополнительный сдвиг по фазе, вносимый слоем,
![]() , (1.22)
, (1.22)
Где
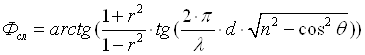 , (1.23)
, (1.23)
![]() .
.
Таким образом, диэлектрический слой влияет не только на амплитуду проходящей сквозь него волны, но и на фазу. (21)
1.3 Дифракция радиоволн
Явление дифракции позволяет радиоволнам распространяться вокруг сферической земной поверхности за горизонт и за различные препятствия. Несмотря на перекрытие прямой видимости и существенное уменьшение уровня сигнала, он все таки остается достаточным для приема.
Феномен дифракции объясняется принципом Гюйгенса - вторичного переизлучения точек фронта волны с различной фазой (зон Френеля). Напряженность поля определяется векторной суммой вклада вторичных излучателей.
1.3.1 Геометрия зон Френеля
Пусть между излучателем и приемником расположено препятствие - экран высотой h бесконечных размеров в поперечном сечении. Расстояние от экрана до излучателя - d1, до приемника - d2.
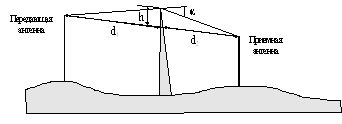
Рис.1.5 Дифракция радиоволн на клиновидном препятствии
Ясно, что путь через кромку препятствия больше прямого. Полагая, что h<
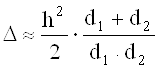 . (1.27)
. (1.27)
Соответствующая ему разность фаз
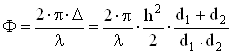 , (1.28)
, (1.28)
где используется приближение для малого аргумента tg x » x, а угол a аппроксимирован выражением
 .
.
Выражение (1.28) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля - Кирхгофа:
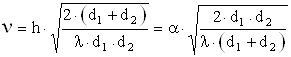 , (1.29)
, (1.29)
где a подставляется в радианах, все остальные параметры - в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения
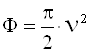 . (1.30)
. (1.30)
Из выражения (1.30) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.
Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nl/2 по сравнению с прямым лучом (l - длина волны, n - целое число).
В мобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.

Рис.1.6 Формирование зон Френеля
Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.
1.3.2 Модель дифракции радиоволн на одиночном клине
Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.
Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.

Рис.1.7 Варианты перекрытия видимости антенн препятствием
Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением
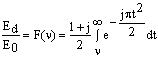 , (1.31)
, (1.31)
где Е0 - напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F (n) - комплексный интеграл Френеля. Значение интеграла F (n) определяется из графиков и таблиц.
Коэффициент дифракционного усиления с препятствием (обычно он меньше 1) по сравнению со свободным пространством
![]() , дБ. (1.32)
, дБ. (1.32)
График этой функции показан на рис.1.8
Gd, дБn
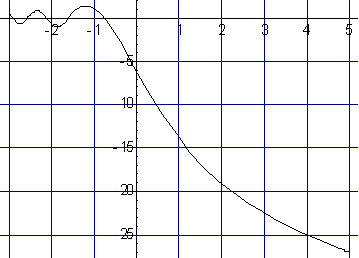
Рис.1.8 Зависимость коэффициента дифракционного усиления от значения параметра дифракции n
Приближенно можно считать:
![]() (1.33a)
(1.33a)
![]() (1.33б)
(1.33б)
![]() (1.33в)
(1.33в)
![]() (1.33г)
(1.33г)
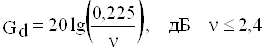 (1.33д)
(1.33д)
1.3.3 Дифракция на нескольких клиньях
Если на пути между излучателем и приемником имеется несколько препятствий, то все они аппроксимируются одним эквивалентным препятствием (рис.1.9).
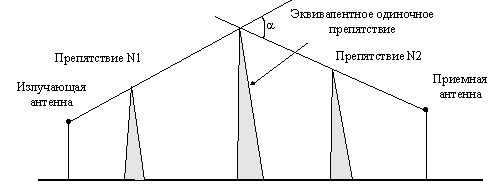
Рис.1.9 Эквивалентное клиновидное препятствие в задаче связи с двумя препятствиями
Эта модель хорошо работает для двух препятствий, для нескольких - возникают определенные математические трудности.
1.4 Рассеяние радиоволн
Потери от рассеяния радиоволн на препятствиях обычно много меньше потерь отражения и дифракции. Это объясняется тем, что рассеяние волн происходит во всех направлениях (на таких объектах, как мачты, лампы, деревья и т.д.).
Плоские поверхности с размерами много больше длины волны могут моделироваться как отражающие поверхности. Однако наличие неровностей изменяет отражение. Неровность поверхности определяется критерием Релея, который определяет критическую высоту hcнеровностей при падении волны под углом qi:
![]() . (1.34)
. (1.34)
Поверхность считается гладкой, если разброс минимальных и максимальных высот меньше hc. Для неровных поверхностей коэффициент отражения r умножается на коэффициент потерь рассеяния ps.
Полагая, что высота неровностей h распределена случайным образом с гауссовым законом распределения, коэффициент потерь рассеяния
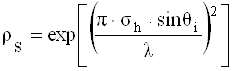 , (1.35)
, (1.35)
где sh - стандартная девиация высоты поверхности вокруг среднего значения высоты. После некоторых уточнений коэффициент потерь рассеяния с хорошим совпадением с практикой определяется выражением
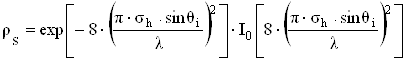 , (1.36)
, (1.36)
где I0 - функция Бесселя первого рода нулевого порядка. Коэффициент отражения электромагнитного поля для неровностей h>hc определяется выражением
![]() . (1.37)
. (1.37)
Степень рассеяния радиоволн от препятствий больших размеров, например, крупных домов, может характеризоваться поперечником рассеяния. Поперечник рассеяния объекта (RCS) определяется как отношение плотности потока мощности рассеянного поля в направлении приемника к плотности потока мощности, падающей на рассеивающий объект, и имеет размерность м2. Анализ основан на геометрической теории дифракции и физической оптике и может быть использован для задач расчета поля, рассеянного большими зданиями. Для городских условий используется бистатическое уравнение излучения, описывающее распространение волны в свободном пространстве и поле, рассеянное между объектами и затем переизлученное в направлении приемника.
![]()
![]() , (1.38)
, (1.38)
где dt иdr - расстояние от рассеивающего объекта до излучателя и приемника. Это уравнение корректно для дальней зоны излучателя и приемника.
2. Практические модели, используемые для расчета ослабления сигнала в радиоканалах
Большинство моделей, используемых при решении задач распространения радиоволн, учитывают одновременно аналитические и экспериментальные данные. Экспериментальный подход основан на использовании графиков и аналитических выражений, описывающих данные предварительных измерений.
Преимущество этого подхода состоит в учете большинства факторов, влияющих на распространение радиоволн. Иногда в задачах мобильной связи используются классические модели радиолиний, которые позволяют моделировать в крупном масштабе линии связи. Например, двухлучевая модель позволила предсказать работоспособность сотовых систем до их появления. Ниже представлены некоторые модели радиолиний.
2.1 Потери передачи в удаленных линиях
Как теоретические, так и экспериментальные исследования подтвердили, что принимаемая мощность изменяется по логарифмическому закону.
Этот закон выполняется как для радиолиний вне зданий, так и внутри их.
Средние крупномасштабные потери при произвольном расстоянии излучатель - приемник описываются выражением
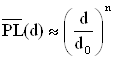 (2.1)
(2.1)
или в логарифмическом масштабе
![]() , дБ, (2.2)
, дБ, (2.2)
где n - показатель степени, который показывает, с какой скоростью возрастают потери передачи от расстояния; d0 - расстояние от излучателя до границы отсчета, d - расстояние между излучателем и приемником. Черта в (2.1), (2.2) означает среднее из возможных значений потерь для данного расстояния d. На диаграмме в логарифмическом масштабе график ослабления описывается наклонной прямой с коэффициентом наклона 10. n дБ на декаду. Показатель n зависит от конкретных параметров среды распространения.
Таблица. Показатель n ослабления поля для различных условий распространения радиоволн
| Среда | Показатель n |
| Свободное пространство | 2 |
| Сотовая связь в городе | 2.7 - 3.5 |
| Сотовая связь в городе в тени | 3 - 5 |
| В зданиях при прямой видимости | 1.6 - 1.8 |
| Препятствия, загромождения в зданиях | 4 - 6 |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Радиопередающие устройства
Министерство образования Республики КомиГосударственное образовательное учреждение«Воркутинский техникум сервиса и торговли»Конт
- Радиоприемное устройство для приема сигналов типа F3EH
- Радиоприемные устройства
Теория РПУ формируется под воздействием, с одной стороны, общих разделов радиоэлектроники, с другой — прикладных отраслей, определяющи
- Радиоприемные устройства
Радиоприемные устройства входят в состав радиотехнических систем связи, т.е. систем передачи информации с помощью электромагнитных в
- Радиочастотная идентификационная метка на поверхностных акустических волнах
Ежегодный рост мирового товарооборота и масштабное увеличение числа грузоперевозок привело к созданию систем регистрации и идентифик
- Радиоэлектронные каналы утечки информации
- Радиоэлектронные средства навигации и связи
Copyright © https://referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

