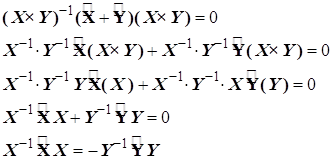Пространственное движение одной частицы
О математическом описании многомерных систем
Конфигурационное пространство
Ознакомившись со свойствами волновых функций и уровней одномерных стационарных систем, мы сделали лишь первый шаг к оформлению математических основ теории химической связи. Далее предстоит рассмотрение стационарных пространственных движений одной частицы. Такие модели реалистичнее передают черты физических явлений, но это связано с усложнением математического аппарата.
При переходе к описанию пространственного движения частицы число координат возрастает до трёх, т.е. конфигурационное пространство переменных в этом случае – обычное трёхмерное пространство, соответствующее трём степеням свободы. Геометрические образы волновых функций подобны образам полей, распределенным в объёме. Если же система содержит не одну, а две частицы, то независимых пространственных координат уже шесть, конфигурационное пространство шестимерно. Не следует считать, что это какая-то исключительная ситуация: атом водорода содержит два частицы – ядро и электрон, и эта система полностью описывается с помощью 6 координат. При переходе к N-частичной системе размерность конфигурационного пространства соответственно увеличивается до ЗN.
Геометрическая наглядность при анализе волновых функций таких многомерных систем недостижима. Поэтому для химии особенно важны такие модели, которые допускают построение наглядных графических образов. Этому условию отвечает пространственное движение одной частица.
4.1.2. Дифференциальные уравнения в частных производных и метод разделения переменных
4.1.2.1. Многие фундаментальные теоретические модели физики построены с использованием математического аппарата теории дифференциальных уравнений в частных производных. Напомним читателю, что само понятие частной производной восходит к стремлению изучить поведение многомерной функции при изменении лишь одной из независимых переменных без затрагивания прочих. Сложная многомерная проблема как бы разделяется на набор одномерных задач, которые по отдельности намного легче поддаются анализу. Позволим себе сравнить ситуацию с многоголосием в музыкальном произведении: каждая одноголосная партия проста, и её может воспроизвести даже нёискушенный исполнитель, но полифония требует уже изрядной подготовки.
4.1.2.2. Уравнение Шредингера относится к числу дифференциальных уравнений в частных производных второго порядка. В принципе оно должно включать все координаты каждой из частиц в качестве аргументов, т.е. соответствующее конфигурационное пространство 3N–мерно. Сложность решения уравнения Шредингера возрастает с увеличением числа переменных, поэтому необходимы физически обоснованные способы упрощения задач такого рода. К счастью, существует очень простой и эффективный прием, называемый методом разделения переменных, который предложен Фурье. Обсудим кратко основы этого метода.
4.1.2.3. Для простоты рассмотрим всего две независимые переменные 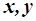 и определим в таком конфигурационном пространстве, во-первых, некоторую функцию F или семейство функций и, во-вторых, некоторый линейный оператор
и определим в таком конфигурационном пространстве, во-первых, некоторую функцию F или семейство функций и, во-вторых, некоторый линейный оператор 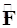 . Этот оператор может содержать в качестве слагаемых и сами переменные, и функции от них, например,
. Этот оператор может содержать в качестве слагаемых и сами переменные, и функции от них, например, 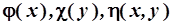 , и операторы частного дифференцирования первого порядка
, и операторы частного дифференцирования первого порядка 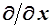 и
и 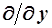 , и второго порядка, включая перекрёстное дифференцирование, т.е.
, и второго порядка, включая перекрёстное дифференцирование, т.е. 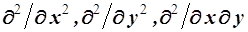 . Вообще говоря, можно и не ограничиваться вторым порядком дифференцирования, но для наших задач его достаточно. Перед производными в качестве коэффициентов могут быть также функции от переменных х и у. Так что дифференциальное уравнение для семейства функций представится в виде
. Вообще говоря, можно и не ограничиваться вторым порядком дифференцирования, но для наших задач его достаточно. Перед производными в качестве коэффициентов могут быть также функции от переменных х и у. Так что дифференциальное уравнение для семейства функций представится в виде
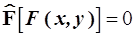 . (4. I)
. (4. I)
4.1.2.4. В самом простом случае для разделения переменных в уравнении (4.1) необходимо, чтобы оператор 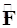 допускал группировку всех выражений и действий над каждой из переменных в отдельные слагаемые, например
допускал группировку всех выражений и действий над каждой из переменных в отдельные слагаемые, например 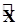 и
и 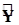 . Вводимые нами символы операторов красноречиво указывают на преобразуемые ими переменные и не требуют дополнительных пояснения. Итак, оператор
. Вводимые нами символы операторов красноречиво указывают на преобразуемые ими переменные и не требуют дополнительных пояснения. Итак, оператор 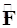 должен быть представлен в аддитивной форме
должен быть представлен в аддитивной форме
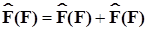 (4.2)
(4.2)
Для разделения переменных в дифференциальном уравнении (4.1) искомую функцию F(x,y) следует представить в виде произведения двух сомножителей X(x) и Y(у), каждый из которых является неизвестной функцией лишь одного аргумента:
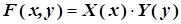 , (4.3)
, (4.3)
или 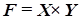
4.1.2.5. Аддитивный характер оператора и мультипликативная структура функции позволяет разделить переменные в дифференциальном уравнении (4.1). Подставив в него (4.2) и (4.3), получим
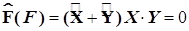 (4.4)
(4.4)
Дальнейшая процедура состоит в следующем:
слева умножаем выражение (4.4) на 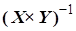 ;
;
преобразуем дифференциальное уравнение (4.4), учитывая, что операторы 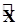 и
и 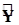 не затрагивают чужую переменную и не изменяют функции от неё;
не затрагивают чужую переменную и не изменяют функции от неё;
производим сокращения и
разделяем переменные.
или 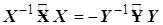 (4.5)
(4.5)
4.1.2.6. В силу независимости аргументов функций X и Y, а также и преобразований над ними, выражение (4.5) следует приравнять постоянной величине, а именно
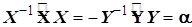 (4.6)
(4.6)
Цепочка равенств (4.6) – это не что иное, как система двух дифференциальных уравнений, связанных между собой лишь постоянной 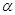 , которая в каждой конкретной задаче находится из дополнительных математических или физических условий. Систему можно записать так
, которая в каждой конкретной задаче находится из дополнительных математических или физических условий. Систему можно записать так
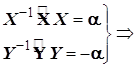
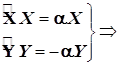
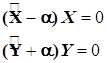 (4.7)
(4.7)
Каждое из дифференциальных уравнений системы (4.7) включает лишь одну переменную и решается самостоятельно.
4.1.2.7. Такая схема легко распространяется на конфигурационное пространство 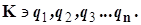 В таком случае общее выражение для дифференциального уравнения (4.1) выглядит следующим образом
В таком случае общее выражение для дифференциального уравнения (4.1) выглядит следующим образом
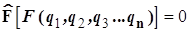 . (4.8)
. (4.8)
4.1.2.8. Одномерные операторы–слагаемые 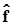 , на которые разлагается многомерный оператор
, на которые разлагается многомерный оператор 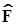 , с одной стороны, построены на разных переменных,
, с одной стороны, построены на разных переменных, 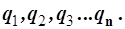 а с другой стороны, могут иметь разную конструкцию, хотя это и не обязательно. Последнее их отличие отметим ниже индексами a,b,c... Основное условие возможности разделения переменных выражается формулой, определяющей аддитивную структуру оператора
а с другой стороны, могут иметь разную конструкцию, хотя это и не обязательно. Последнее их отличие отметим ниже индексами a,b,c... Основное условие возможности разделения переменных выражается формулой, определяющей аддитивную структуру оператора
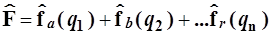 (4.9)
(4.9)
4.1.2.9. Аддитивность оператора (4.9) порождает мультипликативность решения уравнения (4.8), т.е.
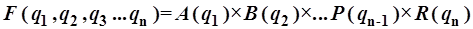 (4.10)
(4.10)
Подставляя (4.9) и (4.10 ) в (4.8), получаем
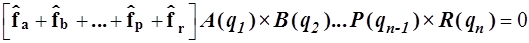 (4.11)
(4.11)
Каждый из одномерных операторов дифференцирования преобразует лишь ту функцию-сомножитель которая содержит его же аргумент. Остальные функции-сомножители без нарушения равносильности уравнения (4.11) можно вынести влево за такой оператор:
4.1.2.10 соответствии с методом Фурье, слева домножаем выражение на 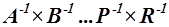 и получаем
и получаем
Отделяя любое из слагаемых, например, первое, вводим первую из констант 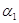 связывающих отдельные компоненты решения
связывающих отдельные компоненты решения
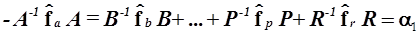
 и т.д.
и т.д.
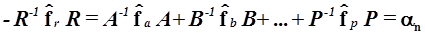 (4.12)
(4.12)
4.1.2.11. Суммируя левые части уравнений системы (4.12) и все константы в правой части, получаем
т.е.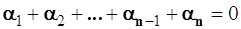 или
или 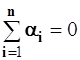 (4.13)
(4.13)
Таким образом, параметры отдельных одномерных дифференциальных уравнений оказываются связанными между собой равенством (4.13).
4.1.2.12.При разделении переменных многомерного дифференциального уравнения можно их предварительно группировать. В таком случае в выражениях (4.8 ) – (4.10)под каждым из символов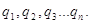 может подразумеваться целый набор переменных. Именно таким образом производится анализ движения в системе многих частиц. Вначале очень сложное и громоздкое исходное уравнение всегда претерпевает подготовительное преобразование, состоящее в том, что производится выделение отдельных уравнений, относящихся к индивидуальным частицам.
может подразумеваться целый набор переменных. Именно таким образом производится анализ движения в системе многих частиц. Вначале очень сложное и громоздкое исходное уравнение всегда претерпевает подготовительное преобразование, состоящее в том, что производится выделение отдельных уравнений, относящихся к индивидуальным частицам.
4.1.2.13. Встречаются ситуации, когда, на первый взгляд, разделить переменные невозможно, так как оператор 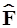 содержит сложные функции, включающие все эти переменные либо часть из них. В таких случаях часто к цели ведёт замена переменных, например, переход от декартовых координат х, у к полярным или к комбинации исходных декартовых. Преобразования, связанные со сменой координат, и в классической и в квантовой механике являются самым обычным делом. Выбор подходящей системы переменных часто подсказывает выражение потенциальной энергии
содержит сложные функции, включающие все эти переменные либо часть из них. В таких случаях часто к цели ведёт замена переменных, например, переход от декартовых координат х, у к полярным или к комбинации исходных декартовых. Преобразования, связанные со сменой координат, и в классической и в квантовой механике являются самым обычным делом. Выбор подходящей системы переменных часто подсказывает выражение потенциальной энергии 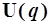 . Ниже мы встретимся с такими примерами.
. Ниже мы встретимся с такими примерами.
4.1.2.14. Следует отметить, что простая аддитивная форма оператора 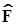 не является непременным условием разделения переменных в дифференциальном уравнении (4.8). Встречаются и более сложные конструкции операторов, допускающие возможность использования основных принципов решения дифференциальных уравнений в частных производных по методу Фурье с разделением переменных. Ниже мы столкнемся с такими случаями.
не является непременным условием разделения переменных в дифференциальном уравнении (4.8). Встречаются и более сложные конструкции операторов, допускающие возможность использования основных принципов решения дифференциальных уравнений в частных производных по методу Фурье с разделением переменных. Ниже мы столкнемся с такими случаями.
Различным комбинациям квантовых чисел ![]() может отвечать одно и то же значение суммы квадратов
может отвечать одно и то же значение суммы квадратов ![]() В этом случае все такие состояния относятся к одному вырожденному уровню. Обозначим их число – кратность вырождения уровня – буквой g. На примере шести низших уровней кубического "ящика" проследим их вырождение . Для этого, как обычно, составим таблицу состояний и уровней (табл. 4. 1.) и изобразим энергетическую диаграмму этой системы ( рис. 4.1.).
В этом случае все такие состояния относятся к одному вырожденному уровню. Обозначим их число – кратность вырождения уровня – буквой g. На примере шести низших уровней кубического "ящика" проследим их вырождение . Для этого, как обычно, составим таблицу состояний и уровней (табл. 4. 1.) и изобразим энергетическую диаграмму этой системы ( рис. 4.1.).
Квантовые числа состояний ( | Энергетические уровни
| Кратность вырождения уровня g |
| 1,1,1 | 3 | 1 |
1,1,2 1,2,1 2,1,1 | 6 | 3 |
1,2,2 2,1,2 2,2,1 | 9 | 3 |
1,1,3 1,3,1 3,1,1 | 11 | 3 |
| 2,2,2 | 12 | 1 |
1,2,3 1,3,2 2,1,3 3,1,2 2,3,1 3,2,1 | 14 | 6 |
Вырождение энергетических уровней кубического “ящика" связано с его высокой пространственной симметрией. Сжатие или удлинение куба вдоль какого-либо направления (при этом параметр a принимает разные значения ) поникает симметрию системы и приводит к снятию вырождения уровней. Следует указать, что такая закономерность является универсальной: чем выше симметрия системы, тем больше кратность вырождения её уровней. При понижении симметрии происходит расщепление ранее вырожденных уровней.
Как у всякой функции трёх переменных, у волновой функции пространственной системы передать графически можно лишь отдельные свойства, тогда, как её полный графический образ практически недоступен.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Ректификационная установка непрерывного действия для разделения смеси: ацетон - изопропиловый спирт - вода
- РН-метрия
Оглавление.Введение. 4Глава 1. Основы метода потенциометрического титрования. 51.1. Понятие потенциометрического титрования; 51.2. Виды поте
- Синтез и свойства амилнитрита
- Синтез изоамилового эфира уксусной кислоты реакцией этерификации (гидролиза) сложных эфиров
- Синтез изобутилового эфира уксусной кислоты реакцией этерификации
- Синтез метанола
Синтез метанола из оксида углерода и водорода1. Технологические свойства метанола Метанол (метиловый спирт) СН3ОН представляет бесцветн
- Синтез нитробензойной кислоты
Исторически большинство исследований в области химии порфиринов были направлены на изучение, синтез и определение биохимических свойс
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.