Проектирование многопустотной железобетонной плиты перекрытия
1. РАЗБИВКА БАЛОЧНОЙ КЛЕТКИ И ВЫБОР ОПТИМАЛЬНОГО ВАРИАНТА
1.1 Исходные данные для проектирования
Здание больницы шестиэтажное с неполным железобетонным каркасом с кирпичными стенами. Расстояние в свету между стенами 18x21,4 м. Высота этажа 3,6 м. Нормативная нагрузка 3,8 кН/м2, в том числе длительная нагрузка 1,8 кН/м2 (1, прил. 1). Коэффициент надежности по нагрузке γf=1,3 (2, п. 3.7). Коэффициент надежности по назначению здания γп =1,0 (1, прил. 6). Плиты многопустотные с круглыми пустотами.
Таблица 1 – Характеристики элементов
| Сборная плита | Ригель | Колонна | Фундамент | |
| Класс бетона | В25 | В20 | В25 | В20 |
| Класс арматуры | АIV | AIII | AIII | AIII |
1.2 Варианты разбивки балочной клетки
Первый вариант – балки расположены вдоль помещения (рис. 1.1). Характеристики варианта: плиты 6,00х1,20 – 10 шт., 6,00х1,50 – 14шт., 6,30х1,20 – 5 шт., 6,30х1,50 – 7шт.; связевые плиты 6,00х2,20 – 4 шт., 6,3х2,2 – 2 шт.; пролет балок (по осям колонн) 7,40 м.
Второй вариант – балки расположены поперек помещения (рис. 1.2). Характеристики варианта: плиты 5,40х1,20 – 32 шт., 5,40х1,50 – 4шт., 5,40х2,20 – 4 шт.; связевые плиты 5,40х2,20 – 8 шт.; пролеты балок (по осям колонн) 5,4 м.
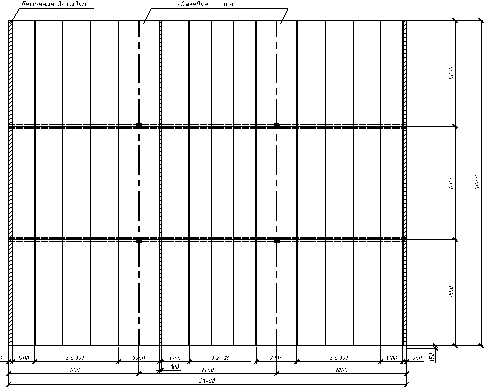
Рисунок 1.1. Расположение балок вдоль помещения
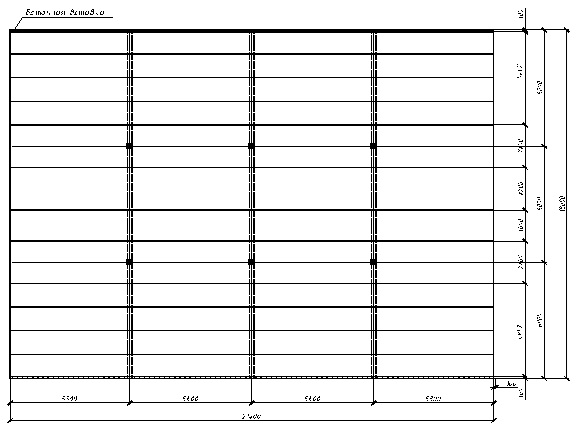
Рис.1.2. - Расположение балок поперек помещения
1.3 Расчет вариантов
Для сравнения вариантов по расходу железобетона, необходимо определить требуемые размеры балок перекрытия в обоих вариантах при одинаковом коэффициенте армирования. Экономическое значение этого коэффициента для балок равно μэ = 1,2 – 1,8 %.
1.3.1 Сбор нагрузок на 1 м2 перекрытия
Нормативную нагрузку от собственного веса пола принимаем по (1, прил. 2): керамический пол – 1,2 кН/м2. Собственный вес плиты принимаем по (1, прил. 3): плита с круглыми пустотами - 2,5 кН/м2. Сбор нагрузки на 1 м2 перекрытия представлен в табличной форме (табл. 1.1).
Таблица 1.1 - Сбор нагрузок на перекрытие
| Нагрузка | Нормативная нагрузка, кН/м2 | γf | Расчетная Нагрузка, кН/м2 |
| Постоянная | |||
| Керамическая плитка | 0,3 | 1,1 | 0,33 |
Слой цементного раствора 0,03х22кН/м3 | 0,66 | 1,3 | 0,85 |
| Звукоизоляция | 0,24 | 1,2 | 0,28 |
| Многопустотная плита с круглыми пустотами | 2,5 | 1,1 | 2,75 |
Итого γn=1 | 3.70 | 4,21 | |
| Временная | 3.8 | 1,2 | 4.56 |
| в том числе длительная | 1.8 | 1.2 | 2.16 |
| кратковременная | 2.0 | 1,2 | 2.4 |
| Полная | 7.5 | 8.77 | |
| в том числе постоянная и длительная | 5.5 | - | |
| кратковременная | 2.0 | – |
1.3.2 Расчет первого варианта
Назначение предварительных размеров балки. Высота:
![]()
![]() 7,4м=0,925…0,616 м.
7,4м=0,925…0,616 м.
Принимаем h = 0,7 м. Ширина:
![]() м.
м.
Принимаем b = 0,3 м.
Собственный вес 1 погонного метра балки равен:
Qb = b h γ = 0,3 x 0,70 x 25 = 5,25кН/м,
где γ =25 кН/м3 – удельный вес бетона.
Расчетная нагрузка на погонный метр балки (рис. 1.3) равна:
![]() 8,77+5,25х1,1= 59,05 кН/м.
8,77+5,25х1,1= 59,05 кН/м.
Рис. 1.3 - Нагрузка на погонный метр балки.
Момент в первом пролёте:
![]()
во втором пролете:
![]()
Принимаем μэ = 1,5 %. Тогда:
![]()
где ![]() МПа (3, табл. 22);
МПа (3, табл. 22); ![]() МПа (3, табл. 13); γb2=0,9 (3, табл. 15)
МПа (3, табл. 13); γb2=0,9 (3, табл. 15)
Определяем значение h0:
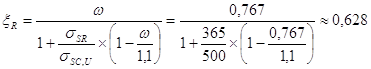 (3, формула (25))
(3, формула (25))
где ![]() (2, формула (26))
(2, формула (26))
Так как ![]() (0,528 < 0,628), то
(0,528 < 0,628), то
![]() ;
;
![]() =0,47 м.
=0,47 м.
и h = h0 + a = 0,47+0,055=0,525 м. Принимаем h = 0,55 м.
1.3.3 Расчет второго варианта
Оставим как и в первом варианте, предварительные размеры балки 0,3х0,70м. Тогда:
Расчетная нагрузка на погонный метр балки равна:
![]() 8,77+5,25х1,1=52,69 кН/м.
8,77+5,25х1,1=52,69 кН/м.
Момент в пролёте:
![]() ;
;
Принимая μэ = 1,5 %, имеем:
![]() ,
, ![]() ,
, ![]() ;
;
![]() =0,38 м.
=0,38 м.
h=h0+a=0,38+0,055=0,435 м. Принимаем h = 0,45 м.
1.4 Сравнение вариантов
Поскольку расход железобетона на плиты остается постоянным для обоих вариантов (перекрывается одинаковая площадь), сравнение производится по расходу железобетона на балки и колонны (пределах этажа). Размер сечения колонны принимается 0,25 м.
Данные по сравнению вариантов сведены в таблицу 1.2.
№ вар-та | Наименование деталей | Кол-во штук | Сечение м2 | Длина м | Расход железобетона, м3 |
| 1 | Балки крайние | 4 | 0,3 х 0,55 | 7 | 4,62 |
| Балки средние | 2 | 0,3 х 0,55 | 7,4 | 2,442 | |
| Колонны | 4 | 0,3 х 0,3 | 3,60 | 0,9 | |
| Плиты | 42 | – | – | – | |
| Итого | – | – | – | 7,962 | |
| 2 | Балки крайние | 6 | 0,3 х 0,45 | 6 | 4,86 |
| Балки средние | 3 | 0,3 х 0,45 | 6 | 2,43 | |
| Колонны | 6 | 0,3 х 0,3 | 3,6 | 1,35 | |
| Плиты | 48 | – | – | – | |
| Итого | – | – | 8,38 | ||
Таблица 1.2 - Сравнение вариантов
Вывод: По расходу железобетона и количеству деталей принимаем 1-й вариант.
2 РАСЧЕТ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПЛИТЫ С КРУГЛЫМИ ПУСТОТАМИ
2.1 Исходные данные, характеристики материалов и технология изготовления плиты
Пролет плиты – 6,3 м.
Ширина плиты – 1,5 м.
Ширина балок – 0,3 м.
Класс бетона – В25.
Расчетное сопротивление бетона RB = 14,5 МПа (3, табл. 13),
RBt = 1,05 МПа (3, табл. 13).
Сопротивление бетона при расчете по 2-ой группе предельных состояний: RB,ser = 18,5 МПа (3, табл. 12), RBt,ser = 1,6 МПа (3, табл. 12). Модуль деформации бетона ЕB = 27000 МПа (3, табл. 18). Класс предварительно напрягаемой арматуры А-IV.
Сопротивление напрягаемой арматуры: RSP=510 МПа и RSС=450 МПа (3, табл. 22), RS,SER=590 МПа (3, табл. 19). Модуль деформации ES=190000 МПа (3, табл. 29). Класс ненапрягаемой арматуры Вр-I. Влажность воздуха окружающей среды менее 75% - γb2=0,9 (3, табл. 15). Формирование плит на металлическом поддоне с теплообработкой – в тоннельных камерах. Натяжение арматуры – на упорах электротермическим способом.
Нагрузка на 1 м2 плиты приведена в таблице 1.1.
2.2 Назначение основных размеров плиты
Расчетный пролет (крайняя плита):
![]() м
м
Высота плиты:
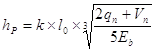 ,
,
где k = 8 ... 10 (пустотные плиты); qn – нормативная продолжительная нагрузка (постоянная и длительная) в кН/м2; Vn – нормативная кратковременная нагрузка в кН/м2.
![]() м.
м.
Принимаем hn = 0,25 м.
Основные размеры поперечного сечения плиты (назначены по рекомендациям (1, прил. 3)) показаны на рис. 2.1.
Проверка: 7 х 170 + 6 х 30 + 2 х 60=1490 мм.
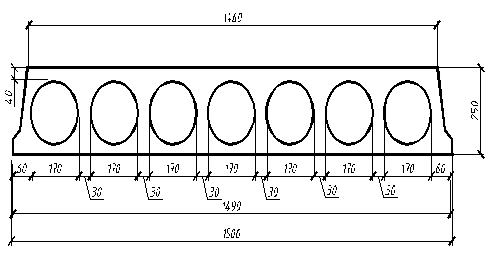
Рис. 2.1 Поперечное сечение плиты
2.3 Расчет по 1-ой группе предельных состояний
2.3.1 Расчет полки плиты на изгиб
Для расчета выделяют полосу плиты шириной в один метр. Сбор нагрузок на полку плиты приведён в таблице 1.3.
Таблица 1.3 Загружение полки плиты
Наименование нагрузок | qn кН/м | gf | q кН/м |
| Вес пола (см. табл. 1) | 1,2 | - | 1,46 |
| Вес полки (0,03´25) | 0,75 | 1,1 | 0,825 |
| 3. Временная нагрузка | 3,8 | 1,2 | 4,56 |
Итого ´ gn | 5,75 | 6,845 |
Изгибающий момент (рисунок 2.2):
![]() кНм
кНм
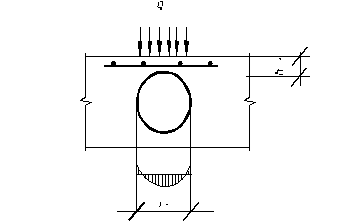
Рис. 2.2 - Схема работы полки плиты
Полезная высота сечения при расположении арматуры в середине полки:
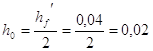 м.
м.
Подбор сечения арматуры:
![]()
![]()
![]() м2.
м2.
Принимаем минимальную сварную сетку по ГОСТ 8478-8 (4, приложение VII) ![]() (Аs=0,65 см2).
(Аs=0,65 см2).
2.3.2 Предварительный подбор сечения продольной арматуры
Изгибающий момент в середине пролета:
![]() кНм.
кНм.
В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки приведенного таврового сечения (рис. 2.3) принимается равной фактическому значению (![]() ). Ширина полки bf’, вводимой в расчет, принимается равной всей ширине верхней полки плиты, так как имеет место:
). Ширина полки bf’, вводимой в расчет, принимается равной всей ширине верхней полки плиты, так как имеет место: 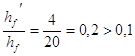 (3, п.3.16). Ширина ребра b=1,46 - 7´0,17 = 0,27 м.
(3, п.3.16). Ширина ребра b=1,46 - 7´0,17 = 0,27 м.
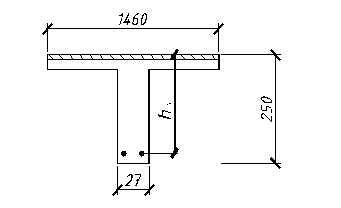
Рис. 2.3 - Сжатая полка сечения плиты
Предположим, что нейтральная ось проходит в пределах полки (I случай), то есть ![]() (1, 3.3).
(1, 3.3).
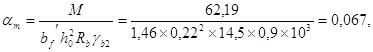
где ![]() см
см
![]()
![]() см, подтверждается 1-ый случай расчета.
см, подтверждается 1-ый случай расчета.
Для вычисления коэффициента условия работы gsb по формуле
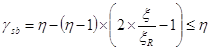 , (3, 27)
, (3, 27)
принимаем предварительно xR=0,55. Для арматуры класса A-IV коэффициент h=1,2 (3, п.3.13). Тогда
![]() Принимаем gsb=1,2.
Принимаем gsb=1,2.
Требуемое сечение арматуры равно:
![]()
Принимаем 6Æ10A-IV (Asp=4,74 см2) (прил. 4). Размещение арматуры приведено на рисунке 2.4.
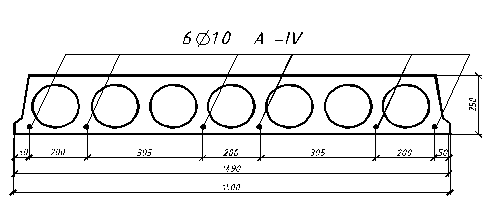
Рис. 2.4 - Размещение рабочей арматуры.
2.3.3 Определение характеристик приведённого сечения
Заменяем пустоты равновеликими по площади и моментам инерции прямоугольниками. При круглых пустотах диаметрами d сторона квадратного отверстия равна: hred=0,9d=0,9´17=15,3 см.
Толщина полок, приведенного сечения hf = hf’=(25-15,3)´0,5=4,85 см.
Ширина ребра 146-7´15,3=38,9 см (рисунок 2.4).
![]() (3, п. 4.5)
(3, п. 4.5)
![]()
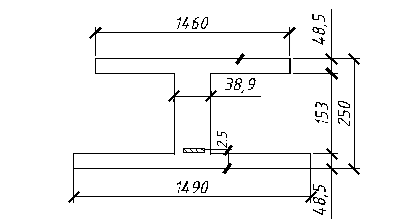
Рис. 2.4. Приведенное сечение плиты
Приведенная площадь сечения:
![]()
![]() м2.
м2.
Приведенный статический момент относительно нижней грани сечения:
![]()
![]() м3.
м3.
Положение центра тяжести приведенного сечения:
![]() м.
м.
Приведенный момент инерции:
![]()
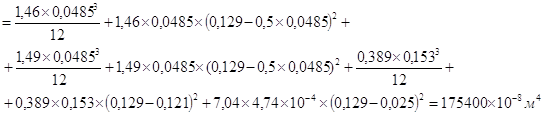
Момент сопротивления по нижней зоне
![]() м3,
м3,
то же по верхней зоне
![]() м3.
м3.
2.3.4 Назначение величины предварительного напряжения арматуры
Для арматуры должны выполняться условия:
![]() и
и ![]() (3, 1)
(3, 1)
где значение допустимых отклонений Р при электротермическом способе принимается (3, п.1.23):
![]() МПа (3, 2). Тогда
МПа (3, 2). Тогда
![]() МПа,
МПа,
![]() МПа.
МПа.
Принимаем ssp =500 МПа.
2.3.5 Определение потерь предварительного напряжения
Первые потери (![]() ):
):
1. От релаксации напряжений арматуры. При электротермическом натяжении стержневой арматуры:
s1=0,03ssp=0,03´500=15 МПа (3, поз.1 табл.5).
2. От температурного перепада потери не учитываются, так как форма с изделием подогревается в тоннельной камере до одинаковой температуры.
3. От обмятия анкеров. При электротермическом способе натяжения в расчете не учитывается ![]() (3, табл.5, поз.3).
(3, табл.5, поз.3).
4. От сил трения арматуры. При натяжении на упоры и отсутствии огибающих приспособлений не учитываются ![]() (3, табл.5, поз.4).
(3, табл.5, поз.4).
5. От деформации стальной формы. При электротермическом способе натяжения в расчете не учитываются ![]() (3, табл.5, поз.5).
(3, табл.5, поз.5).
6. От быстронатекающей ползучести бетона (3, табл.5, поз.6). Напряжения в бетоне на уровне центра тяжести предварительно напряженной арматуры sbp равны
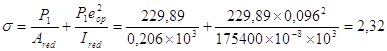 МПа, (4, п.33)
МПа, (4, п.33)
где ![]() м,
м,
![]() кН,
кН,
![]() МПа.
МПа.
Передаточная прочность бетона Rbp для арматуры A-IV назначается по (3, п.2.6) из условия Rbp³ 11 МПа, Rbp³ 0,5B25 =12,5 МПа.
Принимаем Rbp=12,5 МПа.
![]() .
.
Так как ![]() , то
, то ![]() МПа
МПа
Суммарные первые потери ![]() МПа.
МПа.
Вторые потери:
7. От усадки бетона (3, табл.5, поз.8). Для В25 < В35 и при тепловой обработке изделия при атмосферном давлении s8=35 МПа.
8. От ползучести бетона (3, табл.5, поз.9).
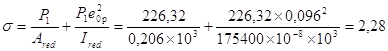 МПа,
МПа,
где ![]() кН
кН
Так как sbp/Rbp=2,28/12,5=0,182 < 0,75, то
![]() МПа,
МПа,
где a = 0,85 - при тепловой обработке бетона.
Суммарные вторые потери slos2 = 23,25 + 35 = 58,25 МПа.
Общие потери slos=slos1 + slos2 =22,42 + 58,25 =80,67 МПа. В соответствии с (3, п.1.2.5) принимаем slos = 100 МПа.
2.3.6 Проверка прочности бетона в стадии обжатия
Напряжения в бетоне на уровне крайнего сжатого волокна после отпуска арматуры равны (2, п.1.29):
![]()
![]() МПа (4, п.36)
МПа (4, п.36)
Т.к. неравенство ![]() (3, табл.7, п.1.29) выполняется, прочность бетона в стадии обжатия обеспечена.
(3, табл.7, п.1.29) выполняется, прочность бетона в стадии обжатия обеспечена.
2.3.7 Определение коэффициента точности натяжения арматуры
Коэффициент точности натяжения арматуры gsp определяется по формуле: ![]() . (3, 6)
. (3, 6)
При электротермическом способе натяжения
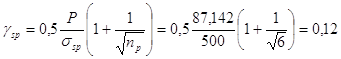 , (3, 7)
, (3, 7)
где np =6 –число стержней напряженной арматуры
тогда gsp = 1 ± 0,12.
2.3.8 Проверка принятого сечения предварительно напряженной арматуры
Ранее было принято xR = 0,55. Необходимо уточнить значения коэффициента xR и площади сечения арматуры Asp.
Коэффициент xR определяем по формуле:
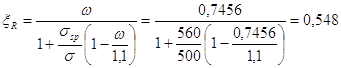 (3, 25 и 69)
(3, 25 и 69)
где ![]() МПа,
МПа,
![]() - с учетом полных потерь; при неавтоматизированном электротермическом натяжении арматуры Δ
- с учетом полных потерь; при неавтоматизированном электротермическом натяжении арматуры Δ![]() (3, п.3.28);
(3, п.3.28);
![]()
ssc,u= 500 МПа (3, п.3.12).
Поскольку полученное значение совпадает со значением, принятым в п.2.3.2 xR=0,55, то перерасчет арматуры не требуется.
.
2.3.9 Расчет прочности плиты по сечению наклонному к продольной оси по поперечной силе
Расчетная поперечная сила на опоре равна:
![]() кН.
кН.
Влияние свесов сжатых полок (при 7 отверстиях, с учетом ![]() )
)
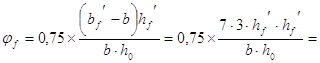
![]() (3, 77)
(3, 77)
Влияние усилия обжатия продольной предварительно напряженной арматуры
![]() , (3, 78)
, (3, 78)
где ![]() МПа.
МПа.
Вычисляем ![]() . Принимаем 1,5,
. Принимаем 1,5,
Вычисляем
![]() =
=![]() кН.
кН.
Так как ![]() кН, то поперечная арматура по расчету не требуется и она ставится конструктивно (3, п.5.27). На приопорных участках длиной
кН, то поперечная арматура по расчету не требуется и она ставится конструктивно (3, п.5.27). На приопорных участках длиной ![]() =6,3/4=1,575 м необходимо установить 4 каркаса Æ4Вр-I с шагом
=6,3/4=1,575 м необходимо установить 4 каркаса Æ4Вр-I с шагом ![]() см (рисунок 2.5). В середине пролета поперечная арматура не требуется.
см (рисунок 2.5). В середине пролета поперечная арматура не требуется.
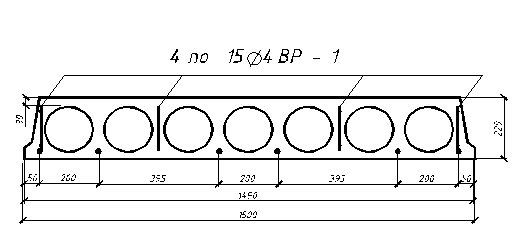
Рис. 2.5 - Распределение поперечной арматуры.
2.3.10 Проверка прочности по сжатой полосе между наклонными трещинами
Расчет производится по формуле:
![]()
![]() кН (3, 72)
кН (3, 72)
где ![]() ,
,
![]() ,
,
![]() =4х0,126х10-4=0,504х10-4м2 – площадь поперечной арматуры.
=4х0,126х10-4=0,504х10-4м2 – площадь поперечной арматуры. ![]() (3, 74),
(3, 74),
где β =0,1 для тяжелого бетона
Условие выполняется, прочность между наклонными трещинами обеспечивается.
2.3.11 Расчет плиты в стадии изготовления
При распалубке и снятии изделия с формы подъемными петлями плита работает, как консольная балка (рис. 2.6). Вылет консоли lc=0,4 м. Изгибающий момент от собственного веса плиты в основании консоли с учетом коэффициента динамичности kd=1,4 (3, п.1.13) равен:
![]() кНм.
кНм.
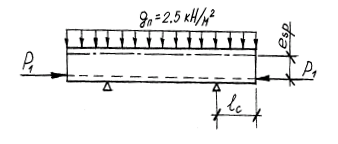
Рис. 2.6 - Работа плиты при распалубке
Напряжение в напрягаемой арматуре в сжатой зоне равно:
![]() МПа (3, п.3.14), где при расчете элементов в стадии обжатия ssc,u=330 МПа (3, п.3.12); ssp’ определяется с учетом потерь до обжатия с коэффициентом gsp > 1 (3, п.3.14), то есть
МПа (3, п.3.14), где при расчете элементов в стадии обжатия ssc,u=330 МПа (3, п.3.12); ssp’ определяется с учетом потерь до обжатия с коэффициентом gsp > 1 (3, п.3.14), то есть ![]() (2.3.7). Таким образом, после обжатия бетона в арматуре остаются растягивающие напряжения.
(2.3.7). Таким образом, после обжатия бетона в арматуре остаются растягивающие напряжения.
Усилие предварительного напряжения рассматривается как внешняя сила: ![]() кН.
кН.
Изгибающий момент в консоли относительно верхней арматуры
![]() кНм,
кНм,
Вычисляем ![]()
и ![]() ,
,![]()
где Rb определяется по классу бетона (3, табл.13) равной отпускной прочности Rbp=12,5 МПа; gb8=1,2 (3, табл.15, поз.8).
Требуемое сечение арматуры в верхней зоне плиты, как для внецентренно сжатого элемента:
![]() .
.
Оставляем ранее принятую арматурную сетку (п.2.3.1).
2.4 Расчет плиты по 2-ой группе предельных состояний
2.4.1.Проверка на образование начальных трещин в сжатой зоне при эксплуатационных нагрузках в стадии изготовления
После освобождения арматуры на упорах под действием силы обжатия Р1 плита изгибается, и в верхней зоне могут возникнуть начальные трещины.
Трещины не возникнут, если удовлетворится условие:
![]() (3, 124),
(3, 124),
где момент от внешних сил (собственного веса):
![]() кНм,
кНм,
Момент силы Р1 относительно ядровой точки, наиболее удаленной от растянутой (верхней) зоны:
![]() кНм,
кНм,
где Р1=226,32 кН (п.2.3.5); ![]() =0,096 м (п. 2.3.5).
=0,096 м (п. 2.3.5).
Расстояние до нижней ядровой точки
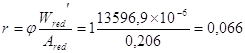 м; (3, 132)
м; (3, 132)
коэффициент ![]() >1, (3, 145)
>1, (3, 145)
максимальное напряжение в сжатом бетоне от внешних сил и сил предварительного напряжения (нижняя зона):
![]()
![]() .
.
Принимаем j = 1,0.
Определим упруго пластический момент сопротивления ![]() по упрощенной формуле:
по упрощенной формуле: ![]()
При 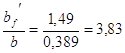 и
и ![]() имеем g = 1,5 (1, прил.5), тогда
имеем g = 1,5 (1, прил.5), тогда
![]() м3.
м3.
![]() ,
,
6,7896 - 18,6 = -11,81 < 21728![]() =21,73
=21,73
где ![]() МПа при отпускной прочности бетона Rbp =12,5 МПа (3, табл.13).
МПа при отпускной прочности бетона Rbp =12,5 МПа (3, табл.13).
Т.к. неравенство выполняется, то начальные трещины не возникают.
Необходимо также проверить появление начальных трещин в местах установки подъемных петель:
Поскольку Mq=0,42 кНм (п.2.3.11),
![]()
![]() кНм (3, 125), начальные трещины не возникают.
кНм (3, 125), начальные трещины не возникают.
2.4.2 Расчет нормальных сечений на образование трещин при эксплуатационной нагрузке
Изгибающий момент от внешних нагрузок (3, п.4.5) при gf = 1
![]() кНм,
кНм,
в том числе от длительно действующих нагрузок
![]() кНм
кНм
Момент сил обжатия относительно верхней ядровой точки равен:
![]()
![]() кНм, (3, 129)
кНм, (3, 129)
где Р2 = 189,36 кН (п.2.3.9).
Расстояние до верхней ядровой точки
![]() м (3, 132)
м (3, 132)
![]()
Принимаем j = 1, (3, 135)
sb - максимальные напряжения в сжатой зоне бетона (верхней)
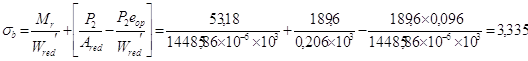
Упругопластический момент сопротивления относительно нижней растянутой зоны равен:
![]() м3.
м3.
Проверка образования трещин производится из условия:
![]() (3, 124),
(3, 124),
где ![]() кНм (3, 125).
кНм (3, 125).
Так как условие (3, 124) удовлетворяется при длительной части нагрузки
(39 < 61,82), и при полной нагрузке (53,18< 61,82), в элементе трещины не возникают.
2.4.3 Расчет наклонных сечений на образование трещин
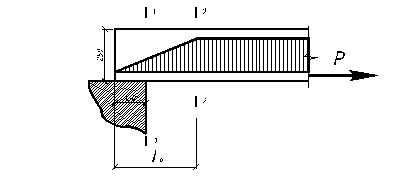
Расчет производится в сечении у грани опоры плиты (I-I) и на расстоянии длины зоны передачи напряжений в сечении (2-2) (рис. 2.7). (3, п.4.11)
Длина зоны передачи напряжений равна:
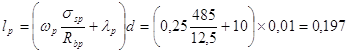 м, (3, 11)
м, (3, 11)
![]()
Рис. 2.7 - Определение напряжения в арматуре.
где ![]() и
и ![]() (3, табл.28)
(3, табл.28)
![]() МПа (с учетом потерь поз. 1-5) (3,табл.5);
МПа (с учетом потерь поз. 1-5) (3,табл.5);
![]() (3, п.2.6).
(3, п.2.6).
Определение нормальных напряжений в бетоне от внешней нагрузки и усилия предварительного обжатия на уровне центра тяжести приведенного сечения (У=0): в сечении 2-2
![]() МПа,
МПа,
в сечении 1-1
![]() МПа,
МПа,
Определение касательных напряжений в бетоне от внешней нагрузки:
![]() МПа,
МПа,
![]() кН,
кН,
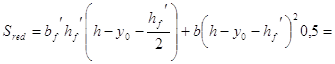
![]()
Значение главных напряжений (растягивающих smt и сжимающих smc) в бетоне: в сечении 2-2
![]() МПа,
МПа,
![]() МПа,
МПа, ![]() МПа.
МПа.
В сечении 1-1:
![]() МПа,
МПа,
![]() МПа,
МПа, ![]() МПа.
МПа.
Определение коэффициента влияния двухосного сложного напряженного состояния на прочность бетона:
в сечении 2-2
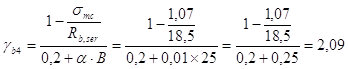 ; (3, 142)
; (3, 142)
где a = 0,01 для тяжелого бетона. Принимаем gb4=1, (3, 142),
в сечении 1-1
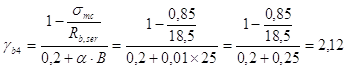
Принимаем gb4 = 1.
Проверка образования трещин наклонных к продольной оси элемента производится из условия ![]() (3, 141)
(3, 141)
В сечении 1-1: ![]() МПа
МПа![]() МПа - трещин нет.
МПа - трещин нет.
В сечении 2-2: ![]() МПа
МПа![]() МПа - трещин нет.
МПа - трещин нет.
2.4.4 Определение прогиба плиты при отсутствии трещин в растянутой зоне
Определение кривизны от кратковременной нагрузки (2,0 кН/м2) (3, 4.24)
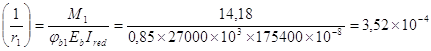 1/м, (3, 156)
1/м, (3, 156)
где изгибающий момент от временной нагрузки:
![]() кНм,
кНм,
jb1 = 0,85 - коэффициент, учитывающий влияние кратковременной ползучести бетона.
Опре
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Проектирование многоэтажного здания
- Проектирование неутепленного здания с несущими деревянными гнутоклееными рамами ступенчатого очертания
Данная курсовая работа представляет собой изучение проектирования неутепленного здания с несущими деревянными гнутоклееными рамами с
- Проектирование одноэтажного здания с несущим деревянным каркасом
- Проектирование оснований и конструирование фундаментов промышленных зданий и сооружений
- Проектирование оснований и фундаментов восьмиэтажного жилого дома
- Проектирование оснований и фундаментов многоэтажного гражданского здания
- Проектирование основания и фундамента 13-этажного жилого дома в городе Великий Устюг
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

