Скачать

Применение магнетронных генераторов большей мощности в радиолокационных системах

В связи с развитием авиации, появлением новых высокоскоростных самолетов в настоящее время огромное внимание уделяется вопросам безопасности полетов и разработке новых систем обеспечения.

Существующие радиолокаторы, предназначенные для выявления небезопасных для полета областей активной грозовой деятельности, определения угла заноса самолета, а так же наблюдения за земной поверхности с целью ориентирования не могут решать поставленные задачи из-за малой дальности действия. По этому весьма актуальным вопросом является применение в существующих радиолокаторах магнетронов большей мощности. Возможна модернизация существующих радиолокаторов, которые выполнены в виде функционально законченных и в соответствующих комплектациях устанавливаются на самолетах гражданской и транспортной авиации Як-40, Як-42, Ил-62, Ил-86, Ан-24, Ан-26, Ан-30, Ан-32, Ту-134, Ту-154.

1 АНАЛИЗ МАГНЕТРОННЫХ ГЕНЕРАТОРОВ

Магнетронные генераторы, находящие сейчас широкое применение, имеют большую и сложную историю развития.

Поведение диодов в магнитном поле явилось предметом многочисленных опытов вскоре после создания первых электронных ламп. Сверхвысокочастотные колебания в диодах, помещенных в постоянное магнитное поле, были обнаружены еще в 1920—1924 гг. Толчком к этим исследованиям в значительной мере явились эксперименты по возбуждению колебаний в схеме тормозящего поля.

Установлено, что существуют три основных типа колебаний в магнетронах, различающихся своим электронным механизмом:

1)колебания циклотронного типа;

2)колебания типа отрицательного сопротивления;

3)колебания типа бегущей волны.

Наибольший практический интерес представляют колебания типа бегущей волны, которые происходят в многорезонаторных магнетронах, разработанных впервые в 1938—1940 гг. Н. Ф. Алексеевым и Д. Е. Маляровым. Этому типу колебаний уделяется в дальнейшем основное внимание.

Развитие многорезонаторных магнетронов привело к разработке мощных высокоэффективных автогенераторов, играющих важнейшую роль в технике СВЧ. Вместе с тем разработки и исследования магнетронных генераторов стимулировали появление большого класса приборов СВЧ магнетронного типа — ламп бегущей волны М-типа, ламп обратной волны М-типа и платинотронов. Общим признаком магнетронов и других приборов М-типа является присутствие в междуэлектродном пространстве скрещенных постоянных электрического и магнитного полей.

Устройство типичного многорезонаторного магнетрона показано схематически на рисунке 1.1. Анодом магнетрона является сплошной цилиндрический медный блок, разделенный на сегменты продольными щелями. Эти щели входят в состав полых резонаторов, расположенных на равных расстояниях по окружности анода. Катод магнетрона имеет цилиндрическую форму и расположен внутри анода вдоль его оси.

Постоянное магнитное поле В направлено вдоль оси прибора, т. е. перпендикулярно плоскости чертежа на второй проекции (рис. 1.1).

Постоянное или импульсное анодное напряжение приложено между катодом и анодом и создает электрическое поле, перпендикулярное к направлению магнитного поля. Вывод СВЧ энергии производится обычно от одного из резонаторов, например, с помощью петли и коаксиальной линии.

Анализ работы многорезонаторных магнетронов показывает, что их действие можно наглядно рассматривать на основе бегущих волн, распространяющихся по внутренней поверхности анодного блока, обращенной к катоду. Это и послужило основанием для названия "колебания типа бегущей волны".

В пространстве взаимодействия между катодом и анодом магнетронов происходят все процессы, которые должны присутствовать в любом электронном генераторе и усилителе СВЧ: управление электронным потоком, образование сгустков и отдача энергии высокочастотному электрическому полю. В магнетронах нет разделенных в пространстве областей управления, группировки и отдачи энергии, которые имеются, например, в клистронах. Это обстоятельство, наряду со сложным характером движения электронов, значительно осложняет изучение процессов в магнетронах. Тем не менее, пользуясь представлениями о видах колебаний и методом эквивалентных схем в сочетании с расчетом движения электронов, оказывается возможным и в этом случае использовать общие методы.

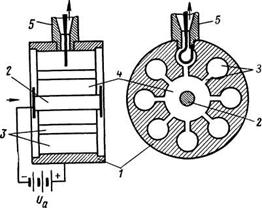
Рисунок 1.1 - Схема устройства и включения магнетронного генератора: 1-анодный блок; 2-катод; 3-резонатор типа щель-отверстие; 4- пространство взаимодействия; 5 – вывод энергии

1.1 Движение электронов в статическом магнетроне

Прежде чем перейти к проблеме возбуждения СВЧ колебаний, рассмотрим задачу о движении электронов в скрещенных электрическом и магнитном полях в отсутствие колебаний.

Катод магнетрона, как правило, имеет цилиндрическую форму и расположен концентрично внутри цилиндрического анода. Отвлечемся от искажений постоянного электрического поля, вызываемых щелями в поверхности анода, и рассмотрим систему со сплошным анодом, изображенную на рисунке 1.2, а. Постоянное магнитное поле предположим направленным точно вдоль оси г. Пространственный заряд, создаваемый двигающимися электронами, учитывать не будем.

Пренебрегать действием пространственного заряда (коллективным взаимодействием электронов) в электронных приборах можно лишь с известной осторожностью. Особенно важно помнить об этом в случае магнетрона, так как под действием магнитного поля пространственный заряд может значительно увеличиться. Однако строгое решение задачи магнетрона с учетом пространственного заряда наталкивается на большие трудности. Многие важные свойства магнетронов могут быть рассмотрены независимо от присутствия и распределения пространственного заряда.

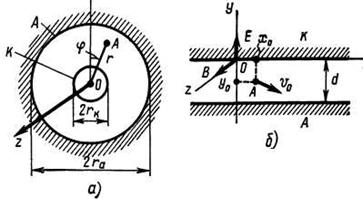
Рисунок 1.2 - К расчету движения электронов в цилиндрическом и плоском магнетронах со сплошным анодом в статистическом режиме. Электрон находится в точке А

Электроны эмитируются катодом с очень малыми начальными скоростями, поэтому величиной начальной скорости в статистическом режиме магнетрона можно сразу пренебречь. Однако при рассмотрении других ламп СВЧ со скрещенными электрическими и магнитным полями полезно общее решение, учитывающее начальную скорость электрона, начавшего свое движение из произвольной точки в пределах пространства взаимодействия. Учет начальных скоростей необходим также при анализе сортировки электронов в магнетронных генераторах в присутствии колебаний.

Расчеты движения электронов производится с наиболее простой плоской системы, изображенной на рис. 1.2, б. Рассмотрение плоского магнетрона важно не только с точки зрения простоты математического решения. Большинство современных магнетронов имеют катоды большого диаметра, что позволяет приближенно заменить катод и анод параллельными плоскостями.

1.2 Условия самовозбуждения

Рассмотрим сначала случай, когда отношение радиусов катода и анода магнетрона близко к единице, т. е. система электродов близка к плоской. Примем, что условием отдачи электронами максимальной энергии высокочастотному полю является совпадение фазовой скорости бегущей волны и средней скорости движения электронов в отсутствие колебаний. При этом всякое первоначальное колебание, возникающее в анодном блоке магнетрона, должно нарастать до тех пор, пока не начнут действовать ограничивающие нелинейные эффекты.

Используем уравнение, определяющее фазовую скорость волны -вида -й пространственной гармоники. Чтобы получить условие усредненного синхронизма между электронами и волной, вместо радиуса анода r_а подставим средний радиус пространства взаимодействия, равный

. (1.1)

Таким образом, средняя фазовая скорость волны в пространстве взаимодействия составляет:

. (1.2)

Средняя скорость движения электронов равна . Отсюда условие синхронизма может быть записано в виде:

. (1.3)

В рассматриваемой системе напряженность постоянного электрического поля можно выразить в виде  Подставляя эту величину в предыдущее уравнение и учитывая, что генерируемая частота определяется в основном резонансной частотой данного вида колебаний, т.е. что , имеем:

 (1.4)

Согласно этому уравнению анодное напряжение, при котором должно происходить самовозбуждение многорезонаторного магнетрона, для каждого вида колебаний при фиксированном номере гармоники линейно связано с индукцией магнитного поля. Отношение есть величина постоянная для данного магнетрона при заданных значениях и .

На рисунке 1.3, а построены соответствующие графики для трех видов колебаний 8-резонаторного магнетрона при  Здесь же построена парабола критического режима.

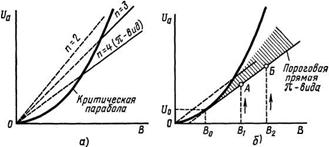
Рисунок 1.3 - Самовозбуждение магнетрона: а ) – для упрощенного случая при N=8, б)– для -вида колебаний

Прямые, определяемые уравнением (1.4), проходят через начало координат и пересекают критическую параболу. С физической точки зрения понятно, что при  генерация колебаний типа бегущей волны невозможна: все электроны попадают на анод не позднее чем через половину периода циклоидального колебания. Поэтому условиям самовозбуждения отвечают лишь участки прямых, выделенные на рисунке 1.3, а сплошными линиями и лежащие ниже параболы критического режима.

Рассмотренные графики самовозбуждения не могут претендовать на большую точность, а можно лишь установить, что для каждого вида колебаний существуют оптимальные соотношения между постоянным анодным напряжением и индукцией магнитного поля. Это не означает, однако, что генерирование колебаний невозможно в точках плоскости (f/_a, В), не лежащих на указанных прямых. Если увеличивать анодное напряжение при неизменной индукции магнитного поля, то генерируемая мощность на данном виде колебаний должна переходить через максимум и уменьшаться при удалении от прямой, определяемой уравнением (1.4). При дальнейшем увеличении напряжения £/_а могут быть достигнуты условия синхронизма с полем волны следующего вида, имеющего более низкий номер п.Естественно предположить, что существует промежуточная область неустойчивой генерации, где небольшие изменения анодного напряжения и постоянного анодного тока приводят к скачкообразному переходу с одного вида колебаний на другой.

Отвлекаясь от возбуждения колебаний на пространственных гармониках, отметим, что -вид колебаний требует для своего возбуждения наименьшего анодного напряжения. Это свойство -вида играет большую роль, особенно при работе магнетронов в импульсном режиме. Одновременно можно сделать вывод, что -вид отделен от других видов колебаний не только по частоте, но и по величине анодного напряжения.

1.3 К.П.Д. магнетрона

Трудности, связанные с прямым вычислением отдаваемой электронами мощности, настолько велики, что в настоящее время не существует строгого расчета электронного к. п. д. магнетрона типа бегущей волны. В подобных случаях можно вычислить мощность, рассеиваемую электронами после взаимодействия с полем, и затем использовать закон сохранения энергии

Рассмотрим кинетическую энергию, которую имеет электрон в момент удара об анод после того, как значительная часть потенциальной энергии электрона отдана высокочастотному полю в пространстве взаимодействия.

При обсуждении процессов сортировки электронов было показано, что циклоидальная траектория благоприятного электрона при малой амплитуде высокочастотных колебаний наклоняется в сторону анода, но остается в основном такой же, как в статическом режиме. Радиус катящегося круга в плоском магнетроне равен

, (1.5)

где  - расстояние между катодом и анодом.

Скорость, которую имеет электрон при ударе об анод, зависит от момента удара. Будем исходить из наихудшего с точки зрения величины к. п. д. случая, когда удар происходит в верхней точке циклоидальной траектории. Полюсом вращения является точка касания круга к плоскости, по которой происходит качение этого круга. Радиус вращения электрона равен здесь . Зная угловую скорость вращения круга  нетрудно получить максимальную скорость электрона:

. (1.6)

К такому же результату можно придти, исходя из известной скорости центра круга, равной .

Максимальная кинетическая энергия, рассеиваемая электроном на аноде, равна

 (1.7)

Тот же электрон, находясь на катоде до начала движения в пространстве взаимодействия, обладал по отношению к аноду потенциальной энергией, равной W_n= eU_a, при нулевой кинетической энергии. Следовательно, энергия, отданная высокочастотному полю, по закону сохранения энергии равна W_n—.

К. п. д. рассматриваемого одиночного электрона, таким образом, имеет величину

 (1.8)

Полученное уравнение можно преобразовать, выразив величину  через критические параметры и .

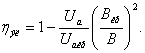 (1.9)

Уравнение (1.9) показывает связь электронного к.п.д. магнетрона с постоянным анодным напряжением и индукцией магнитного поля. При В = В_крэлектронный к.п.д. равен нулю, что вполне согласуется с делавшимися предположениями. Чем больше режим магнетрона отличается от критического, тем выше должен быть электронный к.п.д. Особенно интересно, что никакого теоретического предела повышения величины _эл для магнетрона по рассматриваемым уравнениям не существует.

Зависимость электронного к.п.д. магнетрона от величины магнитного поля В можно сделать особенно наглядной, если учесть условие синхронизма при работе на любом фиксированном виде колебаний. Воспользуемся упрощенным условием самовозбуждения магнетрона:

 (1.10)

Вводя это соотношение в (1.8) и полагая для цилиндрической системы  имеем при

 (1.11)

где - отношение радиуса катода к радиусу анода, равное .

Подставим в (1.11) величины е и m, а также введем резонансную длину волны - говида колебаний .

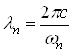Выражая индукцию магнитного поля в тесла и длину волны в сантиметрах, получаем:

 (1.12)

Для оценки получаемого к.п.д. рассмотрим в качестве примера 8-резонаторный магнетрон 10-см диапазона, работающий на -виде колебаний при магнитной индукции 0,18 тл (1800 гс). Величину примем равной 1/3; такая или близкая к ней величина типична для магнетронов при N = 8. Вычисления по (1.12) дают: 70%.

Расчетные значения электронного к.п.д. по (1.11) и (1.12) обычно несколько превышают получаемую на практике величину . Отчасти это и понятно, так как в рассмотренном расчете не были учтены потери энергии за счет неблагоприятных электронов, бомбардирующих катод, а также непроизводительные потери электронов на боковые крышки магнетрона и некоторые другие факторы. Величина электронного к.п.д. существующих магнетронов сантиметрового диапазона составляет 50—70%, а в некоторых случаях и более. Столь высокая эффективность магнетронов делает их ценнейшим мощным автогенератором диапазона СВЧ. Для данного магнетрона при неизменной длине волны уравнение (1.11) можно переписать в виде

 (1.13)

Полученное уравнение соответствует случаю, когда к.п.д. отсчитывается при движении вдоль одной из прямых самовозбуждения на плоскости (U_a, В) (см. рис. 1.3, а). Соответствующее графическое изображение зависимости _эл = f(B) для 8-резонаторного магнетрона показано на рисунке1.4, а. Кривые электронного к.п.д. имеют вид отрезков гипербол. Чем ниже номер вида п, тем меньше электронный к.п.д. при одной и той же величине магнитной индукции В. Иначе говоря, для достижения одного и того же электронного к.п.д. наименьшее магнитное поле требуется при -виде колебаний.

Рисунок 1.4 - Зависимость электронного к.п.д магнетрона от индукции магнитного поля при const

Рост электронного к. п. д. магнетрона при увеличении магнитной индукции В и, напомним, при соответствующем повышении постоянного анодного напряжения _алегко понять с физической точки зрения, так как при этом происходит неограниченное уменьшение радиуса катящегося круга и уменьшение энергии, рассеиваемой электронами на аноде. Такие же тенденции характерны для работы других приборов магнетронного типа. В этом отношении проявляются очевидные отличия и преимущества приборов М-типа в сравнении с приборами О-типа. В приборах М-типа электроны отдают СВЧ полю не кинетическую, а потенциальную энергию, полученную от источника постоянного напряжения. Средняя скорость переносного движения электронов не изменяется, благодаря чему не нарушаются условия синхронизма с полем бегущей волны.

Опыт в основном подтверждает ход зависимости _эл= f(B) при , представленной на рисунке 1.4, а. Однако в случае разнорезонаторных магнетронов в некотором интервале значений магнитной индукции наблюдается "провал" электронного к. п. д., как показано качественно на рисунке 1.4, б. Исследования показали, что в центре "провала" произведение магнитной индукции, выраженной в тесла, на длину волны в сантиметрах имеет для всех магнетронов одинаковую величину, равную приблизительно 1,2 тл.см.

"Провал" электронного к. п. д. в разнорезонаторных магнетронах можно качественно объяснить с точки зрения циклотронного резонанса, возникающего при условии . В пространстве взаимодействия разнорезонаторного магнетрона, кроме поля -вида, имеется составляющая поля п = 0. При приблизительном совпадении частоты генерируемых колебаний и циклотронной частоты характер движения электронов может измениться. Большую роль играет тот факт, что поле нулевой составляющей значительно медленнее убывает при удалении от анода, чем поле -вида .

Форма спиц и их взаимодействие с полем -вида ухудшаются.

Обычно разнорезонаторные магнетроны эксплуатируются при более низком магнитном поле, чем поле, соответствующее центру "провала". Перейти в область больших индукций за "провалом" практически не удается из-за трудностей получения очень сильных магнитных полей.

Некоторое влияние на величину электронного к. п. д. магнетрона оказывает разделение видов колебаний. По-видимому, условия формирования спиц ухудшаются при наличии "загрязняющих" полей в пространстве взаимодействия. Электронный к. п. д. магнетрона может снизиться также за счет влияния поля связок около концов анодного блока. Это поле, не имеющее азимутальных вариаций, оказывает примерно такое же воздействие на пространственный заряд в магнетроне, какое имеет поле нулевой составляющей в магнетронах разнорезонаторной конструкции. Для устранения подобных эффектов связки обычно экранируются путем расположения их в кольцевых канавках, выточенных на торцах анодного блока.

Диаметр катода также влияет на величину электронного к. п. д. Для повышения величины желательно уменьшать отношение . Однако при малом - не могут полностью удовлетворяться условия синхронизма между электронами и полем, так как напряженность постоянного электрического поля имеет наибольшую величину у катода и уменьшается по направлению к аноду. Чтобы повысить электронный к. п. д. магнетрона, обычно рекомендуется выбирать наименьшую возможную величину, при которой получается достаточная устойчивость видов колебаний.

Для оценки оптимального отношения с предложены различные эмпирические соотношения, например:

 (1.14)

где N — число резонаторов. Отметим, однако, что зависимость эл = f() не очень критична и допускает заметные отклонения от величины, рассчитанной по уравнениям (1.14).

В заключение напомним, что полный к. п. д. магнетрона определяется с учетом к. п. д. резонаторной системы:

 (1.15)

Как известно, величина  в общем случае связана с собственной, нагруженной и внешней добротностями колебательной системы соотношением

 (1.16)

Величина внешней добротности выбирается с учетом допустимого затягивания частоты магнетрона и обычно не бывает ниже 100—200. Собственную добротность  желательно иметь как можно выше. Типичная величина в сантиметровом диапазоне имеет порядок 1000. Таким образом, по (1.16) к. п. д. резонаторной системы может составлять от 90—95% до 60—65% на наиболее коротких волнах. Типичные значения полного к. п. д. магнетронов составляют от 60—70% на дециметровых волнах до 20—30% на волнах длиной порядка 1 см.

1.4 Рабочие и нагрузочные характеристики магнетронов

При рассмотрении эксплуатационных свойств магнетронов используют две группы характеристик. К первой относятся вольтамперные характеристики, снятые при неизменной нагрузке, соответствующей режиму согласования выходного устройства магнетрона. Параметрами при снятии характеристик  являются магнитная индукция В, генерируемая мощность Р_ген, частота генерируемых колебаний  и полный к. п. д. (). Ко второй группе относятся зависимости генерируемой мощности и частоты от полного сопротивления (полной проводимости) нагрузки.

Вольтамперные характеристики магнетрона, снятые при условиях В = const, Р_ген = const,  = const или  = const, носят название рабочих характеристик. Эти характеристики принято строить в прямоугольной системе координат, по вертикальной оси которой откладывается постоянное анодное напряжение, а по горизонтальной оси — постоянный анодный ток магнетрона.

Нагрузочные характеристики  и  при , как и для других типов автогенераторов СВЧ, удобно строить на комплексной плоскости полного сопротивления нагрузки в полярной системе координат.

Расчета нагрузочных и рабочих характеристик магнетронов обычно не производят. Тем не менее, форма этих характеристик непосредственно обусловливается физическими процессами, происходящими в магнетроне, и может быть качественно получена из простых соображений.

Рассмотрим идеализированные рабочие характеристики, которые можно предположить, если исходить из описанных свойств магнетронов типа бегущей волны.

Семейство кривых постоянной генерируемой мощности Р_ген = const можно получить из следующих соображений. Генерируемая мощность магнетрона, как и всякого электронного прибора, связана с постоянным анодным напряжением, постоянным анодным током и к. п. д. соотношением . Его можно переписать в виде

.

Отсюда следует, что если бы к. п. д. магнетрона оставался неизменным и не зависел от , то при Р_ген = const вольтамперные-характеристики  имели бы вид равнобочных гипербол. Однако с ростом  электронный к. п. д. несколько уменьшается, так как при этом повышается амплитуда СВЧ колебаний и увеличивается доля мощности, рассеиваемой на аноде в конце последнего витка циклоидальной траектории. Поскольку к. п. д. резонаторной системы, естественно, остается неизменным, то с увеличением тока линии постоянной мощности отклоняются от гипербол и несколько поднимаются, как показано качественно на рис. 1.5.

Чем больше генерируемая мощность, тем выше и правее должны располагаться кривые Р_ген = const.

Рисунок 1.5 - Идеализированные рабочие характеристики магнетронного генератора

Таким образом, вольтамперные характеристики магнетрона при В = const имеют вид семейства кривых с круто возрастающим начальным участком, показанным пунктиром на рис. 1.5, б. Далее следуют излом и почти горизонтальный участок, имеющий небольшой наклон к оси абсцисс и характеризующий работу магнетрона в генераторном режиме.

Типичные рабочие характеристики импульсного магнетрона 10-см диапазона приведены на рис. 1.6. Кроме кривых Р_ген = const и В = const, на этом графике показаны семейства кривых постоянного к. п. д. и постоянной генерируемой частоты. Рабочая точка магнетрона лежит в верхнем правом углу рассматриваемого графика.

Из рисунка 1.6 видно, что опытные кривые хорошо согласуются с обсуждавшимися ранее идеализированными характеристиками. Такое совпадение может рассматриваться как подтверждение правильности сделанных основных качественных предположений о механизме работы магнетрона.

По своему характеру нагрузочные характеристики магнетронов сходны с нагрузочными характеристиками других автогенераторов СВЧ с резонансной колебательной системой, например, отражательных клистронов. Такое сходство обусловлено тем, что затягивание частоты под действием внешней нагрузки обычно значительно меньше разделения видов.

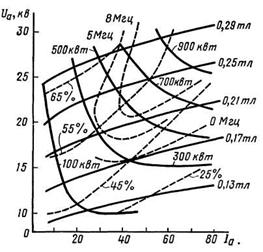
Рисунок 1.6 - Типичные рабочие характеристики импульсного магнетрона 10-см диапазона

В качестве фиксированных параметров при определении нагрузочных характеристик магнетрона выбираются номинальные значения магнитной индукции В и постоянного анодного тока . Иногда (при особенно высокой мощности) во избежание пробоев при больших значениях коэффициента стоячей волны снятие нагрузочных характеристик производится при пониженной мощности. В качестве начала отсчета фазы стоячей волны обычно выбирается выходной фланец магнетрона.

Типичная нагрузочная характеристика импульсного магнетрона 3-см диапазона приведена на рисунке 1.7. Линии постоянной генерируемой мощности близки к окружностям постоянной активной проводимости нагрузки. Линии постоянной частоты имеют веерообразное расположение и близки к линиям постоянной реактивной проводимости на круговой диаграмме полных проводимостей в полярной системе координат.

Важным параметром магнетронов является степень затягивания частоты, определяемая при коэффициенте стоячей волны, равном 1,5(см. рис. 1.7).

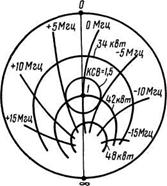
Рисунок 1.7 - Пример реальной нагрузочной характеристики импульсного магнетрона 3-см диапазона

Этот параметр, встречающийся при рассмотрении любого автогенератора СВЧ, приобретает в случае магнетронов особую актуальность, так как магнетроны часто связываются с нагрузкой без развязывающих ослабителей. Обычно степень затягивания F₃для магнетронов 10-см диапазона составляет 10—15 Мгц; в 3-см диапазоне степень затягивания может доходить до 15—20 Мгц. Допустимая степень затягивания находится в тесной связи с возможностями схемы автоматической подстройки частоты, использующей электронную настройку гетеродина — отражательного клистрона.

Основываясь на общих уравнениях затягивания частоты, можно найти соответствующие значения внешней добротности магнетрона на рабочем виде колебаний.

 (1.17)

Через v₀ здесь обозначена генерируемая частота при согласованной нагрузке, примерно равная резонансной частоте "холодного" блока на рабочем виде колебаний. Обычно учитывается также, что линии Р_ген = const и  = const на рис. 1.7 пересекаются под углом, отличным от . В этом случае в правой части уравнения (1.17) вводится дополнительный эмпирический множитель, равный приблизительно 1,05.

Вычислим для примера требующуюся внешнюю добротность магнетрона, предназначенного для работы на волне 3,2 см. Задаваясь допустимой степенью затягивания, равной 20 Мгц, получаем по (1.17) : . Именно такие и несколько более высокие значения типичны для современных магнетронов.

1.5 Конструирования магнетронов

Основными конструктивными узлами современных магнетронов являются:

1) анодный блок (корпус) магнетрона, включающий резонаторную систему и устройства для разделения видов колебаний;

2) система перестройки частоты;

3) вывод энергии;

4) катод с соответствующими выводами;

5) вакуумная оболочка и система охлаждения;

6) магнитная цепь.

В большинстве магнетронов вся резонаторная система, механизм перестройки и значительная часть вывода энергии находятся внутри вакуумной оболочки и являются неотъемлемыми частями магнетрона. Это оказывает большое влияние на конструктивное оформление каждого из указанных узлов магнетрона.

Большинство современных магнетронов, за исключением некоторых магнетронов миллиметрового диапазона, используют p-вид колебаний резонаторной системы. Данный вид колебаний обладает рядом особенностей и преимуществ в сравнении с другими видами колебаний. К числу таких преимуществ относятся отсутствие вырождения, наименьшее анодное напряжение при одной и той же индукции магнитного поля (если отвлечься от возбуждения на пространственных гармониках других видов колебаний), а также наибольший к. п. д. при неизменной величине магнитной индукции. Достоинством p-вида является также конструктивная простота требующихся для этого резонансных систем.

При выборе количества резонаторов N необходимо учитывать следующее. Прежде всего, число N должно быть четным, чтобы обеспечить существование p-вида колебаний. Увеличение числа резонаторов приводит к ухудшению разделения видов колебаний, но одновременно способствует снижению анодного напряжения при заданной индукции В и при неизменном диаметре анода. Обычные магнетроны 10-см диапазона имеют 8—12 резонаторов; в 3-см диапазоне применяются от 12 до 18 резонаторов. При переходе к миллиметровому диапазону число N доходит до 24—38 и более. Несколько особняком стоят коаксиальные магнетроны (см. далее), допускающие использование значительно большего числа резонаторов.

На волнах длиннее 3 смосновное применение находят резонаторы типа щель—отверстие и лопаточные (секторные) резонаторы, показанные на рисунке 1.8. В миллиметровом диапазоне волн часто применяются щелевые резонаторы (рис. 1.8, в).

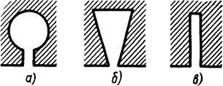
Рисунок 1.8 - Наиболее распространенные типы магнетронных резонаторов

Опыт показывает, что при использовании связок максимальные значения диаметра анодного отверстия d_aи рабочей длины анода . связаны с длиной волны ориентировочными соотношениями

В случае разнорезонаторной системы максимальные величины  и  могут быть заметно повышены:

В миллиметровом диапазоне волн и при идут на увеличение до 1,5 и даже до 2,0. Чтобы избежать при этом резкого увеличения числа резонаторов или повышения анодного напряжения и магнитной индукции, целесообразно использовать работу магнетрона на виде колебаний, отличном от p, при синхронизме с пространственной гармоникой р = +1 или р = —1.

Равнорезонаторные блоки с "многоэтажными" связками, расположенными через равные интервалы по длине анода, могут иметь очень большую длину (до ), что позволяет значительно увеличить длину катода и резко повысить генерируемую мощность.

Механическая перестройка (настройка) частоты основывается на изменении резонансной частоты p-вида колебаний анодного блока. Существование нескольких близко расположенных по частоте видов колебаний осложняет механическую настройку магнетронов. Важными условиями при любом способе перестройки являются сохранение достаточного разделения видов и приблизительное постоянство собственной и нагруженной добротностей анодного блока в пределах рабочего диапазона частот. Всякие паразитные резонансы, кроме основного резонанса p-вида, являются недопустимыми.

Наиболее распространен вариант симметричной механической перестройки. Одновременное воздействие на резонаторы производится индуктивным или емкостным способом с помощью металлических колец, стержней и коронок, перемещающихся внутри резонаторов или в торцевых пространствах магнетрона. Несколько систем, обеспечивающих диапазон перестройки до ± (3¸6) % от средней частоты, показаны схематически на рис. 1.9. При настройке индуктивным кольцом (рис. 1.9, а) основное воздействие производится на высокочастотное магнитное поле, проходящее через торцевое пространство. С приближением металлического кольца к торцу анодного блока уменьшается эквивалентная индуктивность всех резонаторов и, как следствие, повышается резонансная частота каждого резонатора и всего анодного блока в целом. Воздействие на высокочастотное магнитное поле в самих резонаторах производится с помощью индуктивной коронки, имеющей металлические стержни, как показано на рис. 1.9, б. Похожим образом производится емкостная настройка магнетрона, при которой металлическое кольцо или коронка (см. рис. 1.9, в, г) перемещается в торцевом пространстве вблизи той части сегментов, где имеется наиболее сильное электрическое поле, или около связок. Для расширения диапазона иногда используют комбинацию емкостной и индуктивной перестроек.

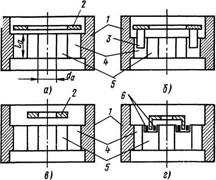
Рисунок. 1.9 - Симметричная механическая настройка магнетрона индуктивным кольцом и индуктивной коронкой (а, б) и емкостнымикольцом и коронкой (в, г):1- анодный блок; 2- металлическое кольцо; 3- металлический стержень; 4 -отверстие резонатора; 5 - щель рез