Скачать

Показатели эконометрики

Эконометрика – наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов..

Этапами эконометрических исследований являются:

- постановка проблемы;

- получение данных, анализ их качества;

- спецификация модели;

- оценка параметров;

- интерпретация результатов.

Эконометрическое исследование включает решение следующих проблем:

- качественный анализ связей экономических переменных – выделение зависимых и независимых переменных;

- подбор данных;

- спецификация формы связи между у и х;

- оценка параметров модели;

- проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты;

- анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление переменных, ответственных за мультиколлинеарность;

- введение фиктивных переменных;

- выявление автокорреляции, лагов;

- выявление тренда, циклической и случайной компонент;

- проверка остатков на гетероскедатичность;

- и др.

Целью данной контрольной работы является приобретение умения построения эконометрических моделей, принятие решений о спецификации и идентификации моделей, выбор метода оценки параметров модели, интерпретация результатов, получение прогнозных оценок.

Задачей данной работы является решение поставленных вопросов с помощью эконометрических методов. Данная работа позволит приобрести навыки использования различных эконометрических методов.

Задача 1

По данным, представленным в таблице выполнить следующие расчеты:

1. рассчитать параметры парной линейной регрессии.

2. оценить тесноту связи с помощью показателей корреляции и детерминации

3. оценить с помощью средней ошибки аппроксимации качество уравнений.

4. оценить статистическую зависимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдентов

5. рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 20% от его среднего уровня значимости α = 0,05

Решение.

Рассчитаем параметры парной линейной регрессии. Для этого выберем модель уравнения, построим уравнение тренда.

Для рассмотрения зависимости урожайности от дозы внесенных удобрений используем уравнение прямой:

y = a + bx

где х – независимый признак, доза внесенных удобрений

у – урожайность,

a, b – параметры уравнения регрессии.

Для расчетов параметров уравнения составим систему уравнений

na + ∑х = ∑у

a∑х + ∑х² = ∑ух

где n – число наблюдений, n=25

25а +86,5 = 256,9

86,5a + 844,941 = 995,969

Параметры а и b можно определить по формулам

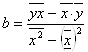 и a = y - bx

= (39,839 – 3,46∙10,276)/ (33,798-3,46²) = 0,1960

а = 10,276 – 0,196∙3,46 = 9,598

ỹ = 9,598 + 0,196х

Коэффициент регрессии b= 0,196 ц/га показывает, насколько в среднем повысится урожайность при увеличении дозы внесения удобрений на 1 кг.      

Средняя ошибка аппроксимации

= 1/25 ∙494,486 = 19,780%

Ошибка аппроксимации 19,78 % > 12% – модель ненадежна и статистически незначима.

Оценим тесноту связи с помощью показателей корреляции и детерминации.

Тесноту связи показывает коэффициент корреляции:

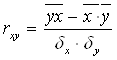
δ_x- показывает, что в среднем фактор Х меняется в пределах

, 3,46 ± 4,672

δ_у - показывает, что в среднем фактор Y меняется в пределах

, 10,276 ± 2,289

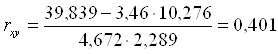
r_xy = 0,401, 0,3≤0,401≤0,5 – связь слабая

Коэффициент детерминации R = r_xy² ∙100% = 0,401²∙100% = 16,08.

yзависит от выбранного x на 16,08%, на оставшиеся 100-16,08% y зависит от других факторов.

Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

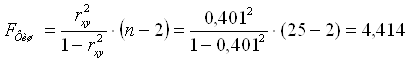
При α = 0,05, κ₁ = n-1, κ₂ = n-2 =25-2 =23

F_табл. = 2,00, F_Фиш. = 4,414 > F_табл. = 2,00 – модель значима и надежна

Рассчитаем прогнозное значение результата с вероятностью 0,95% при повышении дозы внесения удобрений от своего среднего уровня и определим доверительный интервал прогноза.

Найдем точечный прогноз для х_{прогноз} = 1,2∙х , х_р = 1,2 ∙3,46 = 4,152

ỹ = a+bx, ỹ_р = 9,598 + 0,196∙ х_р = 9,598 + 0,196∙4,152 = 10,412

Найдем среднюю ошибку прогнозного значения

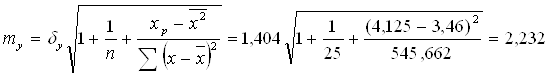
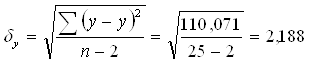
F_табл. Стьюдента для α = 0,05, df = n-2 = 25-2 = 23

t_табл.=2,0687,

∆_ур = t_табл∙станд.ошибка = 2,0687∙2,188 = 4,526

Доверительный интервал прогноза по урожайности

γ_ур = y_p± ∆_ур = 10,412 ± 4,526, от 5,886 до 14,938