Скачать

Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки

Глава 1. Цель исследования

Глава 2. Методика исследования данной работы

Глава 3. Результаты исследования и их практическая значимость

Список использованной литературы

Приложение

Введение

Основная цель при решении систем линейных уравнений - решить систему уравнений, то есть найти все ее решения или доказать, что решений нет. Для решения системы уравнений с двумя переменными используются:

1-графический способ,

2. способ подстановки,

3 - способ сложения.

Практическое применение этих способов - это решение задач, по алгебре, физике, химии, геометрии.

1 - Кроме этого умение определить без построения графиков число решений системы линейных уравнений с числовыми коэффициентами. Основная цель, которая ставится при изучении темы - понять, то, что вопрос о числе решений системы двух линейных уравнений (если исключить выраженный случай а=0, в=0 для линейного уравнения ах + ву = с) сводиться к определению числа общих точек прямых, являющимися графиками уравнений системы.

Известно, что графиком линейного уравнения является прямая.

Рассмотрим три случая расположения прямой.

Случай 1.

Прямые, являющиеся графиком уравнения, входящих в эту систему, пересекаются. Решим систему уравнений:

Уравнениями у = - 1, Iх + 12 и у = - 6х + 18 задаются линейные функции. Угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит, эти прямые пересекаются, и система имеет единственное решение. Прировняв правые части уравнений, найдем точку пересечения Данная система имеет единственное решение: пара чисел.

Случай 2.

Прямые, являющиеся графиками уравнений системы, параллельны. Решим систему уравнений:

Прямые, являющиеся графиками линейных функций у = - О,4х+О,15 и

У = - О,4х+3,2, параллельны, так как их угловые коэффициенты одинаковы, а точки пересечения с осью у различны. Отсюда следует, что данная система уравнений не имеет решений

Случай 3.

Прямые, являющиеся графиками уравнений системы, совпадают.

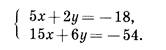
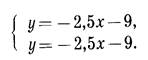
Очевидно, что графики уравнений совпадают. Это означает, что любая пара чисел (х; у), в которой х - произвольное число, а у = - 2,5х - 9, является решением системы. Система имеет бесконечно много решений.

Главная проблема при решении системы линейных уравнений графическим способом у учащихся это?

не умения, выражать одну переменную через другую.

не правильное построение системы координат (различный единичный отрезок на осях ординат и абсцисс).

Рассмотрим способ решения систем линейных уравнений с двумя переменными, называемый способом подстановки. Начнем с задачи.

Ученик задумал два числа. Первое число на 7 больше второго. Если от утроенного первого числа вычесть удвоенное второе число, то получится 27 Какие числа задумал ученик?

Решение: Пусть х - первое число, у - второе число. По условию задачи составим систему уравнений.

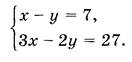
В первом уравнении выразим х через у: х = у + 7.

Подставив во второе уравнение вместо переменной х выражение х = у + 7, получим систему

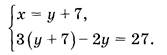
Второе уравнение системы представляет собой уравнение с одной переменной.

Решим его:

Зу+2I-2у=27; у=6.

Подставив в первое уравнение системы вместо переменной у ее значение, равное 6, получим:

х=6+ 7;

х= 13.

Пара чисел (13;

6) является решением системы. Ответ: (13;

6).

Главная проблема при решении системы линейных уравнений способом подстановки у учащихся это?

не умения, выражать одну переменную через другую.

не умение, подставить уже полученную переменную (не видят)

Рассмотрим еще один способ решения систем линейных уравнений - способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Решим систему уравнений:

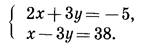
В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почтенно левые и правые части уравнений, получим уравнение с одной переменной:

3х = 33.

Заменим одно из уравнений системы (1), например первое, уравнением 3х=33. Получим систему:

Система (2) равносильна системе (1). Решим систему (2). Из уравнения 3х=33 находим, что х=11. Подставив это значение х в уравнение х-3у=38, получим уравнение с переменной у:

Решим это уравнение:

II-Зу=38.

3у=27,у= - -9.

Пара (11; - 9) - решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели ее решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2х+3у= - 5 и х-3у=38 пересекаются.

Главная проблема при решении системы линейных уравнений способом подстановки у учащихся это?

1) не умение, подставить уже полученную переменную (не видят)

Проанализировав основные проблемы решение линейных систем уравнений с двумя переменными, можно сделать вывод:

Главная проблема при решении систем линейных уравнений различными способами у учащихся это?

не умения, выражать одну переменную через другую. (в трех случаях)

не умение, подставить уже полученную переменную (в двух случаях)

И обе эти проблемы встречаются при решении линейных систем уравнений способом подстановки.

Почему я решил проводить исследование в этой области?

Проанализировав основные проблемы решение линейных систем уравнений с двумя переменными, можно сделать вывод.

Главная проблема при решении систем линейных уравнений различными способами у учащихся это?

не умения, выражать одну переменную через другую. (в трех случаях)

не умение, подставить уже полученную переменную (в двух случаях)

И обе эти проблемы встречаются при решении линейных систем уравнений способом подстановки.

Кроме этого, решение задач составлением систем уравнений, по физике, алгебре, геометрии и химии для таких учащихся останутся недоступными. Поэтому я решил, заняться, поиском более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки.

Я считаю, что моя работа, в этом направлении очень актуальна.

Глава 1. Цель исследования

1. Найти более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки.

Из истории решения системы уравнений, содержащей одно уравнение второй степени и одно линейное в древневавилонских текстах, написанных в III-II тысячелетиях до н.э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени.

Задача 1 “Площади двух своих квадратов я сложил: . Сторона второго квадрата равна стороны первого и еще 5".

Соответствующая система уравнений в современной записи имеет вид:

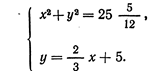
Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат и согласно формуле квадрата суммы, которая ему, видимо, была известна, получает:

Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:

Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.

Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики".

Задача 2. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов - 208".

Эту задачу мы решили бы путем составления системы уравнений:

Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):

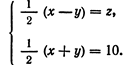
Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем

x = 2 + 10; у = 10 - 2. Далее, х² + у² = (г +lO) ² + (10 - г) ² == 2z² + 200.

Таким образом,

2z² + 200 = 208,

Откуда

z = 2; х = 2 + 10 = 12; у = 10 - 2 = 8.

В поисках различных решений я обнаружил следующее.

Основные методы решения рациональных уравнений.

1) Простейшие: решаются путём обычных упрощений - приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax² + bx + c = 0 решаются по выведенной нами формуле

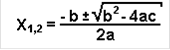
Также используется теорема Виета:

x₁ + x₂ = - b / a; x₁x₂ = c / a.

2) Группировка: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа - ноль. Затем приравниваем к нулю каждый из сомножителей.

3) Подстановка: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно что удобно обозначить. Например, уравнение (x² + x - 5) / x + 3x / (x² + x - 5) + 4 = 0,легко решается с помощью подстановки (x² + x - 5) / x = t, получаем t + (3/t) + 4 = 0. Или: 21/ (x² - 4x + 10) - x² + 4x = 6. Здесь можно сделать подстановку x² - 4 = t. Тогда 21/ (t + 10) - t = 6 и т.д.

В более сложных случаях подстановка видна лишь после нескольких преобразований. Например, дано уравнение

(x² + 2x) ² - (x +1) ² = 55.

Переписав его иначе, а именно (x² + 2x) ² - (x² + 2x + 1) = 55, сразу увидим подстановку x² + 2x=t.

Имеем t² - t - 56 = 0, t₁ = - 7, t₂ = 8. Осталось решить x² + 2x = - 7 и x² + 2x = 8. В ряде других случаев удобную подстановку желательно знать “заранее". Например

1) Уравнение (x + a) ⁴ + (x + b) ⁴ = c сводится к биквадратному, если сделать подстановку

x = t - (a + b) / 2.

2) Симметрическое уравнение (возвратное) a₀xⁿ + a₁x^{n - 1} + … + a₁x + a₀ = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1/x = t, если n - чётное; если n - нечётное, то уравнение имеет корень x = - 1.

3) Уравнение вида (x + a) (x + b) (x + c) (x + d) = l сводится к квадратному, если a + b = c + d и т.д.

4) Подбор: при решении уравнений высших степеней рациональные корни уравнения a_nxⁿ + a_{n - 1}x^{n - 1} + …+ a₁x + a₀ = 0 ищем в виде p / q, где p - делитель a₀, q - делитель a_n, p и q взаимно просты, pÎZ, qÎN.

5) “Искусство”, т.е. решать пример нестандартно, придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.

6) Уравнения с модулем: при решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что

f (x), если f (x) ³ 0,| f (x) | =

f (x), если f (x) < 0.

Это уже изученные методы и широко применяемые в практической математике. Выделенные жирным курсивом - это методы мною изучаемые 5) “Искусство", - это то, что мне предстоит найти.

Хотелось бы остановится на некоторых из них.

Метод Гаусса.

Пусть дана система линейных уравнений

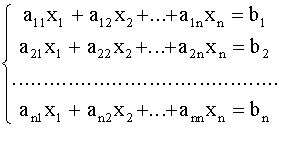(1)

Коэффициенты a _11,12,..., a _1n,..., a _n1, b _2,..., b _n считаются заданными. Вектор - строка í x _1, x _2,..., x _n ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.

Определитель n-го порядка D = ç A ê = ç a _ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.

a). Если D ¹ 0, то система (1) имеет единственное решение, которое может быть найдено методом ГАУССА. б). Если D = 0, то система (1) либо имеет бесконечное множество решений, либо несовместна, т.е. решений нет.

1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

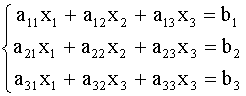(2).

Метод Гаусса решения системы (2) состоит в следующем: Разделим все члены первого уравнения на , а затем, умножив полученное уравнение на , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное будет исключено, и получиться система вида:

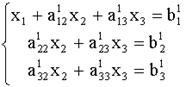(3)

Теперь разделим второе уравнение системы (3) на , умножим полученное уравнение на и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное будет исключено и получиться система треугольного вида:

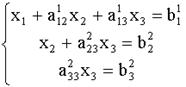(4)

Из последнего уравнения системы (4) находим , подставляя найденное

подставляя найденное значение в первое уравнение, находим .

Методом Гаусса решить систему:

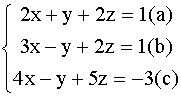
Решение: Разделив уравнение (а) на 2, получим систему

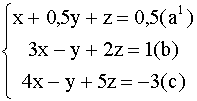
Вычтем из уравнения (b) уравнение , умноженное на 3, а из уравнения (c) - уравнение , умноженное на 4.

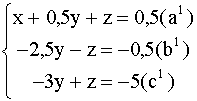
Разделив уравнение () на - 2,5, получим:

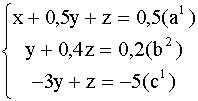
Вычтем из уравнения () уравнение , умноженное на - 3:

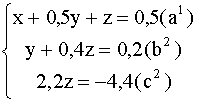
Из уравнения находим Z=-2; подставив это значение в уравнение , получим Y=0,2-0,4Z=0,2-0,4 (-2) =1; наконец, подставив значение Z=-2 и Y=1 в уравнение (a ¹⁾, находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2) =2. Итак, получаем ответ X=2, Y=1, Z=-2.

Проверка:

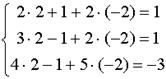
Линейные уравнения.

Уравнения вида ax+b=0, где a и b - некоторые постоянные, называется линейным уравнением.

Если a¹0, то линейное уравнение имеет единственный корень: x = - b /a.

Если a=0; b¹0, то линейное уравнение решений не имеет.

Если a=0; b=0, то, переписав исходное уравнение в виде ax = - b, легко видеть, что любое x является решением линейного уравнения.

Уравнение прямой имеет вид: y = ax + b.

Если прямая проходит через точку с координатами X₀ и Y₀, то эти координаты удовлетворяют уравнению прямой, т.е. Y₀ = aX₀ + b.

Пример 1.1 Решить уравнение

2x - 3 + 4 (x - 1) = 5.

Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x - 3 + 4x - 4 = 5, 2x + 4x = 5 + 4 + 3,6x = 12, x = 2.

Ответ: 2.

Пример 1.2 Решить уравнение 2x - 3 + 2 (x - 1) = 4 (x - 1) - 7.

Решение.2x + 2x - 4x = 3 +2 - 4 - 7, 0x = - 6.

Ответ: Æ.

Пример 1.3 Решить уравнение.

2x + 3 - 6 (x - 1) = 4 (x - 1) + 5.

Решение.

2x - 6x + 3 + 6 = 4 - 4x + 5,- 4x + 9 = 9 - 4x,

4x + 4x = 9 - 9,0x = 0.

Ответ: Любое число.

Системы линейных уравнений.

Уравнение вида

a₁x₁ + a₂x₂ + … + a_nx_n = b,

где a₁, b₁, …,a_n, b - некоторые постоянные, называется линейным уравнением с n неизвестными x₁, x₂, …, x_n.

Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n неизвестных, то возможны следующие три случая:

система не имеет решений;

система имеет ровно одно решение;

система имеет бесконечно много решений.

Пример: решить систему уравнений

x + y - z = 2,2

x - y + 4z = 1,

x + 6y + z = 5.

Решение. При решении систем линейных уравнений удобно пользоваться методом Гаусса, который состоит в преобразовании системы к треугольному виду.

Умножаем первое уравнение системы на - 2 и, складывая полученный результат со вторым уравнением, получаем - 3y + 6z = - 3. Это уравнение можно переписать в виде y - 2z = 1. Складывая первое уравнение с третьим, получаем 7y = 7, или y = 1.

Таким образом, система приобрела треугольный вид

x + y - z = 2,

y - 2z = 1 ,y = 1.

Подставляя y = 1 во второе уравнение, находим z = 0. Подставляя y =1 и z = 0 в первое уравнение, находим x = 1.

Ответ: (1; 1; 0).

Системы уравнений второй степени.

В простейших случаях при решении систем уравнений второй степени удаётся выразить одно неизвестное через другое и подставить это выражение во второе уравнение.

При решении систем уравнений второй степени часто используется также способ замены переменных.

Пример. Среди решений (x; y) системы найти то, для которого сумма (x + y) максимальна. Вычислить значение этой суммы.

2x + y = 7,

xy = 6.

Решение. Из первого уравнения получаем y = 7 - 2x. Подставляя значение y во второе уравнение, получаем систему уравнений

y = 7 - 2x,

7x - 2x² = 6.

Квадратное уравнение - 2x² + 7x - 6 = 0 имеет корни X1 = 2; X2 = 3/2. Из первого уравнения получаем Y1 = 3; Y2 = 4.

Решения имеют вид (2;3) и (1,5;4). Наибольшая сумма x + y = 1,5 + 4 = 5,5.

Ответ: 5,5.

Метод введения новых неизвестных при решении уравнений и систем уравнений.

При решении биквадратных и возвратных уравнений мы вводили новые неизвестные (у = х² для биквадратных уравнений и у = х + 1/х для возвратных уравнений). Введение новых неизвестных применяется также при решении уравнений иного вида и систем уравнений.

Пример Решим уравнение 12/ (х² + 2х) - 3/ (х² + 2х - 2) = 1.

Решение. Если попробовать привести дробь в левой части уравнения к одному знаменателю, то получим уравнение четвёртой степени, которое мы умеем решать.

Чтобы решить заданное уравнение, заметим, что в обе дроби входит одно и то же выражение х² + 2х. Поэтому введём новое неизвестное у, положив, что у = х² + 2х. Тогда уравнение примет вид

12/у - 3/ (у - 2) = 1 или (у² - 11у + 24) / (у (у - 2)) = 0,откуда y₁ = 3; y₂ = 8. Осталось решить уравнения х² + 2х = 3 (его корни х₁ = 1, х₂ = -3) и х² + 2х = 8 (его корни х₃ = 2, х₄ = -4).

Применённый метод называется методом введения новых неизвестных, и его полезно применять, когда неизвестное входит в уравнение всюду в виде одной и той же комбинации (особенно если эта комбинация содержит степени неизвестного выше первой).

Пример. Решим систему уравнений

2/х + 3/у = 8,5

/х - 2/у = 1.

Решение.

Обозначим 1/х через U, а 1/у через V.

Тогда система примет вид

2U + 3V = 8,5

U - 2V = 1,

т.е. получится система двух линейных уравнений с двумя неизвестными U и V. Из первого уравнения выражаем U через V: U = 4 - 3V / 2, и подставляя во второе: 5 (4 - 3V / 2) -2V = 1, откуда V = 2. Теперь находим U = 1 и решаем уравнения 1/x = 1, 1/y = 2.

Ответ: x = 1, y = 0,5.

Однородные уравнения.

Пример Решим систему уравнений

8х² - 6ху + у2 = 0,

х² + у² = 5.

Решение. заметим, что для решения системы выполняется условие у ¹ 0. В самом деле, из первого уравнения следует, что если у = 0, то и х = 0, а числа х = 0 и у = 0 не удовлетворяют второму уравнению системы. Разделим первое уравнение на у².

Получится уравнение

8х^2/у² - 6ху / у² + у^2/у² = 0 или

8х^2/у² - 6х / у + 1 = 0.

Введём вспомогательное неизвестное U = х / у.

Уравнение примет вид

8U² - 6U + 1 = 0.

Это квадратное уравнение, имеющее корни U₁ = 0,5; U₂ = 0,25. Таким образом, из первого уравнения мы получаем что либо x / y = 1/2, либо x / y = 1/4. Осталось подставить выражения у =2х и у = 4х (рассмотрев оба случая) во второе уравнение системы. В первом случае получается уравнение 5х² = 5, откуда х₁ = 1, х₂ = - 1; соответственно у₁ = 2, у₂ = - 2.

Во втором случае получается уравнение17х² = 5, откуда х₃ = Ö (5/17), x₄ = -Ö (5/17); соответственно y₃ = 4Ö (5/17), y₄ = - 4Ö (5 /17).

Первое уравнение системы нам удалось представить как уравнение относительно x / y благодаря тому, что степень всех членов, входящих слагаемыми в это уравнение (8x², 6xy, y²), одна и та же - она равна двум. Поэтому после деления на y² каждое слагаемое выразилось через x / y.

Многочлен от двух переменных x и y такой, что степень каждого его члена равна одному и тому же числу k, называется однородным многочленом степени k.

Уравнение вида P (x, y) = 0 называется однородным уравнением степени k относительно x и y, если P (x, y) - однородный многочлен степени k. Однородное уравнение относительно x и y делением на y^{k (}если y = 0 не является корнем уравнения) превращается в уравнение относительно неизвестного x / y. Это свойство однородного уравнения помогает решать многие задачи.

Решение симметрических систем уравнений.

Напомним, что многочлен P (x, y) называется симметрическим, если P (x, y) = P (y, x).

При решении систем уравнений вида

P₁ (x, y) = 0,

P₂ (x, y) = 0,

где P₁ (x, y) и P₂ (x, y) - симметрические многочлены, полезной оказывается такая замена неизвестных: x + y = U, xy = V. Напомним, что любой симметрический многочлен P (x, y) можно представить как выражение от U и V.

Пример Решить систему уравнений

x² + xy + y² = 49,

x + y + xy = 23.

Решение. Заметим, что:

x² + xy + y² = x² + 2xy + y² - x

y = (x + y) ² - xy.

Сделаем замену неизвестных: x + y = U, xy =V.

Система примет вид:

U² - V = 49,

U + V = 23.

Сложив эти уравнения, получим уравнение U² + U - 72 = 0 с корнями U₁ = 8,U₂ = -9. Соответственно V₁ = 15, V₂ = 32. Остаётся решить системы уравнений:

x + y = 8,xy = 15,

x + y = - 9,xy = 32.

Система x + y = 8, имеет решения:

x₁ = 3, y₁ = 5; x₂ = 5,

y₂ = 3.xy = 15.

Система x + y = - 9, действительных решений не имеет. Ответ: x₁ = 3, y₁ = 5; x₂ = 5, y₂ = 3.

Глава 2. Методика исследования данной работы

Методика исследовании.

Моя основная цель, найти более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки.

Поэтому я решил использовать метод “Искусство", т.е. решать примеры нестандартно, придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.

При решении систем уравнений второй степени часто используется также способ замены переменных - его я тоже решил применить.

Итак, для решения проблемы я решил использовать два методы решений:

1. метод "Искусство" - "свой метод"

2. метод замены переменных

Этапы исследования.

Основными методами решения систем являются метод подстановки и метод введения новых переменных.

Предлагается симметрическая система уравнений; стабильная замена переменных

Решение задач:

Старинная задача.

Три сестры пришли на рынок с цыплятами. Одна принесла для продажи 10 цыплят, другая 16, третья 26. До полудня они продали часть своих цыплят по одной и той же цене. После полудня опасаясь,, что не все цыплята будут проданы, они понизили цену и распродали оставшихся цыплят снова по одинаковой цене. Домой все трое вернулись с одинаковой выручкой: каждая сестра получила от продаж 35 рублей.

По какой цене продали они цыплят до и после полудня?

Решение

Обозначим число цыплят проданных каждой сестрой до полудня, через х, у, z. Во вторую половину дня они продали 10 - х, 16 - у, 26 - z. Цену до полудня обозначим через m, после полудня - через n. Для ясности сопоставим эти обозначения.