Парная и множественная регрессия и корреляция
1. Парная линейная регрессия и корреляция
Цель работы - овладеть навыками определения параметров линейной регрессии и корреляции с использованием формул и табличного процессора MS Excel.
1.1 Решение задач с использованием формул
1.1.1 Параметры a и b линейной регрессии
![]()
рассчитываются с помощью метода наименьших квадратов. Для этого составим систему нормальных уравнений (1).
По исходным данным определим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() в расчетной таблице 1.
в расчетной таблице 1.
Таблица 1 Расчет показателей парной линейной регрессии и корреляции
| № |
|
|
|
|
|
|
|
|
|
| 1 | 9.8 | 10.2 | 99.96 | 96.04 | 104.04 | 9.847 | 0.035 | 0.125 | -1.575 |
| 2 | 11.3 | 10.1 | 114.13 | 127.69 | 102.01 | 10.088 | 0.001 | 0.000 | 11.300 |
| 3 | 11.5 | 10.1 | 116.15 | 132.25 | 102.01 | 10.120 | -0.002 | 0.000 | 11.500 |
| 4 | 11.3 | 9.2 | 103.96 | 127.69 | 84.64 | 10.088 | -0.096 | 0.788 | 11.300 |
| 5 | 10.9 | 10.7 | 116.63 | 118.81 | 114.49 | 10.023 | 0.063 | 0.458 | 10.900 |
| 6 | 11.4 | 9 | 102.6 | 129.96 | 81 | 10.104 | -0.123 | 1.218 | 11.400 |
| 7 | 12.6 | 10.4 | 131.04 | 158.76 | 108.16 | 10.297 | 0.010 | 0.011 | 12.409 |
| 8 | 12.2 | 11.1 | 135.42 | 148.84 | 123.21 | 10.232 | 0.078 | 0.753 | 12.164 |
| Итого | 91 | 80.8 | 919.89 | 1040.04 | 819.56 | 80.797 | -0.034 | 3.353 | 79.397 |
| Среднее | 11.375 | 10.1 | 114.986 | 130.005 | 102.445 | 10.100 | -0.004 | ´ | ´ |
Система нормальных уравнений составит:
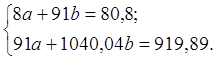
Решив систему, получим: a = 8,2717; b = 0,1607.
Уравнение линейной регрессии имеет вид:
![]() .
.
Параметры уравнения можно определить и по следующим формулам:
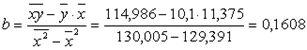
![]() = 10,1 – 0,1608. 11,375= 8,2709
= 10,1 – 0,1608. 11,375= 8,2709
Величина коэффициента регрессии b = 0,1607 означает, что с ростом среднедушевых доходов на 1 тыс. руб. общий коэффициент рождаемости увеличится в среднем на 0,1607 раз.
1.1.2 Средний коэффициент эластичности для линейной регрессии находится по формуле:
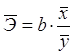
![]() 0,181
0,181
При увеличении величины среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем увеличится на 0,181%.
1.1.3 Линейный коэффициент парной корреляции (r) определяется по формуле:
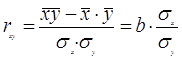 ,
,
где средние квадратические отклонения:
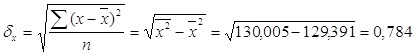
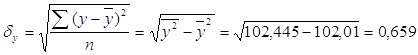
тогда ![]() , значит связь между среднедушевым доходом и рождаемостью очень слабая.
, значит связь между среднедушевым доходом и рождаемостью очень слабая.
1.1.4 Определим коэффициент детерминации:
![]()
Таким образом, вариация величины рождаемости на 3,6% зависит от вариации уровня среднедушевых доходов населения, а на остальные (100%-3,6%) 96,4% − от вариации факторов, не включенных в модель.
Подставляя в уравнение регрессии фактические значения x, определим теоретические (расчетные) значения ![]() (таблица 1) и найдем величину средней ошибки аппроксимации (
(таблица 1) и найдем величину средней ошибки аппроксимации (![]() ):
):
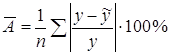 =
=![]() =0,425
=0,425
Так как допустимый предел значений ![]() не более 8-10%, качество модели по данному показателю удовлетворительное. Однако средняя ошибка аппроксимации не является главным критерием оценки значимости модели.
не более 8-10%, качество модели по данному показателю удовлетворительное. Однако средняя ошибка аппроксимации не является главным критерием оценки значимости модели.
С помощью F−критерия Фишера оценим статистическую надежность результатов регрессионного моделирования:
Fфакт=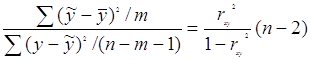 =
=![]() .
.
Fтабл = 5,99 при ![]() .
.
Так как Fфакт < Fтабл, уравнение регрессии не значимо, статистически не надежно.
1.2 Решение задачи с помощью MS Excel
1.2.1 Параметры линейной регрессии
![]()
можно определить с помощью встроенной статистической функции ЛИНЕЙН MS Excel. Порядок вычисления следующий:
1) ввожу исходные данные (рисунок 1).
2) выделяю область пустых ячеек 5´2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии;
3) активизирую Мастер функций любым из способов:
а) в главном меню выбираю Вставка / Функция;
б) на панели инструментов Стандартная щелкаю по кнопке Вставка функции;
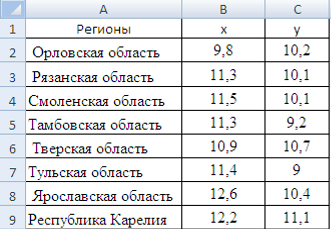
Рисунок 1 Ввод данных для корреляционно-регрессионного анализа
4) в окне «Категория» выбераю Статистические, в окне «Функция» – ЛИНЕЙН. Щелкаю по кнопке ОК (рисунок 2);
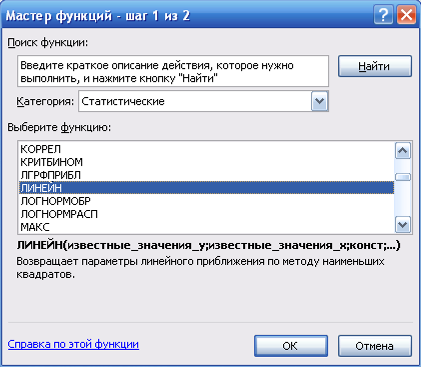
Рисунок 2 Диалоговое окно Мастер функций
5) заполняю аргументы функции (рисунок 3):
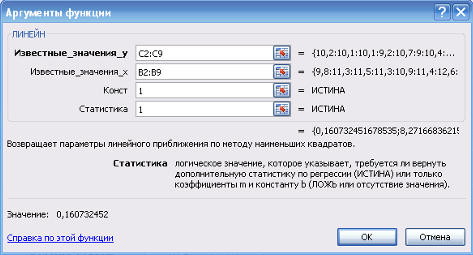
Рисунок 3 Диалоговое окно Аргументы функции
Щелкаю по кнопке ОК;
6) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажимаю на клавишу
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение a |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение y |
| F – статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Результаты вычислений функции ЛИНЕЙН представлены на рисунке 4.
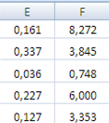
Рисунок 4 Результаты вычислений функции ЛИНЕЙН
1.2.2 С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1) проверяю доступ к пакету анализа. В главном меню последовательно выбераю Сервис / Настройки. Устанавливаю флажок Пакет анализа;
2) в главном меню выбираю Сервис / Анализ данных / Регрессия. Щелкаю по кнопке ОК;
3) после вызова режима Регрессия на экране появляется диалоговое окно (рисунок 5), в котором задаются следующие параметры:
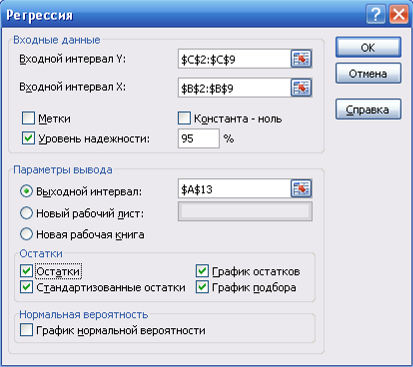
Рисунок 5 Диалоговое окно режима Регрессия
Результаты регрессионного анализа для исходных данных представлены на рисунке 6.
Вывод итогов
| Регрессионная статистика | |
| Множественный R | 0,19101862 |
| R-квадрат | 0,03648811 |
| Нормированный R-квадрат | -0,1240972 |
| Стандартная ошибка | 0,74755394 |
| Наблюдения | 8 |
Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 0,12697864 | 0,126978637 | 0,2272195 | 0,6504571 |
| Остаток | 6 | 3,35302136 | 0,558836894 | ||
| Итого | 7 | 3,48 |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 8,271668362 | 3,844685341 | 2,151455224 | 0,07495556 | 1,135937744 | 17,67927447 |
| Переменная X 1 | 0,160732452 | 0,337194727 | 0,476675461 | 0,6504571 | 0,664353319 | 0,985818223 |
Вывод остатка
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 1 | 9,846846389 | 0,353153611 | 0,510263509 |
| 2 | 10,08794507 | 0,012054934 | 0,017417896 |
| 3 | 10,12009156 | -0,020091556 | -0,029029827 |
| 4 | 10,08794507 | -0,887945066 | -1,28297135 |
| 5 | 10,02365209 | 0,676347915 | 0,977239505 |
| 6 | 10,10401831 | -1,104018311 | -1,595170599 |
| 7 | 10,29689725 | 0,103102747 | 0,148970781 |
| 8 | 10,23260427 | 0,867395727 | 1,253280084 |
2. Нелинейные модели регрессии и их линеаризация
Цель работы: ознакомиться с методикой расчета показателей парной нелинейной регрессии и корреляции, овладеть приемами построения нелинейных регрессионных моделей с помощью MS Exсel.
РЕШЕНИЕ:
2.1.1 Регрессия в виде степенной функции имеет вид:
![]() .
.
Для оценки параметров модели линеаризую (привожу к линейному виду) модель путем логарифмирования: ![]() .
.
Обозначаю lny =Y, lna =A, lnx =X.
Тогда получаю: Y=A+bX.
Для расчетов составляю с помощью MS Excel вспомогательную таблицу, в которой рассчитаю натуральные логарифмы с помощью математической функции LN (рисунок 7).
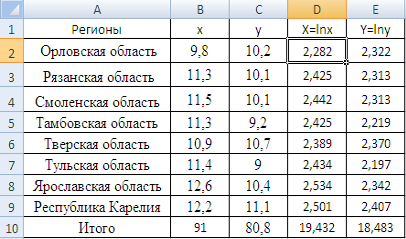
Рисунок 7 Расчет натуральных логарифмов
Далее с помощью инструмента Регрессия рассчитываю параметры уравнения (рисунки 8, 9).
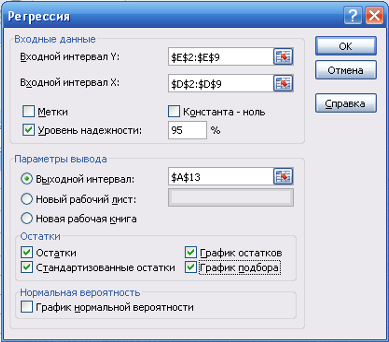
Рисунок 8 Диалоговое окно Регрессия
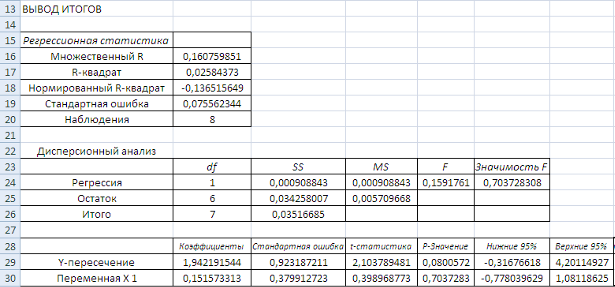
Рисунок 9 Результаты расчета параметров степенной функции
Таким образом, уравнение регрессии имеет вид:
![]() .
.
Выполнив потенцирование, получим:
![]() .
.
Параметр b=0,151 означает коэффициент эластичности, который показывает, что с ростом величины среднедушевых доходов населения на 1% общий коэффициент рождаемости увеличится в среднем на 0,151%.
2.1.2 Регрессия в виде экспоненты имеет вид:
![]() . (13)
. (13)
Для оценки ее параметров необходимо привести уравнение к линейному виду:
![]() .
.
Для расчета параметров экспоненциальной прямой можно воспользоваться статистической функцией ЛГРФПРИБЛ MS Excel. Результаты вычислений представлены на рисунке 10.
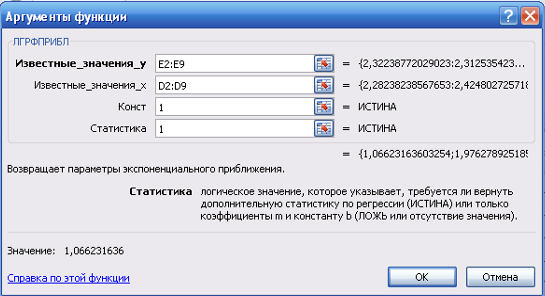
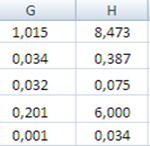
Рисунок 10 Результаты вычислений параметров экспоненциальной функции
Таким образом, уравнение регрессии в виде экспоненты имеет вид:
![]() .
.
2.1.3 Регрессия в виде равносторонней гиперболы имеет вид:
![]() ,
,
чтобы оценить параметры a и b, привожу модель к линейному виду, заменив
![]() .
.
Тогда
![]() .
.
Результаты замены представлены на рисунке 11.
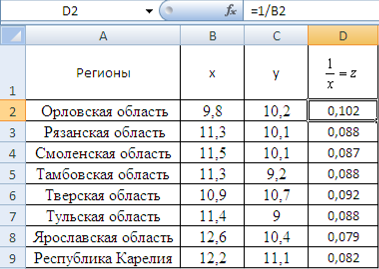
Рисунок 11 Вспомогательная таблица для расчета параметров гиперболы
Далее с помощью инструмента Регрессия рассчитываю параметры уравнения. Результаты расчета представлены на рисунке 12.
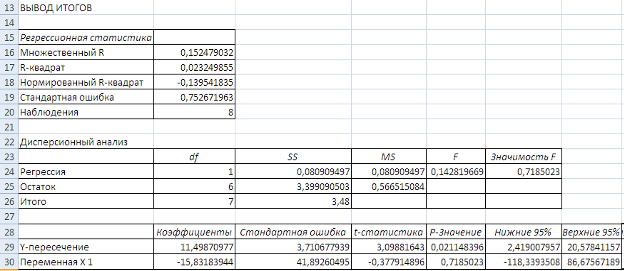
Рисунок 12 Результаты вычислений параметров гиперболической функции
Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице 3.
Все уравнения регрессии достаточно хорошо описывают исходные данные.
Таблица 3 Результаты корреляционно-регрессионного анализа
| Уравнение регрессии | Коэффициент корреляции | Коэффициент детерминации | F-критерий Фишера |
| 0,659 | 0,036 | 0,227 |
| 0,161 | 0,026 | 0,159 |
| 0,179 | 0,032 | 0,201 |
| 0,152 | 0,023 | 0,143 |
Предпочтение можно отдать линейной функции, для которой значения коэффициентов корреляции и детерминации и F-критериев Фишера наибольшие.
3. Множественная регрессия
Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции.
Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости (![]() ) от уровня бедности, % (
) от уровня бедности, % (![]() ) и среднедушевого дохода, тыс. руб. (
) и среднедушевого дохода, тыс. руб. (![]() ).
).
Таблица 1 Исходные данные для корреляционно-регрессионного анализа
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

