Скачать

Основные понятия космической геодезии и астрономии

Искусственные спутники открыли новую эру в науке об измерении Земли — эру космической геодезии.

Они внесли в геодезию новое качество — глобальность; благодаря большим размерам зоны видимости поверхности Земли со спутника значительно упростилось создание геодезической основы для больших территорий, так как существенно сократилось необходимое количество промежуточных этапов измерений. Так, если в классической геодезии среднее расстояние между определяемыми пунктами составляет 10—30 км, то в космической геодезии эти расстояния могут быть на два порядка больше (1—3 тыс. км). Тем самым упрощается передача геодезических данных через водные пространства. Между материком и островами, рифами, архипелагами геодезическая связь может быть установлена при прямой их видимости со спутника непосредственно через него, без каких-либо промежуточных этапов, что способствует более высокой точности построения геодезической сети.

Космическая геодезия – научная дисциплина, в которой для решения научных и практических задач геодезии используются результаты наблюдений искусственных и естественных небесных тел.

В соответствии с этим в предмет изучения в рамках космической геодезии входят:

- Теории движения небесных тел;

- Разработка способов определения орбит небесных тел (прямая задача) и вычисления эфемерид (обратная задача);

- Обоснование требований к геодезическим спутникам в отношении параметров их орбит и состава бортовой аппаратуры;

- Обоснование требований к расположению станций наблюдения и их аппаратурного оснащения;

- изучение методов наблюдений и теории математической обработки наблюдений;

- интерпретация результатов наблюдений и их обработки.

Основными задачами космической геодезии являются:

ü Определение положений и изменений со временем координат наземных пунктов;

ü Изучение внешнего гравитационного поля и его изменений со временем;

ü Уточнение некоторых астрономических постоянных.

При всей глобальности вопросов, охватываемых космической геодезией, автор данной работы поставила перед собой весьма скромную цель:

Рассмотреть основные понятия, без которых дальнейшее углубление в эту науку не представляется возможным.

НЕБЕСНЫЕ КООРДИНАТЫ

При решении задач космической геодезии приходится использовать различные системы координат, отличающиеся между собой:

- расположением начала (например, планетоцентрические, геоцентрические, квазигеоцентрические (референцные) и т.д.;

- ориентированием основной плоскости (например, экваториальные, горизонтальные, орбитальные);

- ориентацией начальной плоскости (например, гринвичские, равноденственные);

- видом координатных систем (прямоугольные, полярные, цилиндрические, и т.д.).

Что же такое небесные координаты и небесная сфера?

Небе́сная сфе́ра — воображаемая вспомогательная сфера произвольного радиуса, на которую проецируются небесные светила: служит для решения различных астрометрических задач. За центр небесной сферы, как правило, принимают глаз наблюдателя. Для находящегося на поверхности Земли наблюдателя вращение небесной сферы воспроизводит суточное движение светил на небе. Площадь небесной сферы с учетом непостоянства значения размеров дуги равных склонений составляет 41252.96 кв. градусов.

Представление о Небесной сфере возникло в глубокой древности; в основу его легло зрительное впечатление о существовании куполообразного небесного свода. Это впечатление связано с тем, что в результате огромной удалённости небесных светил человеческий глаз не в состоянии оценить различия в расстояниях до них, и они представляются одинаково удалёнными. У древних народов это ассоциировалось с наличием реальной сферы, ограничивающей весь мир и несущей на своей поверхности многочисленные звёзды. Таким образом, в их представлении небесная сфера была важнейшим элементом Вселенной. С развитием научных знаний такой взгляд на небесную сферу отпал. Однако заложенная в древности геометрия небесной сферы в результате развития и совершенствования получила современный вид, в котором и используется в астрометрии.

Радиус небесной сферы может быть принят каким угодно: в целях упрощения геометрических соотношений его полагают равным единице. В зависимости от решаемой задачи центр небесной сферы может быть помещен в место:

· где находится наблюдатель (топоцентрическая небесная сфера),

· в центр Земли (геоцентрическая небесная сфера),

· в центр той или иной планеты (планетоцентрическая небесная сфера),

· в центр Солнца (гелиоцентрическая небесная сфера) или в любую др. точку пространства.

Каждому светилу на небесной сфере соответствует точка, в которой её пересекает прямая, соединяющая центр небесной сферы со светилом (с его центром). При изучении взаимного расположения и видимых движений светил на небесной сфере выбирают ту или иную систему координат, определяемую основными точками и линиями. Последние обычно являются большими кругами небесной сферы. Каждый большой круг сферы имеет два полюса, определяющиеся на ней концами диаметра, перпендикулярного к плоскости данного круга.

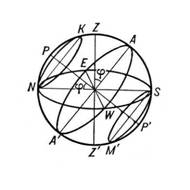
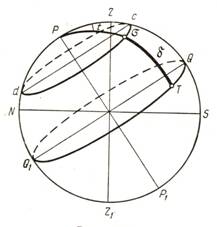
На рисунке изображена небесная сфера, которая соответствует месту наблюдения, расположенному в некоторой точке земной поверхности с широтой f. Отвесная (вертикальная) линия, проведённая через центр этой сферы, пересекает небесную сферу в точках Z и Z', называемых соответственно зенитом и надиром. Плоскость, проходящая через центр небесной сферы перпендикулярно отвесной линии, пересекает сферу по большому кругу NESW, называемому математическим (или истинным) горизонтом. Математический горизонт делит небесную сферу на видимую и невидимую полусферы; в первой находится зенит, во второй — надир. Прямая, проходящая через центр небесной сферы параллельно оси вращения Земли, называемой осью мира, а точки пересечения её с небесной сферой — Северным Р и Южным P' полюсами мира. Плоскость, проходящая через центр небесной сферы перпендикулярно оси мира, пересекает сферу по большому кругу AWA'E, называется небесным экватором. Из построения следует, что угол между осью мира и плоскостью математического горизонта, а также угол между отвесной линией и плоскостью небесного экватора равны географической широте места наблюдений. Большой круг небесной сферы, проходящий через полюсы мира, зенит и надир, называется небесным меридианом.

Из двух точек, в которых небесный меридиан пересекается с математическим горизонтом, ближайшая к Северному полюсу мира N называется точкой севера, а диаметрально противоположная S — точкой юга. Прямая NS, проходящая через эти точки, есть полуденная линия. Точки горизонта, отстоящие на 90° от точек N и S, называются точками востока Е и запада W. Точки N, Е. S, W называются главными точками горизонта. По диаметру EW пересекаются плоскости математического горизонта и небесного экватора.

Большой круг небесной сферы, по которому происходит видимое годичное движение центра Солнца, называется эклиптикой

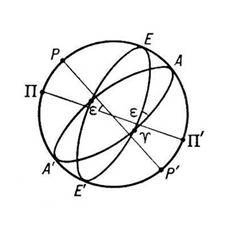
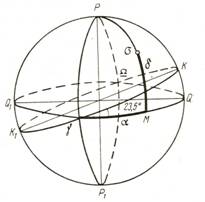
Плоскость эклиптики образует с плоскостью небесного экватора угол e = 23°27'. Эклиптика пересекает экватор в двух точках, одна из которых —точка весеннего равноденствия (в ней Солнце при видимом годичном движении переходит из Южного полушария небесной сферы в Северное), а другая, диаметрально противоположная ей, — точка осеннего равноденствия. Точки эклиптики, отстоящие на 90° от точек весеннего и осеннего равноденствия, называется точками летнего и зимнего солнцестояния (первая — в Северном полушарии небесной сферы, вторая — в Южном). Большой круг небесной сферы, проходящий через полюсы мира и точки равноденствия, называется колюром равноденствий; большой круг небесной сферы, проходящий через полюсы мира и точки солнцестояния, — колюром солнцестояний. Прочерченные на звёздной карте, эти круги отсекают хвосты у древних изображений созвездий Большой Медведицы (колюр равноденствий) и Малой Медведицы (колюр солнцестояний), откуда и происходит их название (греч. kуluroi, буквально — с обрубленным хвостом, от kуlos — обрубленный, отсеченный и ига — хвост).

Видимому суточному перемещению звёзд, являющемуся отображением действительного вращения Земли вокруг оси, соответствует вращение небесной сферы вокруг оси мира с периодом, равным одним звёздным суткам. Вследствие вращения небесной сферы все изображения светил описывают в пространстве параллельные экватору окружности, называются суточными параллелями светил. В зависимости от расположения суточных параллелей относительно горизонта светила подразделяются на незаходящие (суточные параллели располагаются целиком над горизонтом), невосходящие (суточные параллели целиком под горизонтом), восходящие и заходящие (суточные параллели пересекаются горизонтом).

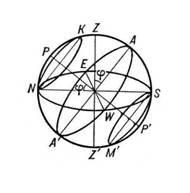
Границами этих групп светил являются параллели KN и SM', касающиеся горизонта в точках N и S . Так как видимость светил определяется положением горизонта, плоскость которого перпендикулярна отвесной линии, то условия видимости небесных светил различны для мест на поверхности Земли с различной географической широтой j. Это явление, известное уже в древности, служило одним из доказательств шарообразности Земли. На экваторе (j = 0°) ось мира PP' располагается в плоскости горизонта и совпадает с полуденной линией NS. Суточные параллели (KK', MM') всех светил пересекают плоскость горизонта под прямыми углами. Здесь все светила являются восходящими и заходящими.

По мере перемещения наблюдателя по земной поверхности от экватора к полюсу наклон оси мира к горизонту увеличивается. Всё большее число светил становится незаходящими и невосходящими. На полюсе (j = 90°) ось мира совпадает с отвесной линией, а плоскость экватора — с плоскостью горизонта. Здесь все светила разделяются только на незаходящие и невосходящие, так каких суточные параллели (KK', MM') располагаются в плоскостях, параллельных горизонту

Системы небесных координат используются в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, системы небесных координат являются сферическими системами координат, в которых третья координата — расстояние — часто неизвестна и не играет роли. Эти системы отличаются друг от друга выбором основной плоскости и началом отсчёта.

В зависимости от поставленной задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

Горизонтальная система координат

В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.

Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)

Первая экваториальная система координат

В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.

Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.

Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0^h до 24^h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0^h до +12^h) к западу и от 0° до −180° (от 0^h до −12^h) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α. Прямым восхождением α светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).

Эклиптическая система координат

В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.

Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до -90° к южному полюсу эклиптики.

Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.

Галактическая система координат

В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.

Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило. Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до -90° к южному галактическому полюсу.

Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.

Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).

Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

Изменения координат при вращении небесной сферы

Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.

История и применение

Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.

Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.

ТЕОРИИ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ

Решаемые Теорией движения небесных тел задачи разделяются на две большие группы:

I. Разработка общих вопросов движения небесных тел в гравитационном поле, так называемая задача n тел, частными случаями которой являются задача трёх тел  (в астрономии, задача о движении трёх тел, взаимно притягивающихся по закону тяготения Ньютона и рассматриваемых как материальные точки) и задача двух тел.

Классический пример трёх тел задачи — система Солнце, Земля, Луна. В 1912г. финский астроном К.Ф. Сундман нашёл общее решение этой задачи в виде рядов, сходящихся для любого момента времени t. Однако ряды Сундмана оказались совершенно бесполезными для практических вычислений вследствие их крайне медленной сходимости. При некоторых специальных начальных условиях можно получить очень простые решения задачи трёх тел (решения Лагранжа), представляющие большой интерес для астрономии. Это точки либрации (положения относительного равновесия в задаче небесной механики о движении тела малой массы в силовом поле, не зависящем от времени во вращающейся системе координат), в которых тело малой массы может находиться в состоянии относительного равновесия по отношению к двум др. небесным телам (так называемая, ограниченная задача трёх тел). Для системы двух тел (рассматриваемых как точечные притягивающие массы) существуют три коллинеарные точки либрации, лежащие на прямой, проходящей через эти тела, и две треугольные точки либрации, расположенные таким образом, что два тела и точки либрации образуют равносторонние треугольники.

В коллинеарных точках либрации тела находятся в неустойчивом равновесии. Для астродинамики представляют интерес точки либрации систем Земля — Луна и Солнце — Земля.

Частным случаем трёх тел задачи является так называемая ограниченная задача трёх тел, в которой два тела конечной массы движутся вокруг центра инерции по эллиптическим орбитам, а третье тело имеет бесконечно малую массу. Для ограниченной задачи удалось исследовать разнообразные классы периодических движений. Для общего случая задачи трёх тел подробно изучены предельные свойства движения при t ® +Ґ и t ® —Ґ, то есть так называемые финальные движения.

 В задаче двух тел, притягивающиеся тела принимаются за материальные точки, что справедливо, если они имеют сферическую структуру или если расстояния между ними весьма велики сравнительно с их размерами. Это условие в значительной мере выполняется для Солнца и каждой из планет. При решении задачи двух тел обычно рассматривают движение одного тела относительно другого. Движение в этой задаче происходит по коническим сечениям — окружности, эллипсу, параболе, гиперболе, прямой, — согласно законам Кеплера. Задача двух тел, описывающая т. н. невозмущённое движение, является первым приближением при изучении истинных движений небесных тел.

Так как общее математическое решение задачи n тел имеет очень сложный характер и не может быть использовано в конкретных вопросах, в небесной механике рассматриваются отдельные частные задачи, решение которых основывается на тех или иных особенностях Солнечной системы. Так, в первом приближении, движение планеты или кометы можно рассматривать как происходящее в поле тяготения одного только Солнца. В этом случае уравнения движения допускают решение в конечном виде (задача двух тел). Дифференциальные уравнения движения системы больших планет решаются с помощью разложения в математические рады (аналитические методы) или путём численного интегрирования. Теория движения спутников во многих отношениях аналогична теории движения больших планет, однако, она имеет важную особенность: масса планеты, являющаяся в этом случае центральным телом, значительно меньше массы Солнца, вследствие чего его притяжение существенно возмущает движения спутников.

На движение близких к планете спутников большое влияние оказывает также отклонение её формы от сферической.

Особенностью движения Луны является то обстоятельство, что её орбита расположена целиком вне сферы действия тяготения Земли, т. е. за пределами той области, где притяжение Земли преобладает над притяжением Солнца. Поэтому при построении теории движения Луны приходится осуществлять больше последовательных приближений, чем в планетных задачах. В современной теории движения Луны за первое приближение принимается не задача двух тел, а так называемая задача Хилла - специальный случай задачи трёх тел (обычно под ограниченной задачей трёх тел понимают изучение движения материальной точки P3 под действием притяжения точками P1 и  P2 ; точки  P1 и  P2  движутся по кеплеровским орбитам; точка P3 может иметь и не плоское движение и её действие на точки P1 и  P2 не учитывается; масса материальной точки P3 принимается равной нулю), решение которой даёт промежуточную орбиту, более удобную для проведения процесса последовательных приближений, чем эллипс.

Построение математических теорий движения конкретных небесных тел как естественных, так и искусственных (планет, спутников, комет, космических зондов).

Орбиты небесных тел - траектории, по которым движутся небесные тела в космическом пространстве. Формы орбит небесных тел и скорости, с которыми по ним движутся небесные тела, определяются силой тяготения, а также силой светового давления, электромагнитными силами, сопротивлением среды, в которой происходит движение, приливными силами, реактивными силами (в случае движения ядра кометы) и многое др.

В движении планет, комет и спутников планет, а также в движении Солнца и звёзд в Галактике решающее значение имеет сила всемирного тяготения. На активных участках орбит искусственных космических объектов наряду с силами тяготения определяющее значение имеет реактивная сила двигательной установки. Ориентация орбиты в пространстве, её размеры и форма, а также положение небесного тела на орбите определяются величинами (параметрами), называемыми элементами орбиты.

Элементы орбит планет, комет и спутников определяются по результатам астрономических наблюдений в три этапа:

вычисляются элементы т. н. предварительной орбиты без учёта возмущений, т. е. решается задача двух тел. Для этой цели в большинстве случаев достаточно иметь три наблюдения (т. е. координаты трёх точек на небесной сфере) небесного тела (например, малой планеты), охватывающие промежуток времени в несколько дней или недель.

Осуществляется улучшение предварительной орбиты (т. е. вычисляются более точные значения элементов орбиты) по результатам более длительного ряда наблюдений.

Вычисляется окончательная орбита, которая наилучшим образом согласуется со всеми имеющимися наблюдениями.

Для многих тел Солнечной системы, в том числе для больших планет, Луны и некоторых спутников планет, имеются уже длительные ряды наблюдений. Для вычисления по этим наблюдениям окончательной орбиты (или, как говорят, для разработки теории движения небесного тела) применяются аналитические и численные методы небесной механики.

В результате первого этапа орбита определяется в виде конического сечения (эллипса, иногда также параболы или гиперболы), в фокусе которого находится другое (центральное) тело. Такие орбиты называются невозмущёнными или кеплеровыми, т.к. движение небесного тела по ним происходит по законам Кеплера.

Напомним:

Первый закон Кеплера (Закон эллипсов)

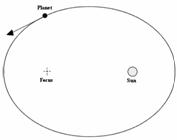
Каждая планета Солнечной системы обращается по эллипсy, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением

,

где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму

Вспомним, что в полярных координатах

В координатной форме запишем

Подставляя и во второе уравнение, получим

которое упрощается

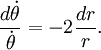
После интегрирования запишем выражение

для некоторой константы , которая является удельным угловым моментом ().Пусть

Уравнение движения в направлении становится равным

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

где G — универсальная гравитационная константа и M — масса звезды.

В результате

Это дифференциальное уравнение имеет общее решение:

для произвольных констант интегрирования e и θ₀.

Заменяя u на 1/r и полагая θ₀ = 0, получим:

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Второй закон Кеплера (Закон площадей)

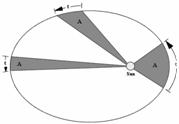
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, заметает сектора равной площади.

Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кепплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии бо́льшую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

По определению угловой момент точечной частицы с массой m и скоростью записывается в виде:

.

где - радиус-вектор частицы а - импульс частицы.

По определению

.

В результате мы имеем

.

Продифференцируем обе части уравнения по времени

поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что - константа.

Третий закон Кеплера (Гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.

,

где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:

,

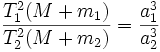где M – масса Солнца, а m₁ и m₂ – массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Шестью элементами, определяющими гелиоцентрическую невозмущённую О. н. т. Р (рис.), являются:

наклон орбиты к плоскости эклиптики i.

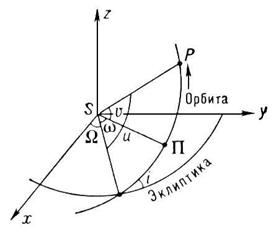
Может иметь любое значение от 0 до 180°; наклон считается меньшим 90°, если для наблюдателя, находящегося в северном полюсе эклиптики, движение планеты имеет прямое направление (против часовой стрелки), и большим 90° при обратном движении. Долгота узла W. Это — гелиоцентрическая долгота точки, в которой планета пересекает эклиптику, переходя из Южного полушария в Северное (восходящий узел орбиты). Долгота узла может принимать значения от 0 до 360°.Большая полуось орбиты а. Иногда вместо а в качестве элемента орбиты принимается среднее суточное движение n (дуга орбиты, проходимая телом за сутки). Эксцентриситет орбиты е. Если b – малая полуось орбиты, то е = /a. Вместо эксцентриситета иногда принимают угол эксцентриситета j, который определяется соотношением sin j = е. Расстояние перигелия от узла (или аргумента перигелия) w. Это гелиоцентрический угол между восходящим узлом орбиты и направлением на перигелий орбиты, измеряемый в плоскости орбиты в направлении движения планеты; может иметь любые значения от 0 до 360°. Вместо элемента w применяется также долгота перигелия p = W + w. Элемент времени, т. е. эпоха (дата), в которую планета находится в определённой точке орбиты. В качестве такого элемента может служить, например, момент t, в который планета проходит перигелий. Положение планеты на орбите определяется аргументом широты и, который представляет собой угловое расстояние планеты вдоль орбиты от восходящего узла, или истинной аномалией v —угловым расстоянием планеты от перигелия. Аргумент широты меняется от 0 до 360° в направлении движения планеты. Аналогичными элементами определяются орбиты комет, Луны, спутников планет, компонентов двойных звёзд, Солнца в Галактике и др. небесных тел.

МЕТОДЫ КОСМИЧЕСКОЙ ГЕОДЕЗИИ

Основным методом космической геодезии является одновременное наблюдение спутника с наземных пунктов. При этом измеряются самые разнообразные параметры относительно положения пунктов и спутников. Параметрами могут служить дальность, скорость изменения дальности (или радиальная скорость), угловая ориентация линии визирования пункт—спутник в какой-либо системе координат, скорость изменения углов и т. д. Измерительные средства располагаются на наземных пунктах. На спутнике же размещается аппаратура, обеспечивающая работу этих измерительных средств. Спутник — это вспомогательный маяк для проведения измерений относительно положения опорных пунктов, причем этот маяк может быть как пассивным, так и активным. В первом случае спутник, освещенный солнцем или имеющий специальную лампу-вспышку, фотографируется с наземных пунктов на фоне звездного неба.

Синхронные наблюдения искусственных спутников Земли, наблюдения искусственных космических объектов, выполняемые одновременно из двух или более точек земной поверхности ведутся методами, позволяющими определять либо направление на спутник (позиционные наблюдения), либо расстояние до него (дальномерные наблюдения), либо обе эти величины одновременно. Результаты таких наблюдений используются для решения астрономических, геофизических и особенно геодезических задач. Направления на ИСЗ, определённые одновременно с двух станций наблюдений, положения которых известны в той или иной системе координат, позволяют вычислить координаты спутника в той же системе и положение плоскости, проходящей через обе станции и спутник (т. н. плоскость синхронизации). Если известны координаты только одной станции, то такие наблюдения позво