Скачать

Оптимизационные модели межотраслевого баланса

Содержание:

Содержание.. 2

Введение.. 3

§ 1. ОБЩАЯ ЛИНЕЙНАЯ ОПТИМИЗАЦИОННАЯ МОДЕЛЬ.. 4

Построение модели. 4

Оптимальные оценки и анализ оптимального плана. 6

Влияние изменения ограничений. 8

Включение в оптимальный план дополнительных производственных способов. 12

§ 2. ОПТИМИЗАЦИОННЫЕ МОДЕЛИ НА ОСНОВЕ МАТРИЦЫ МЕЖОТРАСЛЕВОГО БАЛАНСА.. 14

Модель межотраслевого баланса как частный случай оптимизационных моделей. 14

График оптимизационной модели. 16

Оптимизационная модель межотраслевого баланса продукции и производственных мощностей. 17

§ 3. ОПТИМИЗАЦИОННЫЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ С ПРОИЗВОДСТВЕННЫМИ СПОСОБАМИ.. 24

Теорема 1. При положительном векторе конечной продукции Y⁰ > 0 производятся все продукты и каждый продукт производится только одним способом. 25

Теорема 2. Базис оптимального плана, а следовательно, и выбор «лучших» способов остаются постоянными при любых изменениях положительного вектора Y⁰. 27

Второй вариант модели (максимизация конечной продукции в заданном ассортименте при ограниченных трудовых ресурсах). 29

Варианты модели с различными условиями максимизации конечной продукции. 31

§ 4. РАСШИРЕННЫЕ ОПТИМИЗАЦИОННЫЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ 34

Вывод.. 42

Введение:

В данном реферате рассмотрены проблемы построения и использования оптимизационных моделей межотраслевого баланса.

Анализировавшиеся в данном реферате опти­мизационные межотраслевые модели характеризуются двумя спе­цифическими свойствами. Во-первых, в оптимальный план вклю­чается только по одному способу для каждого производимого вида продукции независимо от того, какое количество способов вводится в условия задачи. Во-вторых, объемы и структура используемой конечной продукции не оказывают никакого влияния на выбор производственных способов и определение общественно необходи­мых затрат на производство продукции.

Хотя выявленные свойства создают значительные удобства при проведении оптимизационных расчетов и анализе оптимальных решений, они не являются адекватным отражением свойств реаль­ной экономики. Данные свойства моделей обусловлены тем, что выбор производственных способов осуществляется с позиций наи­более эффективного использования только одного ограниченного ресурса – труда. Решения, получаемые с помощью рассматривае­мых моделей, должны интерпретироваться как условно-оптималь­ные, т. е. получаемые в предположении, что трудовые ресурсы яв­ляются единственным дефицитным ресурсом в народном хозяйстве. Эти условно-оптимальные решения должны затем корректироваться с учетом использования других ограниченных ресурсов.

§1. ОБЩАЯ ЛИНЕЙНАЯ ОПТИМИЗАЦИОННАЯ МОДЕЛЬ

Линейная оптимизационная модель общего вида впервые была сформулирована и исследована Л. В. Канторовичем. Она получила название основной задачи производственного планирования. Данная модель является частным случаем абстрактной модели оптимального планирования народного хозяйства, в которой целевая функция и все ограничения являются линей­ными.

.ывод:кние:ложнение мо­дели (9.________________________________________________________________________________________________Построение модели.

В народном хозяйстве имеется множество производственных спо­собов ψ Î N; x_ψ- интенсивность применения способа ψ; А = (а_sψ) - вектор производственного способа ψ, компоненты ко­торого означают выпуск продукции и затраты ресурсов при еди­ничной интенсивности его применения. Все множество ингредиен­тов Î М разбивается на два подмножества:

· продукты и воспроизводимые ресурсы (продукты для промежу­точного и конечного использования) ₁Î М₁;

· невоспроизводимые ресурсы ₂ÎМ₂;

Основные ограничения линейной модели производства необходимо конкретизировать лишь в отношении структуры ко­нечной продукции.

В составе конечной продукции выделим постоянную и перемен­ную части: Постоянная часть включает минимально необходимые объемы продукции для непроизводственного потребления (это могут быть объемы, достигнутые в прошедшем периоде), накопления, возмещения выбытия основных фондов» внешнеторгового обмена и т. д. Переменная часть конечной продукции максимизируется в заданном ассортименте в соответствии с условиями:

где - число комплектов переменной части конечной продукции, - количество продукции ₁в одном комплекте.

Общая модель имеет следующий вид:

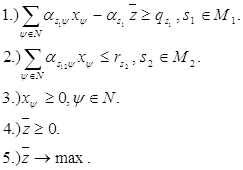(1)

Условия (1) из модели (1) означают балансы производства и распределения продукции, условия (2) - балансы невоспроизво­димых ресурсов.

Для того чтобы задача (1) имела решение, необходимо, чтобы, во-первых, матрица выпуска и материальных затрат производст­венных способов обладала свойством, аналогичным свой­ству продуктивности матрицы (Е — А) межотраслевого баланса (т. е. обеспечивала бы возможность получения положительной ко­нечной продукции) и, во-вторых, чтобы значения не были че­ресчур большими, т. е. такими, чтобы при выполнялись ограничения (2).

Важной качественной характеристикой оптимального плана модели (1) является число применяемых производственных спо­собов (переменных ).

Из теории линейного программирования известно, что оптималь­ный план задачи в случае его единственности и невырожденности содержит столько положительных основных и дополнительных (приводящих неравенства к равенствам) переменных, сколько имеется ограничений. При этом число положительных основных переменных равно числу ограничений, которые в оптимальном плане обращаются в равенства.

Единственность и невырожденность оптимального плана можно рассматривать как типичное свойство модели (1). Очевидно также, можно принять допущение, что в оптимальный план включается переменная . Отсюда следует, что если п – число видов про­дукции и т – число невоспроизводимых ресурсов, то максималь­ное число применяемых производственных способов равно п + т – 1 (из общего числа N). В действительности же число применяемых способов будет равно п₁ + m₁– 1 , где ₁ и m₁– число видов про­дукции и ресурсов, по которым в оптимальном плане неравенства превращаются в равенства (п₁ ≤ , m₁≤m).

Оптимальные оценки и анализ оптимального плана.

Модели (1) соответствуют оптимальные оценки всех видов продукции и невоспроизводимых ресурсов . Их экономи­ческая интерпретация вытекает из анализа общих свойств опти­мальных оценок народнохозяйственной модели.

Оценка 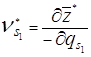характеризует уменьшение максимального числа комплектов конечной продукции при увеличении постоянной части конечной продукции вида₁ на «малую единицу». Оценка 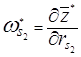показывает прирост максимального числа комплектов при увеличении ресурса s₂ на «малую единицу».

Соотношения, определяющие значения оптимальных оценок, выводятся из условий двойственной задачи.

Все оценки неотрицательны. При этом оценки хотя бы одного вида продукции и хотя бы одного вида ресурсов должны быть по­ложительны (в противном случае план, относительно которого рассчитаны оценки, может быть улучшен).

Для каждого производственного способа выполняются соотношения

(2)

означающие, что суммарная оценка выпускаемой продукции не превышает суммарной оценки всех затрачиваемых ресурсов.

Из условий дополняющей нежесткости следует:

если (3)

если (4)

если (5)

если (6)

если (7)

если (8)

Кроме того, при выполняется равенство

Если ассортиментные коэффициенты пронормированы так, что то значения оценок продукции колеблются вокруг единицы (если оценки некоторых видов продукции меньше единицы, то оценки каких-нибудь других видов продукции больше единицы).

При использовании оптимизационных моделей в планировании никогда не ограничиваются расчетом только одного оптимального варианта. Необходимо анализировать, какие изменения произой­дут в оптимальном плане, если изменяются некоторые исходные данные. Такой анализ особенно важен потому, что исходная ин­формация для народнохозяйственных моделей не может опреде­ляться строго однозначно. Анализ оптимального плана должен показывать пути корректировки и дополнения исходной инфор­мации.

Рассмотрим некоторые, направления анализа оптимального плана.

Влияние изменения ограничений.

Зависимости максимального значения целевой функции (максимума числа комплектов конечной продукции) от изменения параметров ограничений и (каж­дого в отдельности) непосредственно характеризуются значениями оптимальных оценок продукции и ресурсов. Пропорциональное изменение (увеличение или уменьшение) всех параметров ограни­чений не меняет значений оценок. При увеличении оценки ра­стут (до тех пор, пока существует решение задачи). При увеличе­нии оценки снижаются (до нуля).

Возможности эквивалентной взаимозаменяемости конечной про­дукции и ресурсов в ограничениях модели определяются уравне­нием

(9)

Следует заметить, что количественные соотношения эквивалент­ной взаимозаменяемости, вытекающие из уравнения (9), справед­ливы только при таких значениях и , которые не изме­няют значений оптимальных оценок.

Для того чтобы проанализировать влияние изменения ограни­чений на интенсивность применения различных производственных способов, осуществим упорядочение условий задачи.

Будем исходить из того, что для оптимального плана (п₁ + m₁) ограничений выполняются как равенства, а остальные (п – ₁) + (т – m₁) ограничений выполняются как строгие неравенства. Перенумеруем все исходные ограничения так, чтобы первые (п₁ + m₁) ограничений выполнялись как равенства, а остальные – как неравенства.

Выше мы пришли к выводу, что в оптимальном плане положи­тельными будут переменные (п₁ + m₁– 1) производственных спо­собов и переменная . Изменим нумерацию переменных так, чтобы положительные переменные способов заняли первые места (век­тор X₁),aза ними – переменная .

Тогда матрица модели может быть представлена в виде следую­щей блочной матрицы:

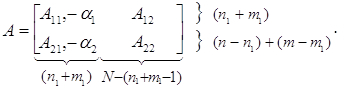
Введем новое обозначение для вектора ограничений: = . Перенумеруем компоненты этого вектора в соответствии с новой нумерацией ограничений: = .

Для оптимального плана справедливо уравнение:

,

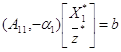откуда

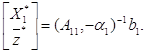(10)

Обозначим первые (п₁ + m₁– 1) строк матрицы через B₁₁, а последнюю строку – через β₁₁. Тогда

(11)

(12)

Формулы (11) и (12) характеризуют зависимости оптималь­ных интенсивностей производственных способов и максимального числа комплектов от «жестких» ограничений задачи. Коэффици­енты матрицы B₁₁ являются аналогами коэффициентов полных потребностей в продукции модели межотраслевого баланса. Од­нако эти коэффициенты могут иметь различные знаки, также как и коэффициенты вектора β₁₁.

Из (11) и (12) выводятся формулы корректировки интенсив­ностей применяемых способов и числа комплектов конечной про­дукции при изменении ограничений:

(13)

(14)

Однако формулы (13) и (14) верны только при сохранении базиса оптимального плана задачи (набора векторов, соответст­вующих положительным переменным). Из линейного программи­рования известно, что базис оптимального плана не изменяется, пока переменные, вошедшие в оптимальный план, будут неотрица­тельны. Это означает, что в анализируемой модели условиями со­хранения базиса оптимального плана являются

(15) или (16)

(17)

Из этих условий находятся границы допустимых изменений каждой компоненты вектора и области допустимых изменений одновременно нескольких компонент вектора . Сохранение ба­зиса оптимального плана является также условием неизменности оптимальных оценок.

Включение в оптимальный план дополнительных производствен­ных способов.

Как уже отмечалось, типичным свойством оптималь­ного плана модели является использование (п₁+ т₁ – 1) произ­водственных способов. Может оказаться, что большая часть имею­щихся производственных способов (из общего числа N > ₁ + т₁ – 1) не будет использоваться и преобладающая часть продукции будет производиться небольшим числом способов. Такая ситуация является нежелательной с точки зрения маневренности, надежности, адаптивности плана. В связи с этим интересно изучить, к каким последствиям приводит включение в оптимальный план дополнительных способов.

Эффективность производственных способов ψ измеряется оценками производственных способов:

. (18)

Для способов, вошедших в оптимальный план, Δ_ψ = 0. Для способов, не вошедших в оптимальный план, Δ_ψ ≤ 0 (а в случае единственности оптимального плана Δ_ψ строго отрицательны). Оценки Δ_ψ показывают, насколько уменьшится значение целевой функции при включении в оптимальный план ранее не входившего в него способа с единичной интенсивностью. Если же интенсивность вводимого способа равна x_ψ, то значение целевой функции умень­шится на Δ_ψx_ψ.

Рассмотрим, как повлияет включение дополнительных способов (вектора Х₂) на интенсивности применения оптимальных (базис­ных) способов (вектор X₁. Добавив к вектору ₁произведение – A₁₂ Х₂, получим на основе (11)

,

откуда

(19)

Заметим также, что формула изменения максимального числа комплектов конечной продукции при включении вектора Х₂ имеет вид:

(20)

Формулы (19) и (20) справедливы при сохранении базиса оптимального плана, т. е. при условиях

С помощью оценок способов (18) можно изучать целесообраз­ность включения в условия народнохозяйственной задачи новых способов. Новый способ φ будет эффективным (т. е. может войти в оптимальный план), если Δ_φ ≥ 0. Это условие может быть использовано для проектирования новых эффективных производст­венных способов.

Рассмотренные направления и методы анализа оптимального плана являются универсальными для всех линейных оптимиза­ционных моделей. Однако в более частных моделях экономико-математический анализ может выявлять и специфические свойства оптимальных решений.

§2. ОПТИМИЗАЦИОННЫЕ МОДЕЛИ НА ОСНОВЕ МАТРИЦЫ МЕЖОТРАСЛЕВОГО БАЛАНСА

Общая линейная оптимизационная модель построена на основе матрицы таких производственных способов, что каждый из них мо­жет выпускать несколько видов продукции, каждый вид продукции может выпускаться несколькими способами.

Далее мы рассмотрим более частные оптимизационные модели, сохраняющие некоторые специфические допущения модели межотраслевого баланса: сначала – модели, в которых каждый способ выпускает только один продукт и каждый продукт выпускается только одним способом, а затем – модели, в ко­торых сохраняется только первое из указанных допущений. Такая последовательность анализа моделей выбрана для того, чтобы «перекинуть мост» между моделями межотраслевого баланса и оптимизационными моделями народного хозяйства и проследить изменение свойств решений (сбалансированных и оптимальных) при изменении предпосылок модели и включении в нее новых ус­ловий.

Модель межотраслевого баланса как частный случай оптимизационных моделей

Оптимизационные модели по сравнению с балансовыми пред­ставляют собой более совершенный тип моделей социалистической экономики. Однако было бы неправильно противопоставлять их друг другу. Во-первых, основные условия балансовых моделей обязательно включаются в оптимизационные модели. Во-вторых, балансовые модели могут интерпретироваться и исследоваться как частный случай оптимизационных моделей.

Попытаемся сформулировать модель межотраслевого баланса на языке оптимизационных задач. Рассмотрим систему уравнений межотраслевого баланса производства и распределения продукции совместно с ограничением по трудовым ресурсам производствен­ной сферы:

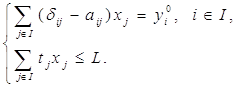(21)

Основная задача плановых расчетов с помощью этой модели состоит в том, чтобы при заданном векторе Y⁰ = () и имеющихся трудовых ресурсах L найти вектор необходимых объемов произ­водства X = (x_j). Покажем, что эту задачу можно представить в виде задачи линейного программирования:

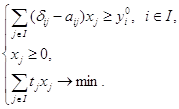(22)

Эта задача отличается от (21) только тем, что допускается полу­чение конечной продукции сверх заданных минимальных объемов, а затраты трудовых ресурсов минимизируются. Очевидно, что ре­альным экономическим условиям отвечают только такие решения X* = (x*), при которых .

Задаче (22) соответствует двойственная задача, с помощью которой находятся оптимальные оценки продукции :

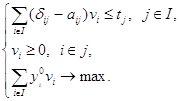(23)

Оптимальный план X* задачи (22) характеризуется следую­щими свойствами:

· он единственный;

· если Y⁰ > 0 (или Y⁰≥ 0 и А – неразложимая матрица), то Х* > 0;

· балансы производства и распределения продукции выполняются строго как равенства, т. е. излишки конечной продукции не про­изводятся;

· оптимальный план X* не зависит от коэффициентов целевой функции t_J≥ 0.

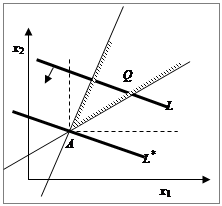На рис. 1 видно, что оптимальный план всегда является вер­шиной «клюва» при любых допустимых наклонах целевой функции. Обе задачи (и прямая, и двойственная) всегда имеют единственное решение, если матрица А продуктивна иY⁰ ≥ 0. При этом реше­ние прямой оптимизационной задачи сводится к решению системы уравнений и поэтому оно не зависит от значений коэффициентов минимизируемой функции. Решение двойственной задачи находится из системы урав­нений ипоэтому оно не зависит от коэффициентов минимизируемой функции. При этом оптимальные оценки продук­ции равны коэффициентам полных трудовых затрат.

Равенство функционалов прямой и двойственной задачи имеет место при любых положительных значениях t_jи . Оно означает, что суммарная оценка всей конечной продукции равна сумме трудовых затрат в народном хозяйстве.

Оптимизационная модель межотраслевого баланса продукции и производственных мощностей.

При анализе возможностей использования модели межотрасле­вого баланса в планировании отмечалось, что при крат­косрочном планировании наиболее существенными ограничениями роста производства являются наличные производственные мощности.

Решение модели должно удовлетворять условиям x_j ≤ N_j, где N_j– максимально возможный выход продукции j с производст­венных мощностей планируемого года. Так же, как и в § 1, вклю­чим в модель условия оптимизации конечной продукции (27), обозначая вектор ассортиментных коэффициентов прироста конеч­ной продукции, а вектор заданных объемов конечной про­дукции Q = (q_i).

В векторно-матричных обозначениях модель имеет вид:,

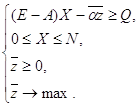(24)

Решение модели существует, если значения компонент вектора Qзаданы не слишком большими. Оптимальный план обращает пер­вую группу условий строго в равенства (невыгодно производить сверхкомплектные излишки конечной продукции). Поэтому в даль­нейшем анализе исходим из того, что (Е – А) X–= Q, откуда

(25)

Поскольку , то при условие Х ≥ 0 всегда выполняется. Вследствие этого задача сокращается:

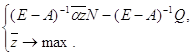
Вектор представляет собой коэффициенты пол­ных потребностей в продукции для получения одного комплекта конечной продукции; есть вектор макси­мально возможных объемов продукции для получения перемен­ной части конечной продукции. Очевидно, что

(26)

Определив , находим X* = β+ (E– A)^–1Q.

Таким образом, определяется «узким» местом в системе про­изводственных мощностей. Как правило, мощность только одного вида продукции будет использована полностью. Оптимальная оценка мощности по этому виду продукции (k) равна .

Выявление дефицитной мощности служит сигналом для ее максимального расширения в планируемом году за счет концентрации строительства на пусковых объектах, дополнительных поставок оборудования, изменения специализации соответствующих пред­приятий и режима их работы (сменности) и т. д.

Для определения программы первоочередных мероприятий по расширению производственных мощностей целесообразно упорядочить мощности по их дефицитности.

Для каждого вида мощности рассчитаем показатель , характеризующий максимальное число комплектов конечной про­дукции, которое можно получить с мощности вида j при условии неограниченности других мощностей. Упорядочив ряд чисел , начиная с , получим последовательность мощностей, упорядоченную по степени их дефицитности. При новой нумерации разности покажут прирост числа комплектов ко­нечной продукции после «расшивки» k-го«узкого» места в системе производственных мощностей.

По модели (24) можно проводить многовариантные расчеты, показывающие влияние изменения параметров а_ij,, N_jна объемы производства и конечной продукции. В результате таких расчетов выявляется группа устойчиво дефицитных мощностей, на расши­рение которых ресурсы должны направляться в первую очередь. Важным направлением развития модели является непосредственный учет в ней элементов случайности и неопределенности. Разработана и экспериментально апробирована модель, в которой про­изводственные мощности N_i рассматриваются как случайные не­зависимые величины.

Модели с ограничениями по общим ресурсам.

Рассмотрим модель, в которой балансы производства и распре­деления продукции дополняются ограничениями по общим невос­производимым ресурсам:

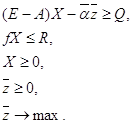(27)

Подставляя (25) в ограничения по общим ресурсам, получаем

или

(28)

где = (_s) = (E – А)^–1 – вектор полных затрат ресурсов на один комплект прироста конечной продукции, – вектор ресурсов, которые могут использоваться для получения переменной части конечной продукции.

Из (28) следует:

(29)

Максимальное число комплектов достигается, как правило, при полном использовании только одного ресурса (k). Тогда только оценка этого ресурса будет положительна: , a оптимальные оценки всех видов продукции будут пропорциональны коэффициентам полных затрат дефицитного ресурса: .Если же в оптимальном плане используются полностью несколько ресур­сов, то система оптимальных оценок ресурсов и продуктов будет неединственной.

Полное использование только одного вида ресурсов (или нали­чие только одного «узкого» места) как типичное свойство оптималь­ного решения не обязательно связано с условиями максимизации конечной продукции в заданном ассортименте. Для сравнения рассмотрим модель, в которой условия максимизации переменной ча­сти конечной продукции заданы в виде ЦФП:

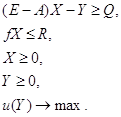(30)

Выражая Xчерез Y, приходим к сокращенной модели:

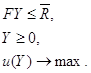(31)

где F = f (Е – А) ^–1 – матрица коэффициентов полных затрат ресурсов, .

Оптимальное решение этой модели всегда существует и является единственным. Оптимальный план Y* есть точка касания наибо­лее удаленной от начала координат поверхности безразличия и вы­пуклого многогранника, образованного условиями . Если эта поверхность безразличия касается вершины многогранника, то это означает полное использование нескольких ресурсов. Очевидно, что в случае применения ЦФП вероятность того, что точкой опти­мума будет вершина многогранника, выше, чем в случае приме­нения ассортиментного критерия. Однако вполне возможно, что максимум u(Y)достигается на одной из граней многогранника, т. е. при полном использовании только одного ресурса.

Таким образом, общим свойством рассмотренных в этом пара­графе моделей является то, что оптимальный план чаще всего достигается при полном использовании только одного ресурса. А это означает, что только один вид ресурсов влияет на формирование оптимального решения. Данное свойство не адекватно экономиче­ской реальности; оно обусловлено недостатком моделей.

В моделях (24), (27), (30) почти отсутствуют возможности маневрирования ресурсами, имеющими различную дефицитность. По каждому виду продукции задается только один производствен­ный способ, а поэтому технология производства не реагирует на выявляющиеся в процессе оптимизации соотношения наличия ре­сурсов и потребностей в них. Благодаря корректировке исходных данных на основе анализа оптимальных решений этот недостаток можно преодолевать лишь отчасти.

Напрашивается вывод о том, что оптимизационные модели на­родного хозяйства должны включать условия выбора между раз­личными способами- производства одноименной продукции.

§3. ОПТИМИЗАЦИОННЫЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ С ПРОИЗВОДСТВЕННЫМИ СПОСОБАМИ

Первый вариант модели (минимизация затрат труда на производство заданной конечной продукции).

Построим модель, представляющую собой непосредственное обобщение модели межотраслевого баланса, записанной в форме (22). В модели предусматривается возможность выбора между различными производственными способами. Пусть каждый вид продукции производится несколькими способами , где T_j= {1, ... , s_j}.При этом каждым способом выпускается только один продукт. Введем новые обозначения:

– объем производства продукции j способом _j;

– коэффициент пря­мых затрат продукции iна производство единицы продукции j способом _j;

– затраты труда на единицу продукции j, произ­водимой способом _j.

Модель имеет вид:

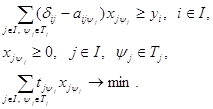(32)

Модель (32) всегда имеет решение, если выполняются усло­вия, аналогичные условию продуктивности матрицы коэффициен­тов прямых материальных затрат модели межотраслевого баланса. Например, одно допустимое решение может быть получено, если включить в план по одному способу для каждого вида продукции, а все остальные переменные считать равными нулю. Так может быть составлено систем уравнений межотраслевого баланса производства и распределения продукции, каждая из которых имеет решение, если матрица продуктивна.

Анализ модели позволяет выявить ряд ее интересных специфи­ческих свойств.

Теорема 1. При положительном векторе конечной про­дукции Y⁰ > 0 производятся все продукты и каждый продукт про­изводится только одним способом.

Доказательство. Напомним, что мы исходим из пред­положения, что оптимальный план – единственный. Введем в ус­ловия дополнительные переменные Δy_i (излишки конечной про­дукции сверх минимально необходимых объемов ), превращающие неравенства в равенства.

В каждом i-м уравнении

положительными являются только коэффициенты при переменных Х. Но поскольку все , то и все , т. е. оптимальном плане должны производиться все виды продуктов.

Максимальное число положительных переменных в оптимальном плане равно п (числу уравнений). Следовательно, в каждой сумме переменных положительной может быть только одна переменная. Иначе говоря, в оптимальном плане каждый продукт про­изводится только одним способом.

Следствие. Из теоремы следует, что поскольку число воз­можных положительных переменных исчерпывается переменными способов производства, то все Δy_iв оптимальном плане равны нулю. Иными словами, оптимальный план обращает исходные неравен­ства строго в равенства.

Введем дополнительные обозначения: X* – оптимальный план модели (каждая его компонента есть интенсивность применения какого-то «лучшего» способа производства); A* – матрица коэффи­циентов материальных затрат, составленная из способов, которые вошли в оптимальный план.

Матрица А* аналогична матрице А межотраслевого баланса с той лишь разницей, что вместо средневзвешенных коэффициентов из разных способов в ней представлены коэффициенты только «луч­ших» способов. Матрицы A* и (Е – А*)обладают теми же экономико-математическими свойствами, что и матрицы межотраслевого ба­ланса. Среди этих свойств отметим, в частности, существование матрицы (Е – А*)^–1 ≥ 0. Элементы матрицы (Е – А*)^–1являются коэффициентами полных потребностей в выпуске продукции для получения единицы конечной продукции в оптимальном плане. Оптимальный план удовлетворяет следующей системе уравнений:

(E – A) X* = Y⁰или X* = (E – A)^–1Y⁰.

Теорема 2.Базис оптимального плана, а следовательно, и выбор «лучших» способов остаются постоянными при любых из­менениях положительного вектора Y⁰.

Доказательство. Для того чтобы базис оптимального плана оставался неизменным при переменном векторе Y⁰, доста­точно – в соответствии с (15),– чтобы выполнялось условие

(E – A*)^–1Y⁰ ≥ 0.

Поскольку матрица (E – A*)^–1 ≥ 0, условие (E – A*)^–1Y⁰ ≥ 0 выполняется всегда при любом Y⁰ ≥ 0 и тем более при Y⁰ > 0.

Пусть для некоторого Y⁰ > 0 получено решение X*. Базис по­лученного решения (Е – А*) остается неизменным и тогда, когда вектор Y⁰ будет изменяться любым образом в положительной об­ласти (0 <Y⁰ < +∞). Если базис оптимального плана – не­разложимая матрица, то теорема распространяется на случай Y⁰ ≥ 0.

Это означает, что вычислив матрицу (E – A*)^–1для одного ва­рианта конечной продукции, можно неоднократно использовать ее для расчета производственной программы при других вариантах конечной продукции.

Из задачи, двойственной к (32), следует, что для способов, вошедших в оптимальный план , выполняются условия

Поэтому вектор оптимальных оценок продукции V* = (), характеризующих минимально необходимый прирост трудовых затрат в народном хозяйстве при увеличении конечной продукции, определяется решением системы уравнений

V* = V* A* + t* или V* = t* (A – V*)^–1.

Видим, что оптимальные оценки продукции в рассматриваемой модели равны коэффициентам полных трудовых затрат, исчислен­ным по лучшим производственным способам для каждого вида про­дукции.

Следствие. Оптимальные оценки не изменяются при любых изменениях положительного вектора Y⁰.

При неизменных коэффициентах производственных способов оптимальные оценки меняются только при изменении базиса оп­тимального плана. Теорема 2 доказывает, что в модели (32) базис оптимального плана остается постоянным при любых изменениях вектора Y⁰ в положительной области, следовательно, не изме­няются и оптимальные оценки(1).

Постоянство оценок облегчает их использование в различных планово-экономических расчетах, в частности, при корректировке вектора Y⁰.

Второй вариант модели (максимизация конечной продукции в заданном ассортименте при ограниченных трудовых ресурсах).

Рассмотрим другую возможную постановку межотраслевой мо­дели с производственными способами: произвести максимальное число комплектов конечной продукции при ограниченных трудо­вых ресурсах:

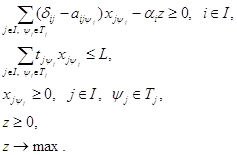(33)

Нетрудно установить, что модели (32) и (33) являются взаимным. В первой модели фиксируются и минимизируются затраты труда, а во второй модели максимизи­руются zпри фиксированном ресурсе труда.

Отсюда