Скачать

Определение географической широты по астрономическим на-блюдениям

Реферат выполнила Белая Екатерина

11-Г класс

Определение географической широты в древние времена. В древние времена, и особенно в эпоху Великих географических открытий, определение координат места было необходимой и первоочередной задачей. На каждом корабле был астроном, который с помощью простейших инструментов был способен определить широту и долготу местонахождения судна.

Долгое время для определение координат использовали якобсштаб – инструмент, представляющий собой длинную градуированную планку, снабженную более короткой подвижной поперечной перекладиной. При визированиии нужно было приставить конец планки к глазу, а поперечную перекладину двигать до тех пор, пока ее нижний конец не коснется горизонта, а верхний – данной звезды или Солнца. Таким образом определялась высота светила, а с ее помощью – широта места и время. Якобсштаб использовался до середины XVIIIв., пока не был вытеснен зеркальным секстантом – астрономический угломерный инструмент, состоящий из зрительной трубы, двух зеркал, светофильтров и шкалы. Секстант был настолько важен для мореплавателей, что его даже поместили на небо, назвав этим словом созвездие.

Система географических координат на поверхности Земли. Земной шар делится плоскостью экватора на два равных полушария –Северное и Южное. Плоскость экватора перпендикулярна к оси вращения Земли. Ось вращения пересекается с земной поверхностью в Северном и Южном полюсах Земли.

Если мысленно пересечь земной шар плоскостями, параллельными экватору, получаются окружности – параллели. Земной шар можно мысленно пересечь перпендикулярными к экватору и проходящими через земную ось плоскостями, которые носят название плоскостей меридианов, а линии, образованные их пересечением с поверхностью земного шара называются меридианами. Любая точка на поверхности земного шара может быть задана двумя координатами. Одна координата называется долготой и отсчитывается от нулевого, условно принятого меридиана, проходящего через Гринвичскую обсерваторию. Вторая координата называется широтой и отсчитывается от земного экватора к полюсам.

Высота полюса мира над горизонтом. Высота полюса мира над горизонтом h_p=Ð PCN, а географическая широта места j=Ð COR. Эти два угла (Ð PCN и Ð COR) равны как углы со взаимно перпендикулярными сторонами: (ОС)^ (CN),(OR)^(CP). Равенство этих углов дает простейший способ определения географической широты местности j: угловое расстояние полюса мира от горизонта равно географической широте местности. Чтобы определить географическую широту местности, достаточно измерить высоту полюса мира над горизонтом, так как:

h_p=j.

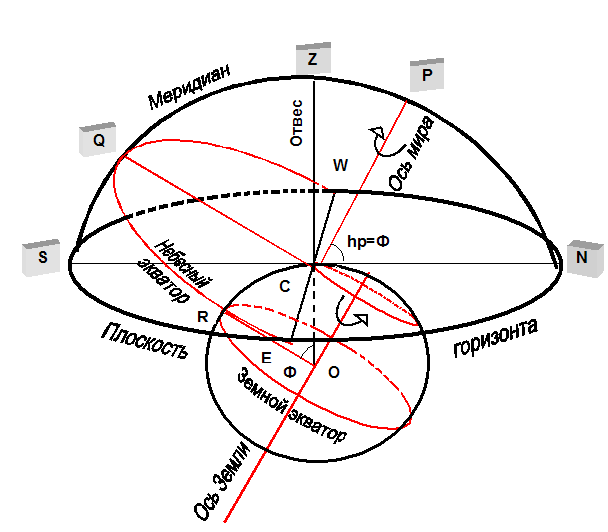
Суточное движение светил на различных широтах. С изменением географической широты места наблюдения меняется ориентация оси вращения небесной сферы относительно горизонта. Необходимо рассмотреть, какими будут видимые движения небесных светил в районе Северного полюса, на экваторе и на средних широтах Земли.

На полюсе Земли полюс мира находится в зените, и звезды движутся по кругам, параллельным горизонту. Здесь звезды не заходят и не восходят, их высота над горизонтом неизменная.

На средних географических широтах существуют как восходящие и заходящие звезды, так и те, которые никогда не опускаются под горизонт. Например, околополярные созвездия на географических широтах СССР никогда не заходят. Созвездия, расположенные дальше от северного полюса мира, показываются ненадолго над горизонтом. А созвездия, лежащие около южного полюса мира, являются невосходящими.

Но чем дальше продвигаешься к югу, тем больше можно увидеть южных созвездий. На земном экваторе, если бы днем не мешало Солнце, за сутки можно было бы увидеть созвездия всего земного неба.

Для наблюдателя на экваторе все звезды восходят и заходят перпендикулярно плоскости горизонта. Каждая звезда здесь проходит над горизонтом ровно половину своего пути. Северный полюс мира для него совпадает с точкой севера, а южный полюс мира – с точкой юга. Ось мира расположена в плоскости горизонта.

Высота светил в кульминации. Полюс мира при кажущемся вращении неба, отражающем вращение земли вокруг оси, занимает неизменное положение над горизонтом на данной широте. Звезды за сутки описывают над горизонтом вокруг оси мира круги, параллельные небесному экватору. При этом каждое светило за сутки дважды пересекает небесный меридиан.

Явления прохождения светил через небесный меридиан называются кульминациями. В верхней кульминации высота светила максимальна, в нижней кульминации - минимальна. Промежуток времени между кульминациями равен половине суток.

У не заходящего на данной широте j светила М видны обе кульминации, у звезд, которые восходят и заходят, нижняя кульминация происходит под горизонтом, ниже точки севера. У светила М₄, находящегося далеко к югу от небесного экватора, обе кульминации могут быть невидимы.

Момент верхней кульминации центра Солнца называется истинным полднем, а момент нижней кульминации – истинной полночью.

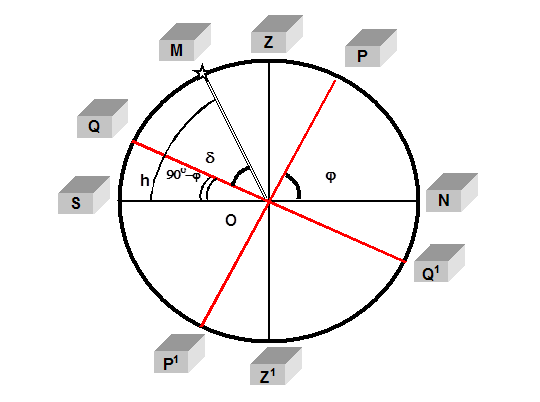
Найдем зависимость между высотой h светила М в верхней кульминации, его склонением d и широтой местности j. ZZ^/ - отвесная линия, РР^/ - ось мира, QQ^/ - проекция небесного экватора, NS – линия горизонта на плоскость небесного меридиана (PZSP^/N).

Высота полюса мира над горизонтом равна географической широте места, т. е. h_p= j. Следовательно, угол между полуденной линией NS и осью мира РР^/ равен широте местности j, т.е. ÐPON=h_p= j. Очевидно, что наклон плоскости небесного экватора к горизонту, измеряемый Ð QOS, будет равен 90⁰- j, так как Ð QOZ=Ð PON как углы с взаимно перпендикулярными сторонами. Тогда звезда М со склонением d, кульминирующая к югу от зенита, имеет в верхней кульминации высоту

h=90^о - j + d.

Из этой формулы видно, что географическую широту можно определить, измеряя высоту любого светила с известным склонением d в верхней кульминации. При этом следует учитывать, что если светило в момент кульминации находится к югу от экватора, то его склонение отрицательно.