Скачать

Некоторые аспекты моделирования конкурентного равновесия

АДЫГЕЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ МАТЕМАТИКИ И КОМПЬЮТЕРНЫХ НАУК

Кафедра информатики и вычислительной техники

КУРСОВАЯ РАБОТА

"НЕКОТОРЫЕ АСПЕКТЫ МОДЕЛИРОВАНИЯ КОНКУРЕНТНОГО РАВНОВЕСИЯ"

Майкоп, 2008

Оглавление

Введение. 3

1. Экономическое равновесие. Содержательный аспект. 4

2. Описание общей модели Вальраса. 9

3. Модель Эрроу-Дебре. Существование конкурентного равновесия. 20

4. Модель регулирования цен и устойчивость конкурентного равновесия. 32

Рассмотренные задачи. 39

Заключение. 41

Список литературы.. 42

Введение

Существует различные системы моделирующие рынок, некоторые описывают его в статическом, некоторые в динамическом состоянии, но большинство из таких систем рассматривают рынок одного продавца и не рассматривают конкурентные рынки. А для того чтобы более подробно изучить поведение рынка при колебании спроса и предложения на ту или иную продукцию необходимо рассматривать системы, моделирующие рынок именно в условиях конкуренции.

В данной работе были рассмотрены некоторые аспекты экономического равновесия, а так же системы, моделирующие рынок в условиях конкурентной среды.

Взаимодействие между складывающимися на рынке готовой продукции потребительским спросом и предложением фирм приводит к понятию равновесия. О равновесии можно говорить, как о характеристике состояния любой системы, на которую воздействуют различные стороны (в частности, только одна сторона), каждая со своими интересами. В таком общем смысле равновесие – это то состояние системы, которое устраивает всех заинтересованных в ее состоянии сторон, за неимением ничего лучшего.

Приведу несколько конкретных понятий.

1. Равновесие в задачах принятия решения со многими участниками. Предположим, что интересы участников (лиц, принимающих решения) не противоположны, но и не совпадают. Однако степень достижения своей цели каждым из них зависит как от его собственных решений, так и от действий всех остальных участников. Под равновесным состоянием данной системы понимается такая ситуация (совокупность выбранных решений), когда отклонение от этой ситуации разве что ухудшает положение уклониста (при условии, что остальные участники придерживаются этой ситуации). Равновесная ситуация не обеспечивает участникам «наилучшее достижение цели», но, если такая ситуация существует, то, в условиях отсутствия обмена информациями участникам ничего другого не остается, как придерживаться ее (дабы хуже не было). Это так называемое равновесие по Нэшу. Оно широко применяется в теории игр – разделе исследования операций, посвященном математическим моделям задач принятия решения в условиях конфликта и неопределенности.

2. Равновесные действия противоборствующих сторон. Такая ситуация предполагает наличие двух лиц, принимающих решения, с прямо противоположными интересами (например, две конкурирующие фирмы, выпускающие один и тот же товар, имеющие один и тот же рынок сбыта). Здесь каждая сторона принимает решение с учетом «закона подлости», т.е. выбирает лучшее из тех решений, которые «разрешены» ее противником. Равновесным является то состояние, одностороннее отклонение от которого невыгодно уклонисту. Такое равновесие называется седловой точкой и, если оно существует, то противники вынуждены ее придерживаться. Видно, что седловая точка является частным случаем равновесия по Нэшу.

3. Равновесие на основе угроз. Этот принцип применяется в задачах принятия решения с обменом информацией. Равновесным называется такое состояние системы, когда любое мотивированное предложение (угроза) одних участников, направленное на изменение данного состояния системы, встречает мотивированное возражение (контругрозу) со стороны других участников.

4. Равновесие в задаче потребителя наилучшее состояние потребителя описывается точками, в которых бюджетные линии касаются соответствующих кривых безразличия. Эти точки характеризуют спрос, во-первых, как платежеспособную потребность в товарах, во-вторых, как набор товаров, максимизирующий полезность потребителя. Отклоняясь от них в своем выборе, потребитель нарушил бы одно из условий «оптимальности». Поэтому данные точки и отражают равновесное состояние потребителя. Аналитически это состояние характеризуется равенством между отношением цен товаров и предельной нормой замещения.

5. Равновесие в задаче фирмы. Условия равновесия в задаче фирмы концептуально схожи с соотношениями, формируемыми в теории спроса. Цель фирмы – максимизация прибыли (или минимизация издержек) при ограниченных ресурсах (при фиксированном уровне выпуска). Набор затрат ресурсов, удовлетворяющих этим условиям, и отражает равновесное состояние производства. Реализация других объемов затрат может привести лишь к нарушению условий «оптимальности». Аналитически состояние равновесия фирмы выражается равенством между отношением цен на соответствующие факторы производства и готовый продукт и предельной нормой замещения.

Характерным свойством «равновесий» в приведенных примерах является их устойчивость против отклонения.

Чтобы понять присуще ли это свойство экономическому равновесию, рассмотрим рынок одного товара, относительно которого будем говорить о совокупном спросе потребительского сектора и о совокупном предложении производственного сектора.

Пусть цена товара фиксирована. Это положение соответствует условиям совершенной конкуренции, когда отдельные участники экономики не влияют на цену товара. Пусть имеет место равновесие: , где - совокупный спрос, - совокупное предложение, – цена товара, – доход потребительского сектора, - цены затрат. Формально это равновесие может быть нарушено либо по «воле» рынка, который распоряжается ценой товара, либо по воле покупателя (управляющего спросом, например, посредством изменения величины дохода) или производителя (управляющего предложением, например, посредством изменения объемов затрат). В первом случае будем говорить о ценовых причинах нарушения равновесия, во втором – о неценовых причинах.

Рассмотрим сначала неценовые причины (вызванные влиянием сезонности, моды, изменением экономической политики и т.д.). Предположим, что при неизменном предложении потребитель «сознательно» отклоняется от равновесия, увеличивая или уменьшая спрос:

a) , b) .

Если при фиксированном спросе от равновесия отклоняется производитель, то соответственно придем к одному из двух неравенств:

c) , d) .

В этих соотношениях случаи a) и c) приводят к дефициту, т.е., в конечном счете, к повышению цены, что выгодно производителю и невыгодно потребителю. Следовательно, в случаях a) и c) неценовые причины вызывают изменение равновесной цены. Случаи b) и d) приводят к излишкам, т.е., в конечном счете, к снижению цены, что выгодно потребителю и невыгодно производителю. Следовательно, в случаях b) и d) неценовые причины также вызывают изменение равновесной цены.

Исходя из таких рассуждений, можно было бы заключить, что потребителю выгодно отклонение от равновесия в сторону снижения спроса, а производителю – в сторону снижения предложения.

Как видно, по отношению к экономическому равновесию однозначно нельзя утверждать о его устойчивости против отклонения. Но зато эти рассуждения помогают обнаружить устойчивость другого характера – тенденцию экономического равновесия к устойчивости против колебания цены, какой бы причиной оно ни было вызвано. Поясним это положение.

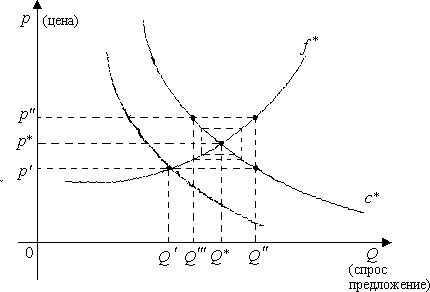
Рис. 1. Устойчивость равновесия против колебания цен.

Будем исходить из того факта, что экономическое равновесие может быть нарушено как по ценовым, так и по неценовым причинам. Пусть на уровне цен имеет место равновесие (точки здесь заменяют прочие, в частности, неценовые, переменные). Допустим, что по какой-то неценовой причине повысился спрос до уровня . Как видно из рис. 1, спрос соответствует цене , так что

т.е. спрос стал больше предложения. Цене соответствуют две точки: и . Естественно поставить вопрос: может ли цена быть равновесной, иначе, может ли одна из этих двух точек быть равновесным состоянием? Обратимся к точке (относительно точки рассуждения зеркально аналогичны).

Для того чтобы точка оказалась равновесной, кривая спроса должна сместиться и пройти через эту точку. Формально это возможно, тогда, когда выполняется равенство . Содержательно, бюджет потребителя должен уменьшиться ровно на величину , и тогда бюджетная линия в пространстве товаров параллельно сместится от точки до точки . Такое изменение ситуации приведет к уменьшению дохода производителя , и оно вызвано двумя причинами: снижением цены и выпуска . При данных неизменных технологических условиях производителю нечего этому противопоставить, так как нежелание снизить цену своего товара или объема выпуска приведет к еще худшему результату. Таким образом, неценовые причины могут привести к переходу в новое состояние равновесия, и это свидетельствует о неустойчивости равновесия против неценовых возмущений в экономике.

Теперь разберём ценовую причину. Пусть цена товара упала до величины . Как видно из рис. 1, при этой цене спрос превышает предложение , что влечет повышение цены товара. Если предложение подтягивается до нового уровня спроса, т.е. до величины , то, согласно кривой предложения, цена должна повышаться до величины . Но такой цене соответствует спрос . Продолжая эти рассуждения, можно заметить, что цена последовательно приближается к равновесному значению , а спрос и предложение сходятся к общему (равновесному) значению . Здесь описана идея процедуры рыночного регулирования цены «невидимой рукой Адама Смита». По расположению вспомогательных линий на графике эту процедуру называют паутинообразной моделью регулирования цены товара. Аналогичную картину можно получить при исходном предположении о повышении цены над .

В результате можно сделать вывод о том, что экономическое равновесие устойчиво против ценовых возмущений.

2. Описание общей модели Вальраса

Исходными концепциями модели Вальраса являются:

· дезагрегированность участников рынка: рассматриваются отдельные потребители и отдельные производители;

· совершенность конкуренции;

· общность равновесия.

Последняя концепция означает рассмотрение равновесия по всем товарам сразу, а не по отдельным товарам. Следовательно, в модели Вальраса вводится понятие общего равновесия (т.е. равновесия по всем товарам).

Будем предполагать, что на рынке продаются и покупаются товары двух видов: готовые товары, являющиеся продуктом производства (товары конечного потребления) и производственные ресурсы (первичные факторы производства). Поэтому будем рассматривать «расширенное» пространство товаров , где n – число видов всех товаров. Компонентами вектора являются как выпуски, так и затраты (первичные факторы). Для различения их, затраты снабжают отрицательным знаком. Если есть вектор чистого выпуска, то все его компоненты, соответствующие затратам, будут равны нулю; если есть вектор только первичных факторов, то все его компоненты, соответствующие конечным продуктам, будут равны нулю.

Индексы (виды) товаров, как и раньше, будем обозначать буквой , индексы потребителей – буквой и индексы производителей – буквой .

Через будем обозначать вектор цен товаров.

Выходя на рынок, каждый потребитель или производитель становится одновременно покупателем одних и продавцом других товаров. Потребитель, т.е. участник рынка, «непосредственно не занятый в производстве», может продавать имеющиеся в его распоряжении первичные факторы и покупает товары производителей. Производитель, т.е. участник рынка, «непосредственно занятый в производстве», продает свою готовую продукцию и покупает первичные факторы у потребителей.

Поэтому каждый потребитель i как участник рынка характеризуется тремя параметрами: начальным запасом товаров , функцией дохода и вектор-функцией спроса на продукты производства .

Каждый производитель j характеризуется двумя параметрами: вектор-функцией предложения готовой продукции и вектор-функцией спроса на затраты . Однако в модели Вальраса применяется несколько обобщенная характеристика производителя – с помощью одного множества , трактуемого как множество его (оптимальных) производственных планов. На языке «затраты-выпуск» это множество можно определить следующим образом: , где – производственная функция. Очевидно, .

С учетом всего вышесказанного, под математической моделью рынка будем понимать совокупность элементов:

(2.1)

где – пространство цен товаров, N – множество всех участников рынка (N содержит l+m элементов).

Без качественных потерь вместо (2.1), как модель рынка, можно рассматривать совокупность

Вектор содержит цены, как товаров конечного потребления, так и затрат. Причем цены меняются не по желанию отдельных участников рынка, а исключительно под воздействием совокупного спроса и совокупного предложения. Поэтому одним из ключевых является вопрос: существуют ли такие цены, которые устраивают как потребителей, так и производителей?

Исходя из технических соображений, будем предполагать, что пространство цен P включает в себя нуль пространства , т.е. будем допускать существование нулевых цен.

Каждый участник рынка выступает в двух лицах: как покупатель и как продавец. Очевидно, число продавцов и покупателей для разных товаров будет разным. Поэтому числа и не следует ассоциировать с числом продавцов и покупателей.

Доход каждого потребителя предполагается состоящим из двух компонент: 1) выручки от продажи принадлежащего ему начального запаса товаров (), 2) дохода, получаемого от его участия в прибыли производственного сектора (обозначим ), например, посредством приобретения ценных бумаг и других видов инвестиционной и трудовой деятельности. Таким образом, предполагаем, что

(2.2)

В модели Вальраса считается, что весь доход производственного сектора полностью распределяется между потребителями:

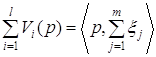
где , а скалярное произведение справа, с учетом структуры векторов , трактуется как прибыль всего производственного сектора. Заметим, что суммирование векторов осуществляется покомпонентно.

Функции спроса , и предложения , предполагаются векторными и множественнозначными. Например, для функции первое свойство означает, что , где - скалярная функция спроса на k‑ый товар. Второе свойство означает, что функция каждому p ставит в соответствие не один вектор , а множество таких векторов, т.е. . Это имеет место когда максимум спроса достигается не только в одной точке.

В модели Вальраса понятия совокупных спроса и предложения формализуются следующим образом.

Определение 2.1. Функцией совокупного (рыночного) спроса называется множественнозначная функция

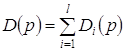(2.3)

Функцией совокупного (рыночного) предложения называется множественнозначная функция

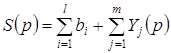(2.4)

Введем обозначения:

, ,

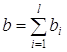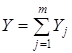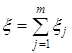
По определению, любой элемент множества Y можно представить вектором , где . Так как есть множество оптимальных планов производителя j, то компонентами вектора являются оптимальные объемы выпуска и затрат, и все они составляют решение одной и той же оптимизационной задачи. Таким образом, часть компонент вектора , как и векторов , отражает предложение готовых продуктов, а часть – спрос на первичные факторы. Поэтому вектор нельзя называть однозначно предложением. В то же время, вектор может быть интерпретирован как совокупное предложение, так как часть компонент вектора , соответствующая спросу, «компенсируется» вектором b.

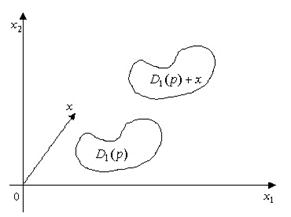
Рис. 2. Сумма вектора и множества.

Покажем, что для любого p и , т.е. областью изменения совокупных функций является то же самое пространство, что и для индивидуальных функций. Рассмотрим сначала двух потребителей. Для любого множество образуется смещением множества в направлении вектора x на длину этого вектора (рис. 2). Поэтому:

Рассмотрим трех потребителей. Для любого множество образуется смещением множества в направлении вектора x на длину этого вектора. Поэтому:

Продолжая эти рассуждения, получаем

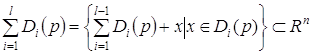
Точно так же устанавливается включение . Так как и потому , то множество b+Y образуется смещением множества Y в направлении вектора b на длину этого вектора. Поэтому .

Формализовав понятия функций совокупных спроса и предложения, модель рынка (2.1) можно представить совокупностью вида

(2.5)

Любой вектор называется совокупным спросом (соответствующим вектору цен p); любой вектор – совокупным предложением (соответствующим вектору цен p). Эти векторы являются (оптимальными) реакциями совокупного покупателя и совокупного продавца на установившийся на рынке вектор цен. Если при этом , то на рынке возникает дефицит товаров, а при появляются их излишки. Такие цены не могут считаться удовлетворительными, так как в одном случае ущемлены интересы покупателей, а в другом – продавцов. Очевидно, наилучшим вариантом для экономики является равенство . Этот идеальный случай на практике не всегда имеет место. Поэтому целесообразно как-то его ослабить. В модели Вальраса допускается наиболее «гуманный» с точки зрения интересов потребителей вариант обобщения понятия экономического равновесия.

Определение 2.2. Набор векторов называется конкурентным равновесием на рынке (2.5), если ,

, (2.6)

(2.7)

(2.8)

В этом случае p^* называется равновесным вектором цен.

По определению функций совокупных спроса и предложения, из включений (2.6) следует

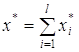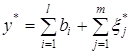, где , ;

, где , ,

т.е. совокупные спрос и предложение формируются как суммарные величины индивидуальных спросов потребителей и индивидуальных предложений производителей. Поэтому в развернутом виде условия равновесия (2.6) – (2.8) можно переписать так:

, ; (2.9)

, ; (2.10)

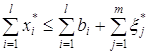(2.11)

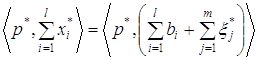(2.12)

Экономическое содержание условий, определяющих конкурентное равновесие на рынке (2.5), таково. Условие (2.6) показывает, что на цены p^* каждый потребитель и каждый производитель реагирует наилучшим образом. Это наглядно видно из соотношений (2.9) и (2.10). Условие (2.7) отслеживает, чтобы совокупное предложение не было меньше совокупного спроса. Условие (2.8) требует, чтобы в стоимостном выражении совокупный спрос равнялся совокупному предложению. Условие (2.8) автоматически выполняется в том случае, если в (2.7) имеет место строгое равенство. В этом случае равновесие будет задано соотношениями:

, , (2.13)

т.е. нужность в условии (2.8) отпадает

Предположим, что для некоторого товара в (2.7) имеет место строгое неравенство: . Тогда в стоимостном выражении получаем неравенство , не соответствующее условию (2.8). Величина называется излишком.

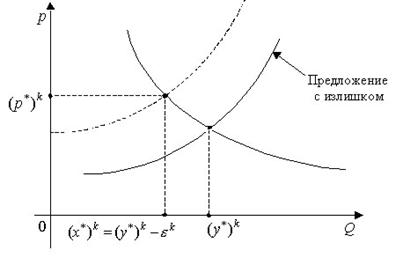
Рис. 3. Предложение с излишком

Согласно закона предложения, в случае появления излишка цена товара должна быть снижена (рис. 3.). Но это приведет к изменению «равновесной» цены . Выход из противоречия:

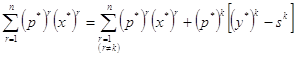
Отсюда видно, для восстановления условия (2.8) нужно «ликвидировать» излишек. С учетом знака это возможно только при . Но тогда

и

т.е. товар k вообще исключается из обращения на рынке.

Обоснование справедливости (2.8) тем, что «поставляемый сверх имеющегося спроса товар получает нулевую цену», экономически осмыслено, но не поддается адекватной формализации. Действительно, для фиксированного числа неравенство

несовместимо с равенством

Таким образом, формальный выход из рассматриваемой ситуации состоит в том, чтобы считать цену перепроизводимого товара равной нулю. Чисто теоретически этот прием состоятелен, так как не приводит в дальнейшем к противоречиям.

В то же время, следует признать отсутствие экономически осмысленного объяснения существования товара с нулевой ценой. Объявление такого товара «свободным» представляется несостоятельным. Строго говоря, в экономике нет свободных товаров, любой побочный продукт может найти применение, т.е. имеет ненулевую цену. Трудно согласиться и с «хорошо известной экономистам модификацией закона спроса и предложения о существовании перепроизводимых товаров с нулевой ценой», поскольку в случае перепроизводства «спрашиваемая» часть этого товара продается по ненулевой цене. Для экономики существование излишек так же плохо, как и существование дефицита. Все это говорит в пользу целесообразности определения равновесия в виде (2.13).

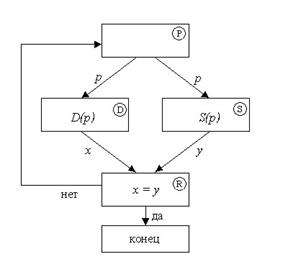
Рис. 4. Схема формирования равновесных цен

Итак, модель рынка по Вальрасу построена. Как видим, центральное место в ней занимает понятие конкурентного равновесия. Привлекательность равновесия как состояния рынка (и экономики в целом), заключается в возможности реализации всех произведенных товаров и в удовлетворении спроса всех потребителей. Процесс формирования рыночных цен условно можно сравнить с работой некоторого алгоритма (автомата), состоящего из четырех блоков (рис. 4). В первом блоке P формируется вектор цен.

Информация о векторе p поступает в блоки D и S, в которых формируются соответственно множества D(p) и S(p), содержание которых, в свою очередь, передается в блок R. В блоке R осуществляется попарное сравнение элементов , . Если существует пара или пары (x, y), для которых выполняется условие x=y (или условия (2.7), (2.8)), то процесс заканчивается. В противном случае цены p отвергаются, о чем поступает сигнал в блок P, где формируются новые цены. Процедура продолжается до тех пор, пока не будет найден равновесный вектор цен.

Утвердительный ответ на этот вопрос связан с разрешением двух важных проблем:

1. установление факта существования конкурентного равновесия в модели Вальраса;

2. разработка сходящейся к равновесной цене вычислительной процедуры (метода) формирования рыночных цен.

Существование равновесия в модели Вальраса не установлено. Причина заключается в уровне формализма этой модели – она весьма абстрактна. Конкретизируя определения составляющих ее элементов и уточняя их функциональные свойства, можно получить разные модификации модели Вальраса. Наиболее известная из них носит название модели Эрроу-Дебре, по именам ее создателей.

Проблема разработки численных методов вычисления равновесных цен связана с установлением необходимых и достаточных признаков равновесия. Нужно, чтобы они были конструктивными, т.е. порождали сходящуюся итеративную процедуру, каковой является, например, паутинообразная модель.

3. Модель Эрроу-Дебре. Существование конкурентного равновесия

Структурно модель Эрроу-Дебре весьма близка к модели Вальраса. От последней она отличается конкретизацией природы происхождения функций предложения и спроса, а также механизма образования дохода потребителя. Покажем это по порядку.

Для каждого производителя j введем множество , которое, в отличие от модели Вальраса, здесь будем трактовать как множество производственных планов (а не оптимальных планов), т.е. это есть множество n‑мерных векторов , часть компонент которых описывает затраты, а другая часть – соответствующие этим затратам выпуски товаров. Компоненты, соответствующие затратам, как и в модели Вальраса, снабжаются отрицательными знаками. Поэтому скалярное произведение показывает прибыль, полученную производителем j в результате реализации плана . Отсюда оптимальный план , участвующий в определении совокупного предложения (см. (2.3) и (2.4)), определяется как решение задачи:

при ограничении (3.1)

Оптимальное решение этой задачи обозначим через , а множество всех таких решений (множество оптимальных планов) – через . Если задача (3.1) имеет единственное решение, то, .

Доход потребителя i складывается следующим образом. Вводится коэффициент , который показывает долю i‑го потребителя в прибыли j‑го производителя. Предполагается (как и в модели Вальраса), что прибыль каждого производителя делится между всеми потребителями полностью, т.е. для любого j=1,…, m

,

Пользуясь коэффициентами , суммарные дивиденды , получаемые потребителем i от производственного сектора, можно представить как

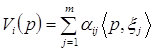
где . Поэтому общий доход потребителя i при реализации производственных планов , j=1,…, m, вычисляется по формуле

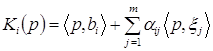
Функция спроса потребителя конкретизируется следующим образом. Вводится множество допустимых векторов потребления , а предпочтение потребителя на этом множестве задается с помощью функции полезности . В результате вектор-функция спроса строится как решение задачи:

при ограничениях , (3.2)

Оптимальное решение этой задачи обозначим через , а множество всех таких решений – через . Если задача (3.2) имеет единственное решение, то .

Таким образом, очерчены конкретные виды множеств в правых частях соотношений (2.3) и (2.4), определяющих функции совокупных спроса и предложения:

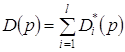(3.3)

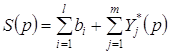(3.4)

Модель (2.5), в которой функции и определены в виде (3.3) и (3.4), называется моделью Эрроу-Дебре, если выполнены следующие требования.

У‑1. Множество компактно в и содержит нулевой вектор (j=0,…, m).

У‑2. Множество 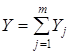выпукло в .

У‑3. Множество замкнуто и выпукло в и таково, что из , для некоторого r, следует для всех k=1,…, n (i=1,…, l).

У‑4. Функция полезности непрерывно дифференцируема на и строго вогнута (i=1,…, l).

У‑5. Функция обладает свойством ненасыщаемости (i=1,…, l).

У‑6. Существует , для которого (i=1,…, l).

Условие У‑1, с учетом непрерывности функции прибыли, обеспечивает существование решения задачи (3.2). Условие У‑2 допускает эффективность использования «смешанных» планов производства на уровне всего производственного сектора. Условия У‑3 и У‑4 имеют технический характер. Условие У‑6 требует наличия у каждого потребителя «существенного» начального запаса всех товаров. Оно считается достаточно жестким, но без него (или незначительного его ослабления) нельзя доказать существование конкурентного равновесия в модели Эрроу-Дебре (см. замечание после доказательства теоремы 3.1).

Прежде чем приступить к доказательству теоремы, разъясню несколько терминов и сформулирую вспомогательные утверждения.

Пусть , а F – множественнозначное отображение, которое переводит каждую точку в некоторое подмножество множества X (, ).

Отображение F называется полунепрерывным сверху, если из соотношений , где , и , где , следует . Другими словами, для каждого открытого множества U, содержащего множество , можно найти такое число , что , как только (где – расстояние между точками и ).

Непрерывное отображение всегда полунепрерывно сверху, а обратное неверно. Чтобы полунепрерывное сверху отображение было непрерывным, нужно, чтобы оно было одновременно полунепрерывным снизу, т.е. для каждого при существовали такие , что .

Отображение F называется ограниченным, если для любого множество F(x) является ограниченным, как подмножество евклидова пространства .

Лемма 3.1. Пусть P, X – выпуклые и компактные подмножества пространства , – такое множественнозначное отображение, что для любого множество B(p) есть непустой выпуклый компакт. Тогда множественнозначное отображение , такое, что

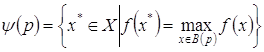
полунепрерывно сверху, если функция непрерывна и вогнута.

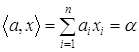Пусть , . Линейное уравнение называется гиперплоскостью в (или (n‑1) – мерным линейным многообразием). Это есть обобщение понятия обычной плоскости в . Гиперплоскость делит все пространство на две части: и .

Пусть . Говорят, что гиперплоскость разделяет X и Y, если для всех , а для всех . Например, если X и Y – выпуклые множества, не имеющие общих точек, то, очевидно, между ними существует разделяющая гиперплоскость.

Лемма 3.2. Пусть – выпуклое множество, не имеющее общих точек с неотрицательным ортантом