Скачать

Может ли энергия быть отрицательной?

Н.К. Гладышева, ИОСО РАО, школа № 548, г. Москва

Этот вопрос в так называемых стабильных учебниках никогда специально подробно не рассматривался. Считалось, что он слишком сложен для учеников средней школы. В то же время «по умолчанию» ученики (да нередко и учителя) полагают, что энергия может быть только положительной величиной. Это приводит к недоразумениям при анализе преобразования энергии в различных процессах. Например, как объяснить, что при кипячении воды вся сообщаемая веществу энергия идет на испарение, при этом средняя кинетическая энергия движения частиц не меняется, а энергия взаимодействия частиц становится равной нулю? Куда же исчезает энергия, поступающая от нагревателя? Таких примеров можно привести много. Но целесообразнее не умалчивать, что энергия взаимодействия тел может быть как положительной, так и отрицательной. Трудности в понимании этого положения надуманные. Ведь даже ученики начальных классов понимают, что температура окружающего воздуха может быть как положительной, так и отрицательной величиной! Более того, школьники достаточно легко воспринимают существование наряду со шкалой Кельвина других температурных шкал (Цельсия, Фаренгейта, Реомюра). Таким образом, идея, что численное значение какой-то физической величины зависит от условно выбираемого начала ее отсчета, не является непостижимой для старшеклассника.

Выбор начала отсчета потенциальной энергии

Покажем, как объяснить ученикам, что при изучении механических явлений во многих случаях удобно выбрать уровень отсчета потенциальной энергии так, что она будет иметь отрицательное значение.

Анализ преобразования энергии подразумевает более детальное знакомство учащихся с ее формами. В любом учебнике сообщается, что тело массой m, движущееся относительно выбранной системы отсчета с какой-то скоростью v, обладает в этой системе кинетической энергией Eкин = mv2/2. Если же в какой-то системе отсчета тело неподвижно, то его кинетическая энергия равна нулю. Поэтому кинетическую энергию тела называют энергией движения. В отличие от других характеристик движения, таких, как скорость v или импульс p = mv, кинетическая энергия не связана с направлением движения. Она является скалярной величиной. Целесообразно предложить ученикам самостоятельно показать, что кинетическая энергия тела и системы тел не может быть отрицательной величиной.

Природа потенциальной энергии может быть совершенно различной. В случае с математическим маятником (материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l) она связана с притяжением груза маятника Землей. Именно это гравитационное взаимодействие уменьшает скорость груза при его движении вверх. В случае с теннисным мячом, ударяющимся о стенку, потенциальная энергия связана с деформацией мяча. Общее же у энергии взаимодействия груза с Землей и энергии деформации то, что такая энергия может преобразовываться в кинетическую энергию и обратно.

Однако далеко не все процессы обратимы. Например, при ударе молотка по кусочку свинца кинетическая энергия молотка вроде бы исчезает бесследно – молоток почти не отскакивает после удара. В данном случае происходит преобразование кинетической энергии молотка в теплоту и последующая ее необратимая диссипация.

Подробнее рассмотрим понятие потенциальной энергии. Природа потенциальной энергии различна, поэтому нет единой формулы для ее вычисления. Из всех видов взаимодействия мы чаще всего встречаемся с гравитационным взаимодействием Земли и тел, находящихся вблизи ее поверхности, поэтому в первую очередь следует остановиться на обсуждении особенностей гравитационного взаимодействия.

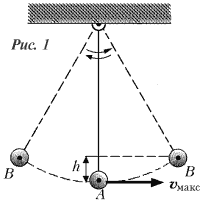
Какова формула для расчета потенциальной энергии взаимодействия Земли с находящимися вблизи ее поверхности телами? Ответ подсказывают колебания маятника. Обратите внимание (рис. 1): точки В, в которых кинетическая энергия полностью преобразуется в скрытую (потенциальную) форму, и точка А,

где кинетическая энергия маятника полностью восстанавливается, лежат на разной высоте над поверхностью Земли. Еще Гюйгенс выяснил, что высота h подъема маятника до точки В пропорциональна квадрату его скорости v2макс в нижней точке А. Лейбниц оценивал величину скрытой (потенциальной) энергии в точках В по массе m груза маятника и высоте h его подъема при колебаниях. Точные измерения максимальной скорости vмакс и высоты h показывают, что всегда выполняется равенство:

где g  10 Н/кг = 10 м/с2. Если в соответствии с законом сохранения энергии считать, что вся кинетическая энергия маятника преобразуется в точках В в энергию гравитационного взаимодействия его груза с Землей, то энергию этого взаимодействия нужно рассчитывать по формуле:

Еп = mgh.

В этой формуле скрыто условное соглашение: положение взаимодействующих тел, при котором энергия их взаимодействия Еп условно считается равной нулю (нулевой уровень), выбирается так, что в этом положении высота h = 0. Но при выборе нулевого уровня физики руководствуются только стремлением предельно упростить решение задачи. Если по каким-то соображениям удобно считать, что потенциальная энергия равна нулю в точке на высоте h0  0, то формула для потенциальной энергии принимает вид:

Еп = mg(h – h0).

Рассмотрим падение камня со скалы (рис. 2). Необходимо определить, как изменяется кинетическая энергия Ек камня и потенциальная энергия Еп его взаимодействия с Землей по мере падения. Предположим, что на краю скалы (точка А) скорость камня равна нулю.

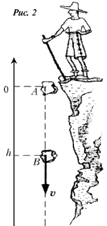
При падении камня его трение о воздух невелико, поэтому можно считать, что нет диссипации энергии и перехода ее в теплоту. Следовательно, согласно закону сохранения энергии при падении камня не меняется сумма кинетической и потенциальной энергии системы тел Земля + камень, т.е.

(Ек + Еп)|B = (Ек+Е0)|A.

Отметим следующее.

1. Согласно условию задачи в точке А скорость камня равна нулю, поэтому Ек| A = 0.

2. Нулевой уровень потенциальной энергии взаимодействия камня с Землей удобно выбрать так, чтобы предельноупростить решение задачи. Поскольку указана только одна фиксированная точка – край скалы А, – то разумно принять ее за начало отсчета и положить Еп| A = 0. Тогда полная энергия (Ек + Еп)|A = 0. Следовательно, в силу закона сохранения энергии сумма кинетической и потенциальной энергий камня и Земли остается равной нулю во всех точках траектории:

(Ек + Еп)|B = 0.

Сумма двух ненулевых чисел равна нулю только при условии, что одно из них отрицательное, а другое – положительное. Мы уже отмечали, что кинетическая энергия не может быть отрицательной. Поэтому из равенства (Ек + Еп)|B = 0 следует, что потенциальная энергия взаимодействия падающего камня с Землей является величиной отрицательной. Это связано с выбором нулевого уровня потенциальной энергии. За нулевую точку отсчета координаты h камня мы приняли край скалы. Все точки, через которые пролетает камень, лежат ниже края скалы, и значения координат h этих точек лежат ниже нуля, т.е. они отрицательны. Следовательно, согласно формуле Еп = mgh отрицательной должна быть и энергия Еп взаимодействия падающего камня с Землей.

Из уравнения закона сохранения энергии Ек + Еп = 0 вытекает, что на любой высоте h вниз от края скалы кинетическая энергия камня равна его потенциальной энергии, взятой с обратным знаком:

Ек = –Еп = –mgh

(при этом следует помнить, что h – отрицательная величина). Графики зависимости потенциальной энергии Еп и кинетической энергии Ек от координаты h показаны на рис. 3.

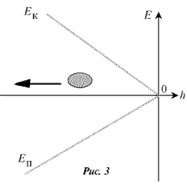
Нелишне тут же разобрать и случай, когда камень подбрасывается вверх в точке А с некоторой вертикальной скоростью v0. В начальный момент кинетическая энергия камня Eк = mv02/2, а потенциальная энергия, по соглашению, равна нулю. В произвольной точке траектории полная энергия равна сумме кинетической и потенциальной энергий mv2/2 + mgh. Закон сохранения энергии записывается в виде:

mv02/2 = mv2/2 + mgh.

Здесь h может иметь как положительные, так и отрицательные значения, что соответствует движению камня вверх от точки бросания или падению ниже точки А. Таким образом, при определенных значениях h потенциальная энергия положительна, а при других – отрицательна. Этот пример должен показать учащемуся условность приписывания потенциальной энергии определенного знака.

После знакомства учащихся с приведенным выше материалом, целесообразно обсудить с ними следующие вопросы:

1. При каком условии равна нулю кинетическая энергия тела? потенциальная энергия тела?

2. Объясните, соответствует ли закону сохранения энергии системы тел Земля + камень график на рис. 3.

3. Как меняется кинетическая энергия подброшенного мяча? Когда она уменьшается? увеличивается?

4. Почему при падении камня его потенциальная энергия оказалась отрицательной, а при скатывании мальчика с горки ее считают положительной?

Потенциальная энергия тела в гравитационном поле

Следующий шаг предполагает знакомство учеников с потенциальной энергией тела в поле тяготения. Энергия взаимодействия тела с гравитационным полем Земли описывается формулой Еп = mgh только в том случае, если гравитационное поле Земли можно считать однородным, не зависящим от координат. Гравитационное поле определяется законом всемирного тяготения:

где R – радиус-вектор, проведенный от центра масс Земли (принятого за начало отсчета) до данной точки (напомним, что в законе тяготения тела считаются точечными и неподвижными). По аналогии с электростатикой можно записать эту формулу в виде:

Fтяг = m1g,

и назвать вектором напряженности гравитационного поля в данной точке. Ясно, что это поле изменяется с расстоянием от создающего поле тела. Когда же можно считать гравитационное поле с достаточной точностью однородным? Очевидно, это возможно в области пространства, размеры которой h много меньше расстояния до центра поля R. Иными словами, если вы рассматриваете падение камня с верхнего этажа дома, можно спокойно пренебречь разницей в значении гравитационного поля на верхнем и нижнем этажах. Однако, изучая движение планет вокруг Солнца, нельзя считать, что планета движется в однородном поле, и следует пользоваться общим законом тяготения.

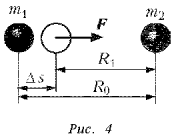
Можно вывести общую формулу потенциальной энергии гравитационного взаимодействия тел (но не просить учеников воспроизводить этот вывод, хотя окончательную формулу они, конечно, должны знать). Например, рассмотрим два точечных неподвижных тела массами m1 и m2 , расположенные на расстоянии R0 друг от друга (рис. 4). Обозначим энергию гравитационного взаимодействия этих тел через Еп0. Предположим далее, что тела немного сблизились до расстояния R1. Энергия взаимодействия этих тел стала Еп1. Согласно закону сохранения энергии:

Еп = Еп1 – Еп0 = Fтяг. ср s,

где Fтяг. cр – величина средней силы тяготения на участке s = R1 – R0 перемещения тела в направлении силы. По закону всемирного тяготения величина силы есть:

поэтому

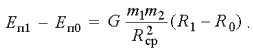
Если расстояния R1 и R0 мало отличаются друг от друга, то можно заменить расстояние Rср2 произведением R1R0. Тогда:

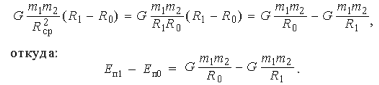
В этом равенстве Еп1 соответствует ,соответствует . Таким образом:

Мы получили формулу, которая указывает на две особенности потенциальной энергии гравитационного взаимодействия (ее еще называют энергией тяготения):

1. В самой формуле уже заложен выбор нулевого уровня потенциальной энергии тяготения, а именно: энергия гравитационного взаимодействия тел обращается в нуль, когда расстояние между рассматриваемыми телами бесконечно велико. Обратите внимание, что такой выбор нулевого значения энергии гравитационного взаимодействия тел имеет наглядную физическую интерпретацию: при бесконечно большом удалении тел друг от друга они практически перестают гравитационно взаимодействовать.

2. Поскольку любое реальное расстояние, например между Землей и ракетой, конечно, энергия гравитационного взаимодействия при таком выборе начала отсчета всегда отрицательна.

На рис. 5 приведен график зависимости энергии гравитационного взаимодействия ракеты с Землей от расстояния между центром Земли и ракетой. Он отражает обе особенности энергии тяготения, о которых мы говорили: показывает, что эта энергия отрицательна и возрастает к нулю при увеличении расстояния между Землей и ракетой.

Энергия связи

Полученные учениками знания о том, что энергия может быть как положительной, так и отрицательной величиной, должны найти свое применение при изучении энергии связи частиц вещества в разных его агрегатных состояниях. Например, школьникам можно предложить следующие качественные рассуждения.

Мы уже убедились, что частицы вещества всегда хаотично движутся. Именно наделив частицы способностью к такому движению, мы смогли объяснить целый ряд явлений природы. Но тогда почему не разлетаются на отдельные частицы столы и карандаши, стены домов и мы сами?

Приходится предположить, что частицы вещества взаимодействуют, притягиваются друг к другу. Только достаточно сильное взаимное притяжение частиц способно удерживать их друг около друга в жидкостях и твердых телах, не давать им быстро разлетаться в разные стороны. Но почему тогда не удерживаются друг около друга частицы в газах, почему они разлетаются? По-видимому, в газах взаимосвязь частиц недостаточна для их удержания.

В механике для оценки взаимодействия (связи) тел мы использовали такую физическую величину, как потенциальная энергия взаимодействия. В кинетической теории вещества связь частиц вещества характеризуется энергией их взаимодействия Есв (эта энергия не всегда потенциальная). Тот факт, что частицы в жидкости и в твердом теле удерживают друг друга, а в газах нет, подсказывает, что энергия связи частиц друг с другом в этих средах разная.

Газ. В газе расстояние между частицами велико и их связь слаба. Частицы изредка сталкиваются друг с другом и со стенками сосуда. Соударения носят упругий характер, т.е. полная энергия и полный импульс сохраняются. В промежутках между соударениями частицы движутся свободно, т.е. не взаимодействуют. Разумно считать, что энергия взаимодействия (связи) частиц в газе приближенно равна нулю.

Жидкость. В жидкости частицы сближены, они частично соприкасаются. Их взаимное притяжение велико и характеризуется энергией связи Есв(вода). Чтобы оторвать одну молекулу от основной массы жидкости, необходимо совершить работу A > 0. В результате молекула станет свободной, как в газе, т.е. ее энергию связи можно будет считать равной нулю. По закону сохранения энергии Есв(вода)+ А = 0, откуда Есв(вода) = –А < 0.

Чтобы определить численное значение энергии Есв(вода) частиц в воде, обратимся к эксперименту. Уже бытовые наблюдения подсказывают: чтобы испарить воду, кипящую в чайнике, нужно сжечь некоторое количество дров или газа. Другими словами, нужно совершить работу. С помощью термометра можно убедиться, что температура кипящей воды и температура пара над ней одинаковы. Следовательно, одинакова средняя энергия движения частиц в кипящей воде и в паре. тепловая энергия, передаваемая кипящей воде от топлива, преобразуется в энергию взаимодействия частиц испаряющейся воды. Значит, энергия Есв частиц в кипящей воде меньше, чем в водяном паре. Но в паре Есв(пар) = 0, следовательно, энергия взаимодействия частиц в жидкости меньше нуля, т.е. отрицательна.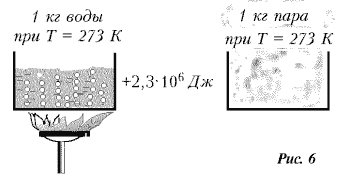

Измерения с помощью калориметров показывают, что для испарения 1 кг кипящей воды при нормальном атмосферном давлении нужно передать ей около 2,3  106 Дж энергии. Часть этой энергии (приблизительно 0,2  106 Дж) затрачивается на то, чтобы образующийся водяной пар смог вытеснить частицы воздуха из тонкого слоя над поверхностью жидкости. Остальная энергия (2,1  106 Дж) идет на увеличение энергии связи частиц воды при их переходе из жидкости в пар (рис. 6). Расчеты показывают, что в 1 кг воды содержится 3,2  1025 частиц. Поделив энергию 2,1  106 Дж на 3,2  1025, получим: энергия связи Есв каждой частицы воды с остальными частицами при ее переходе из жидкости в пар увеличивается на величину 6,6  10–20 Дж.

Твердое тело. Чтобы расплавить и превратить лед в воду, нужно совершить работу или передать льду определенное количество теплоты. Энергия связи молекул воды в твердой фазе Есв < 0, причем эта энергия по модулю больше, чем энергия связи молекул воды в жидкой фазе. При таянии льда его температура остается равной 0 °С; такую же температуру имеет и образующаяся при таянии вода. Следовательно, чтобы перевести вещество из твердого состояния в жидкое, нужно увеличить энергию взаимодействия его частиц. Чтобы растопить 1 кг уже начавшего таять льда, нужно затратить 3,3  105 Дж энергии (рис. 7). Практически вся эта энергия идет на увеличение энергии связи частиц при их переходе изо льда в воду. Поделив энергию

3,3  105 Дж на число 3,2  1025 частиц, содержащихся в 1 кг льда, найдем, что энергия Есв взаимодействия частиц льда на 10–20Дж меньше, чем в воде.

Итак, энергия взаимодействия частиц пара равна нулю. В воде энергия связи каждой ее частицы с остальными частицами приблизительно на 6,6  10–20 Дж меньше, чем в паре, т.е. Есв(вода) = –6,6  10–20 Дж. Во льду энергия связи каждой частицы со всеми остальными частицами льда на 1,0  10–20 Дж меньше, чем в воде (и соответственно на 6,6  10–20 Дж + 1,0  10–20 Дж = 7,6  10–20 Дж меньше, чем в водяном паре). Значит, во льду Есв(лед) = –7,6  10–20 Дж.

Рассмотрение особенностей энергии взаимодействия частиц вещества в различных агрегатных состояниях важна для понимания преобразования энергии при переходах вещества из одного агрегатного состояния в другое.

Приведем, в частности, примеры вопросов, на которые теперь ученики смогут ответить без особых затруднений.

1. Вода кипит при постоянной температуре, поглощая энергию от пламени газовой горелки. Что происходит при этом?

А) Увеличивается энергия движения молекул воды;

Б) увеличивается энергия взаимодействия молекул воды;

В) уменьшается энергия движения молекул воды;

Г) уменьшается энергия взаимодействия молекул воды.

(Ответ: Б.)

2.При плавлении льда:

А) увеличивается кинетическая энергия куска льда;

Б) увеличивается внутренняя энергия льда;

В) уменьшается потенциальная энергия куска льда;

Г) уменьшается внутренняя энергия льда.

(Ответ: Б.)

До сих пор мы рассматривали энергию взаимодействия тел, притягивающихся друг к другу. При изучении электростатики полезно обсудить с учениками вопрос, положительна или отрицательна энергия взаимодействия частиц, если они отталкиваются друг от друга. При взаимном отталкивании частиц нет необходимости сообщать им энергию, чтобы удалить далеко друг от друга. Энергия взаимодействия преобразуется в энергию движения разлетающихся частиц и убывает до нуля с ростом расстояния между частицами. В данном случае энергия взаимодействия – положительная величина. Выявленные особенности энергии взаимодействия можно закрепить при обсуждении таких вопросов:

1. Положительна или отрицательна энергия взаимодействия двух разноименно заряженных шариков? Обоснуйте свой ответ.

2. Положительна или отрицательна энергия взаимодействия двух одноименно заряженных шариков? Обоснуйте свой ответ.

3. Два магнита сближаются одноименными полюсами. Увеличивается или уменьшается энергия их взаимодействия?

Энергия связи в микромире

Согласно представлениям квантовой механики атом состоит из ядра, окруженного электронами. В системе отсчета, связанной с ядром, полная энергия атома складывается из энергии движения электронов вокруг ядра, энергии кулоновского взаимодействия электронов с положительно заряженным ядром и энергии кулоновского взаимодействия электронов друг с другом. Рассмотрим самый простой из атомов – атом водорода.

Считается, что полная энергия электрона равна сумме кинетической энергии и потенциальной энергии кулоновского взаимодействия с ядром. Согласно модели Бора полная энергия электрона в атоме водорода может принимать только определенный набор значений:

где Е0 выражается через мировые постоянные и массу электрона. Численные значения Е(n) удобнее измерять не в джоулях, а в электрон-вольтах. Первые разрешенные значения равны:

Е(1) = –13,6 эВ (энергия основного, наиболее устойчивого состояния электрона);

Е(2) = –3,4 эВ;

Е(3) = –1,52 эВ.

Весь ряд разрешенных значений полной энергии атома водорода удобно отмечать черточками на вертикальной оси энергий (рис. 8). Формулы для расчета возможных значений энергии электронов для атомов других химических элементов сложны, т.к. в атомах много электронов, взаимодействующих не только с ядром, но и друг с другом.

Атомы, соединяясь, образуют молекулы. В молекулах картина движения и взаимодействия электронов и атомных ядер много сложнее, чем в атомах. Соответственно меняется и усложняется набор возможных значений внутренней энергии. Возможные значения внутренней энергии любого атома и молекулы имеют некоторые особенности.

Первую особенность мы уже выяснили: энергия атома квантована, т.е. может принимать только дискретный набор значений. Атомам каждого вещества присущ собственный набор значений энергии.

Вторая особенность состоит в том, что все возможные значения Е(n) полной энергии электронов в атомах и молекулах отрицательны. Эта особенность связана с выбором нулевого уровня энергии взаимодействия электронов атома с его ядром. Принято считать, что энергия взаимодействия электрона с ядром равна нулю, когда электрон удален на большое расстояние и кулоновское притяжение электрона к ядру пренебрежимо мало. Но, чтобы полностью оторвать электрон от ядра, нужно затратить некоторую работу, передать ее системе ядро + электрон. Другими словами, чтобы энергия взаимодействия электрона с ядром стала равной нулю, ее нужно увеличить. А это и означает, что исходная энергия взаимодействия электрона с ядром меньше нуля, т.е. отрицательна.

Третья особенность в том, что сделанные на рис. 8 отметки возможных значений внутренней энергии атома обрываются при Е = 0. Это не означает, что энергия системы электрон + ядро в принципе не может быть положительной. Но когда она достигает нулевого значения, система перестает быть атомом. Ведь при значении Е = 0 электрон удален от ядра, и вместо атома водорода существуют не связанные друг с другом электрон и ядро.

Если оторвавшийся электрон продолжает двигаться с кинетической энергией Ек, то и суммарная энергия системы уже не взаимодействующих частиц ион + электрон может принимать любые положительные значения Е = 0 + Ек.

Вопросы для обсуждения

1. Из каких слагаемых складывается внутренняя энергия атома?

2. Почему мы рассматривали энергию атома только на примере атома водорода?

3. Какие выводы об особенностях внутренней энергии атома вытекают из его квантовомеханической модели?

4. Почему мы считаем внутреннюю энергию атома или молекулы отрицательной?

5. Может ли энергия группы ион + электрон быть положительной?

Знакомство с внутренней энергией атома позволит не только закрепить знания о возможности отрицательных значений потенциальной энергии, но и объяснить ряд явлений, например явление фотоэффекта или излучение света атомами. Наконец, полученные знания позволят обсудить с учениками очень интересный вопрос о взаимодействии нуклонов в ядре.

Установлено, что атомное ядро состоит из нуклонов (протонов и нейтронов). Протон – частица массой в 2000 раз больше массы электрона, несущая положительный электрический заряд (+1). Как известно из электродинамики, заряды одинакового знака взаимно отталкиваются. Следовательно, электромагнитное взаимодействие расталкивает протоны. Почему же ядро не разваливается на составные части? Еще в 1919 г., обстреливая ядра -частицами, Э.Резерфорд выяснил: чтобы выбить протон из ядра, -частица должна иметь энергию около 7 МэВ. Это в несколько сот тысяч раз больше энергии, необходимой для отрыва электрона от атома!

В результате многочисленных экспериментов было установлено, что частицы внутри ядра связаны принципиально новым видом взаимодействия. Его интенсивность в сотни раз превосходит интенсивность электромагнитного взаимодействия, поэтому его назвали сильным взаимодействием. Это взаимодействие обладает важной особенностью: оно имеет малый радиус действия и «включается» только тогда, когда расстояние между нуклонами не превышает 10–15 м. Этим объясняются небольшие размеры всех атомных ядер (не более 10–14 м).

Протонно-нейтронная модель ядра позволяет рассчитать энергию связи нуклонов в ядре. Напомним, что согласно измерениям она приблизительно равна –7 МэВ. Представим себе, что 4 протона и 4 нейтрона объединились, образовав ядро бериллия. Масса каждого нейтрона mn = 939,57 МэВ, а масса каждого протона mp = 938,28 МэВ (здесь мы используем принятую в ядерной физике систему единиц, в которой масса измеряется не в килограммах, а в эквивалентных энергетических единицах, пересчитанных по соотношению Эйнштейна Е0 = mc2). Следовательно, суммарная энергия покоя 4 протонов и 4 нейтронов до их объединения в ядро составляет 7511,4 МэВ. Энергия покоя ядра Ве составляет 7454,7 МэВ. Ее можно представить как сумму энергии покоя самих нуклонов (7511,4 МэВ) и энергии связи нуклонов друг с другом Есв. Поэтому:

7454,7 МэВ = 7511,4 МэВ + Есв.

Отсюда получаем:

Еп= 7454,7 МэВ –7511,4 МэВ = –56,7 МэВ.

Эта энергия распределяется на все 8 нуклонов ядра бериллия. Следовательно, на каждый из них приходится примерно –7 МэВ, что и следует из экспериментов. Мы вновь получили, что энергия связи взаимно притягивающихся частиц является отрицательной величиной.