Скачать

Моделювання оптимального розподілу інвестицій за допомогою динамічного програмування

Українська академія банківської справи

Національного банку України

Кафедра економічної кібернетики

КУРСОВА РОБОТА

з дисципліни «Моделювання економічної динаміки»

«Моделювання оптимального розподілу інвестицій за допомогою динамічного програмування»

Виконала: студентка 5-го курсу

групи ЕК-21

Бабенко Т.М.

Нормоконтроль: канд. фіз.-мат. наук Братушка С.М

Перевірила: ас. Хайлук С.О.

ЗМІСТ

Вступ

1. Теоретичні аспекти математичного моделювання динамічних систем

1.1 Основні поняття теорії моделювання

1.2 Принципи моделювання динамічних систем

1.3 Моделі і методи прийняття управлінських рішень з урахуванням фактору часу

1.4 Моделі динамічного програмування

2. Теоретичні аспекти динамічного програмування

2.1 Постановка задачі динамічного програмування. Основні умови й область застосування

2.2 Складання математичної моделі динамічного програмування

2.3 Етапи рішення задачі динамічного програмування

3. Оптимальний розподіл інвестицій, як задача динамічного програмування

Висновки

Список використаної літератури

Додатки

ВСТУП

Дана курсова робота присвячена вивченню методології динамічного програмування. Необхідність такого вивчення обґрунтована насамперед тим, що у ряді реальних економічних і виробничих завдань необхідно враховувати зміну моделюємого процесу в часі й вплив часу на критерій оптимальності. Для рішення зазначених завдань використається метод динамічного планування (динамічне програмування). Цей метод більш складний у порівнянні з методами зі статичних оптимізаційних задач. Також не простою справою є процес побудови для реальної задачі математичної моделі динамічного програмування.

Динамічне програмування – розділ математики, який присвячено теорії і методам розв’язання багатокрокових задач оптимального керування.

У динамічному програмуванні для керованого процесу серед множини усіх допустимих керувань шукають оптимальне у сенсі деякого критерію тобто таке яке призводить до екстремального (найбільшого або найменшого) значення цільової функції – деякої числової характеристики процесу. Під багатоступеневістю розуміють або багатоступеневу структуру процесу, або розподілення керування на ряд послідовних етапів (ступенів, кроків), що відповідають, як правило, різним моментам часу. Таким чином, в назві “Динамічне програмування” під “програмуванням” розуміють “прийняття рішень”, “планування”, а слово “динамічне” вказує на суттєве значення часу та порядку виконання операцій в процесах і методах, що розглядаються.

Методи динамічного програмування використовуються не лише в дискретних, але і в неперервних керованих процесах, наприклад, в таких процесах, коли в кожен момент певного інтервалу часу необхідно приймати рішення.

У даній роботі розглядаються теоретичні аспекти математичного моделювання динамічних систем, основні поняття теорії моделювання, принципи моделювання динамічних систем, моделі і методи прийняття управлінських рішень з урахуванням фактору часу, а також моделі динамічного програмування. Детально вивчаються процес постановки задачі динамічного програмування і особливості складання математичної моделі динамічного програмування.

Метою даної курсової роботи є вивчення методології динамічного програмування і проведення автоматизації розподілу інвестицій. Об’єктом практичного дослідження виступає розподіл інвестицій між підприємствами, а предметом дослідження є методика динамічного програмування, котра забезпечить оптимальний розподіл інвестицій.

1. ТЕОРЕТИЧНІ АСПЕКТИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ ДИНАМІЧНИХ СИСТЕМ

1.1 Основні поняття теорії моделювання

У прикладних областях розрізняють наступні види абстрактних моделей:

а) традиційне (насамперед для теоретичної фізики, а також механіки, хімії, біології, ряду інших наук) математичне моделювання без якої-небудь прив’язки до технічних засобів інформатики;

б) інформаційні моделі й моделювання, що мають додатки в інформаційних системах;

в) вербальні (тобто словесні, текстові) язикові моделі;

г) інформаційні (комп’ютерні) технології, які треба ділити:

1) на інструментальне використання базових універсальних програмних засобів (текстових редакторів, СУБД, табличних процесорів, телекомунікаційних пакетів);

2) на комп’ютерне моделювання, що представляє собою:

- обчислювальне (імітаційне) моделювання;

- “візуалізацію явищ і процесів” (графічне моделювання);

- “високі” технології, що розуміють як спеціалізовані прикладні технології, що використають комп’ютер (як правило, у режимі реального часу) у сполученні з вимірювальними апаратурами, датчиками, сенсорами й т.д.

Отже, укрупнена класифікація абстрактних (ідеальних) моделей така:

а) Вербальні (текстові) моделі. Ці моделі використають послідовності пропозицій на формалізованих діалектах природної мови для опису тієї або іншої області дійсності (прикладами такого роду моделей є міліцейський протокол, правила дорожнього руху).

б) Математичні моделі – дуже широкий клас знакових моделей (заснованих на формальних мовах над кінцевими алфавітами), що широко використає ті або інші математичні методи. Наприклад, можна розглянути математичну модель зірки. Ця модель буде являти собою складну систему рівнянь, що описують фізичні процеси, що відбуваються в надрах зірки. Математичною моделлю іншого роду є, наприклад, математичні співвідношення, що дозволяють розрахувати оптимальний (найкращий з економічної точки зору) план роботи якого-небудь підприємства.

в) Інформаційні моделі – клас знакових моделей, що описують інформаційні процеси (виникнення, передачу, перетворення й використання інформації) у системах найрізноманітнішої природи.

Границя між вербальними, математичними й інформаційними моделями може бути проведена досить умовно; цілком можливо вважати інформаційні моделі підкласом математичних моделей. Однак, у рамках інформатики як самостійної науки, відділеної від математики, фізики, лінгвістики й інших наук, виділення інформаційних моделей в окремий клас є доцільним.

Існують й інші підходи до класифікації абстрактних моделей; загальноприйнята точка зору тут ще не встановилася. Зокрема, є тенденція різкого розширення змісту поняття “інформаційна модель”, при якому інформаційне моделювання містить у собі й вербальні, і математичні моделі.

Математична модель виражає істотні риси об’єкта або процесу мовою рівнянь й інших математичних засобів. Власне кажучи, сама математика зобов’язана своїм існуванням тому, що вона намагається відбити, тобто промоделювати, на своїй специфічній мові закономірності навколишнього світу.

Шлях математичного моделювання в наш час набагато більш всеосяжний, ніж моделювання натурного. Величезний поштовх розвитку математичного моделювання дало поява ЕОМ, хоча сам метод зародився одночасно з математикою тисячі років тому.

Математичне моделювання динамічних систем, як таке, аж ніяк не завжди вимагає комп’ютерної підтримки. Кожен фахівець, що професійно займається математичним моделюванням, робить все можливе для аналітичного дослідження моделі. Аналітичні рішення (тобто представлені формулами, що виражають результати дослідження через вихідні дані) звичайно зручніші й інформативніші чисельних. Можливості аналітичних методів рішення складних математичних завдань, однак, дуже обмежені й, як правило, ці методи набагато складніше чисельних. На рисунку 1 представлена процес математичного моделювання з використанням комп’ютерної техніки.

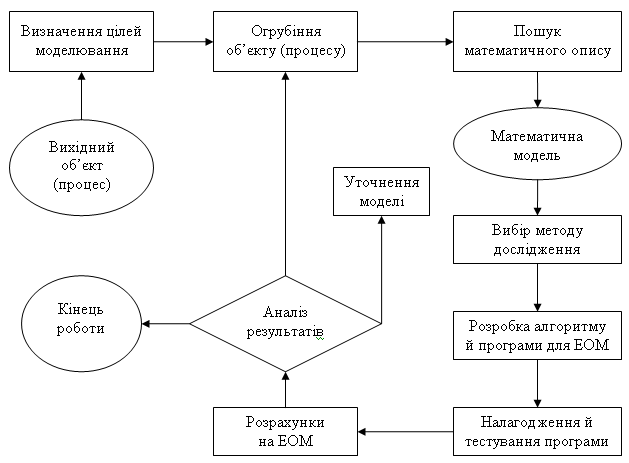
Рисунок 1.1 – Загальна схема процесу комп’ютерного математичного моделювання

Найважливішим етапом моделювання динамічних систем є поділ вхідних параметрів за ступенем важливості впливу їхніх змін на вихідні. Такий процес називається ранжируванням (поділом по рангах). Найчастіше неможливо (та й не потрібно) ураховувати всі фактори, які можуть вплинути на значення величин, що цікавлять, . Від того, наскільки вміло виділені найважливіші фактори, залежить успіх моделювання, швидкість й ефективність досягнення мети. Виділити більш важливі (або значимі) фактори й відсіяти менш важливі може лише фахівець у тій предметній області, до якої відноситься модель.

1.2 Принципи моделювання динамічних систем

інвестиція моделювання динамічний програмування

Розглядаються основні принципи моделювання динамічних систем, у стислій формі відображаючи той достатньо багатий досвід, що накопичений до теперішнього часу в області розробки й використання математичних моделей динамічних систем.

– Принцип інформаційної достатності. При повній відсутності інформації про досліджувану систему побудова її моделі неможлива. При наявності повної інформації її моделювання позбавлене змісту. Існує деякий критичний рівень апріорних відомостей про систему (рівень інформаційної достатності), при досягненні якого може бути побудована її адекватна модель.

– Принцип здійсненності. Створювана модель повинна забезпечувати досягнення поставленої мети дослідження з імовірністю, що істотно відрізняється від нуля, і за кінцевий час. Звичайно задають деяке граничне значення  імовірності досягнення цілі моделювання , а також прийнятну границю  часу досягнення цієї мети. Модель вважають здійсненною, якщо може бути виконана умова .

– Принцип множинності моделей. Даний принцип, незважаючи на його місцезнаходження у даній класифікації, є ключовим. Мова йде про те, що створювана модель повинна відбивати в першу чергу ті властивості реальної системи (або явища), які впливають на обраний показник ефективності. Відповідно при використанні будь-якої конкретної моделі визнаються лише деякі сторони реальності. Для більш повного її дослідження необхідний ряд моделей, що дозволяють із різних сторін і з різним ступенем детальності відбивати розглянутий процес.

– Принцип агрегування. У більшості випадків складну систему можна представити такою, що складається з агрегатів (підсистем), для адекватного математичного опису яких виявляються придатними деякі стандартні математичні схеми. Принцип агрегування дозволяє, крім того, досить гнучко перебудовувати модель залежно від завдань дослідження.

– Принцип параметризації. У ряді випадків система, що моделюється, має у своєму складі деякі відносно ізольовані підсистеми, що характеризуються певним параметром, у тому числі векторним. Такі підсистеми можна заміняти в моделі відповідними числовими величинами, а не описувати процес їхнього функціонування. При необхідності залежність значень цих величин від ситуації може задаватися у вигляді таблиці, графіка або аналітичного вираження (формули). Принцип параметризації дозволяє скоротити обсяг і тривалість моделювання. Однак треба мати на увазі, що параметризація знижує адекватність моделі (7).

1.3 Моделі і методи прийняття управлінських рішень з урахуванням фактору часу

При прийнятті рішень в практиці управління постає питання про задачу прийняття рішень з урахуванням фактору часу. Задача прийняття рішень спрямована на визначення найкращого (оптимального) або сприятливого способу дій для досягнення однієї або декількох цілей. Під ціллю розуміється в широкому значенні ідеальне уявлення бажаного стану чи результату діяльності. Бажаний стан чи результат для особи, що приймає рішення може означати прибуток фірми, заволодіння долею ринку, подолання конкурентної боротьби, зниження собівартості продукції тощо. Найчастіше у житті трапляється так, що бажаний стан дещо віддалений або взагалі відсутній і той стан який існує в конкретний момент прийнято називати фактичним станом, тобто тим, що не залежить від волі особи, яка приймає рішення (ОПР). Отже, якщо фактичний стан не відповідає бажаному стану, то має місце проблемна ситуація, або проблема, розробка плану подолання якої і складає сутність задачі прийняття рішень.

Проблемна ситуація може виникати за умов коли:

а) функціонування управлінської системи в певний момент часу не забезпечує досягнення бажаних цілей організації;

б) функціонування цієї системи не може забезпечити досягнення цих цілей і в майбутньому;

в) система вимагає докорінних змін поставлених цілей.

Виявлення проблемної ситуації являє собою перший етап процесу прийняття рішень. Процес прийняття управлінських рішень з урахуванням фактору часу складається з наступних етапів, котрі зображенні на рисунку 1.2.

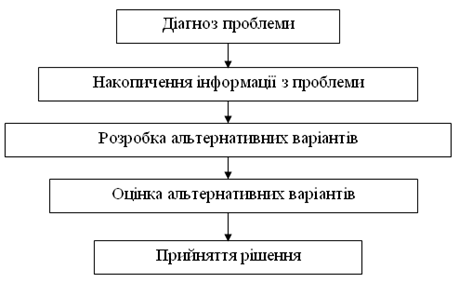
Рисунок 1.2 – Етапи процесу прийняття управлінських рішень з урахуванням фактору часу

Другий етап процесу прийняття рішень – це накопичення інформації з проблеми, а саме збирання відомостей щодо проблеми, яка вирішується. На третьому етапі при опрацюванні альтернатив потрібно враховувати такі вимоги як взаємовиключність альтернатив та забезпечення однакових умов описування альтернатив. Для виконання четвертого етапу – оцінки альтернатив, необхідно відповісти на наступні питання:

– Чи є альтернатива реалістичною?

– Чи відповідає альтернатива можливостям організації?

– Чи є прийнятними наслідки реалізації альтернативи?

Тепер, коли описані всі етапи процесу прийняття рішень, слід визначити саме поняття прийняття рішення: прийняття рішення – це порівняння альтернатив за очікуваними ефектами їх реалізації на закладі критеріїв етапу діагнозу проблеми і прийняття остаточного рішення.

Кінцевим результатом задачі прийняття рішень з урахуванням фактору часу являється рішення. Із змістовної точки зору рішенням може бути курс дії, спосіб дії, план роботи, варіант проекту тощо. Рішення являється одним з видів розумової діяльності і волевиявлення людини.

Слід зазначити, що не кожен метод може застосовуватись в будь-якій ситуації. Тобто кожне рішення або кожна задача прийняття рішення з урахуванням фактору часу може вирішуватися в різних умовах. Для визначення цих умов слід провести класифікацію задач прийняття рішень за різними ознаками (ступінь визначеності інформації, зміст рішень, направленість рішень тощо), серед яких найбільше цікавить ступінь визначеності інформації – ступінь повноти і достовірності даних, необхідних для прийняття рішень. За ступенем повноти визначеності інформації задачі прийняття рішень класифікують на три групи:

– задачі в умовах визначеності;

– задачі в умовах імовірнісної визначеності;

– задачі в умовах невизначеності.

Отже, для кожної групи умов в практиці управління використовуються та чи інша методологія.

Прийняття рішень в умовах визначеності проводяться при наявності повної і достовірної інформації щодо проблемної ситуації, умов рішень і наслідках його реалізації. Для даного класу задач прийняття рішень немає необхідності довизначати проблемну ситуацію гіпотетичними ситуаціями. Цілі і обмеження формально визначаються у вигляді цільових функцій. Критерій вибору обирається у вигляді мінімуму або максимуму цільової функції. Наявність переліченої інформації дозволяє побудувати формальну математичну модель задачі прийняття рішень і здійснити знаходження оптимального рішення алгоритмічним шляхом без втручання людини. Для вирішення цього класу задач прийняття рішень застосовуються різні методи оптимізації, наприклад, методи математичного програмування: лінійного, нелінійного, динамічного.

Задачі прийняття рішень в умовах невизначеності безпосередньо пов’язані з управлінськими рішеннями. Для цих задач характерна більша неповнота і недостовірність інформації, різноманіття і складність впливу різних факторів соціального, економічного, політичного та іншого характеру. Ці обставини не дозволяють, по крайній мірі в теперішній час, побудувати адекватні математичні моделі вирішення задач по визначенню оптимального рішення. Тому активну роль в пошуку оптимального або сприятливого рішення виконує людина.

Математичні моделі, що розглядаються в задачах прийняття рішень в умовах визначеності та імовірнісної визначеності, описують найпростіші ситуації, характерні для функціонування технічних систем. Тому задачі даного класу широко застосовуються для синтезу управління в автоматичних системах і мають дуже посереднє відношення до задач прийняття управлінських рішень в організаційних системах.

Згідно зі схемою, котра зображена на рисунку 1.3, методи обґрунтування управлінських рішень підрозділяються на дві основні групи: кількісні та якісні методи. До якісних методів відносяться лише експертні методи, а решта методів (класифікація за ступенем визначеності) відноситься до кількісних. Аналітичні методи характеризуються тим, що встановлюють аналітичні (функціональні) залежності між умовами вирішення задач прийняття рішень та їх результатами.

Статистичні методи. Їх характерною рисою є врахування випадкових впливів та відхилень. Ці методи дозволяють отримувати з накопичуваної інформації, яка здається хаотичною, основні тенденції та закономірності. Ця група охоплює методи теорії ймовірностей та математичної статистики. Найбільш широко використовуються такі методи, як кореляційний аналіз, факторний аналіз, дисперсійний аналіз, методи статистичного контролю якості та надійності продукції.

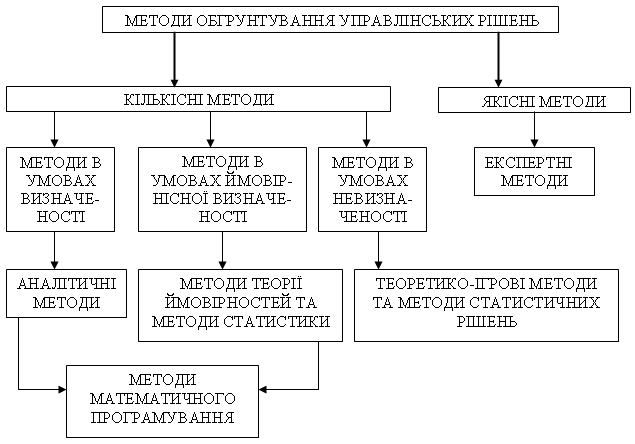
Рисунок 1.3 – Схема методів обґрунтувань управлінських рішень

Методи математичного програмування. Застосовуються при рішенні умовних екстремальних задач з багатьма змінними.

Теоретико-ігрові методи та методи статистичних рішень. Теорія статистичних рішень використовується, коли невизначеність ситуації викликана об’єктивними обставинами, які або невідомі, або носять випадковий характер. Метод теорії ігор використовується в тих випадках, коли невизначеність ситуації викликана свідомими діями розумного противника.

1.4 Моделі динамічного програмування

Модель є образним представленням якогось об’єкту чи процесу і використовується для аналізу або вивчення цього об’єкту чи процесу.

Моделі математичного програмування – це так звані одноетапні моделі, які допомагають аналізувати статичні, не залежні від часу умови. Вони мають оптимальний розв’язок за умов стабільності господарського процесу, або на короткий проміжок у майбутньому.

Вперше математичні моделі були використані для рішення практичного завдання в 30-х роках у Великобританії при створенні системи протиповітряної оборони. Для розробки даної системи були залучені вчені різних спеціальностей. Система створювалася в умовах невизначеності щодо можливих дій супротивника, тому дослідження проводилися на адекватних математичних моделях. У цей час вперше був застосований термін: “операційне дослідження”, що припускало дослідження воєнної операції. У наступні роки операційні дослідження або дослідження операцій розвиваються як наука, результати якої застосовуються для вибору оптимальних рішень при керуванні реальними процесами й системами.

Можна виділити наступні основні етапи операційного дослідження:

- спостереження явища й збір вихідних даних;

- постановка задачі;

- побудова математичної моделі;

- розрахунок моделі;

- тестування моделі й аналіз вихідних даних. Якщо отримані результати не задовольняють дослідника, то треба або повернутися на етап побудови математичної моделі, тобто запропонувати для рішення задачі іншу математичну модель; або повернутися на етап постановки задачі, тобто поставити задачу більш коректно;

- застосування результатів досліджень.

Таким чином, операційне дослідження є ітераційним процесом, кожен наступний крок якого наближає дослідника до рішення стоячої перед ним проблеми. У центрі операційного дослідження знаходяться побудова й розрахунок математичної моделі.

Математична модель – це система математичних співвідношень, приблизно, в абстрактній формі описуючі досліджуваний процес або систему. Математична модель – абстракція реальної дійсності, в якій відношення між реальними елементами, а саме ті, що цікавлять дослідника, замінені відношенням між математичними категоріями. Економіко-математична модель – це математична модель, призначена для дослідження економічної проблеми.

Проведення операційного дослідження, побудова й розрахунок математичної моделі динамічного програмування дозволяють проаналізувати ситуацію й вибрати оптимальні рішення по керуванню нею або обґрунтувати запропоновані рішення. Застосування математичних моделей динамічного програмування необхідно в тих випадках, коли проблема складна, залежить від великої кількості факторів, що по-різному впливають на її рішення. У цьому випадку непродумане й науково не обґрунтоване рішення може привести до серйозних наслідків. Прикладів цьому в нашому житті є чимало, зокрема в економіці. Використання математичних моделей динамічного програмування дозволяє здійснити попередній вибір оптимальних або близьких до них варіантів рішень за певними критеріями. Вони науково обґрунтовані, і особа, що приймає рішення, може керуватися ними при виборі остаточного рішення. Варто розуміти, що не існує рішень, оптимальних “взагалі”. Будь-яке рішення, отримане при розрахунку математичної моделі динамічного програмування, оптимально по одному або декількох критеріях, запропонованим постановником завдання й дослідником. До речі, практика показує, що займатися операційними дослідженнями й побудовою математичних моделей динамічного програмування найкраще не “чистим” математикам, що не завжди представляють собі сутність досліджуваної проблеми й приділяють більшу увагу різним математичним особливостям побудови й розрахунку, і не предметникам, які не завжди можуть коректно поставити завдання. Гарні результати одержують фахівці, що знають предметну область і разом з тим володіючи математичними методами дослідження у динамічному програмуванні. У теперішній час математичні моделі динамічного програмування застосовуються для аналізу, прогнозування й вибору оптимальних рішень у різних галузях економіки. Це планування й оперативне керування виробництвом, управління трудовими ресурсами, управління запасами, розподіл ресурсів, планування й розміщення об’єктів, керівництво проектом, розподіл інвестицій і т.п.

Можна виділити наступні основні етапи побудови математичної моделі динамічного програмування.

а) Визначення мети, тобто чого хочуть домогтися, вирішуючи поставлене завдання.

б) Визначення параметрів моделі, тобто заздалегідь відомих фіксованих факторів, на значення яких дослідник не впливає.

в) Формування керуючих змінних, змінюючи значення яких можна наближатися до поставленої мети. Значення керуючих змінних є рішеннями задачі.

г) Визначення області припустимих рішень, тобто тих обмежень, котрим повинні задовольняти керуючі змінні.

д) Виявлення невідомих факторів, тобто величин, які можуть змінюватись випадковим або невизначеним чином.

е) Вираження мети через керуючі змінні, параметри й невідомі фактори, тобто формування цільової функції, котра називається також критерієм ефективності або критерієм оптимальності задачі.

Вводяться наступні умовні позначки:  – параметри моделі;  – керуючі змінні або рішення; – область припустимих рішень;  – випадкові або невизначені фактори;  – цільова функція або критерій ефективності (критерій оптимальності).

.                                                                                          (1.1)

У відповідність із введеними термінами математична модель задачі має наступний вигляд:

,                                                            (1.2)

Вирішити задачу – це значить знайти таке оптимальне рішення , щоб при даних фіксованих параметрах  й з урахуванням невідомих факторів  значення критерію ефективності  було б по можливості максимальним (мінімальним).

.                                                    (1.3)

Таким чином, оптимальне рішення – це рішення, краще перед іншими за певним критерієм ефективності (одному або декільком).

Основні принципи побудови математичної моделі динамічного програмування.

а) Необхідно порівнювати точність і дрібниці моделі, по-перше, з точністю тих вихідних даних, якими оперує дослідник, і по-друге, з тими результатами, які потрібно одержати.

б) Математична модель динамічного програмування повинна відбивати істотні риси досліджуваного явища й при цьому не повинна його сильно спрощувати.

в) Математична модель динамічного програмування не може бути повністю адекватна реальному явищу, тому для його дослідження краще використати декілька моделей, для побудови яких застосовані різні математичні методи. Якщо при цьому виходять подібні результати, то дослідження закінчується. Якщо результати сильно розрізняються, то варто переглянути постановку задачі.

г) Будь-яка складна система завжди піддається малим зовнішнім і внутрішнім впливам, отже, математична модель динамічного програмування повинна бути стійкої, тобто зберігати свої властивості й структуру при цих впливах.

На рисунку 1.4 зображена класифікація математичних моделей і місце динамічних моделей у загальній структурі (1).

По числу критеріїв ефективності математичні моделі діляться на однокритеріальні й багатокритеріальні. Багатокритеріальні математичні моделі містять два й більше критерії.

По обліку невідомих факторів математичні моделі діляться на детерміновані, стохастичні й моделі з елементами невизначеності.

У стохастичних моделях невідомі фактори – це випадкові величини, для яких відомі функції розподілу й різні статистичні характеристики (математичне очікування, дисперсія, середньоквадратичне відхилення й т.д.). Серед стохастичних можна виділити:

- моделі стохастичного програмування, у яких в цільову функцію (1.2) входять випадкові величини;

- моделі теорії випадкових процесів, призначені для вивчення процесів, стан яких у кожен момент часу є випадковою величиною;

- моделі теорії масового обслуговування, у якій вивчаються багатоканальні системи, зайняті обслуговуванням вимог. Також до стохастичних моделей можна віднести моделі теорії корисності, пошуку й прийняття рішень.

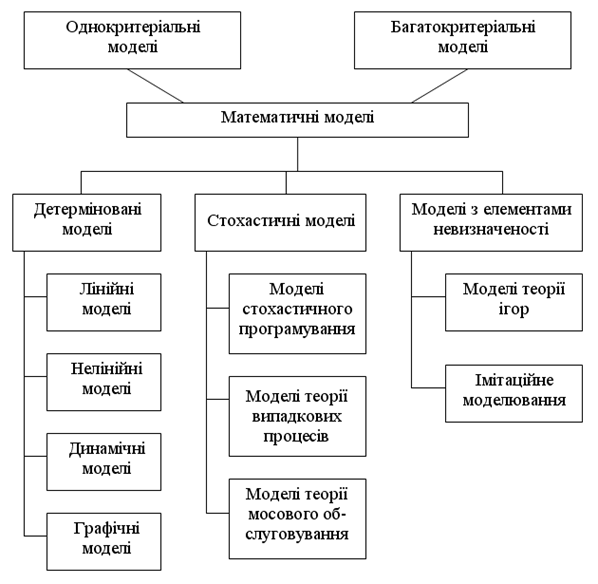
Рисунок 1.4 – Класифікація математичних моделей

Для моделювання ситуацій, що залежать від факторів, для яких неможливо зібрати статистичні дані й значення яких не визначені, використаються моделі з елементами невизначеності. У моделях теорії ігор задача представляється у вигляді гри, у якій беруть участь кілька гравців, що переслідують різні цілі, наприклад організацію підприємства в умовах конкуренції.

В імітаційних моделях реальний процес розвертається в машинному часі, і простежуються результати випадкових впливів на нього, наприклад організація виробничого процесу. У детермінованих моделях невідомі фактори не враховуються. Незважаючи на гадану простоту цих моделей, до них зводяться багато практичних задач, у тому числі більшість економічних задач. По виду цільової функції й обмежень детерміновані моделі діляться на лінійні, нелінійні, динамічні й графічні.

У лінійних моделях цільова функція й обмеження лінійні по керуючім змінним. Побудова й розрахунок лінійних моделей є найбільш розвиненим розділом математичного моделювання, тому часто до них намагаються звести й інші задачі або на етапі постановки, або в процесі рішення.

Нелінійні моделі – це моделі, у яких або цільова функція, або яке-небудь із обмежень (або всі обмеження) нелінійні по керуючим змінним. Для нелінійних моделей немає єдиного методу розрахунку. Залежно від виду нелінійності, властивостей функції й обмежень можна запропонувати різноманітні способи рішення. Однак, може трапитися й так, що для поставленої нелінійної задачі взагалі не існує методу розрахунку. У цьому випадку задачу варто спростити, або звести її до відомих лінійних моделей, або просто лінеаризувати модель.

У динамічних моделях на відміну від статичних лінійних і нелінійних моделей враховується фактор часу. Критерій оптимальності в динамічних моделях може бути самого загального виду (і навіть взагалі не бути функцією), однак для нього повинні виконуватися певні властивості. Розрахунок динамічних моделей складний, і для кожної конкретної задачі необхідно розробляти спеціальний алгоритм рішення (4).

Графічні моделі використаються тоді, коли завдання зручно представити у вигляді графічної структури.

2. ТЕОРЕТИЧНІ АСПЕКТИ ДИНАМІЧНОГО ПРОГРАМУВАННЯ

2.1 Постановка задачі динамічного програмування. Основні умови й область застосування

Динамічне програмування – це метод дослідження операцій, на кожному етапі якого можна керувати перебігом досліджуваного процесу та оцінювати якість такого управління.

Загальна постановка задачі динамічного програмування. Досліджується перебіг деякого керованого процесу, тобто на стан і розвиток якого можна впливати через певні проміжки (в економічних процесах управління – перерозподіл коштів, заміна обладнання, визначення обсягів поставок сировини на період і т. ін.). Приймається, що процес управління можна реалізувати дискретно за  етапів. Будь-яку багато етапну задачу можна реалізувати по-різному або відразу шукати всі елементи розв’язку для всіх етапів, або знаходити оптимальне управління поетапно, на будь-якому етапі визнаючи розв’язок стосовно лише цього етапу – такий варіант простіший.

Параметри цих моделей доцільно розбити на дві множини: параметри стану (для дослідження властивостей яких була розбудована модель) та параметри управління (фактори, які можуть впливати на стан процесу).

Нехай  – кількість етапів. На будь-якому і-му етапі процес може бути в різних станах {}, кожний з яких характеризується скінченою множиною параметрів. Множину параметрів доцільно розглядати як компоненти деякого вектора , де  – кількість параметрів, обраних для характеристики стану. На будь-якому з  досліджуваних етапів система може бути в кількох станах.

Перебіг процесу визначається певною послідовністю переходів з одного стану в інший. Якщо процес на і-му етапі перебував у деякому стані , то наступний стан  на (і+1)-му кроці визначається не лише попереднім станом, а й вибором певного управління при досягненні  (;). У загальному випадку будь-яке управління на будь-якому етапі доцільно розглядати як -мірний вектор . Числові значення компонент вектора управління будуть залежати як від вихідного стану  на і-му кроці, так і від наступного стану на (і+1)-му кроці , тобто вектор  визначається чотирма індексами  і має бути вибраний з певної множини допустимих управлінь.

Для спрощення записів вектори можливих поточного стану та управління будемо позначати лише одним індексом, спів ставляючи їх певному кроку (етапу), тобто щодо стану , мається на увазі один із можливих станів множини {}, а щодо вектора  – один із можливих векторів множини {}, ().

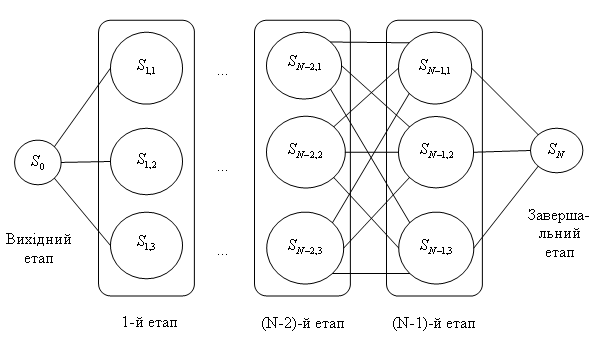
Рисунок 1.5 – Можливі стани системи на кожному етапі

На рисунку 1.5 схематично кругами зображені можливі стани на кожному етапі, лініями – можливі переходи від одного стану до іншого за вибору певного управління. Таким чином, стан процесу на і-му етапі визначається певною функціональною залежністю від стану на попередньому кроці та значеннями параметрів управління на початку чергового кроку, тобто . Процес управління моделюється як вибір за кожного можливого j-го стану на і-му етапі певного k-мірного вектора  з деяких допустимих множин векторів {}. Для спрощення він позначається . Множина послідовності управлінь позначається – , які переводять систему зі стану  у стан , схематично це представлено на рисунку 1.6.

Рисунок 1.6 – Перехід системи із стану  у стан

Будь-яку послідовність , що переводить систему зі стану  у стан , називається стратегією, а вектори  – її складовими.

Ефективність вибору послідовності управлінь  (стратегії) оцінюється за вибраним критерієм певною цільовою функцією :

.                                                                                             (2.1)

Модель динамічного програмування можна використовувати в тих випадках, коли є підстави прийняти такі допущення стосовно досліджуваної системи:

– Стан  системи в кінці і-го кроку визначається лише попереднім станом  та управлінням  на і-му кроці і не залежить від попередніх станів та управлінь. Формула (2.2) – рівняння стану.

, .                                                                         (2.2)

– Цільова функція (2.1) є адитивною стосовно кожного етапу і залежить від того, яким був стан системи  на початку етапу та яке було обране управління. Нехай  – показник ефективності і-го кроку.

, .                                                                         (2.3)

Тоді цільова функція (2.1) буде представлена формулою (2.4)

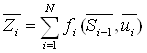.                                                                                   (2.4)

Метод динамічного програмування також можна використовувати при розв’язанні задач з так званою “мультиплікативною” цільовою функцією, тобто:

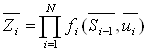.                                                                                   (2.5)

Задача динамічного програмування за названих умов формується так: визна