Скачать

Моделирование электростатического поля

Матвеев Виктор Михайлович, Вольф Александр

Электростатическое поле характеризуется в каждой точке пространства значением вектора напряженности E и значением электростатического потенциала. Направление вектора напряженности в каждой точке поля и распределение потенциала в поле можно сделать наглядным, если провести линии напряженности и поверхности равного потенциала.

Часто изучение электростатического поля между системой заряженных проводников заменяют изучением поля электрического тока между той же системой проводников, если потенциалы проводников поддерживают постоянными и проводимость среды много меньше проводимости проводников. Такой способ изучения электростатического поля путем создания другого, эквивалентного ему поля называют моделированием электростатического поля.

Метод моделирования электростатического поля имеет широкое применение на практике. Пользуясь этим методом, изучают сложные электростатические поля (в электростатических линзах, в электронных трубках и т.п.). При этом широко пользуются методом подобия, которое утверждает, что если размеры электродов, создающих поле, и все расстояния между этими электродами изменить в одной пропорции, то структура поля останется прежней.

Экспериментально легче вести измерения потенциалов электростатического поля, т.к. большинство электроизмерительных приборов измеряют разности потенциалов между различными точками. Обычно экспериментально изучается распределение потенциалов в поле, проводятся поверхности равного потенциала (эквипотенциальные поверхности), а линии напряженности строятся как ортогональные линии к эквипотенциальным поверхностям.

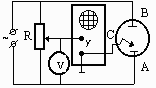Экспериментальная установка представлена на рис. 1. Перемещая щуп (С), от одного электрода (А) к другому (В) выбирают такое его положение, при котором разность потенциалов на вертикально отклоняющих пластинах равна нулю. При этом на экране широкая полоса стягивается в линию, а вольтметр показывает потенциал эквипотенциальной линии относительно электрода (А). Точка, в которой находится щуп является точкой эквипотенциальной поверхности. С перемещением движка реостата изменяется величина потенциала.

В качестве дополнения к данной работе разработана программа FIELD. Она предназначена для компьютерного моделирования электрических полей системы точечных зарядов. Таким образом, появляется возможность экспериментально определить линии напряженности и эквипотенциальные поверхности и тут же смоделировать аналогичную ситуацию на компьютере.

По принципу суперпозиции полей напряженность E(r) в точке r, обусловленная системой точечных зарядов q₁, q₂, q₃, ..., q_N равна

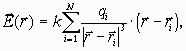 (1)

где r_i - координата неподвижного i- го заряда и k - постоянная, которая зависит от системы единиц.

Наглядно векторное поле удобно изображать в виде силовых линий. Алгоритм вычерчивания силовых линий в двухмерном случае выглядит следующим образом:

1. Выбираем точку (x, y) и вычисляем компоненты E_x и E_y вектора электрического поля E по формуле (1).

2. Проводим в этой точке небольшой прямолинейный отрезок заданной длины в направлении E. Компоненты этого отрезка равны

и (2)

3. Повторяем данную процедуру с новой точки (). Продолжаем до тех пор, пока силовая линия не уйдет в бесконечность или не подойдет к какому-нибудь отрицательному заряду.

Часто легче исследовать свойства системы, рассматривая энергетические характеристики, а не силовые. Энергетической характеристикой электрического поля является потенциал (), определяемый для точечного заряда соотношением. Между напряженностью поля и потенциалом существует следующее соотношение

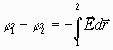или. (3)

Так как силовые линии электрического поля ортогональны эквипотенциальным поверхностям, то этим свойством можно воспользоваться, чтобы с помощью программы FIELD нарисовать последние. Поскольку компоненты вектора прямолинейного отрезка определяются формулами (2), то компоненты отрезка, перпендикулярного E, а значит, параллельного эквипотенциальной поверхности, равны

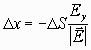и (4)

Неважно какой знак присвоить компонентам x и y, поскольку это скажется лишь на направлении рисования.

Для подготовки данной работы были использованы материалы с сайта http://www.physfac.bspu.secna.ru/