Минимизация функций нескольких переменных. Метод спуска
Метод оптимизации как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.
Необходимость принятия наилучших решений так же стара, как само человечество. Испокон веку люди, приступая к осуществлению своих мероприятий, раздумывали над их возможными последствиями и принимали решения, выбирая тем или другим образом зависящие от них параметры - способы организации мероприятий. Но до поры, до времени решения могли приниматься без специального математического анализа, просто на основе опыта и здравого смысла.
Возьмем пример: человек вышел утром из дому, чтобы ехать на работу. По ходу дела ему приходится принять целый ряд решений: брать ли с собой зонтик? В каком месте перейти улицу? Каким видом транспорта воспользоваться? И так далее. Разумеется, все эти решения человек принимает без специальных расчетов, просто опираясь на имеющийся у него опыт и на здравый смысл. Для обоснования таких решений никакая наука не нужна, да вряд ли понадобится и в дальнейшем.
Однако возьмем другой пример. Допусти, организуется работа городского транспорта. В нашем распоряжении имеется какое-то количество транспортных средств. Необходимо принять ряд решений, например: какое количество и каких транспортных средств направить по тому или другому маршруту? Как изменять частоту следования машин в зависимости от времени суток? Где поместить остановки? И так далее.
Эти решения являются гораздо более ответственными, чем решения предыдущего примера. В силу сложности явления последствия каждого из них не столь ясны; для того, чтобы представить себе эти последствия, нужно провести расчеты. А главное, от этих решений гораздо больше зависит. В первом примере неправильный выбор решения затронет интересы одного человека; во втором - может отразиться на деловой жизни целого города.
Наиболее сложно обстоит дело с принятием решений, когда речь идет о мероприятиях, опыта, в проведении которых еще не существует и, следовательно, здравому смыслу не на что опереться, а интуиция может обмануть. Пусть, например, составляется перспективный план развития вооружения на несколько лет вперед. Образцы вооружения, о которых может идти речь, еще не существуют, никакого опыта их применения нет. При планировании приходится опираться на большое количество данных, относящихся не столько к прошлому опыту, сколько к предвидимому будущему. Выбранное решение должно по возможности гарантировать нас от ошибок, связанных с неточным прогнозированием, и быть достаточно эффективным для широкого круга условий. Для обоснования такого решения приводится в действие сложная система математических расчетов.
Вообще, чем сложнее организуемое мероприятие, чем больше вкладывается в него материальных средств, чем шире спектр его возможных последствий, тем менее допустимы так называемые "волевые" решения, не опирающиеся на научный расчет, и тем большее значение получает совокупность научных методов, позволяющих заранее оценить последствия каждого решения, заранее отбросить недопустимые варианты и рекомендовать те, которые представляются наиболее удачными.
Методы спуска
Общая схема
Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. Это позволяет написать общую схему методов спуска.
Решается задача минимизации функции j(x) на всём пространстве En. Методы спуска состоят в следующей процедуре построения последовательности {xk}. В качестве начального приближения выбирается любая точка x0ÎEn. Последовательные приближения x1, x2, … строятся по следующей схеме:
1) в точке xk выбирают направление спуска - Sk;
2) находят (k+1)-е приближение по формуле xk+1=xk-hkSk.
Направление Sk выбирают таким образом, чтобы обеспечить неравенство f(xk+1) Число hk определяет расстояние от точки xk до точки хk+1. Это число называется длиной шага или просто шагом. Основная задача при выборе величины hk - это обеспечить выполнение неравенства j(xk+1) Величина шага сильно влияет на эффективность метода. Большей эффективностью обладает вариант метода, когда шаг по каждой переменной определяется направляющими косинусами градиента(в градиентных методах). xk+1=xk-hk cos где - cos В этом случаи величина рабочего шага не зависит от величины модуля градиента, и ею легче управлять изменением h . В районе оптимума может возникать значительное «рыскание», поэтому используют различные алгоритмы коррекции h. Наибольшее распространение получили следующие алгоритмы: 1. 2. 3. где (например, Вдали от оптимума направление градиента меняется мало, поэтому шаг можно увеличить (второе выражение), вблизи от оптимума направление резко меняется (угол между градиентами R(x) большой), поэтому h сокращается (третье выражение). Метод покоординатного спуска Пусть нужно найти наименьшее значение целевой функции u=f(M)=f(x, x, . . . ,xn). Здесь через М обозначена точка n-мерного пространства с координатами x, x, . . . ,xn: M=(x, x, . . . ,xn). Выберем какую-нибудь начальную точку М=(x, x, . . . ,xn0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x, x,x, . . . ,xn0 ). Тогда она превратится в функцию одной переменной x . Изменяя эту переменную, будем двигаться от начальной точки x=x в сторону убывания функции, пока не дойдем до ее минимума при x=x, после которого она начинает возрастать. Точку с координатами ( x, x,x, . . . ,xn0) обозначим через М, при этом f(M0) f(M). Фиксируем теперь переменные: x=x, x= x, . . . ,xn=xn0 и рассмотрим функцию f как функцию одной переменной x: f(x, x, x . . . ,xn0). Изменяя x , будем опять двигаться от начального значения x2=x20 в сторону убывания функции, пока не дойдем до минимума при x2=x21 .Точку с координатами {x, x, x . . . xn0} обозначим через М, при этом f(M1) f(M). Проведем такую же минимизацию целевой функции по переменным x, x, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек МММ. . . , которой соответствует монотонная последовательность значений функции f(M0) f (M)f(M)Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области. Проведем такую же минимизацию целевой функции по переменным x, x, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М,М,М, . . . , которой соответствует монотонная последовательность значений функции f(M0)f(M)f(M) Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области. Отметим , что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция f(x, x, ... ,xn) задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов На рис.изображены линии уровня некоторой функции двух переменных u= f (х, у). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода. Пусть требуется решить задачу (2): f(x) В двумерном пространстве R2. Решение задачи (2) методом покоординатного спуска, иначе называемого методом Гаусса - Зейделя, производят по следующей общей схеме. Выбирают произвольно начальную точку х(0) из области определения функции f(х). Приближения х(k) определяются соотношениями (3): x(k+1)=x(k)+t(k)S(k) (k=0,1,2, ...), где вектор направления спуска s(k)- это единичный вектор, совпадающий с каким-либо координатным направлением (например, если S(k) параллелен х1, то S(k)= {1,0,0,...,0}, если он параллелен x2, то S(k)={0, 1, 0, . . . ,0} и т.д.) ; величина t(k) является решением задачи одномерной минимизации: f(x(k)+ts(k)) Блок-схема поиска минимума функции двух переменных методом покоординатного спуска. дискретный оптимизация спуск функция Метод градиентного спуска Рассмотрим функцию f, считая для определенности, что она зависит от трех переменных x,y,z. Вычислим ее частные производные дf/дх, дf/ду, дf/дz и образуем с их помощью вектор, который называют градиентом функции: grad f(x, у, z) = дf (х, у,z) /дх*i+дf( x, у, z)/ду*j+дf(x, y,z)/дг*k. Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции f по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (х, у,z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента grad (х, у,z)дf/дх (х, у,z))2 +(дf/ду( x, у, z))2+(дf/дг(x, y,z))2. определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (х, у, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных. Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом. Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска. Метод градиентного спуска требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно. Отметим, что при таких расчетах gi ,нельзя брать слишком малым, а значения функции нужно вычислять с достаточно высокой степенью точности, иначе при вычислении разности f(x1, ...,xi+ gi, ..., xn) - f(x1, ..., xi, ..., xn) f(x1, ...,xi+ gi, ..., xn) - f(x1, ..., xi- gi,..., xn) будет допущена большая ошибка. Первый алгоритм требует меньших затрат по сравнению со вторым (обычно затраты выражаются количеством вычислений критерия оптимальности), но позволяет получить решение менее точно, чем второй, эта погрешность зависит от величины пробного шага Метод наискорейшего спуска Суть метода наискорейшего спуска состоит в следующем. Как и прежде, в начальной точке определяется антиградиент минимизируемой функции. Однако теперь в направлении антиградиента делается ни один шаг, а движутся в данном направлении до тех пор, пока целевая функция убывает, достигает в некоторой точке минимума. В этой точке опять определяют антиградиент и ищут новую точку минимума целевой функции и так далее. В данном методе спуск имеет более целеустремлённый характер, производится более крупными шагами и градиент функции вычисляется в меньшем числе точек. Описание программы: Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по схеме Вычисление градиента происходит по методу с парными пробами, это улучшает поиск за счёт более точного вычисления градиента. Метод наискорейшего спуска по сравнению с обычным градиентным методом дает некоторое ускорение , метод хорошо "работает" при минимизации гладких функций и если начальное приближение выбрано достаточно далеко от оптимума. Если же очередная точка окажется в окрестности оптимума, то уменьшение целевой функции будет очень медленным. Это происходит из-за того, что для получения оптимума с высокой точностью необходимо выполнить большое число мелких шагов. Метод наискорейшего спуска хотя не дает особенного ускорения сходимости он свободен от параметров и на практике может дать некоторый выигрыш, особенно на начальных итерациях. В связи с этим в программе был реализован более точный метод градиентного спуска. В качестве условия окончания поиска задаётся требуемая малость модуля градиента функции, т.е. должно выполнятся условие (В области оптимума градиент равен 0, но достичь этого значения практически не возможно, поэтому задаётся требуемая малость близкая к 0). Так же в программе можно задавать номер итерации выхода из цикла, Другими словами при достижении какого количества точек прерывать цикл, если он не прервется сам раньше. h=0,1; x1 =-0,5; x2=-1 ; x1нач=-2, x1кон=2, x2нач=-2, x2кон=2 h=0,2; x1 =-0,5; x2=-1 ; x1нач=-2, x1кон=2, x2нач=-2, x2кон=2 h=0,3; x1 =-0,5; x2=-1 ; x1нач=-2, x1кон=2, x2нач=-2, x2кон=2 h=1; x1 =-0,5; x2=-1 ; x1нач=-2, x1кон=2, x2нач=-2, x2кон=2 Самарский государственный аэрокосмический университет имени академика С.П.Королева Кафедра высшей математикиРасчетно-пояснительная Линейное программирование наука о методах исследования и отыскания экстремальных значений линейной функции, на параметры которой нал ПОХІДНІ ТА ДИФЕРЕНЦІАЛИ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ1 Частинні похідніНехай функція визначена в деякому околі точки . Надамо змінній x п Расчетно-графическая работапо теории алгоритмовНа тему«Решение задачи коммивояжера методом ветвей и границ»План1. Вступление2. Поста В 1931 г. В одном из немецких научных журналов появилась сравнительно небольшая статья с довольно устрашающим названием «О формально нер ФУНКЦІЯ, ЇЇ ГРАНИЦЯ ТА НЕПЕРЕРВНІСТЬ1. Функція багатьох змінних. Означення та символікаНехай задано множину упорядкованих пар чисел. Copyright © https://www.referat-web.com/. All Rights Reserved![]()
![]() =
=![]()
![]() (без коррекции);
(без коррекции);![]() если
если ![]() ;
; ![]() если
если ![]()
![]() , если
, если ![]() ;
; ![]() , если
, если![]() ;
; ![]() ,если
,если ![]() ,
,![]() –угол между градиентами на предыдущем и текущем шаге;
–угол между градиентами на предыдущем и текущем шаге;![]() и
и![]() – заданные пороговые значения выбираются субъективно
– заданные пороговые значения выбираются субъективно![]() ).
).![]() min, х Rn. (2)
min, х Rn. (2)![]() min, t R1, (k=0,1,2, ...), и может определяться, в частности, методом сканирования. Детальная реализация общей схемы в двумерном случае R2 дает траекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), x1(k) x(k+1) (k=0, 1, 2,) . При k=0, исходя из начальной точки х(0)=(x1(0),x2(0)), находят точку х(0)= (x1(0),x2(0)), минимума функции одной переменной f(x1,x2(0)); при этом f(x(0))f(x(0)).Затем находят точку минимума x(1) функции f (x1(0),x2) по второй координате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируя вторую координату точки х(1), находят точку минимума х(1)= (x1(1),x2(1)), функции f(x1,x2(1)) одной переменной x(1); при этом f(x(1))f(x(1))f(x(0)). Точку х(2) получают, минимизируя целевую функцию f(x1(1),x2), вновь по коорданате х2, фиксируя координату x1(1) ,точки x(1) , и т.д. Условием прекращения вычислительной процедуры при достижении заданной точности может служить неравенство x(k+1) - x(k) <
min, t R1, (k=0,1,2, ...), и может определяться, в частности, методом сканирования. Детальная реализация общей схемы в двумерном случае R2 дает траекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), x1(k) x(k+1) (k=0, 1, 2,) . При k=0, исходя из начальной точки х(0)=(x1(0),x2(0)), находят точку х(0)= (x1(0),x2(0)), минимума функции одной переменной f(x1,x2(0)); при этом f(x(0))f(x(0)).Затем находят точку минимума x(1) функции f (x1(0),x2) по второй координате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируя вторую координату точки х(1), находят точку минимума х(1)= (x1(1),x2(1)), функции f(x1,x2(1)) одной переменной x(1); при этом f(x(1))f(x(1))f(x(0)). Точку х(2) получают, минимизируя целевую функцию f(x1(1),x2), вновь по коорданате х2, фиксируя координату x1(1) ,точки x(1) , и т.д. Условием прекращения вычислительной процедуры при достижении заданной точности может служить неравенство x(k+1) - x(k) < 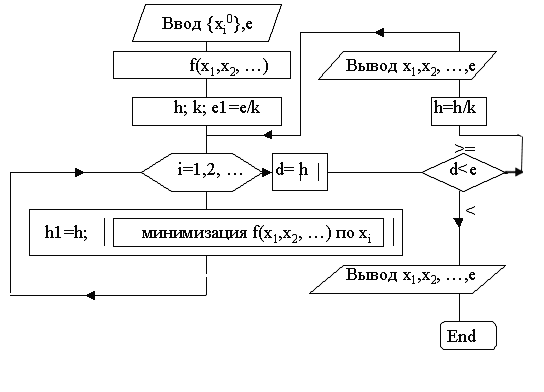
![]() если
если ![]() ;
; ![]() если
если ![]()
![]()
Исследование функции
U=1*x1^3+2*x2^2-3*x1-4*x2
(изменением шага).
№ x1 x2 R 0 -0,5 -1 7,375 1 -0,2750 -0,1999 1,6842 2 0,0023 0,2800 -0,9701 3 0,3023 0,5680 -2,5059 4 0,5749 0,7408 -3,4002 5 0,7757 0,8445 -3,8120 6 0,8952 0,9067 -3,9508 7 0,9548 0,9440 -3,9877 8 0,9813 0,9664 -3,9967 9 0,9924 0,9798 -3,9990 10 0,9969 0,9879 -3,9997 11 0,9988 0,9927 -3,9999 12 0,9995 0,9956 -4,0000 13 0,9998 0,9974 -4,0000 14 1,0000 0,9984 -4,0000 № x1 x2 R 0 -0,5 -1 7,375 1 0,0500 0,6000 -1,5301 2 0,5485 0,9200 -3,4676 3 0,9680 0,9840 -3,9964 4 1,0058 0,9968 -3,9999 5 0,9988 0,9994 -4,0000 № x1 x2 R
0 -0,5 -1 7,375 1 0,1750 1,4 -2,1996 2 1,0473 0,9200 -3,9804 3 0,9600 1,016 -3,9948 4 1,0305 0,9968 -3,9972 5 0,9747 0,0006 -3,9981 6 1,0196 0,9999 -3,9988 7 0,9839 1,0000 -3,9992 8 1,0126 1,0000 -3,9995 9 0,9898 1,0000 -3,9997 10 1,0081 1,0000 -39998 11 0,9935 1,0000 -3,9999 12 1,0052 1,0000 -3,9999 13 0,9958 1.0000 -3,9999 14 1,0033 1,0000 -4,0000 15 0,9973 1,0000 -4,0000 16 1,0021 1,0000 -4,0000 17 0,9983 1,0000 -4,0000 18 1,0013 1,0000 -4,0000 № x1 x2 R 0 -0,5 -1 7,375 1 0,6250 3 4,3692 2 1,5391 -1,0000 5,0283 3 0,5125 1 -3,4029 4 1,0655 Подобное:
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

