Скачать

Методы оценки температурного состояния

Содержание

1. Методы оценки температурного состояния

2. Постановка нестационарной краевой задачи теплопроводности в

системе, включающей прошивную оправку

2.1 Условия однозначности или краевые условия задачи

2.2 Математическая формулировка задачи расчета температурного поля оправки

3. Метод и алгоритм решения уравнений теплообмена

4. Методы оценки термонапряженного состояния

4.1 Физические основы возникновения термических напряжений

4.2 Формулировка задач термоупругости

5. Расчет температурных полей и полей напряжений в оправке при циклическом режиме работы

6. Износостойкость прошивных оправок

7. Основные выводы из полученных результатов

Список использованных источников

1. Методы оценки температурного состояния

На начальном этапе объектом исследования является тепловое поле, перенос тепла в системе тел. Тепловое поле на данный момент времени t определяется распределением температуры по телу, т.е. функцией , где ) - декартовы координаты. Передача тепла может осуществляться теплопроводностью, конвекцией или излучением. В рассматриваемой задаче происходит сложный теплообмен, т.е. передача тепла осуществляется различными способами. Необратимый процесс теплопроводности описывается феноменологическим законом Фурье.

Температурное поле может быть стационарным, в этом случае температура во всех точках тела не зависит от времени, и нестационарным. Если температура изменяется только по одной пространственной координате, то температурное поле одномерное. Если по двум координатам - двухмерное.

Для оценки температурного состояния прошивной оправки в процессе прошивки, то есть для математического определения температурного поля, необходимо решить дифференциальные уравнения теплового состояния (уравнения теплопроводности). Принимается допущение, что температурное поле прошивной оправки является осесимметричным. Рассматривается двумерная задача теплопроводности (все величины зависят от двух координат).

При решении задач теплопроводности составляют сеточные уравнения. Методы решения сеточных уравнений в задачах теплопроводности делятся на прямые (метод Гаусса, метод квадратного корня или метод Холецкого, метод алгебраической прогонки, метод редукции, метод разделения переменных), итерационные (двухслойный итерационный метод, диагональный оператор B, треугольный итерационный метод и др.) и численные.

Приближенное решение задачи теплопроводности осуществляется численными методами (сеточными и проекционными). Сеточные (разностные) методы основаны на переходе от функций непрерывного аргумента к функциям дискретного аргумента. В проекционных методах функции непрерывного аргумента приближаются также функциями непрерывного аргумента. Также существуют и значительно распространены проекционно-сеточные методы (метод конечных элементов). Этот класс методов определяется специальным выбором элементов (конечных элементов).

Сеточные методы являются наиболее универсальным способом решения линейных задач в областях сложной формы, которые не всегда можно решить классическим способом. При решении составляется семейство разностных задач, которое ставится в соответствие непрерывной задаче. Это семейство называют разностной схемой. Разностные схемы применяются как для стационарных, так и для нестационарных задач, но в случаях стационарной и нестационарной теплопередач имеются некоторые различия в разностных схемах. Задача состоит в получении приближенного решения с некоторой заданной точностью. Это достигается на пути перехода от непрерывной задачи к дискретной. При построении дискретной задачи, т.е. при аппроксимации уравнений и граничных условий требуется сохранить за разностным решением характеристики искомого решения. Примером является свойство консервативности - выполнение законов сохранения и для разностной задачи. Консервативные схемы - это разностные схемы, выполняющие законы сохранения на сетке. В отличие от консервативных схем, неконсервативные схемы расходятся в случае разрывного коэффициента теплопроводности. Вторым примером служит свойство монотонности - выполнение принципа максимума и минимума разностного решения. Разностное решение должно сходиться к точному при измельчении сетки.

Консервативная разностная схема строится в одномерном или двумерном случае. Конечно элементная схема строится в двумерном плоском случае.

Далее рассматриваются способы построения разностных схем при решении задач теплопроводности численными методами.

Разностные схемы для задачи стационарной теплопроводности.

В случае стационарного температурного поля перенос тепла осуществляется теплопроводностью, а температура описывается эллиптическим уравнением второго порядка с определенными краевыми условиями.

Для применения разностных методов в области изменения переменных G вводят сетку. Все производные и краевые условия заменяют разностями значений функции в узлах сетки. При написании каждого разностного уравнения около некоторого узла сетки берется одно и то же количество узлов, образующее строго определенную конфигурацию. Эта конфигурация узлов, которые используются для построения разностного оператора, называется шаблоном разностной схемы. Узлы, в которых разностная схема записана на шаблоне, называются регулярными, а все остальные узлы - нерегулярными. На рис.1.1 показан пример прямоугольной равномерной сетки. Здесь:  - переменные.

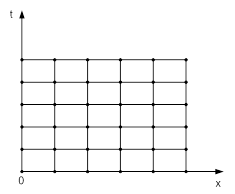
Рис.1.1 Пример прямоугольной равномерной сетки, построенной для прямоугольной области изменения переменных G (x,t).

Для нерегулярных областей в ряде случаев удается построить согласованную сетку, которая образована узлами обычной прямоугольной неравномерной сетки с узлами, лежащими на границе (эти узлы согласованы). Пример согласованной разностной сетки для нерегулярной области приведен на рис.1.2

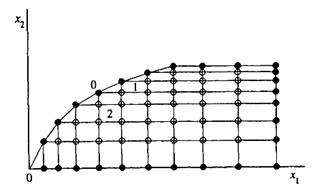
Рис.1.2 Пример нерегулярной согласованной разностной сетки.

Исходная дифференциальная задача при аппроксимации заменяется сеточной. Соответствующие разностные (сеточные) уравнения есть система линейных алгебраических уравнений для неизвестных значений сеточной функции.

Другой способ построения разностных схем основан на методе конечных элементов.

Разностная схема метода конечных элементов.

Построение разностных схем может осуществляться на основе метода конечных элементов. Для построения конечномерного подпространства исходная расчетная область разбивается на некоторые элементарные ячейки. В двумерном случае в качестве таковых наиболее подходящими являются треугольники, причем внутри таких ячеек приближенное решение является линейной функцией. Такого вида сетки выбраны в связи с возможностью решения задач в областях достаточно произвольной формы. На рис.1.3 показана равномерная сетка с шагом .

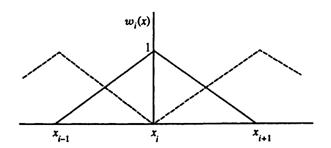
Рис.1.3 Равномерная конечноэлементная сетка, состоящая из треугольников, применяемая в методе конечных элементов.

В рассматриваемой области фиксируется конечное число точек, которые называют узлами (узловыми точками). Непрерывная величина аппроксимируется моделью, состоящей из отдельных элементов. На каждом из этих элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией. Выбираются аппроксимирующие базисные функции  в виде кусочных полиномов малой степени или полиномов более высоких степеней (квадратичных, кубических и др.) Полином, связанный с данным элементом называют функцией элемента. Далее строится разностная схема.

Разностные схемы для нестационарных задач.

Нестационарные тепловые поля описываются параболическими уравнениями второго порядка. Разностные схемы составляются многослойными. Например, при использовании двухслойной разностной схемы в разностное уравнение входят значения на двух временных слоях.

Для нестационарных задач в области вводится пространственная сетка, с которой связывается некоторое конечномерное пространство. Вводится сетка и по времени, для простоты, равномерная. Приближенное решение рассматривается как функция дискретного аргумента. Операторно-разностная схема связывает разностное решение на нескольких временных слоях. Такая разностная схема является многослойной.

У данной задачи есть и начальные, и граничные условия, поэтому задача является нестационарной (смешанной) краевой. Задача имеет нелинейный характер, т.е. теплофизические свойства среды зависят от температуры и граничные условия нелинейны.

Метод конечных разностей.

В качестве метода решения системы дифференциальных уравнений выбирается численный математический метод конечных разностей - широко известный и простейший метод интерполяции. Метод конечных разностей означает по сути обратный переход от дифференциальной модели к интегральной. При осуществлении данной методики строится конечно-разностная сетка и записываются конечно-разностные аналоги дифференциальных уравнений теплопроводности (разностная схема). Для аппроксимации дифференциальных уравнений теплопроводности применяется неявная консервативная итерационная разностная схема, реализуемая градиентным методом покоординатного спуска (Гаусса-Зейделя), являющимся классическим итерационным методом решения системы линейных уравнений. Неявной она является потому, что содержит несколько неизвестных значений функции на новом слое. Это означает, что значение функции нельзя явно выразить через значения функции на данном слое. Такая схема является безусловно устойчивой. Неявность разностной схемы достигается применением итерационной процедуры на каждом временном слое. Решение в узлах сетки получается приближенным (разностным). Поскольку одна из переменных имеет физический смысл времени t, то сетка строится так, чтобы среди ее линий были линии t=t_m, где m - номер индекса дискретного момента времени. То есть переменная t не непрерывна, а увеличивается на дискретное значение. Решение численной задачи получается в виде таблицы.

Экономичные разностные схемы нестационарной теплопроводности.

Поскольку при использовании неявных схем вычислительные затраты высоки, применяют методы реализации разностных схем, которые по вычислительной реализации были бы аналогичны явным схемам. К таким методам относятся явный итерационный метод, метод переменных направлений, попеременно-треугольный метод, итерационный метод с эллиптическим оператором B. Для явных схем число арифметических операций, приходящихся на один узел сетки не зависит от общего числа узлов. Разностные схемы метода переменных направлений основываются на представлении оператора по пространственным переменным в виде суммы операторов, каждый из которых является одномерным (1), (2).

Постановка нестационарной краевой задачи теплопроводности начинается с задания краевых условий и выбора систем координат. Далее рассматривается методика составления краевых условий данной задачи.

2. Постановка нестационарной краевой задачи теплопроводности в

системе, включающей прошивную оправку

2.1 Условия однозначности или краевые условия задачи

Геометрические условия.

Оправка - это сплошное тело сложной формы (при решении задачи термоупругости не рассматривается возможное наличие в оправке специальных каналов для подачи охлаждающей жидкости, хотя они часто применяются на практике). Диаметр оправки зависит от внутреннего диаметра гильзы. Оправка подразделяется на участки различной геометрической формы: сферическую часть, коническую часть до пережима, коническую часть после пережима и часть штока, примыкающую к оправке. Длины этих участков рассчитываются по известным формулам.

Постановка краевой задачи зависит от выбора системы координат. Простейший подход к решению задач в нерегулярных областях состоит в использовании криволинейных координат, в которых расчетная область становится регулярной (понятия регулярной и нерегулярной областей были рассмотрены в разделе 1). Для сферического участка I принята сферическая система координат. Для участков II, III, IV принята цилиндрическая система координат.

Диаметр оправки на третьем участке равен:

,(2.1)

где  - внутренний диаметр гильзы. Диаметр полусферы равен:

. (2.2)

Длина первого участка:

. (2.3)

Длина второго участка:

,(2.4)

где  - конусность конической части оправки ().

Длина третьего участка:

. (2.5)

Площадь поперечного сечения гильзы на выходе при заданных внутреннем диаметре гильзы и толщине стенки трубы рассчитывается по формуле:

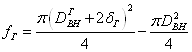. (2.6)

Площадь поперечного сечения металла в зазоре валок - оправка определяется как:

,(2.7)

где  и  - текущее значение радиуса валка и радиуса оправки, вычисляемое по следующим тригонометрическим соотношениям:

для сферической части оправки

; (2.8)

для конической части оправки до пережима

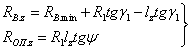; (2.9)

для конической части оправки после пережима

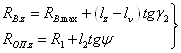,(2.10)

где  - радиус валка в сечении носка оправки;  - радиус сферической части оправки;  - угол от оси сферы до расчетного сечения сферической части оправки;  - угол входного конуса валка (3°...4°);  - угол выходного конуса валка (3°30'...6°);  - угол конусности оправки;  - текущая длина второго участка оправки;  - выдвижение оправки за пережим.

На поверхности оправки образуется слой окалины. Толщина окалинообразующего слоя на поверхности оправки .

Физические условия.

При прошивке происходит теплообмен в системе тел: валки - линейки - гильза - слой окалины - оправка. Температура валков и линеек принимается постоянной. Источниками тепла являются нагретая заготовка и внутренние источники (деформационный разогрев, разогрев за счет сил трения). Тепловая энергия в процессе прошивки поступают на разогрев технологического инструмента. В период между прошивками оправка охлаждается на воздухе или в проточной воде.

Прошивная оправка является сплошным однородным изотропным телом. Ее теплопроводность является скалярной величиной. В качестве материала оправки выбирается сталь марки 30Х2МФА и 38ХНЗМФА. Физическими параметрами оправки являются плотность , удельная массовая теплоемкость оправки , коэффициент теплопроводности материала оправки . Внутренние источники тепла в оправке отсутствуют.

Время нагрева оправки при прошивке определяется по скорости движения металла  и заданной длине гильзы :

. (2.11)

Условия на границе металл - оправка.

Теплофизическими свойствами металла являются плотность , удельная массовая теплоемкость металла , коэффициент теплопроводности металла . При деформации металла происходит выделение теплоты.

Для определения кондуктивного и лучистого тепловых потоков на границе контакта металл - оправка необходимо предварительно рассчитать температуру металла в зазоре между валками, линейками и прошивной оправкой. Эта температура деформируемого металла в процессе прошивки зависит, с одной стороны, от тепловыделений за счет работы сил трения и при формоизменении металла, а с другой стороны, от теплоотдачи к оправке, валкам, линейкам и окружающей среде. В общем случае среднюю температуру металла за время одной прошивки можно рассчитать по формуле:

,(2.12)

где  - средняя температура металла на входе в прошивной стан, рассчитывается по известному температурному полю заготовки перед прошивкой:

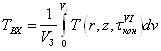,(2.13)

где  - объем заготовки;  - время охлаждения заготовки на воздухе перед станом;  - среднее повышение температуры металла при прошивке, которое определяется из уравнения теплового баланса очага деформации:

,(2.14)

где:  - удельная объемная теплоемкость металла;  - объем очага деформации;  - общее количество энергии, затраченной на процесс деформирования;  - коэффициент выхода теплоты;  - теплота, поступающая в металл за счет работы сил трения;  - тепловые потери очага деформации в окружающую среду и технологический инструмент;  - поправочный коэффициент, полученный экспериментально.

Общее количество энергии на деформацию определяется по теоретической формуле П.И. Полухина:

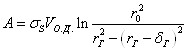,(2.15)

где  и  - радиус заготовки до прошивки и радиус гильзы;  - толщина стенки гильзы;  - сопротивление металла деформированию, рассчитывается по эмпирической формуле

,(2.16)

 - сопротивление деформации, выбираемое по величине среднего единичного обжатия;  - обжатие в пережиме.

Теплота, поступающая в металл при трении, рассчитывается по формуле:

,(2.17)

в которой  - коэффициент, учитывающий долю теплоты, поступающей на оправку от трения;  - плотность теплового потока за счет работы сил трения;  - коэффициент контакта;  - площадь поверхности металла под оправкой;  - время прошивки.

Тепловые потери металла в очаге деформации за время прошивки составляют величину:

,(2.18)

где ,  и  - площади поверхностей контакта металла с валками, линейками и окружающей средой; , , ,  - плотности тепловых потоков;  - плотность потока тепловых потерь в окружающую среду;  и  - плотности потоков тепловых потерь к валкам и линейкам рассчитываются при допущении квазистационарного режима теплопроводности с учетом температурного сопротивления слоя окалины:

,(2.19)

где  и  - температура валков и линеек в стационарном режиме работы.

Кондуктивный теплообмен между металлом и оправкой через слой окалины в месте контакта или через воздушный зазор, в первом приближении, рассчитывается при допущении квазистационарного режима теплообмена.

Через слой окалины:

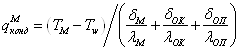; (2.20)

через воздушный зазор:

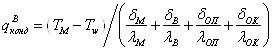,(2.21)

где  - средняя температура металла при прошивке;  - температура поверхности оправки; ,  - толщина приграничного слоя металла и оправки; ,  - толщина окалины и воздушной прослойки; , , ,  - коэффициенты теплопроводности деформируемого металла, оправки, окалины и воздуха соответственно.

Плотность лучистого теплового потока в воздушном зазоре находится при допущении равенства поверхностей, расположенных по обе стороны зазора. Учитывая, что воздух является диатермичной средой, получим

,(2.22)

где  - постоянная Стефана - Больцмана;  - приведенная степень черноты. Плотность теплового потока, выделяемого при работе сил трения, определяется по формуле:

,(2.23)

где  - касательное напряжение трения;  - скорость перемещения металла вдоль оси оправки (оси Oz).

Касательное напряжение трения рассчитывается по формуле

,(2.24)

в которой  - коэффициент трения; Р - сила нормального давления на оправку.

Для конических оправок различных геометрических размеров значения давлений, сохраняются на носке, в конце сферической части, в пережиме и в конце третьего участка.

Скорость течения металла в рассматриваемом расчетном сечении находится из уравнения неразрывности, которое при некотором допущении имеет вид:

,(2.25)

где  - средняя скорость перемещения металла в сечении  между валком и оправкой;  - скорость движения гильзы на выходе из зазора. Скорость выхода гильзы определена экспериментально в зависимости от угла подачи .

Величина деформационного разогрева  зависит не только от величины внутренних тепловыделений при деформации, но и от интенсивности теплообмена с окружающей средой и технологическим инструментом, поэтому для ее определения необходимо применить метод итераций. В качестве первого приближения  рассчитывается при допущении равенства нулю тепловых потоков  и .

Условия на границе металл - окалина.

Окалинообразующий слой очень существенно влияет на температурное поле оправки. Теплофизические свойства окалины характеризуются коэффициентом теплопроводности окалины . На границе металл-окалина за счет действия сил трения происходит выделение теплоты. Между слоем окалины и оправкой происходит кондуктивный теплообмен (теплопроводностью). Между слоем окалины и металлом осуществляется как кондуктивный теплообмен, так и лучистый теплообмен через воздушную среду, заполняющую прослойку. При этом воздух считается диатермической средой, то есть прозрачной для лучистой энергии. Теплофизические свойства воздуха характеризуются коэффициентом теплопроводности воздуха .

Начальные (временные) условия.

Рассматриваемый процесс является нестационарным, то есть в уравнения входит время в качестве переменной. Для такого процесса необходимы начальные условия, которые состоят в задании закона распределения температуры внутри тела в начальный момент времени.

При первой прошивке начальное поле температур задается равномерным и равным температуре окружающей среды :

. (2.26)

При охлаждении оправки в качестве начального условия принимается температурное поле, полученное в конце нагрева оправки (в конце прошивки):

. (2.27)

Для второго и последующих циклов нагрева и охлаждения за начальное условие также принимается температурное поле предыдущего процесса теплообмена.

Граничные условия (на границе в нерегулярных узлах).

Применяются условия второго рода (условия Неймана): на поверхности задается плотность теплового потока как функция от температуры и координаты .

Граничные условия на границе металл - оправка при нагреве.

Граничные условия в области раздела деформируемый металл - оправка задаются через плотность теплового потока с учетом теплоты, выделяемой при работе сил трения и температурного сопротивления слоя окалины:

; (2.28)

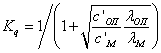,(2.29)

где  - плотность кондуктивного теплового потока в системе металл - окалина - заготовка;

 - плотность кондуктивного теплового потока в системе металл - воздух - оправка;

 - плотность лучистого теплового потока от металла к оправке в воздушном зазоре;

 - коэффициент контакта, равный отношению площади контакта ко всей площади поверхности оправки в данном сечении и определяемый экспериментально (в нашем случае на I участке , на II участке 0 <  < 1 (), а на III и IV участках - );  - плотность теплового потока за счет сил трения;  - коэффициент, учитывающий долю теплоты, поступающей на оправку

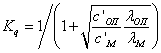. (2.30)

Граничные условия при охлаждении оправки (граничные условия третьего рода).

При расчете охлаждения оправки между прошивками применяются граничные условия третьего рода (используется температура окружающей среды  и коэффициент теплоотдачи ):

. (2.31)

 - плотность теплового потока с поверхности оправки при охлаждении, которая рассчитывается в зависимости от условий охлаждения. Например, при охлаждении на воздухе:

,(2.32)

где  - коэффициент теплоотдачи свободной конвекцией;  - температура поверхности оправки;  - температура охлаждающей среды (в данном случае воздуха).

При интенсивном охлаждении оправки

. (2.33)

В этом случае  - коэффициент теплоотдачи при вынужденной конвекции от поверхности оправки к потоку охладителя. Расчет коэффициента теплоотдачи выполняется по известным критериальным зависимостям.

Граничные условия на четвертом участке.

Граничные условия вдоль оси Oz на четвертом участке задаются при допущении отсутствия теплообмена на этой границе:

. (2.34)

2.2 Математическая формулировка задачи расчета температурного поля оправки

В общем виде уравнение теплопроводности записывается так:

,(2.35)

где  - температура,  - теплоемкость удельная массовая теплоемкость,  - коэффициент теплопроводности и  - плотность источников тепла.

Поскольку внутренних источников тепла нет, то уравнение записывается так:

. (2.36)

Поскольку прошивная оправка представляет собой тело вращения, то удобно использовать цилиндрическую систему координат. На первом участке для повышения точности решения применена сферическая система координат. Уравнение теплопроводности для сферической системы координат (участок I):

. (2.37)

Для цилиндрической системы координат (участки II, III и IV):

. (2.38)

В уравнениях  - цилиндрические координаты;  - сферические координаты;  - температура;  - время;  - удельная объемная теплоемкость;  - плотность материала оправки;  - удельная массовая теплоемкость.

Для центра сферы уравнение теплопроводности записывается следующим образом:

. (2.39)

Для оси центра:

. (2.40)

Для выделения единственного решения дифференциального уравнения применяются описанные выше условия однозначности (3), (4).

3. Метод и алгоритм решения уравнений теплообмена

Для решения дифференциального уравнения теплопроводности (2.36) с соответствующими начальными и граничными условиями применяется метод конечных разностей. Конечно-разностная сетка изображена на рис.3.1 Каждый узел сетки нумеруется в виде , где  - номер узла по направлению  для полусферы и цилиндра, a  - номер узла по направлению  для полусферы и по направлению  для цилиндра. Нумерация узлов начинается от центра сферы и оси цилиндра. Коническая поверхность оправки заменена ступенчатой, кратной шагу . Дискретные моменты времени обычно нумеруются индексами:  - предыдущий, а  - последующий моменты времени. Номер предыдущей и последующей итерации обозначается верхними индексами  и  соответственно.

Для аппроксимации дифференциальных уравнений теплопроводности (2.37) - (2.40) применяется неявная консервативная итерационная разностная схема, реализуемая методом Гаусса-Зейделя. Суть этого метода заключается в том, что при расчете температуры  в узле  на -й итерации используются температуры  и  из предыдущей итерации и вновь вычисленные температуры  и на расчетной -й итерации. Неявность разностной схемы достигается применением итерационной процедуры на каждом временном слое.

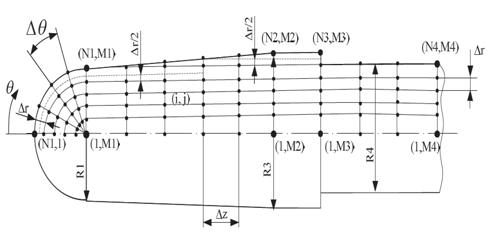
Рис.3.1 Конечно-разностная сетка, применяемая в численном методе конечных разностей при решении задачи теплопроводности оправки.

Конечно-разностные аналоги дифференциального уравнения теплопроводности для всех характерных участков оправки записываются так:

а) внутренние узлы сферы :

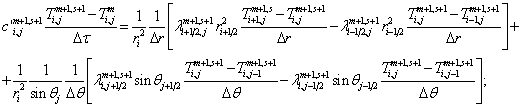(3.1)

б) внутренние узлы конической и цилиндрической частей оправки :

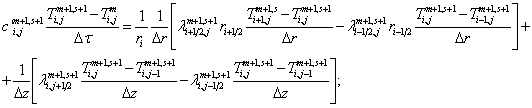(3.2)

в) температура в узлах, расположенных на поверхности сопряжения: полусфера - конус, рассчитывается следующим образом. Поскольку поверхность сопряжения одновременно принадлежит полусфере и конусу, то вторая производную по координатам  и  аппроксимируется по формулам, приведенным далее. Для полусферы принимается составляющая второй производной по углу  в сферических координатах, а для конической части - составляющая второй производной по в цилиндрических координатах. Узлы, расположенные на поверхности сопряжения полусфера - конус, пронумерованы . На поверхности сопряжения при использовании равномерной сетки уравнения записываются так:

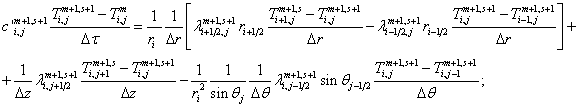(3.3)

г) узлы, расположенные на оси полусферы

(3.4)

д) узлы, расположенные на оси конической и цилиндрической частей оправки

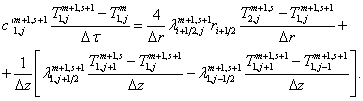(3.5)

При аппроксимации дифференциальных уравнений (2.39) и (2.40) конечно-разностными аналогами (3.3) и (3.4) учитывается, что в силу симметрии  и . В вышеприведенных формулах (3.1) - (3.4) принимаются следующие обозначения:

; (3.6)

; (3.7)

; (3.8)

; (3.9)

,(3.10)

где  - шаг по координате .

На поверхности оправки граничные условия II рода при нагреве (2.28) и охлаждении (2.31) аппроксимируются по трем приграничным узлам с учетом поглощения (выделения) теплоты в приграничном узле толщиной :

,(3.11)

где  - плотность теплового потока, поступающего на оправку при прошивке или уходящего с нее при охлаждении. Из последнего уравнения получается формула для определения температуры поверхности оправки в узлах :

. (3.12)

Граничное условие (2.58) на торцевой границе стержня также аппроксимируется по значениям температуры в трех приграничных узлах сетки

,(3.13)

откуда получается

. (3.14)

При расчете температуры в "центральной" точке сферы и усеченного конуса  возникают трудности, связанные с тем, что эта точка принадлежит одновременно центру полусферы и оси плоскости сопряжения полусфера - цилиндр. Температура в этой "центральной" точке определяется по балансу тепловой энергии в объеме, прилегающем к этой точке (рис.3.2):

,(3.15)

где  - удельная объемная теплоемкость; - объем тела вращения ABDSA;  - тепловой поток, поступающий в выделенный объем.

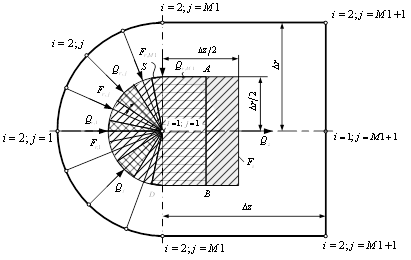
Рис.3.2 Пояснение к расчету температурного поля в центре сферического участка.

Тепловой поток равен

,(3.16)

где составляющие теплового баланса определяются по формулам

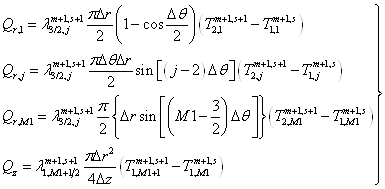. (3.17)

Объем тела вращения ABDSA (см. рис.3.2) рассчитывается по формуле

. (3.18)

В общем случае все конечно-разностные уравнения приводя