Скачать

Методические указания и контрольные задания для студентов-заочников

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

Федеральное государственное образовательное учреждение высшего профессионального образования

МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Мончегорский филиал

ВЫСШАЯ МАТЕМАТИКА.

Методические указания и контрольные задания для студентов-заочников специальности 061100 «Менеджмент организации»

Мончегорск 2005г.

Общие организационно-методические указания

Основные задачи при изучении курса «Высшая математика»:

· освоение наиболее употребительных понятий и определений математики;

· изучение основ линейной алгебры, математического анализа, дифференциальных уравнений;

· приобретение практических навыков в решении задач.

Учебными планами для студентов-заочников предусмотрены лекции, практические занятия с преподавателями, самостоятельная работа и выполнение контрольных работ. При изучении теоретического материала рекомендуется составлять краткие конспекты тем и ответить на вопросы для самопроверки, приведенные в конце каждой темы.

 Программа курса рассчитана на два семестра. В каждом семестре необходимо выполнить две контрольные работы. В конце каждого семестра проводится экзамен.

Тематический план осеннего семестра

1. Множества. Числа.

2. Линейная алгебра.

3. Аналитическая геометрия.

4. Функции.

5. Комплексные числа. Многочлены.

6. Предел и непрерывность функции.

7. Дифференциальное исчисление.

Тематический план весеннего семестра.

1. Неопределенный интеграл.

2. Определенный интеграл.

3. Ряды.

4. Функции многих переменных.

5. Дифференциальные уравнения.

Рекомендуемая литература

1. Кремер Н.Ш,.и др. Высшая математика для экономистов/Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.- М.: Банки и биржи, 1997. – 439с.

2. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики: Учеб. пособие для вузов. – 2-е изд., перераб. и доп., – Высш. шк., 1972. – 480 с.

3. Шипачев В.С. Основы высшей математики. М.: Высшая школа, 1989.

4. 4.Красс М.С. Математика для экономических специальностей: Учебник. – М.: ИНФРА-М, 1998. – 464с. – (Серия “Высшее образование”).

5. Дополнительная

6. Ивашев-Мусатов О.С. Начала математического анализа: Учеб. пособие для вузов. – 4-е изд., испр. – М. : Наука, 1981. – 159с.

7. Пискунов Н.С. Дифференциальное и интегральное исчисления: В 2 т.: Учеб. пособие для втузов. – М. : Наука, 1978. Т.1– 453с., Т.2 – 575с..

6. Мордкович А.Г., Смышляев В.К..Алгебра и начало анализа. М.: Просвещение, 1987

8. Фихтенгольц Г.М. Основы математического анализа М. Наука 1968

9. Виленкин И.В. Гробер В.М. Высшая математика Ростов–на-Дону “Феникс” 2002

10. Ермаков В.И. Общий курс высшей математики для экономистов М. ИНФРА – М 2003

11. Письменный Д.Т. Конспект лекций по высшей математике М. АЙРИС ПРЕСС 2004

12. Данко П.Е. Попов А.Г. Высшая математика в упражнениях и задачах М. Высшая школа 1999.

ТЕМА 1. МНОЖЕСТВА, ЧИСЛА

Понятие множества. Подмножество, объединение, пересечение, дополнение. Числовые множества: натуральные, целые, рациональные, действительные числа. Модуль числа. Интервал, окрестность, отрезок. Числовая ось.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Множеством называется совокупность каких-либо объектов, обладающих общим для них характеристическим свойством. Эти объекты называются элементами множества. Если элемент а принадлежит множеству А, то пишут аÎА, если не принадлежит , аÏА. множество может состоять как из конечного, так и бесконечного числа элементов. множество, не содержащее ни одного элементы, называется пустым и обозначается О. Если каждый элемент множества А является одновременно элементом множества В, то множество а называется подмножеством множества В. Множество С, состоящее из элементов, каждый из которых принадлежит одновременно множеству А и множеству В, называется пересечением множеств А и В, обозначается С=А∩В. Множество С, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств А и В, называется объединением А и В ( обозначается А U В).

если множество А является подмножеством В, то дополнением подмножества А до множества В называется множество D, состоящее из элементов, принадлежащих В, но не принадлежащих А ( обозначается D= В\А). N - множество натуральных чисел. Z -множество целых чисел. N подмножество Z: NÌ Z . Q: m/n -множество рациональных чисел. I -множество иррациональных чисел. Q U I = R, R- множество действительных чисел. Геометрическое изображение R - это множество точек числовой прямой. (а,в) - отрезок : а£´£в.

( а,в)- интервал : а< ´< в.

аÎ R , вÎ R .

Вопросы для самопроверки.

1. Приведите примеры множеств, состоящих из конечного и из бесконечного числа элементов.

2. Сколько подмножеств можно образовать из множества Х={ х₁, х₂, х₃}?

3. Изобразите на бумагу два множества в виде двух частично перекрывающихся геометрических фигур (каждое множество состоит из точек, расположенных внутри соответствующей фигуры). Заштрихуйте объединение и пресечение множеств.

4. Приведите пример числового множества, состоящего из конечного числа элементов.

5. Какое из чисел больше6 –5 или 3? У какого из этих чисел больше модуль?

6. Приведите примеры интервала и отрезка. Чем отличается отрезоу от интервала?

7. Изобразите на числовой оси числа 2, ½, -1.

8. При каких х справедливо равенство |x³|= - x³?

ТЕМА 2. ЛИНЕЙНАЯ АЛГЕБРА

Векторы в n-мерной системе координат. Матрицы. Определитель. Ранг матрицы. Сложение матриц. Умножение матрицы на вектор. Умножение матрицы на матрицу, коммутативность. Диагональная и единичная матрицы, транспонированная матрица. Треугольная матрица. Обратная матрица. Системы линейных алгебраических уравнений. Условия существования и единственности решения. Формула Крамера. Метод Гаусса.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

В некоторых приложениях употребляется n-мерная прямоугольная система координат, в которой формально введены не2 или 3, а n взаимно перпендикулярных координатных осей. Вектор в такой системе – это набор из n упорядоченных чисел – координат вектора.

Базис и координаты вектора.

. Линейной комбинацией векторов а_1, а₂,…,а_n называется выражение вида: k₁a₁ + k₂a₂ +…+ k_na_n, где k_i – числа.

Векторы а_1, а₂,…,а_nназываются линейно зависимыми, если найдутся такие числа k₁, k₂,…, k_n, не все равные нулю, что соответствующая линейная комбинация векторов равна нулю, т.е. k₁a₁ + k₂a₂ +…+ k_na_n = 0. Если же равенство возможно только при всех k_i = 0, векторы называются линейно независимыми.

Замечание 1. Если система векторов содержит нулевой вектор, то она линейно зависима.

Замечание 2. Если среди n векторов какие-либо (n-1) линейно зависимы, то и все n векторов линейно зависимы.

Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Рассмотрим декартову систему координат, базис которой образуют в пространстве три попарно ортогональных единичных вектора i, j, k. Тогда любой вектор d может быть представлен в виде их линейной комбинации:

d = Xi + Yj +Zk.

Числа X, Y, Z называются декартовыми координатами вектора d.

Замечание. Декартовы координаты вектора равны его проекциям на оси Ох, Оу и Оz декартовой системы координат.

Матрицей А=||a_ij || размера n´m называется прямоугольная таблица чисел.

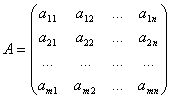
Обозначения: А – матрица,  - элемент матрицы,  номер строки, в которой стоит данный элемент,  номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Числа m и n называются размерностями матрицы.

Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы. Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:

.

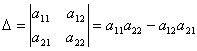При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

Примеры.

1.  2.

Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

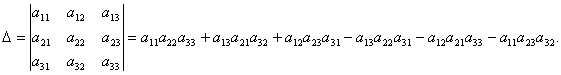
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:

Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.

 Матрица называется нулевой, если все ее элементы равны 0.

 Квадратная матрица называется единичной, если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0.

Линейные операции над матрицами.

1. Сложение матриц.

Суммой матриц А и В одинаковой размерности mn называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах:

Свойства сложения:

1. А + В = В + А.

2. (А + В) + С = А + (В + С) .

3. Если О – нулевая матрица, то А + О = О + А = А

Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.

Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.

Пример.

2. Умножение матрицы на число.

Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

Свойства умножения матрицы на число:

1. (km)A=k(mA).

2. k(A + B) = kA + kB.

3. (k + m)A = kA + mA.

Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.

Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С + В =А, т.е. С = А + (-1)В.

Пример.

. Тогда

Перемножение матриц.

Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго.

Произведением матрицы А размерности mp и матрицы В размерности  называется матрица С размерности , каждый элемент которой  определяется формулой:  Таким образом, элемент  представляет собой сумму произведений элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В.

Пример.

. При этом существует произведение АВ, но не существует произведение ВА. Размерность матрицы С=АВ составляет  Найдем элементы матрицы С:

Итак,

Обратная матрица.

Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

Cпособ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Линейными операциями над какими-либо объектами называются их сложение и умножение на число.

 Линейной комбинацией переменных называется результат применения к ним линейных операций, т.е.  где числа, переменные.

Линейным уравнением называется уравнение вида

где  и b – числа, - неизвестные.

Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.

Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.

Системой линейных уравнений (линейной системой) называется система вида

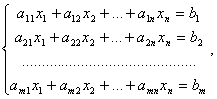
где , - числа, - неизвестные, n – число неизвестных, m – число уравнений.

 Решением линейной системы (2) называется набор чисел

 которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.

Метод Гаусса решения линейных систем.

Замечание. Линейная система может иметь единственное решение, бесконечно много решений или не иметь ни одного решения.

Способы нахождения единственного решения системы,

в которой число уравнений равно числу неизвестных: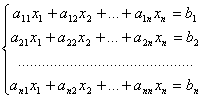

Пусть  (этого всегда можно добиться, поменяв уравнения местами). Разделим обе части первого уравнения на  и вычтем полученное уравнение из каждого из остальных уравнений системы, умножив его предварительно на  где i – номер очередного уравнения. Коэффициенты при  во всех уравнениях этой системы, начиная со второго, будут равны 0, т.е. система выглядит так:

.

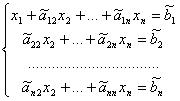Если новые коэффициенты при х₂ не все равны нулю, можно таким же образом исключить  из третьего и последующих уравнений. Продолжая эту операцию для следующих неизвестных, приведем систему к так называемому треугольному виду:

.

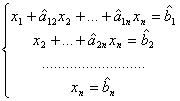Здесь символами  и  обозначены изменившиеся в результате преобразований числовые коэффициенты и свободные члены.

Из последнего уравнения системы единственным образом определяется , а затем последовательной подстановкой – остальные неизвестные.

Замечание. Иногда в результате преобразований в каком-либо из уравнений обращаются в 0 все коэффициенты и правая часть, то есть оно превращается в тождество 0=0. Исключив его из системы, мы уменьшим число уравнений по сравнению с числом неизвестных. Такая система не может иметь единственного решения.

Если же в процессе применения метода Гаусса какое-нибудь уравнение превратится в равенство вида 0=1 (коэффициенты при неизвестных обратились в 0, а правая часть приняла ненулевое значение), то исходная система не имеет решения, так как подобное равенство является неверным при любых значениях неизвестных.

Правило Крамера.

Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель , элементами которого являются коэффициенты при неизвестных:

 .

Правило Крамера позволяет найти единственное решение системы или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

2) Если  система (2.3) имеет единственное решение, определяемое по формулам: .

3) Если ==0, система имеет бесконечно много решений.

4) Если =0, а хотя бы один из  система не имеет решений.

Совместность линейных систем.

Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Вопросы для самопроверки.

1. Как характеризуется вектор в n-мерной прямоугольной системе координат?

2. Чему равно скалярное произведение двух векторов?

3. Как определяется местоположение элемента в матрице?

4. Что такое единичная матрица?

5. Что такое транспонированная матрица?

6. Каким требованиям должны удовлетворять перемножаемые матрицы?

7. Что такое обратная матрица?

8. Как находить решение системы линейных алгебраических уравнений с помощью формулы Крамера?

9. Как находить решение системы линейных алгебраических уравнений методом Гаусса?

ТЕМА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Понятие скаляра и вектора. Модуль вектора. Операции со скалярами и векторами. Скалярное произведение. Прямоугольная система координат на плоскости и в пространстве. Расстояние между точками. Уравнения прямой на плоскости. Пересечение прямых. Прямая, проходящая через две данные точки. Прямая, параллельная и препендикулярная данной прямой. Уравнение плоскости. Кривые второго порядка: эллипс, гипербола, парабола.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Скаляром называется величина, полностью характеризующаяся своим численным значением. Вектором называется направленный отрезок прямой. Обозначается , .Отрезок имеет начало и конец, направление вектора указывается стрелкой. Величина, равная длине вектора, называется модулем (абсолютной величиной вектора) вектора а и обозначается |а|. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.

Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Линейные операции над векторами.

Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а

Свойства сложения:

Свойство 1. a + b = b + a.

Свойство 2. (a+b)+c=a+(b+c). b

Свойство 3. Для любого вектора a существует нулевой вектор О такой, что a+О=а.

Свойство 4. Для каждого вектора a существует противоположный ему вектор a^/ такой, что а+а^/=О.

Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

Свойства умножения вектора на число:

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.

Скалярное произведение векторов.

Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

ab = |a||b| cosφ . Обозначения скалярного произведения: ab, (ab), a·b .

Если векторы а и b определены своими декартовыми координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂},

то ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ .

Пусть на плоскости задана декартова система координат и некоторая линия L.

Уравнение Ф(х,у) = 0 называется уравнением линии L, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты ни одной точки, не лежащей на линии L.

Прямая на плоскости.

,

каноническое уравнение прямой.

 -

уравнение прямой, проходящей через две заданные точки.

Обозначив за t значения равных дробей, стоящих в левой и правой частях уравнения

можно преобразовать это уравнение к виду:

x = x₀ + lt, y = y₀ + mt -

параметрические уравнения прямой.

Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k – тангенс угла, образованного прямой и осью Ох, и записать уравнение

прямой в виде:

у = kx + b -

уравнение прямой с угловым коэффициентом.

Действительно, все точки прямой l₁, параллельной l и проходящей

через начало координат, удовлетворяют уравнению у = kх, а ординаты соответствующих точек на прямой l отличаются от них на постоянную величину b.

Неполные уравнения прямой.

1) С = 0 - прямая Ах + Ву = 0 проходит через начало координат.

2) В = 0 - прямая Ах + С = 0 параллельна оси Оу (так как нормаль к прямой {A,0} перпендикулярна оси Оу).

3) А = 0 - прямая Ву + С = 0 параллельна оси Ох.

4) В=С=0 – уравнение Ах = 0 определяет ось Оу.

5) А=С=0 – уравнение Ву = 0 определяет ось Ох.

где  и  равны величинам отрезков, отсекаемых прямой на осях Ох и Оу. Уравнение прямой в отрезках.

Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.

1. Если прямые L₁ и L₂ заданы общими уравнениями

А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0,

то

.

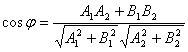2. Если прямые заданы каноническими уравнениями, по аналогии с пунктом 1 получим:

,

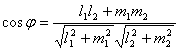 - условие параллельности,

 - условие перпендикулярности.

Здесь  и - направляющие векторы прямых.

3. Пусть прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами

у = k₁x +b₁ и y = k₂x + b₂, где , а α₁ и α₂ – углы наклона прямых к оси Ох, то для угла φ между прямыми справедливо равенство: φ = α₂ - α₁. Тогда

 .

Условие параллельности имеет вид: k₁=k₂,

условие перпендикулярности – k₂=-1/k₁, поскольку при этом tgφ не существует.

Расстояние от точки до прямой.

Рассмотрим прямую L и проведем перпендикуляр ОР к ней из начала координат (предполагаем, что прямая не проходит через начало координат).

Расстояние от точки до прямой определяется так:

Замечание. Для того, чтобы привести общее уравнение прямой к нормальному виду, нужно умножить его на число , причем знак выбирается противоположным знаку свободного члена С в общем уравнении прямой. Это число называется нормирующим множителем.

Пример. Найдем расстояние от точки А(7,-3) до прямой, заданной уравнением

3х + 4у + 15 = 0. А² + B²=9+16=25, C=15>0, поэтому нормирующий множитель равен

-1/5, и нормальное уравнение прямой имеет вид:  Подставив в его левую часть вместо х и у координаты точки А, получим, что ее отклонение от прямой равно

 Следовательно, расстояние от точки А до данной прямой равно 4,8.

Расстояние между двумя точками М(х,у,z) и N( х₁,у₁,z₁) выражается формулой

d(MN) = (х₁ – x)² + (у₁ – y)² + (z₁ – z)²

Плоскость в пространстве.

A(x - x₀) + B(y - y₀) + C(z - z₀) = 0.

уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

После приведения подобных можно записать уравнение в виде:

Ax + By + Cz + D = 0,

где D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.

уравнение плоскости в отрезках.. Параметры а, b и с равны величинам отрезков, отсекаемых плоскостью на координатных осях.

Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

Косинус угла между плоскостями α₁ и α₂ равен

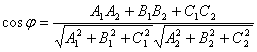
Условие параллельности плоскостей заключается в параллельности нормалей:

а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:

A₁A₂ + B₁B₂ + C₁C₂ = 0

Прямая в пространстве.

Замечание. Прямую в пространстве невозможно задать одним уравнением. Для этого требуется система двух или более уравнений.

 Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями

A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0, где коэффициенты A₁,B₁,C₁ и A₂,B₂,C₂ не пропорциональны:

A₁x+B₁y+C₁z+D₁=0 A₂x+B₂y+C₂z+D₂=0.

Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.

Составим уравнения прямой, проходящей через точку М₀(x₀,y₀,z₀) параллельно вектору a={l,m,n}.

Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.

Для любой точки М(x,y,z), лежащей на данной прямой, вектор М₀М = {x - x₀,y - y₀,z - z₀) коллинеарен направляющему вектору а. Поэтому имеют место равенства:

называемые каноническими уравнениями прямой в пространстве.

В частности, если требуется получить уравнения прямой, проходящей через две точки:

М₁(х₁, у₁, z₁) и M₂(x₂, y₂, z₂), направляющим вектором такой прямой можно считать вектор М₁М₂ = {x₂ – x₁, y₂ - y₁, z₂ - z₁}, и уравнения (8.11) принимают вид:

 -

- уравнения прямой, проходящей через две данные точки.

Если же принять каждую из равных дробей в уравнениях (8.11) за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:

 .

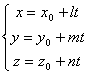Угол между прямыми. Угол между прямой и плоскостью.

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

 и  косинус угла между ними можно найти по формуле:

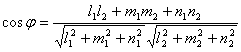 . (8.14)

Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:

 - условие параллельности прямых, (8.15)

 - условие перпендикулярности прямых. (8.16)

Угол φ между прямой, заданной каноническими уравнениями

 и плоскостью, определяемой общим уравнением

Ax + By + Cz + D = 0, можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда

Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:

Al + Bm + Cn = 0,

а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n.

Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Эллипс.

Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

каноническое уравнение эллипса:

Эксцентриситетом эллипса называется величина е=с/а

b² = a²-c²

Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением, а уравнением второй степени другого .

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса e < 1.

Действительно,

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е<1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике )

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Гипербола.

Гиперболой называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

 - каноническое уравнение гиперболы.

Эксцентриситетом гиперболы называется величина е = с / а.

Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

 и .

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

 ,

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Парабола.

Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

y²=2px ,

каноническое уравнение параболы. Величина р называется параметром параболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e<1), гиперболу (при e>1) или параболу (при е=1).

Приведение уравнения второго порядка к каноническому виду.

Линия, определяемая общим уравнением второго порядка

,

называется алгебраической линией второго порядка.

Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:

1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);

2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).

Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной пара

Классификация кривых второго порядка.

Рассмотрим общее уравнение второго порядка

и выясним, какие геометрические образы на плоскости могут задаваться этим уравнением.

 - каноническое уравнение эллипса.

 или , в зависимости от знака . Оба этих уравнения определяют гиперболу.

б) При =0 получаем уравнение , эквивалентное двум линейным уравнениям: и , задающим пару пересекающихся прямых.

а) к уравнению (11.8): , определяющему параболу;

б) к уравнению , или , задающему пару параллельных прямых;

в) к уравнению , определяющему одну прямую (или пару совпадающих прямых);

г) к уравнению