Скачать

Метод конечных элементов

Основные положения метода конечных элементов и суперэлементов

Метод конечных элементов (МКЭ) занимает исключительное место в теории расчета конструкций, а его обобщение – метод суперэлементов – позволяет естественным образом ввести и описать идеею иерархически построенных сложных систем.

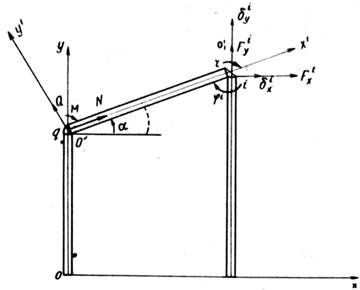Рассмотрим плоскую раму каркаса промышленного здания, стойки которой жестко защемлены в фундаментах, а ригели жестко прикреплены к стойкам. Ограничим рассмотрение случаем, когда на раму действует только узловая нагрузка. Пронумеруем узлы – точки пересечения осей стержней друг с другом и “землей”. В каждом узле i рамы на нее могут действовать сосредоточенные силы Fx, Fy и момент М, заданные в некоторой глобальной системе координат, связанной с рамой.

Введем в рассмотрение вектор {Fi} обобщенных сил, действующих на раму в узле i

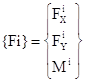(1)

Совокупность внешних воздействий на всю раму будет характеризоваться вектором {F}:

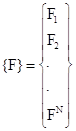(2)

Где N-число узлов рамы. Размерность этого вектора 3хN (пока не учитываем факт прикрепления некоторых узлов к “земле”). Под действием внешних сил {F} стержни рамы получают деформации, а узлы переместятся. После перемещения узлов рамы будем описывать в глобальной системе координат. Перемещения {di} каждого узла характеризуется тремя числами – линейными перемещениями dxi, dyi и углом поворота ji, являющимися компонентами вектора обобщенных перемещений узла di:

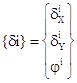(3)

А перемещения всей рамы вектором d:

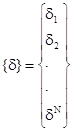(4)

Здесь, как и выше, не учитываются условия закрепления стоек рамы и узлов.

Напряженно-деформированное состояние каждого стержня удобнее характеризировать в локальной системе координат, связанной с ним. Ось х’ этой системы координат направим от “начала” q стержня к его “концу” r (понятие “начало” и ‘конец” условны и нужны только для того, чтобы задать положительное направление на оси х’), ось у’ – в плоскости рамы, а ось z’ – перпендикулярно плоскости. Положительные направления осей y’ и z’ выберем так, чтобы они образовывали с x' правую систему координат.

Проведем в каждом стержне рамы по 2 поперечных сечения на расстоянии, бесконечно близких к узлам – концам стержней q и r. В каждом из полученных решений в общем случае действуют три усилия N, Q, M, приложенные к узлу. Введем вектор обобщенных усилий в сечении с’ стержня m:

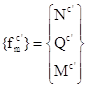(5)

И вектор усилий {fm}, характеризующий напряженное сечение стержня m через векторы усилий в его концевых стержнях q и r (“начале ” и “конце”)

(6)

(штрих означает, что компоненты {fm’} вычислены в локальной системе координат).

Вектор {fm’} полностью характеризует напряженно-деформированное состояние стержня, если к его внутренним точкам не приложены внешние воздействия и известны жесткостные характеристики стержня. Разумеется шесть компонент вектора {fm’} связаны между собой уравнениями равновесия стержня как жесткого тела, но эти уравнения в явном виде далее не используются.

Напряженно-деформированное состояние того же стержня характеризуется и вектором обобщенных перемещений концов стержня q и r, который строится из соответствующих компонент вектора, см. выражение (4):

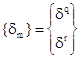(7)

Отметим, что при таком введении вектора обобщенных перемещений стержня его напряженно деформированное состояние зависит не только от значений {dm}, но и от способов прикрепления стержня m к узлам q и к и его жесткости.

Например, если бы конец q ригеля был присоединен к стойке шарнирно, то усилие М в сечении q было бы равно нулю, независимо от значений компонент {dm}.

Компоненты вектора {fm’} заданны в локальной системе отсчета, а компоненты вектора {dm} – в глобальной. Для установления связи векторов {fm’} и {dm} в простейшем виде запишем компоненты {dm} тоже в локальной системе отсчета, связанной с рассматриваемым стержнем. Обозначим матрицу преобразования координат

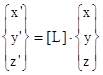(8)

через (L):

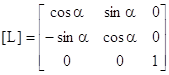(9)

Тогда, например, компоненты вектора в локальной системе координат запишутся в виде

(10)

Аналогично компоненты вектора в глобальной системе отсчета связаны с компонентами , соотношением

(11)

Векторы обобщенных усилий и перемещений для стержня, выраженные в локальной и глобальной системах отсчета, связаны соотношением

, (12)

где матрица (Λ) имеет вид

(13)

Введем матрицу жесткости стержня (km’), характеризующую связь между векторами {fm’} и {dm}

(14)

Способ получения матрицы жесткости (km’) является предметом особого рассмотрения. Конкретные примеры вычисления отдельных компонент матрицы (km’) для стержней с различными условиями закрепления узлов приводятся в курсах строительной механики. Физическая сущность процесса получения матрицы (km’) заключается в необходимости решения задач строительной механики для отдельного стержня- получения вектора усилий в концевых сечениях стержня по заданным перемещениям концов стержней (краевая задача первого рода) или получение вектора перемещений концов стержня по заданным силовым воздействиям на его концах (краевая задача второго рода). Для стержневых элементов с жесткостью, постоянной по длине, задача решается в замкнутом виде и матрица (km’) известна. Для физических элементов более общего вида – пластинчатых различного очертания, оболочечных, сложных элементов, являющихся композицией элементов, более простых, - процедура получения матрицы (km’) сводится к фактическому решению той или иной задачи строительной механики или механики сплошной среды. Как правило решить эту задачу в общем виде на удается и матрица жесткости (km’) строится численно для каждого из образующих конструкцию элементов.

В дальнейшем предполагается, что матрица (km’) известна. Для стержня, оба конца которого жестко прикреплены к узлам, она имеет вид:

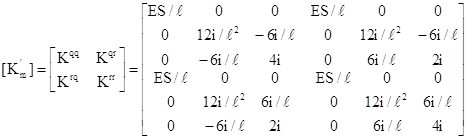(15)

где Е-модуль упругости материала стержня; S-площадь поперечного сечения; J-момент инерции сечения; I=EJ/ll-длина стержня.

Фактический смысл компонент и блоков матрицы (km’) ясен. Блок (Kqq) и его компоненты характеризуют усилия, возникающие в сечении q стержня при смещении узла q, а блок (Kqr) и его компоненты – усилия в сечении q стержня при смещении узла r. В зависимости от ориентации систем отсчета и правила знаков при определении усилий могут изменятся знаки некоторых компонент матрицы (K’m).

Основное соотношение (15) позволяет выразить усилия в концевых сечениях каждого стержня через перемещения его концов – узлов системы. С другой стороны, усилия в концевых сечениях стержней с точностью до знака равны силам, действующим со стороны стержней на узлы, поэтому матрица (K’m) позволяет связать перемещения узлов стержневой системы с силами, с которыми стержни действуют на узлы при перемещениям последних.

Запишем систему равновесия узлов. Для узла имеем систему трех уравнений равновесия:

(16)

где суммирование распространяется на все стержни, сходящиеся в узле i, а с обозначает сечение каждого их этих стержней, бесконечно близкое к узлу. Число этих уравнений равно числу неизвестных перемещений узла. Но поскольку величины {fm^c}зависят не только от перемещений указанного узла, но, в силу (14)-(15), и от перемещений соседних узлов, с которыми узел i связан хотя бы одним стержнем, то уравнение (16) для узла i входят и перемещения соседних узлов. Чтобы определить перемещения соседних узлов, системы уравнения типа (16) надо записать для всех узлов системы и решать их совместно.

Уравнение (16) удобно записывать в глобальной системе отсчета, а связь (14) установлена в локальной системе координат, связанных с отдельными стержнями.

Чтобы работать постоянно в глобальной системе координат, выразим связь (14) в глобальной системе координат с помощью соотношений (10)-(13):

. (17)

Умножим это равенство слева на (Λ)^-1 и учтите при этом, что в силу ортогональности (Λ) имеет место равенство

(18)

Тогда

(19)

Выражение (19) определяет матрицу (Km) в глобальной системе координат.

Перепишем (16), используя обозначения блоков (15) матрицы

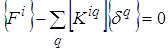(20)

где суммирование распространяется на все стержни, соединяющиеся с узлом i. Полная система уравнений равновесия для стержневой системы с N узлами в матричной форме примет вид:

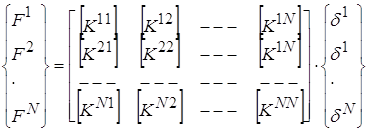
(21)

Если какой-либо узел Р на связан ни с одним стержнем с узлом r, то блок (K^pr) в матрице (21) будет тождественно равен нулю. Таком образом, умея вычислять блоки (K^qq) и (K^qr) для отдельных стержней, на основании информации о системе в целом можно построить систему уравнений равновесия (21) относительно искомых перемещений {d}. Вектор внешних сил {F} предполагается известным.

Наличие опорных закреплений приводит к тому, что некоторые компоненты вектора d заранее известны. Соответствующие компоненты должны быть исключены из искомого вектора {d}, равно как и столбцы с теми же номерами из матрицы (21). Уравнение равновесия для закрепленных узлов не составляются, что равносильно уменьшению числа уравнений (числа строк в матрице) системы (21).

После этого можно решить систему (21) относительно {d}. Обычно для решения используются прямые методы, типа метода последовательного исключения неизвестных Гаусса. Найдя {d}, по формулам (14) или (19) можно определить усилия во всех стержневых элементах системы, в том числе и стержнях, примыкающим к опорным узлам. На этом заканчивается этап статического расчета стержневой конструкции.

Литература:

Геммерлинг Г.А. Система автоматизированного проектирования стальных строительный конструкций. – М.: Стройиздат, 1987г.