Скачать

Место и роль математики в менеджменте и экономике

Государственный университет экономики статистики и информатики

Реферат

по предмету: Высшая математика

на тему: Место и роль математики в менеджменте и экономике

Глава 1. Развитие понятия функции

Изучение свойств функции и построение ее графика являются одним из самых замечательных приложений производной. Этот способ исследования функции неоднократно подвергался тщательному анализу. Основная причина состоит в том, что в приложениях математики приходилось иметь дело со все более и более сложными функциями, появляющимися при изучении новых явлений. Появились исключения из разработанных математикой правил, появились случаи, когда вообще созданные правила не годились, появились функции, не имеющие ни в одной точке производной.

Развитие функциональных представлений в курсе изучения алгебры и начал анализа на старшей ступени обучения помогает получить наглядные представления о непрерывности и разрывах функций, узнать о непрерывности любой элементарной функции на области ее применения, научиться строить их графики и обобщить сведения об основных элементарных функциях и осознать их роль в изучении явлений реальной действительности, в человеческой практики.

Начиная с XVIII века одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.

Необходимые предпосылки к возникновению понятия функции были созданы, когда возникла аналитическая геометрия, характеризующаяся активным привлечением алгебры к решению геометрических задач.

Идея функциональной зависимости возникла в глубокой древности. Она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур и геометрических тел.

Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берет свое начало в XVII веке в связи с проникновением в математику идеи переменных.

Четкого представления понятия функции в XVII веке еще не было, однако путь к первому такому определению проложил Декарт. Постепенно понятие функции стало отождествляться с понятием аналитического выражения – формулы.

Явное определение функции было впервые дано в 1718 году Иоганном Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».

Во второй половине XIX века понятие функции формулируется следующим образом: если каждому элементу х множества А поставлен в соответствие некоторый определенный элемент у множества В, то говорят, что на множестве А задана функция y = f(x), или что множество А отображено на множество В.

Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам, например, к геометрическим фигурам.

Краткий обзор развития понятия функции приводит к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом.

2.1 Определение функции и графика функции. Область определения и область значений функции. Нули функции

функция график экономический

Умение изображать геометрически функциональные зависимости, заданные формулами, особенно важно для успешного усвоения курса высшей математики.

Как известно, функциональной зависимостью называют закон, по которому каждому значению величины х из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины у; совокупность значений, которые принимает зависимая переменная у, называется областью изменения функции.

Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x).

Функцию можно задать тремя способами: аналитический, табличный, графический.

Аналитический – с помощью формул.

Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента.

Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.

Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.

Пример 1. Найти область определения функции

y = lg (2x-3) у = lg(2x-3)

D(y): 2x-3 > 0

2x > 3

х > 1,5

Ответ: D(y) = (1,5; +∞ ).

Одним из понятий для исследования функции является нули функции.

Нули функции – это точки, в которых функция принимает значение нуля.

Пример 2. Найти нули функции

y = 4x-8

у = 4x-8

D(y) = R

По определению:

у = 0,

тогда

4х-8 = 0

4x = 8

х = 2

Ответ: нулями этой функции является точка х = 2.

2.2 Виды функций (четные, нечетные, общего вида, периодические функции)

Рассмотрим функции, области определения которых симметричны относительно начала координат, то есть для любого х из области определения число (-х) также принадлежит области определения. Среди таких функций выделяют четные и нечетные.

Определение: Функция f называется четной, если для любого х из ее области определения f(-x) = f(x).

График четной функции симметричен относительно оси ординат.

Пример 3. Определить вид функции

y = 2cos2x.         

у = 2cos2x,

D(y) = R

y(-x) = 2cos2(-x) = -2cos2x = 2cos2x = y(x) – четная.

Пример 4. Определить вид функции

y = x4 - 2x2 + 2.

Y = x4 - 2x2 + 2,

D(y) = R.

y(-x) = (-x)4 - 2(-x)2 + 2 = x4 - 2x2 + 2 = y(x) – четная.

Определение: Функция f называется нечетной, если для любого х из ее области определения f(-x) = -f(x).

График нечетной функции симметричен относительно начала координат.

Пример 5. Определить вид функции

y = 2sin2x.

у = 2sin2x,

D(y) = R

y(-x) = 2sin2(-x) = -2sin2x = -y(x) – нечетная.

Пример 6. Определить вид функции

y = 3x + 1/3x.

у = 3x + 1/3x

y(-x) = 3(-x) + 1/3(-x) = -3x - 1/3x = -(3x + 1/3x) = -y(x) – нечетная.

Определение: Функцию f называют периодической с периодом Т≠ 0, если для любого х из области определения значения этой функции в точках х, х -Т и х+Т равны, то есть f(x+T) = f(x) = f(x-T).

Пример 7. Определить период функции

y = cos2x.

cos2x = cos2(x+T) = cos(2x+2T),

где 2T = 2π, т.е. Т = π.

Для построения графика периодической функции с периодом Т достаточно провести построение на отрезке длиной Т и затем полученный график параллельно перенести на расстояния nT вправо и влево вдоль оси Ох.

Пример 8. Построить график периодической функции

f(x) = sin2x.

f(x) = sin2x,

sin2x = sin2(x+T) = sin(2x+2T),

где 2Т = 2π, т.е. Т = π.

2.3 Возрастание и убывание функций. Экстремумы

Также к свойствам функции относятся возрастание и убывание функции, экстремумы.

Функция f возрастает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 > х1 , выполнено неравенство f(x2) > f(x1).

Функция f убывает на множестве Р, если для любых х1 и х2 из множества Р, таких, что х2 > х1 , выполнено неравенство f(x2) < f(x1).

Иными словами, функция f называется возрастающей на множестве Р, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве Р, если большему значению аргумента соответствует меньшее значение функции.

При построении графиков конкретных функций полезно предварительно найти точки минимума (xmin) и максимума (xmax).

Точка х0 называется точкой максимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ≤ f(x0).

Точка х0 называется точкой минимума функции f , если для всех х из некоторой окрестности х0 выполнено неравенство f(x) ≥ f(x0).

Точки минимума и максимума принято называть точками экстремума.

Пример 9. Найти точки экстремума, экстремумы функции y = x2+2x, и указать промежутки возрастания и убывания функции.

у = x2+2x, D(y) = R

y’ = (x2+2x)’ = 2x+2

y’ = 0, т.е. 2х+2 = 0

2х = -2

х = -1

Исследуем знак производной справа и слева от крайней точки.

x = -2, y’= -4+2<0

x = 0, y’= 0+2>0

Так как производная меняет свой знак с «-» на «+», то х = -1, это точка минимума функции. Так как функция непрерывна в точке х = -1, то функция возрастает на (-1;+∞) и убывает на (-∞;-1).

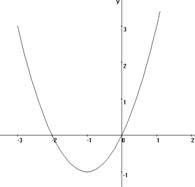
Точки экстремума: xmin = -1

Экстремумы функции: ymin = y(-1) = 1 – 2 = -1

3.1 Общая схема исследования функций

Исследуя функцию, нужно знать общую схему исследования:

1) D(y) – область определения (область изменения переменной х)

2) E(y) – область значения х (область изменения переменной у)

3) Вид функции: четная, нечетная, периодическая или функция общего вида.

4) Точки пересечения графика функции с осями Ох и Оу (по возможности).

5) Промежутки знакопостоянства:

а) функция принимает положительное значение : f(x) > 0

б) отрицательное значение : f(x) < 0.

6) Промежутки монотонности функции:

а) возрастания;

б) убывания;

в) постоянства ( f = const).

7) Точки экстремума (точки минимума и максимума)

8) Экстремумы функции (значение функции в точках минимума и максимума)

9) Дополнительные точки.

Они могут быть взяты для того, чтобы более точно построить график функции.

Следует заметить, что экстремумы функции f не всегда совпадают с наибольшим и наименьшим значением функции.

3.2 Признак возрастания и убывания функций

Если строить график функции по каким-либо произвольно выбранным его точкам, соединяя их плавной линией, то даже при очень большом числе случайно выбранных точек может оказаться, что построенный таким образом график будет сильно отличаться от графика заданной функции.

Если при исследовании функции использовать производную и найти так называемые «опорные» точки, т.е. точки разрыва, точки максимума и минимума, промежутки монотонности функции, то даже при небольшом числе таких «опорных» точек мы получим правильное представление о графике функции.

Определение монотонности функции на интервале Функция y = f(x) называется возрастающей на интервале, если для любых точек х1 и х2 этого интервала из условия

х1< х2 следует, что f(x1) < f(x2). Если же из условия х1 < х2 следует, что f(x1) > f(x2), то функция называется убывающей на этом интервале.

Достаточный признак монотонности функции в интервале. Теорема: если функция имеет положительную (отрицательную) производную в каждой точке интервала, то функция возрастает (убывает) на этом интервале.

Геометрическое истолкование теоремы весьма простое, если вспомнить, что f’(x) = tgα, α – это угловой коэффициент касательной к графику функции в заданной точке х. Если, например, f‘(x) > 0 во всех точках некоторого интервала, то касательная к графику с осью абсцисс образуют острые углы, а значит, с ростом х возрастает и f(x). Если же f‘(x) < 0, то касательная с осью абсцисс образуют тупой угол, а значит, с ростом х функция f(x) убывает. Поскольку эти рассуждения основаны лишь на наглядных геометрических представлениях, они не являются доказательством теоремы. 3.3. Критические точки функции, максимумы и минимумы.

Определение точек экстремума функции. Пусть х0 – внутренняя точка из области определения функции f(x). Тогда, если существует такая δ – окрестность ) x0- δ, x0+ δ ( точки х0, что для всех х из этой окрестности выполняется неравенство f(x) ≤ f(x0) (неравенство f(x) ≥ f(x0)), точка х0 называется точкой максимума (точкой минимума) этой функции.

Точки максимума минимума являются внутренними точками области определения функции.

Необходимый признак существования экстремума дифференцируемой функции.

3.3 Теорема Ферма

Если х0 есть точка экстремума функции f(x) и в этой точке производная существует, то она равна нулю: f ’(x0)=0.

Эта теорема не является достаточным условием существования экстремума дифференцируемой функции: если в некоторой точке х0 производная обращается в нуль, то из этого еще не следует, что в точке х0 функция имеет экстремум.

Замечание: теорема не верна, если функцию рассматривать на отрезке.

Определение критических точек функции. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называют критическими точками функции.

Достаточные условия существования экстремума.

Теорема 1. Если функция f(x) непрерывна в точке х0, f‘(x) > 0 на интервале (a, x0) и f‘(x) < 0 на интервале (x0, b), то х0 является точкой максимума функции f(x).

Теорема 2. Если функция f(x) непрерывна в точке х0, f‘(x) < 0 на интервале (a, x0) и f‘(x) > 0 на интервале (x0, b), то х0 является точкой минимума функции f(x).

Для отыскания экстремальных точек функции нужно найти ее критические точки и для каждой из них проверить выполнение достаточных условий экстремума.

3.4 Наибольшие и наименьшие значения функции

Правила отыскания наибольшего и наименьшего значений функций в промежутке. Для отыскания наибольшего и наименьшего значений функции, дифференцируемой в некотором промежутке, нужно найти все критические точки, лежащие внутри промежутка, вычислить значения функции в этих точках и на концах промежутка и из всех полученных таким образом значений функции выбрать наибольшее и наименьшее.

Сегодня математика выступает в качестве необходимого и вполне работоспособного инструмента, используемого для повышения эффективности результата в различных областях целенаправленной человеческой деятельности. Одной из таких областей является управление предприятиями и другими организациями, ведение современного хозяйства – менеджмент и экономика. Решение многих управленческих и экономических задач строится на рассмотрении зависимостей интересующих нас величин от различных факторов. Функция показывает, как одна величина зависит от другой. При этом ту величину, от которой ищется зависимость, называют независимой переменной или аргументом (х), а ту величину, которая зависит от аргумента, называют зависимой величиной или функцией (у). Например, можно сказать, что прибыль является функцией от затрат или что цена товара есть функция от спроса на него. Выражение функции в общем виде записывается как у=f(x) Например, известно, что рентабельность (норма прибыли - НРПР) связана с прибылью (ПР) следующим образом: НРПР = ПР : З ∙100%, где З – затраты. Здесь прибыль является аргументом, а норма прибыли – функцией прибыли. Важной для менеджмента и экономики является функция, показывающая зависимость эффективности (Э) от дохода (Д) и затрат: Э = Д : З. В математике различают следующие основные простейшие функции:

- постоянные: у = С, (C = const),

где С – постоянное число;

- степенные: у = уⁿ;

- показательные: у = ах Складывая, вычитая, умножая и деля простейшие функции, получают так называемые элементарные функции. Вот некоторые из часто употребляемых в менеджменте и экономике элементарных функций:

- линейная функция или линейная форма: y = kx+b;

- функция второй степени или квадратичная форма: y = ax2+bx+c;

- функция n-й степени или многочлен n-й степени, например, многочлен 4-й степени:

 у = 5х4 + 3х3 + 4х2 + 7х – 6.

4.1 Таблицы и графики

Функции обычно характеризуются математическими зависимостями, которые удобно представить в виде наглядных графиков. Следует иметь в виду, что по сложившейся традиционной практике в ряде экономических задач назначение координатных осей меняется: вертикальная ось используется для аргументов, а горизонтальная – для функций ( что иногда приводит к путанице). Особенно широкое применение получили графики функций прямой и обратной пропорциональности. Пример: Построить график нормы прибыли (рентабельности) в зависимости от прибыли при постоянных затратах, равных 750 у.д.е. Решение: Норма прибыли (рентабельность) рассчитывается по формуле: НРПР = ПР : З ∙ 100%. По этой формуле строится график нормы прибыли (функция) в зависимости от величины прибыли (аргумент) при постоянных затратах (примем З = 750 у.д.е.).

Пример: Построить график эффективности в зависимости от затрат при постоянном доходе, равном 100 у.д.е. Решение: Эффективность рассчитывается по формуле: Э = Д : З. По этой формуле строится график эффективности в зависимости от затрат при постоянном доходе (примем Д = 100 у.д.е.).

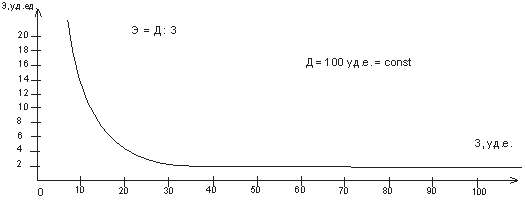
Это график обратной пропорциональности. В тех случаях, когда нет возможности представить функцию в виде математической формулы, построению графика предшествует составление таблицы, содержащей данные об интересующей нас зависимости. В этих таблицах значения аргументов и функций даются с интервалами, достаточными для построения плавного графика. Пример: Рассмотрим спрос на мороженое в ларьке за один день.

Решение: По данным таблицы построим график спроса. По традиции аргументы здесь откладываются по оси у, а функции – по оси х. График представляет собой кривую обратно пропорциональной зависимости, что соответствует закону спроса.

Анализируя таблицу и график, следует отличать спрос от величины спроса. Спрос в данном случае – это вся совокупность цен и соответствующего количества товара в таблице. На графике спросу соответствует вся кривая линия. Величина же спроса – это конкретное значение количества товара, продаваемого за один день по каждой данной цене; ей соответствуют отдельные точки линии спроса на графике. Когда говорят об изменении спроса на товар, имеют в виду смещение в ту или иную сторону всей кривой (или новые значения цен, соответствующих количеству продаваемого товара в таблице). С помощью графика спроса можно решить следующие задачи: 1) определить величины спроса – количество продаваемого товара при любых изменениях цены; 2) определить характер изменения спроса (больше, меньше, без изменений) при изменениях цен на товар и количества продаваемого по этим ценам товара. Изменение спроса (положения кривой и ее формы) зависит главным образом от изменений:

- вкусов покупателей (например, повышение интереса к экологически чистым продуктам);

- числа покупателей;

- дохода покупателей;

- цен на сопутствующие товары (например, повышение цен на источники электропитания для переносной радиоаппаратуры изменяет спрос на саму аппаратуру);

- покупательских ожиданий (например, если ожидается неурожай, спрос на сельхоз продукцию может повыситься).

4.2 Пример исследования функции в менеджменте и экономике

Совместное рассмотрение спроса и предложения. Равновесная цена.

Совместное рассмотрение спроса и предложения начнем с анализа данных таблицы, где представлены спрос и предложение на мороженое за один день.

Спрос и предложение мороженого

По данным таблицы построим математическую модель – график спроса и предложения на мороженое за один день.

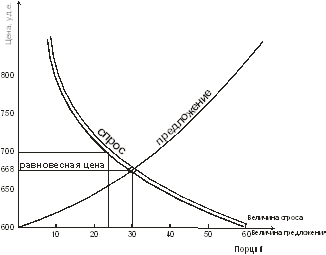
С помощью данной модели легко проследить динамику изменения спроса и предложения на товар и формирование его рыночной цены.

Цена, соответствующая точке на графике, находящейся в пересечении линии спроса и предложения, называется равновесной. В данном случае она равняется 668 у.д.е. Это та цена, по которой будет осуществляться купля-продажа товара при данных спросе и предложении, которые равны 30 порциям. Действительно, стоит продавцу поднять цену товара выше равновесной, например 700 у.д.е., как соответствующая ей величина спроса упадет до 25 порций. Но при этом до такой же величины должно будет упасть и предложение, что соответствует цене предлагаемого товара в 650 у.д.е. Уменьшение цены предлагаемого товара вызовет рост величины спроса, которая будет расти до тех пор, пока не приведет цену в равновесную точку: после равновесной точки дальнейший рост спроса будет ограничиваться падением цены и связанного с ним предложения. Таким образом, приход цены в равновесную точку осуществляется путем ее затухающих колебаний около равновесной точки. Тоже самое произойдет и при первоначальном установлении цены ниже равновесной точки – соответствующие изменения величин спроса и предложения возвратят цену в точку равновесия.

Заключение

Справедливости ради надо сказать, что по сравнению с другими науками экономика и менеджмент были на одном из последних мест по глубине проникновения в них математических знаний, созданию количественных методов исследования. Многие ученые-экономисты считали (а некоторые считают и по сей день), что экономика, управление организациями, как и другие общественные науки, - знания чисто описательного характера. Потребности практики, однако, требуют от экономики и менеджмента все более точных и изощренных расчетов. И тут без математики не обойтись. Развитие предпринимательства сопровождается появлением и быстрым совершенствованием науки о рыночном управлении предприятиями и производством – становлением научного менеджмента. Математика – язык, на котором сегодня говорит любая точная наука. Математические идеи пронизывают современные макро и микроэкономику, служат основой автоматизации управленческих и производственных процессов, базой для совершенствования компьютерных программ. В настоящее время математический аппарат является признанным инструментом менеджмента и экономики. С его помощью разрабатываются конкретные прикладные задачи управления предприятиями и организациями, оптимизации бизнеса и производства, финансового регулирования.

Список литературы

1. Башмаков, М.И. Алгебра и начало анализа.- М.: Просвещение, 1992.

2. Гусев, В.А. Математика: Справочные материалы.- М.: Просвещение, 1888.

3. Дорофеев, Г.В. Пособие по математике для поступающих в ВУЗы.- М.: Наука, 1974.

4. Зорин, В.В. Пособие по математике для поступающих в ВУЗы.- М.: Высшая школа, 1980.

5. Абчук В.А. Математика для менеджеров и экономистов: Учебник.-СПб.: Изд-во Михайлова В.А., 2002 г.

6. Исследование операций в экономике: Учеб. Пособие для вузов /Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман; Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2005г.