Скачать

Матемитические основы моделирование 3d объектов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ РОМАНО-ГЕРМАНСКИХ ЯЗЫКОВ

КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ В ОБУЧЕНИИ И

УПРАВЛЕНИИ УЧЕБНЫМ ПРОЦЕССОМ

«Допущена к защите»

Зав. кафедрой информационных

технологий в обучении и

управлении учебным процессом

доктор педагогических наук,

профессор, академик Академии

Информатизации Образования

«___»_________________2003г.

_____________Брановский Ю.С.

ДИПЛОМНАЯ РАБОТА

МАТЕМИТИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЕ 3D ОБЪЕКТОВ

Выполнила: студентка 5 курса

ФРГЯ отделения

«информатика/лингвистика и

межкультурная коммуникация»

Турлаевой Ольги Ивановны

Научные руководители:

кандидат тех. наук, доцент

кафедры ИТО и У Микула Н.П.

кандидат пед.наук,

доцент Диканская Н.Н.

Дата защиты___________2003 год

Оценка:______________

Ставрополь

2003г.

Содержание

Введение…………………………………………………………………….….….3

Глава 1 Компьютерное моделирование в базовом курсе информатики.….…..6

§1.Методологические основы моделирования………………………………….6

§2. Цели и задачи компьютерного моделирования……………………………13

§3. Теоретические аспекты математических основ моделирования, математическое моделирование, как научная методология решения проблемы…………………………………………………………………….......18Глава 2 . Роль компьютерного моделирования в процессе обучения……………………………………………………………………...…..25

§1. Общая классификация моделей…………………………………...………..27

§2. Разновидности материальных моделей, информационные модели …..…31

Глава 3.Методические рекомендации курса «Математические основы моделирования 3D объектов» базового курса «компьютерное моделирование» для студентов педагогических ВУЗов специальности преподаватель информатики……………………………………………………43

§1. Принципы построения электронного учебника……………………………………………………………………….…43

§2. Структура электронного учебника «Математические основы компьютерного моделирования 3D объектов»…………………………..…….56

§3. Методика проведения занятий с использованием электронного учебника……………………………………………………………………….....61

Заключение…………………………………………………………………….....63

Библиография…………………………………………………………………….65

Ведение

Современный период развития цивилизованного общества характеризует процесс информатизации, то есть переход от индустриального к информационному обществу. Информатизация общества – это глобальный социальный процесс, особенность которого состоит в том, что доминирующим видом деятельности в сфере общественного производства является сбор, накопление, продуцирование, обработка, хранение, передача и использование информации, осуществляемые на основе современных средств микропроцессорной и вычислительной техники, а также на базе разнообразных средств информационного обмена.

Одним из приоритетных направлений процесса информатизации современного общества является информатизация образования – внедрение средств новых информационных технологий в систему образования. Быстрый прогресс в области информационных технологий позволяет использовать персональные компьютеры в качестве эффективного средства обучения.

В этой связи важнейшей задачей высшего педагогического образования является подготовка учителей информационно грамотных, владеющих основами современных информационных технологий переработки информации, знающих современное состояние уровня и направлений развития вычислительной техники и программных средств, умеющих использовать компьютер и программные средства учебного назначения для решения своих профессиональных задач.

Компьютер может стать мощным учебным средством в руках преподавателя при целесообразном и методически обоснованном его применении, при этом необходимо учитывать особенности реального процесса обучения.

Описание целей обучения, процесса достижения целей, совокупности форм, методов, способов, приемов обучения, то есть создание методик и педагогических технологий, становится одной из актуальных задач современной практической педагогики.

Кроме того, согласно Государственному образовательному стандарту к профессионально значимым умениям и навыкам учителей информатики относится программирование. В этой связи стремительное развитие информационных технологий актуализирует для будущих учителей проблему изучения новых современных сред визуального программирования. Изучить особенности различных сред программирования, сравнить их возможности, сформировать целостное восприятие, позволяющее увидеть место и роль языка программирования, а также приобрести и закрепить навыки математического моделирования в рамках базового курса «компьютерное моделирование».

Таким образом, актуальность проблемы, обусловили выбор темы данной дипломной работы.

Объектом исследования является процесс обучения.

Предметом исследования данной дипломной работы являются методические особенности процесса обучения.

Цель дипломной работы заключается в рассмотрении методических особенностей изучения курса «сатематическое моделирование 3D объектов» с использованием электронного учебника.

Цель работа обусловила решение следующих задач:

- изучить и проанализировать педагогическую литературу по теме дипломной работы;

- изучить сущность и структуру педагогической технологии;

- проанализировать особенности процесса обучения с использованием компьютеров;

- обобщить требования к электронному учебнику как важнейшему компоненту педагогической технологии;

- разработать электронный учебник для изучения математических основ трехмерной графики.

Для решения поставленных задач использовались следующие методы и приемы: методы системного и логического анализа и метод обобщения опыта; теоретический обзор и анализ литературных источников; интерпретационные методы (структурный, функциональный, комплексный).

Практическая значимость данной дипломной работы заключается в возможности использования разработанного электронного учебника «Математические основы моделирования 3D объектов» в рамках базового курса «компьютерное моделирование» для студентов гуманитарных специальностей в области информатики и информационных технологий.

Цели и задачи дипломной работы определили ее структуру. Дипломная работа состоит из введения, трех глав, заключения и списка литературы. Во введении обосновывается выбор темы, устанавливается ее актуальность, формулируются цели, задачи и методы исследования и определяется практическая значимость. В первой главе раскрывается сущность понятия модели, приводится классификация моделей и способов моделирования, определяется роль компьютерного моделирования в жизни общества. Во второй главе раскрывается роль компьютерного моделирования в процессе обучения. В третьей главе обобщаются принципы построения электронных учебников, описывается технология частнопредметного уровня разработанная для студентов гуманитарных специальностей и приводится методика проведения занятия с использованием электронного учебника «Математические основы моделирования 3D объектов». В заключении подводятся итоги проделанной работы, даются рекомендации и намечаются перспективы дальнейшей работы по совершенствованию электронного учебника.

Общий объём дипломной работы составляет 70 страницы, библиографический список включает 61 источник. Работа содержит 7 рисунков и 5 схем.

Глава 1

Компьютерное моделирование в базовом курсе информатики

§1. Методологические основы моделирования

Научное исследование есть процесс познания определенной предметной области, объекта или явления с определенной целью.

Процесс исследования осуществляется субъектом и заключается в наблюдении свойств объектов и выполнении действий с целью выявления и оценки важных с точки зрения субъекта-исследователя закономерных отношений между показателями данных свойств (1,65).

Моделирование является одним из наиболее эффективных методов исследования. Оно заключается в построении и изучении специальных объектов (моделей), свойства которых подобны наиболее важным, с точки зрения исследователя, свойствам исследуемых объектов (оригиналов). В широком смысле моделирование представляет собой научную дисциплину, в которой изучаются методы построения и использования моделей для познания реального мира (72,70).

Всякая научная работа, как правило, основывается на исходных понятиях и определениях, позволяющих однозначно понимать язык, применяемый для изложения этой дисциплины. Моделирование, как научная дисциплина, также содержит ряд специальных понятий, которые составляют начало методологических основ этой науки. (Концептуальная часть науки).

Философскую концепцию моделирования составляют теория отражения и теория познания, а формально-методическую основу моделирования составляют теория подобия, теория эксперимента, математическая статистика, математическая логика и научные дисциплины, изучающие те предметные области, которые подлежат исследованию методами моделирования.

В данной главе рассмотрим основные положения науки о моделировании реально существующих объектов и объектов, подлежащих созданию в будущем. Моделирование этих объектов имеет общую философскую основу, но существенно отличается в части прикладных методов исследования.

Изучение методологических основ моделирования целесообразно начать с рассмотрения философских понятий теории отражения реальной действительности в сознании некоторого субъекта. Это должно обеспечить нам однозначное понимание положений излагаемых далее прикладных теорий. Приведем определения наиболее существенных для моделирования философских понятий. Некоторыми из них мы уже пользовались без определения.

Предметная область - это мысленно ограниченная область реальной действительности или область идеальных представлений, подлежащая описанию (моделированию) и исследованию. Предметная область состоит из объектов, различаемых по каким-либо признакам (свойствам) и находящихся в определенных отношениях между собой, или взаимодействующих каким-либо образом.

В нашем представлении объект - это все что мы различаем как нечто целое, реально существующее, или возникающее в нашем сознании и обладающее свойствами, значения которых позволяют нам однозначно распознавать это нечто. Объект, на котором сосредоточивается внимание субъекта с целью исследования, называется объектом исследования.

Объекты воспринимаются и различаются субъектами лишь постольку, поскольку они обладают характерными свойствами или способностями. "Свойство" и "способность" также являются весьма важными понятиями в рассуждениях человека.

Свойством называется характерная особенность объекта, которая может быть замечена и оценена субъектом, например, вес, цвет, длина, плотность и тому подобное. Для оценки исследуемого свойства объекта субъект устанавливает определенную меру называемую показателем свойства. Для каждого показателя определяется множество значений (уровней, или градаций меры свойства), которые присваиваются ему в результате оценивания свойства. Следовательно, свойство объекта является реальностью, а показатель - субъективной мерой этой реальности, если, конечно, речь идет о реальных объектах.

Показатели всеобщих свойств материальных объектов, таких как пространство и время называются основными показателями. Подавляющее большинство показателей других свойств выражаются через показатели этих основных свойств. Поэтому единицы измерения основных показателей служат основой для построения стандартной системы единиц измерения физических величин и называются основными единицами измерения.

Выражение показателя некоторого свойства через основные единицы измерения, принятые в определенной стандартной системе единиц (мер), называется размерностью данного показателя.

С точки зрения субъекта свойства делятся на внутренние (собственные) свойства объектов, показатели этих свойств называются параметрами, и внешние, представляющие собой свойства среды, связанные некоторыми отношениями с параметрами данного объекта. Показатели свойств внешней среды, влияющих на параметры исследуемого объекта, называются факторами.

Свойства объектов выявляются только при их взаимодействии, или при сопоставлении объектов друг с другом. Сопоставление (комбинация) значений показателей, наблюдаемых свойств определенных объектов называется отношением. Говорят, что отношение истинно, если оно подтверждается практическим экспериментом, или логическим выводом. Отношение считается ложным, если оно опровергается практической проверкой, или логическим выводом. Иначе отношение считается неопределенным. Понятия "истинно", "ложно", "неопределенно" являются логическими значениями любого отношения, результатами субъективной его оценки.

Отношение называется функциональным (функцией F), если оно представляет собой однозначное отображение множества X значений показателя некоторого свойства в множество Y значений показателя того же, или иного свойства. Формально это записывают как F:= X * Y, или как F(X)=Y, или F * X * Y, где “* ” декартово произведение множеств.

Взаимодействие объектов определяется по результатам изменения значений показателей наблюдаемых свойств этих объектов. Поэтому каждому действию, или взаимодействию, мы присваиваем определенный результат. Это может быть значение, или определенная комбинация значений, показателей свойств взаимодействующих объектов. Действия над значениями показателей свойств объектов, выполняемые по определенным правилам и приводящие к предполагаемому результату, называются операцией или процедурой (45,89).

Значения показателей свойств объектов обозначаются символами из некоторого заранее определенного множества А, называемого алфавитом.

Множество объектов, взаимосвязанных между собой определенными отношениями, и выполняющих определенную общую для них целевую функцию или имеющих общее предназначение, называется системой.

Система, состоящая из алфавита А, строго определенных множеств отношений (G), операций (Q) и предназначенная для символического описания объектов и систем определенного класса, называется формальной системой. Такие системы используются в качестве языков математического моделирования.

Способность, по нашему мнению, есть готовность объекта проявлять определенные свойства в определенных условиях. И наоборот, способность объекта вести себя определенным образом квалифицируется как его свойство. Например, забегая вперед, отметим, что одним из свойств сознания человека является способность применять ранее накопленные знания для решения возникающих логических проблем. Эта способность называется интеллектом.

Энергия является одним из свойств материи, в силу которого все материальные объекты совершают движение в пространстве и времени, находясь в энергетическом взаимодействии и пространственно-временном отношении.

Пространство и время также являются всеобщими свойствами материи. Многочисленные эксперименты подтверждают, что все материальные объекты существуют не иначе как в пространстве и во времени. Как известно, значения показателей пространства и времени входят в состав основных единиц измерения всех физических свойств объектов.

Так как все свойства объектов изменяются во времени, то любой набор значений показателей этих свойств относится к определенному значению показателя времени (к моменту времени). Это отношение называется состоянием объекта.

Значения показателей свойств меняются с течением времени. В результате этого происходит смена состояний объектов. Акт смены состояний объекта, отнесенный к определенному промежутку времени, называется событием, а последовательность взаимосвязанных событий, происходящих на некотором интервале времени, называется процессом.

Важным всеобщим свойством материи является способность материальных объектов сохранять вещественные и энергетические результаты (следы) взаимодействия материальных объектов. В философии эта способность называется отражением. Высшая форма отражения проявляется в биологических системах, как способность чувственного восприятия окружающей среды, сохранения результатов восприятия и использования их для управления своим поведением.

Часть материально-энергетической системы, предназначенная для восприятия и хранения результатов отражения, с целью воспроизведения и использования их в интересах системы в целом, называется памятью. Результаты отражения объектов внешнего мира и внутренних ощущений в памяти человека называются образами.

Как правило, чувственные органы человека воспринимают не полный образ наблюдаемого объекта, а только те его свойства, которые данный человек считает наиболее существенными по каким-то причинам. Человек способен присваивать образам символические имена из некоторого языка и связывать эти имена определенными логическими (мысленными) отношениями. Сформированная в памяти человека логическая система имен (идентификаторов образов) называется понятием.

С другой стороны, понятие можно определить и как некоторую языковую конструкцию, имеющую определенный смысл, т.е. образное содержание.

Система понятий и логических отношений между ними, отражающая какую-нибудь сторону реальной действительности, называется знаниями. Каждый субъект обладает памятью и механизмом целенаправленной манипуляции понятиями и знаниями. В целом эта система называется сознанием.

Процесс целенаправленной манипуляции знаниями в сознании субъекта называется мышлением.

Сознание субъекта присваивает каждому понятию, как и образу, символическое имя, определенное на языке, которым владеет данный субъект. Из имен понятий и образов формируется текст, представляющий собой знания субъекта о некоторой предметной области, закодированные на данном языке. Наглядная схема определений, связанных с понятием предметной области, представлена на рис 1.

Рис. 1. Схема определения понятия "знания о предметной области".

Таким образом, основным элементом любого знания является понятие, представленное на определенном языке. Понятие в процессе приобретения знаний и в процессе мышления субъекта имеет три значения:

• семантическое, отражающее значения свойств объектов, замечаемых субъектом;

• синтаксическое, связывающее понятия в выражения, предложения и тексты, имеющие определенный семантический смысл и поэтому представляющие знания субъекта о предметной области на определенном языке;

• символическое, представляющее понятия, как слова и формальные выражения, составленное из символов алфавита языка данного субъекта.

Выражения, предложения и фразы со своими значениями образуются при помощи грамматики языка, используемого субъектом для представления знаний.

Грамматика представляет собой систему правил, определяющих логические отношения между понятиями с учетом их семантических, синтаксических и символических значений.

Следовательно, приобретение знаний о предметной области есть процесс формирования в сознании субъекта понятий о существенных свойствах объектов предметной области и отношений между понятиями в виде текста, состоящего из выражений, предложений и фраз, обладающих соответствующими семантическими, синтаксическими, и символическими значениями.

Анализ данного процесса позволяет выяснить механизм мышления субъекта и факторы, влияющие на правдоподобие (достоверность) знаний субъекта о предметной области, а также найти способы построения правдоподобных моделей предметных областей.

Сущность процесса исследования заключается в отыскании достоверных ответов на поставленные вопросы. Общеизвестно, что какой вопрос, такой и ответ. Научные исследования предполагают отыскание ответов на корректно поставленные вопросы. В таких вопросах, как правило, требуется выбрать одно из возможных (альтернативных) решений некоторой проблемы (задачи) по определенным условиям.

Условие, по которому осуществляется выбор искомого решения, называется критерием. Как правило, критерий формулируется в виде некоторого отношения на множестве значений определенного показателя, который будем называть аргументом критерия.

§2. Цели и задачи компьютерного моделирования

Целью исследования обычно является определение значений параметров исследуемого объекта удовлетворяющих определенному критерию. Это означает, что в процессе исследования необходимо изменять значения параметров исследуемого объекта и таким образом измерять значения показателя, служащего аргументом критерия.

Процесс исследования заканчивается, когда исследователь находит совокупность значений параметров объекта, удовлетворяющую заданному критерию с заданной достоверностью. Проведение таких исследований называется экспериментом.

На практике такое экспериментирование с реальными объектами, как правило, обходится очень дорого, либо вообще не представляется возможным из-за нежелательных последствий эксперимента. Поэтому обычно в таких случаях для проведения научных экспериментов реальные объекты заменяются соответствующими им более простыми, безопасными и доступными объектами, свойства которых подобны свойствам исследуемых реальных объектов в определенной существенной части.

Объект, с целью изучения которого проводятся исследования, называется оригиналом, а объект, исследуемый вместо оригинала для изучения определенных свойств, называется моделью. В качестве моделей могут выбираться естественные объекты, обладающие свойствами, подобными соответствующим свойствам оригинала, или же создаваться специальные искусственные объекты с нужными свойствами.

Моделирование есть метод (или процесс) изучения свойств объектов-оригиналов посредством исследования соответствующих свойств их моделей.

Модели, представляющие собой материальные объекты, называются натурными или материальными.

При исследовании сложных систем, как правило, создать адекватную физическую модель не представляется возможным. В этих случаях ограничиваются созданием и исследованием математических описаний закономерных отношений между значениями параметров оригиналов. Такие описания называются математическими моделями.

Математическая модель - это образ исследуемого объекта, создаваемый в уме субъекта-исследователя с помощью определенных формальных (математических) систем с целью изучения (оценки) определенных свойств данного объекта.

Пусть некоторый объект Q обладает некоторым интересующим нас свойством C_0. Для получения математической модели, описывающей данное свойство необходимо:

1. Определить показатель данного свойства (т.е. определить меру свойства в некоторой системе измерения).

2. Установить перечень свойств С₁,...,С_m,, с которыми свойство С₀ связано некоторыми отношениями (это могут быть внутренние свойства объекта и свойства внешней среды, влияющие на объект).

3. Описать в избранной форматной системе свойства внешней среды, как внешние факторы х₁,...,х_n, влияющие на искомый показатель Y, внутренние свойства объекта, как параметры z₁,...,z_r, а неучтенные свойства отнести к группе неучитываемых факторов (w₁,...,w_s).

4. Выяснить, если это возможно, закономерные отношения между Y и всеми учитываемыми факторами и параметрами, и составить математическое описание (модель).

В обобщенном виде схема такого описания (моделирования) показана на рис. 2.

Рис. 2. Моделирование, как субъективное отражение

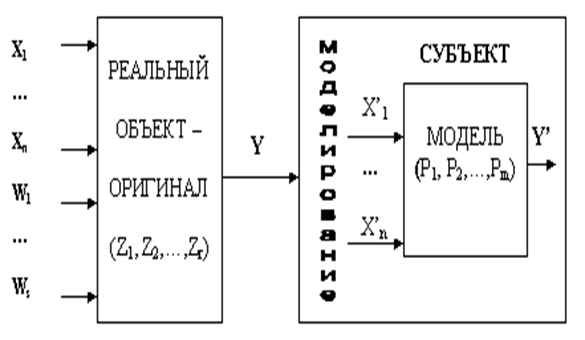
объективной реальности.

Как показано на этом рисунке реальный объект характеризуется следующим функциональным отношением между показателями его свойств:

Y=f(x₁,...,x_n,z₁,...,z_r,w₁,...,w_s). (1.1)

Однако в модели отображаются только те факторы и параметры оригинального объекта, которые имеют существенное значение для решения исследуемой проблемы. Кроме того, измерения существенных факторов и параметров практически всегда содержат ошибки, вызываемые неточностью измерительных приборов и незнанием некоторых факторов. В силу этого математическая модель является только приближенным описанием свойств изучаемого объекта. А математическую модель можно определить еще и как абстракцию изучаемой реальной сущности.

Модели обычно отличаются от оригиналов по природе своих внутренних параметров. Подобие заключается в адекватности реакции Y модели и оригинала на изменение внешних факторов x₁,...x_n. Поэтому в общем случае математическая модель представляет собой функцию

Y' = f(x'₁,...,x'_n,p₁,...,p_m), (1.2)

где p₁,...,p_m внутренние параметры модели, адекватные параметрам оригинала.

В зависимости от применяемых методов математического описания изучаемых объектов (процессов) математические модели бывают аналитические, имитационные, логические, графические, автоматные и т.д.

Главным вопросом математического моделирования является вопрос о том, как точно составленная математическая модель отражает отношения между учитываемыми факторами, параметрами и показателем Y оцениваемого свойства реального объекта, т.е. на сколько точно уравнение (1.2) соответствует уравнению (1.1).

Иногда уравнение (1.2) может быть получено сразу в явном виде, например, в виде системы дифференциальных уравнений, или в виде иных явных математических соотношений.

В более сложных случаях вид уравнения (1.2) неизвестен и задача исследователя состоит, прежде всего, в том, чтобы найти это уравнение. При этом к числу варьируемых параметров х'₁,...,х'_n, относят все учитываемые внешние факторы и параметры исследуемого объекта, а к числу искомых параметров относят внутренние параметры модели p₁,...,p_m, связывающие факторы х'₁,...,х'_n, с показателем Y' наиболее правдоподобным отношением. Решением этой проблемы занимается теория эксперимента. Суть этой теории состоит в том, чтобы, основываясь на выборочных измерениях значений параметров х'₁,...,х'_n, и показателя Y', найти параметры p₁,...,p_m, при которых функция (1.2) наиболее точно отражает реальную закономерность (1.1).

§3. Теоретические аспекты математических основ моделирования, математическое моделирование, как научная методология решения проблемы

Выше уже упоминалось о том, что математическая модель является не самоцелью, а только средством для решения определенной проблемы. В связи с этим необходимость создания математической модели вытекает из выбираемой исследователем методологии решения проблемы. Для решения сложных проблем обычно применяют так называемый системный поход, в котором моделирование является основным методом исследования. В целом системный подход предполагает следующие этапы решения проблемы (29,67):

* изучение предметной области (обследование),

* выявление и формулирование проблемы,

* математическая (формальная) постановка проблемы,

* натурное и/или математическое моделирование исследуемых объектов и процессов,

* статистическая обработка результатов моделирования,

* формулирование альтернативных решений,

* оценка альтернативных решений,

* формулирование выводов и предложений по решению проблемы.

В общем случае процесс исследования можно представить в виде следующей формальной системы:

(3.1)

Здесь X_(t) - множество значений входных факторов в момент времени t, О_(t) - множество значений параметров, характеризующих различные внутренние состояния сложной системы в этот же момент времени, Y_(t) и Y_(t-1) - множества значений измеряемых показателей изучаемых свойств системы в обозначенные моменты времени. Первые два уравнения моделируют суть изучаемого процесса, а третье уравнение является математическим описанием (моделью) процесса воздействий исследователя на изучаемую систему. Исследователю, как правило, доступно только определенное подмножество Y^’_(t) наблюдаемых параметров и весьма ограниченное подмножество X^’_(t) управляемых факторов. Его представление о внутренних состояниях исследуемой системы также ограничено некоторым подмножеством. Поэтому в представлении исследователя математическая модель исследуемой им системы имеет вид:

(3.2)

В целом формализованная схема процесса исследования сложной системы показана на рис. 3.

Рис. 3. Схема обобщенной математической модели процесса

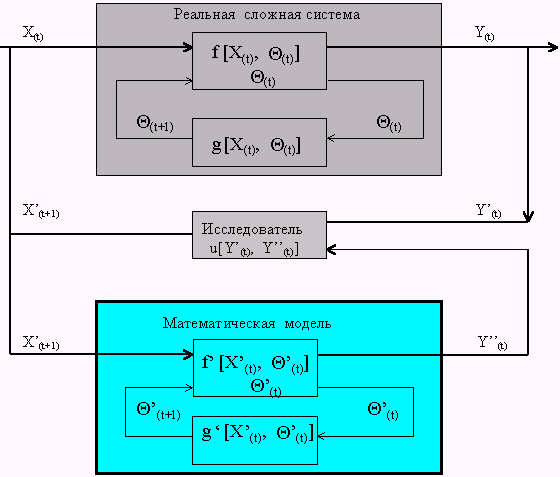
Таким образом, необходимость математического моделирования является основой системного подходак решению сложных проблем. Разработка математических моделей представляет собой сложную исследовательскую задачу, процесс решение которой состоит из следующих этапов:

* концептуальное проектирование,

* эскизное проектирование,

* техническое проектирование,

* рабочее проектирование,

* постановка и проведение модельного эксперимента,

* статистическая обработка результатов моделирования,

* формирование альтернативных решений исследуемой проблемы.

В зависимости от изучаемой предметной области, от решаемой проблемы, от математической подготовки исследователя и требований заказчика математические модели могут иметь различные формы и способы представления. В простейшем случае модель может представлять собой однофакторнуюлинейную или нелинейную функцию с постоянными числовыми коэффициентами (параметрами модели, отражающими внутренне состояние изучаемой системы). В этом случае показатель эффективности системы y’_(t) является однозначной неслучайной функцией от определенного фактора x’_(t). Примеромтакой модели является уже знакомая нам математическая модель электрического контура (рис 3). В данной модели исследуемым показателем является напряжение u_c на пластинах конденсатора C, а переменным внешним фактором - фактор времени t. Внутреннее состояние данного контура характеризуется значениями его параметров R, C и E. При этом изменение изучаемого показателя u_c(t) характеризуется дифференциальным уравнением: du_c(t)/d(t) = (u_c(t) - E )/ RC. Эксперимент с данной математической моделью сводится к решению данного дифференциального уравнения и к формулированию выводов о характере полученного решения. Для решения этой задачи применяется, как известно, метод наименьших квадратов. Классическим примером математической модели процессов такого типа является модель траектории полета космического аппарата, параметры которой уточняются по траекторным измерениям со станции наблюдения. Еще более сложным классом систем с точки зрения теории математического моделирования являются, так называемые, системы массового обслуживания. К ним относятся любые системы, в которых существует один или несколько потоков материальных или информационных объектов, которые обрабатываются определенным способом. Реальными системами массового обслуживания являются, например: телефонные станции, билетные кассы, информационно-вычислительные системы, автозаправочные станции и им подобные. К системам массового обслуживания космических средств относятся центры и пункты управления космическими аппаратами, системы сбора и передачи данных, стартовые комплексы и много других технических и организационных систем. При исследовании и моделировании систем массового обслуживания в качестве основных параметров, характеризующих функционирование этих систем, обычно рассматривают временные показатели: время наступления некоторого события - t_i, интервалы времени между событиями - l_i, интенсивность событий - m_i и соответствующие этим величинам распределения вероятностей*. Показателями эффективности функционирования систем массового обслуживания обычно являются:

1. для систем c отказами - среднее число отказов R(t₀, t) за время (t₀, t₀ + t), вероятность P(t₀, t) того, что за определенное время (t₀, t₀ + t) в системе не будет ни одного отказа,

2. для систем с ожиданиями обслуживания показателями эффективности также являются - среднее время ожидания заявки в очереди, среднее количество заявок в очереди, среднее время обслуживания одной заявки и тому подобные величины.

Способы математического моделирования систем массового обслуживания в настоящее время достаточно хорошо изучены и часто применяются на практике. Имеются аналитические формулы для оценки эффективности обслуживания в системах с простейшими (Пуассоновскими) потоками заявок. Они названы по имени их автора формулами Эрланга. Наконец, еще более сложными для исследования являются системы, функционирование которых представляет собой неоднородные разветвляющиеся процессы. К таким систем относятся, например: универсальные ЭВМ, центры и пункты управления различного назначения, сложные технические комплексы, в том числе и ракетно-космические. Эти системы имеют сложную внутреннюю структуру, состоящую из элементов (подсистем), выполняющих различные функции, подчиненные некоторой единой цели (целевой функции). Математическая модель сложной системы состоит из математических моделей ее подсистем и математической модели процесса взаимодействия между ними. Цели и задачи сложной системы достигаются в результате выполнения определенной композиции, состоящей из множества целевых функций ее подсистем, то есть:

F(S) = Ф(F₁(S₁), F₂(S₂), . . ., F_n(S_n)), (3.6)

где S - сложная система, S₁, ..., S_n - ее подсистемы, F₁, ..., F_n - цели функционирования соответствующих подсистем, Ф - математическое (формальное) описание закономерных связей между перечисленными целями.

Предполагается, что:

1. подсистема S_i сложной системы, как и вся система S в целом, функционирует во времени, и в каждый момент времени t она находится в одном из возможных состояний S_i(t);

2. с течением времени подсистема и система в целом под воздействием внешних и внутренних факторов переходят из одного состояния в другое;

3. в процессе функционирования системы (или подсистемы) она взаимодействует с внешней средой и другими системами, получая от них входной поток X(t) и выдавая выходной поток Y(t) событий, энергетических или материальных объектов.

Эффективность функционирования системы S, как правило, оценивается условной вероятностью достижения цели F(S) к заданному моменту времени. Целью функционирования системы S обычно является достижение определенного результата: обслуживание заданного количества заявок, поражение заданных объектов, решение заданных задач, производство определенного продукта и так далее. Существует несколько способов математической формализации таких процессов. К ним относятся: Марковские процессы, сети Петри, семантические сети, конечные автоматы и алгоритмы. Перечисленные математические формализмы хорошо изучены и достаточно полно изложены в литературе. Построение математических моделей сложных систем на основе типовых алгоритмических процессов является новым, мало известным, но весьма эффективным методом математического моделирования. Поэтому в дальнейшем основное внимание будет уделено этому методу. Описание алгоритмического процес