Скачать

Математическое моделирование процесса получения эмульгатора

Математическое моделирование технических объектов является одним из основных видов интеллектуальной деятельности учёного, исследователя, инженера. Моделирование предполагает построение моделей реально существующих объектов с целью:

1) раскрытия и углублённого исследования механизма явления и взаимодействия его частей;

2) установления технологических режимов, создания инженерных методов и расчётов;

3) определения конструктивных параметров машин и аппаратов;

4) оптимизации режима работы аппарата и оптимизации процесса;

5) создания средств автоматизации и систем управления.

Математической моделью называется приближённое описание какого-либо процесса или явления внешнего мира, выраженное с помощью математической символики.

Типовая модель процесса подбирается на основании имеющихся сведений об условиях проведения рассматриваемого процесса в аппарате выбранного типа.

При выборе модели необходимо учитывать следующее:

а) модель должна наиболее полно отражать характер потоков вещества и энергии при одновременно достаточно простом математическом описании;

б) параметры модели могут быть определены экспериментально или расчётным способом;

в) при гетерогенных системах модели выбираются для каждой из фаз, причём модели для обеих фаз могут быть одинаковыми или различными (например, для тарельчатого массообменного аппарата – идеальное вытеснение для паровой или газовой фазы и идеальное смешение для жидкой фазы);

г) применительно к процессам, происходящим в гомогенных системах, с достаточной для практики точностью может быть принята модель с сосредоточенными параметрами (основные переменные процесса изменяются только во времени); применительно к процессам, происходящим в гетерогенных системах, модель с сосредоточенными параметрами может быть принята для сплошной фазы, а модель с распределёнными параметрами (основные переменные процесса изменяются во времени и пространстве) – для дисперсной (в случае жидкой дисперсной фазы возможно применение модели с сосредоточенными параметрами для обеих фаз, поскольку можно допустить идеальное смешение в пределах каждой капли);

д) отдельное рассмотрение каждой фазы гетерогенной системы допустимо при скоростях, значительно более низких, чем скорости инверсии или захлёбывания; при достаточно больших скоростях фаз необходимо учитывать относительную скорость их движения или вводить фактор взаимодействия потоков. Следует принимать во внимание, что с изменением гидродинамического режима системы могут изменяться виды моделей (1).

Цель данной курсовой работы – создать математическую модель процесса получения эмульгатора (применяемого для стабилизации эмульсий «масло в воде») из масла и триэтаноламина и дать характеристику этой модели. Математическое моделирование данного процесса заключается в расчёте значений концентраций реагентов и величин потоков на выходе аппарата, в котором протекает реакция, и определении оптимального времени нахождения реагентов в реакторе.

1. Описание моделируемого процесса получения эмульгатора

Процесс получения эмульгатора описывается следующим уравнением химической реакции:

О

СН₂ – О – С

С₇Н₁₅ О

О СН – СН – ОН СН – СН – О – С 2 СН₂ – О – С  + 2 N - СН – СН – ОН =  С₇Н₁₅

С₇Н₁₅ СН – СН - ОН О

О 2 N - СН – СН – О – С + 3 C₂H₅OH

С₇Н₁₅

СН₂ – О – С О

С₇Н₁₅ СН – СН – О – С

С₇Н₁₅

Процесс ведут при температуре 120⁰С в цилиндрическом аппарате со сферическим дном и мешалкой при непрерывном и интенсивном перемешивании.

Если допустить, что, благодаря интенсивному перемешиванию, достигается однородность состава и температуры смеси во всём объёме реакционной зоны аппарата, то к данному процессу можно применить модель идеального смешения

Модель идеального смешения соответствует потоку через аппарат идеального смешения. Аппаратом идеального смешения называют такой аппарат, в котором поступающее в него вещество мгновенно распределяется по всему объёму аппарата. Концентрация вещества в любой точке аппарата равна концентрации на выходе из аппарата (2).

2. Вид модели

В широком смысле слова, модель – это любой образ (мысленный или предметный), замещающий рассматриваемый объект при его изучении. В зависимости от типа образа, замещающего моделируемый технологический объект, данная модель относится к абстрактным математическим моделям. Абстрактные модели основываются на описании технологического объекта на языке символов в той или иной области науки путём отвлечения от несуществующих признаков.

Процесс исследования технологического объекта с помощью абстрактных моделей включает три этапа:

1) построение описательной модели процесса или устройства;

2) запись информационной модели с помощью определённой системы символов;

3) исследование функционирования созданной абстрактной модели различными методами анализа.

По характеру отображаемых свойств данная абстрактная модель является функциональной. Функциональные математические модели предназначены для отображения физических и информационных процессов, протекающих в технологическом объекте при его функционировании. В общем случае они представляют собой системы уравнений, связывающие внутренние (характеризующие свойства отдельных переменных, их взаимосвязь и взаимодействие), выходные (получаемые при функционировании технического объекта) и внешние (характеризующие внешнюю среду, в которой происходит функционирование технического объекта) параметры объекта.

По характеру моделируемого процесса рассматриваемая модель относится к детерминированным, так как она позволяет, исключая влияние на процесс случайных характеристик, однозначно вычислить значения выходных величин по известным входным  параметрам.

По целям исследования описываемая модель является дескриптивной, т.е. описательной. Математическое моделирование реактора заключается в расчете значений концентраций реагентов и величин потоков на выходе аппарата и получение его статических характеристик.

По способу определения параметров модель является алгоритмической в силу того, что в её основе лежит составление эффективного алгоритма  для решения задачи при помощи компьютера.

Данную модель получают эмпирически, так для построения модели используются экспериментальные данные.

Так как в задаче рассматривается простейший химический процесс, то по принадлежности к иерархическому уровню описания объекта  модель относится к микроуровню  (типовые процессы – гидродинамические, теплофизические, массообменные, химические, биологические - обычно рассматриваются как нижний или элементарный уровень иерархии, неподлежащий дальнейшему разчленениею).

По порядку расчета описываемая модель является прямой. Её применение позволяет установить кинетические, статические и динамические закономерности процесса.

По классификации объектов математического моделирования, объекты данной модели являются объектами с высокой степенью информации. Их модели строят методами математического моделирования и реализуют на компьютерах, уточняя параметры по результатам испытаний реальных объектов.

Данная математическая модель описывает реальный процесс смешения масла и триэтаноламина с получением поверхностно-активного вещества – стабилизатора эмульсий при допущении, что, благодаря интенсивному перемешиванию, достигается однородность состава и температуры смеси во всём объёме реакционной зоны аппарата.

3. Математический аппарат моделирования, его алгоритм

Для получения уравнений математической модели синтеза эмульгатора рассмотрим реактор идеального смешения, в котором проводится реакция второго порядка:

О

СН₂ – О – С

С₇Н₁₅ О

О СН – СН – ОН СН – СН – О – С

2 СН₂ – О – С + 2 N  -  СН – СН – ОН  = С₇Н₁₅

С₇Н₁₅ СН – СН - ОН О

О 2  N - СН – СН – О – С + 3 C₂H₅OH

С₇Н₁₅

СН₂ – О – С О

С₇Н₁₅   СН – СН – О – С

С₇Н₁₅

Упрощённо её можно записать, как:

A+ВàС+D.

Требуется найти состав смеси на выходе, а также определить время, при котором концентрация вещества C будет иметь максимальное значение.

Идеализированная схема реактора идеального смешения для данной реакции представлена на рис.1. Условия физической реализуемости этой модели выполняются, если во всём потоке или на рассматриваемом его участке происходит полное (идеальное) смешение частиц потока. В таком случае любое изменение концентрации вещества на входе потока мгновенно распределяются по всему объёму аппарата.

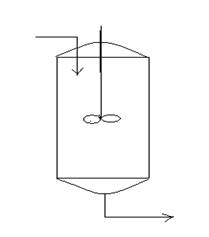
Са, Св, Сс, Сd

Рис.1 Идеализированная схема реактора идеального смешения

Са,о , Св,о – концентрация веществ А и В на входе в аппарат;

Са, Св, Сс, Сd – концентрации веществ А, В, С, D в определённый момент времени на выходе из аппарата.

Для каждого реагента запишем уравнение материального баланса движущегося потока, гидродинамическая структура которого близка к представлениям, связанным с идеальным смешением:

х *Ca,o - х * Ca + V * щ_a = 0

х * Cв,o - х * Cв + V *  щ_в = 0

х * Сс,о  + х * Сс + V * щ_с = 0 (1)

х * Сd,o  + х * Cd + V * щ_d=0

где х – объёмный расход реагента, м³/ч; Сi – концентрация реагента, кмоль/м³; щ_i- скорость химической реакции по i –му реагенту,  кмоль/( м³*ч).

Скорости образования реагентов описываются следующими кинетическими уравнениями:

щ_a = - 2*К* Са

щ_в = - 2*К* Св (2)

щ_с = 2*К* Сс

щ_d= 3*К * Сd

С учётом этого можно записать систему уравнений (1) иначе:

х * Ca,o - х * Ca – 2*V * K * Ca = 0

х * Cв,o  - х * Cв – 2*V * K * Cв = 0

х * Сс,о + х * Сс + 2*V * K * Сс = 0 (3)

х * Cd,o + х * Cd + 3*K * V * Cd = 0

С учётом  переменной ф = V/х, которая называется временем пребывания, можно упростить запись системы уравнений (3):

Ca,o - Ca -  2*ф * K * Ca = 0

Cв,o  - Cв -  2*ф* K * Cв = 0

Сс,о + Сс + 2*ф * K * Сс = 0 (4)

Сd,о + Cd + 3*ф * K * Cd = 0

Если записать систему уравнений (4) относительно определяемых переменных, то мы получим математическую модель описываемого процесса:

Ca = Ca,o  / 1 +2*K*ф

Cв = Cв,o  / 1 + 2*K*ф

Сс = Сс,о / 1 – 2*K*ф (5)

Cd = Cd,o / 1 – 3*K*ф

Степени превращения веществ А и В не могут превышать единицу и равны:

Ха = (Са,о – Са) / Са,о

Хв = (Св,о – Св) / Св,о

Функция Сc(ф) имеет максимум. Величину ф_опт, соответствующее максимальному значению концентрации Сс, можно найти аналитически.

Дифференцированием третьего уравнения системы (5) по ф находим оптимальные условия проведения реакции.

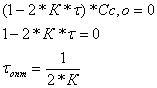 (6)

Таким образом, моделирование данного процесса сводится к расчёту концентраций на выходе из реактора по формулам (5). Максимальную концентрацию вещества С можно найти по аналитической формуле (6) или использовать численный метод поиска экстремума функции.

Алгоритм программы.

1. Задают начальные концентрации Са,о, Св,о константу скорости реакции K, объёмный расход реагентов х, объём аппарата V.

2. Находят время пребывания реагентов в реакторе ф = V/х и оптимальное время ф_опт.

3. Проверяют условие того, чтобы время пребывания реагентов в реакторе не было меньше ф_опт: ф > ф_опт. Если это условие выполняется, то переходят к пункту 7

4. Рассчитывают выходные значения концентраций Са, Св, Сс, Сd.

5. Проверяют условие того, что степени превращения веществ А и В не превышают единицы: Ха<1, Хв<1. Если оно выполняется, то  переходят к пункту 7.

6. Проводим расчет сначала.

7. Окончание расчёта, вывод результатов.

4. Выбор пакета моделирования

В настоящее время разработаны и используются разнообразные системы компьютерной математики (Matematika, MATLAB, Maple, MathCAD, Derive, MuPAD и др.).  Каждая из них имеет свои преимущества, недостатки и области применения.

Отличительной особенностью Mathcad является запись математических задач в форме максимально приближенной к записи их без применения компьютера. Эта система снабжена удобным пользовательским интерфейсом и обладает математическими возможностями для решения большинства инженерных задач.

Процесс создания программы в MathCAD идет параллельно с ее отладкой. Пользователь, введя в MathCAD-документ новое выражение, может сразу подсчитать, чему оно равно при определенных значениях переменных и построить график, а беглый взгляд на результаты может безошибочно показать, где кроется ошибка – в записи формул или в создании математической модели.

MathСAD – это полноценное Windows-приложение, поддерживающее передачу данных в среду другой программы. Документы, выполненные в MathCAD, отвечают всем типографским требованиям к текстовым документам.

Из графиков видно, что с увеличением времени пребывания концентрации исходных веществ уменьшаются, а продуктов – увеличиваются. Максимальный выход продуктов достигается при времени пребывания реагентов в реакторе ф = 6 секунд.

Выводы

В данной курсовой работе дана характеристика математической модели синтеза эмульгатора из масла и триэтаноламина, рассчитаны значения концентраций реагентов и величин потоков на выходе из аппарата и определено оптимальное время пребывания реагентов в реакторе.

Также приведён пример моделирования рассматриваемого процесса в пакете MathCAD (определены зависимости концентраций продуктов и исходных веществ от времени пребывания в реакторе и построены графики этих зависимостей). Из графиков видно, что с увеличением времени пребывания концентрации исходных веществ уменьшаются, а продуктов – увеличиваются.

Список использованных источников

1 Кафаров В.В. Моделирование химических процессов. М.: «Знание», 1968. 64 с.

2 Шестопалов В.В. Математические модели химико-технологических процессов и систем: Конспект лекций. Ч.1.М.: 1977. 48 с.

3 Аникин В.Л. Решение задач математического моделирования и оптимизации процессов химической технологии средствами MathCAD: Учебное пособие. Екатеринбург: УГТУ-УПИ, 2004. 122с.