Скачать

Математическая модель системы слежения РЛС

Содержание. 1

Введение. 3

1 Общая теория оптимального управления. 6

1.1 Допустимые управления. 6

1.2 Основные направления в теории оптимальных процессов. 11

1.2.1 Метод динамического программирования. 12

1.2.2 Принцип максимума. 13

1.3 Программное управление. 16

1.4 Постановка задачи и способы решения. 18

2 Система оптимального управления. 24

2.1 Математическое описание электромеханической системы.. 24

2.2 Идентификация авторегрессионно-регрессионной модели. 29

2.3 Формирование ограничений. 37

2.4 Формирование оптимальных траекторий. 42

2.5 Анализ решений. 50

2.6 Общая структура системы оптимального управления. 55

2.7 Полученные результаты.. 58

3 Практическая реализация. 63

3.1 Реализация оптимального управления в среде пакета matlab. 63

3.2 Выбор микроконтроллера. 64

4 Экономическое обоснование проекта. 66

4.1 Технико-экономическая характеристика. 66

4.2 Маркетинговая ориентация. 66

4.3 оценка научно-технической результативности и социальной эффективности НИР  68

4.4 Производственный план. 74

4.4.1 Расчёт затрат на разработку. 75

4.4.2 Затраты на создание опытного образца. 77

4.4.3 Затраты на эксплуатацию.. 79

4.4.4 Ценообразование. 79

Выводы.. 80

5 Безопасность и экологичность проекта. 81

5.1 Анализ опасных и вредных факторов. 82

5.2 Мероприятия по улучшению условий труда. 83

5.2.1 Помещения и их освещение. 83

5.2.2 Уровень шума и вибрация. 85

5.2.3 Параметры микроклимата. 86

5.2.4 Защита от электромагнитных и электростатических полей. 87

5.2.5 Электробезопасность. 90

5.2.6 Дисплейные терминалы и ПЭВМ в составе АРМ.. 91

5.2.7 Организация и оборудование рабочих мест с ВДТ и ПЭВМ.. 93

5.2.8 Требования к организации режима труда и отдыха при работе на АРМ.. 95

5.3 Устойчивость проекта к чрезвычайным ситуациям. 97

5.4 Экологичность проекта. 98

5.5 Выводы.. 99

Заключение. 100

Приложение. 101

Блок-схема файл-функции OPTIMUM_CONTR.. 101

Во многих областях техники и технологии приходится иметь дело со следующей задачей, которую можно трактовать как задачу «сопровождения цели». Причем, наблюдаемый процесс в некоторых случаях является детерминированным, т.е. полностью определенным, а в некоторых — не известным, но и в том и в другом случае в нем присутствует шум — случайная составляющая. Заданием для управляемого объекта служит движение другого объекта — задающего. Таким образом, задача слежения сводится к задаче перевода системы из начального состояния в наперед заданное состояние, которое определяется фазовым состоянием наблюдаемой системы.

В начальный момент времени t₀ объект находится в фазовом состоянии x₀; требуется выбрать такое управление u(t), которое переведет объект в заранее заданное конечное фазовое состояние x₁ (отличное от x₀). При этом нередко бывает, что начальное состояние x₀ заранее неизвестно.

Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.

Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы сейчас очень распространены в технике, их изучением занимается теория автоматического управления.

В общем случае на вход регулятора подаются фазовые координаты объекта. Регулятор конструируется так, что его выходная величина u, поданная на вход объекта, нужным образом управляет работой объекта (т. е., например, возвращает объект в рабочее состояние, если он почему-либо вышел из этого состояния).

Обычно требуется, чтобы переходный процесс (т. е. процесс перехода из начального фазового состояния x₀ в предписанное конечное состояние x₁) был в определенном смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. п. Такой «наилучший» переходный процесс называется оптимальным процессом.

Разумеется, желательно, чтобы регулятор не просто возвращал объект в рабочее состояние, а делал это наилучшим образом, например, в смысле быстродействия (т.е. возвращал объект в рабочее состояние за кратчайшее время). В связи с этим в теории автоматического управления рассматриваются весьма различные (по устройству и степени сложности) регуляторы. Рассмотрение регуляторов, которые применялись на практике и изучались в руководствах по автоматическому регулированию до возникновения теории оптимальных процессов, приводит к выводу, что уменьшение времени переходного процесса связано с усложнением конструкции регулятора; поэтому, усложняя конструкцию регулятора, можно лишь приближаться к «идеальному», «оптимальному» регулятору, который во всех случаях осуществляет переходный процесс за кратчайшее время.

Одной из важных заслуг теории оптимальных процессов является установление существования оптимальных регуляторов и создание математического аппарата, позволяющего рассчитывать такие регуляторы. Оптимальные регуляторы существенно отличаются от тех, которые до сих пор изучались в теории автоматического управления.

На данном уровне развития техники и технологии для такого рода управления в большинстве случаев используются стандартные регуляторы (например, ПИД-регуляторы). Во многих случаях их применение может быть оправдано и их работа удовлетворяет поставленным целям управления, но существуют ситуации, в которых применение таких регуляторов не дает необходимого результата. Использование ПИД-регуляторов может оказаться нецелесообразным в случае ограничений на управление. В такой ситуации, система в целом оказывается существенно нелинейной и классические приемы управления в этом случае не приемлемы.

В данной работе рассматривается система, состоящая из двух электроприводов, один из которых является ведущим, а другой — ведомым. Ведомый двигатель должен двигаться синхронно с ведущим. Система должна отрабатывать заданную траекторию с необходимой точностью и максимальным быстродействием.

1.1 Допустимые управления

Наиболее перспективным решением экстремальных задач является их решение на основе теории принципа максимума Понтрягина. В данной работе ставилась задача оптимизации по времени, для чего и были использованы методы оптимального управления, предложенные Л.С. Понтрягиным, В.Г. Болтянским, Р.В. Гамкрелидзе. (1)

Задача оптимального быстродействия заключается в отыскании такого управления u(t), для которого фазовая траектория x(t) проходит через точку x₁ и переход из х₀ в х₁ осуществляется за кратчайшее время. Такое управление u(t) называется оптимальным управлением (в смысле быстродействия); точно так же соответствующую траекторию x(t), по которой фазовая точка за кратчайшее время переходит из состояния x₀ в состояние x₁ называется оптимальной траекторией.

Обычно управляющие параметры u¹,...,u^r не могут принимать совершенно произвольные значения, а подчинены некоторым ограничениям. Это обусловлено техническими характеристиками реальных объектов управления, а также конструкцией регулирующих устройств.

Например, для двигателя постоянного тока (ДПТ), одним из управляющих параметров служит напряжение якоря; однако именно в силу конструктивных особенностей ДПТ этот параметр подчинен ограничениям указанного типа. Так, значение этого параметра не может принимать сколь угодно большое значение.

Для объекта, содержащего r управляющих параметров u¹, u², ...,u^r, в приложениях часто встречается случай, когда эти параметры могут произвольно меняться в следующих пределах:

Т. е. каждая из величин u¹, u², ...,u^r представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задается неравенствами

                                                                            (1.1)

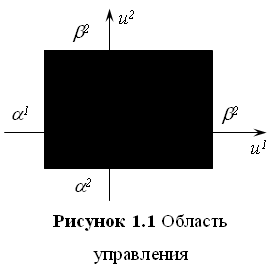
Заметим, что при r = 2 точки , координаты которых подчинены неравенствам (1.1), заполняют прямоугольник (рисунок 1.1); при r = 3 неравенства (1.1) определяют в пространстве переменных u¹, u², u³ прямоугольный параллелепипед.

В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано в пространстве переменных u¹, ...,u^r некоторое множество U и управляющие параметры u¹, u², ...,u^r должны в каждый момент времени принимать лишь такие значения, чтобы точка  принадлежала множеству U. Т. е. разрешается рассматривать лишь такие управления u(t), что  для любого t. Множество U называется областью управления.

Область управления U, в общем случае, может быть не только параллелепипедом, но может иметь более или менее геометрически сложный характер, так как благодаря конструкции объекта между управляющими параметрами могут существовать некоторые связи, выражаемые некоторыми уравнениями или неравенствами. Указанные области управления должны входить в математическое описание объекта.

Для технических задач важен случай замкнутого множества U, т.е. случай, когда точка  может находиться не только внутри множества, но и на его границе. Т.е. для «рулей» допустимы и их крайние положения.

Для полного осмысления данного вопроса необходимо сделать еще одно, очень важное, предположение о характере управлений. Возможны несколько случаев представления управляющих воздействий. А именно, в одном случае, когда это позволяет точность представления, можно предполагать, что «рули», положения которых характеризуются управляющими параметрами u¹, u², ...,u^r, безынерционны, так что есть возможность, если нужно, мгновенно переключать эти «рули» из одного положения в другое, т. е. менять скачком значения управляющих параметров u¹, u², ...,u^rв пределах области управления.

В другом случае, когда точность расчетов не допускает таких приближений нужно предполагать, что управляющие воздействия не могут меняться скачкообразно на сколь угодно большую величину, т.е. существует ограничение не только на значение управляющего параметра, но и на скорость изменения этого параметра. В этом случае достаточно написать , где  — скорость изменения управляющего параметра, и принять за управляющий параметр величину . Т. о. существует ограничение вида

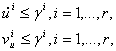                                                                                   (1.2)

что несколько осложняет поиск оптимального управления.

Всякий реальный процесс обладает некоторой «инерционностью», но во всяком реальном управляемом объекте всегда можно найти такие управляющие параметры, которые, в пределах заданной точности, можно считать безынерционными.

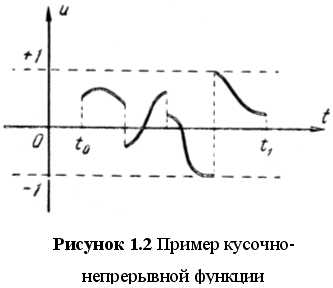
В соответствии с этим будут рассматриваться не только непрерывные, но и кусочно-непрерывные управления u(t). Класс кусочно-непрерывных управлений хорош тем, что, во-первых, позволяет получить точное математическое решение оптимальной задачи для широкого класса примеров, а во-вторых, наиболее интересен и удобен для технической реализации.

Необходимо уточнить, что функция со значениями в области управления U называется кусочно-непрерывной, если она состоит из конечного числа непрерывных кусков (рисунок 1.2), т.е. непрерывна для всех рассматриваемых t, за исключением лишь конечного числа моментов времени, где функция u(t) может терпеть разрывы первого рода; последнее означает, что в каждой точке разрыва t предполагается существование конечных пределов слева и справа:

Значение кусочно-непрерывного управления u(t) в точке разрыва не играет сколько-нибудь существенной роли. Однако для определенности будет удобно предполагать, что управление u(t) в точках разрыва непрерывно справа, т. е. что в каждой точке разрыва t значение управления u(t) равно пределу справа:

Кроме того, предполагается, что каждое рассматриваемое управление u(t) непрерывно в концах отрезка на котором оно задано, т. е. что все его точки разрыва, если они есть, расположены на интервале .

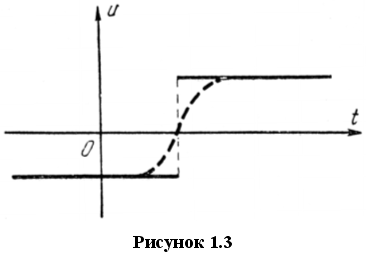
Допустимым управлением называют всякую кусочно-непрерывную функцию со значениями в области управления U, непрерывную справа в точках разрыва и непрерывную в концах отрезка  на котором она задана.

Оптимальные управления оказываются, в большинстве случаев, разрывными (т.е. содержащие скачки и переключения). Если разрывная функция, график которой изображен на рисунке 1.3 сплошной линией, представляет собой оптимальное управление, то, «сгладив» эту функцию (пунктир на рисунке 1.3), будет получена близкая к ней непрерывная функция. Но какая бы «близкая» к оптимальному управлению непрерывная функция ни была, всегда можно выбрать «сглаживающий» кусок еще более крутым и получить непрерывную функцию, еще более близкую к оптимальному управлению. Таким образом, в классе непрерывных функций просто не будет наилучшего, оптимального управления, а предельным случаем является кусочно-непрерывная функция, которая и является оптимальным управлением.

1.2 Основные направления в теории оптимальных процессов

Теория оптимальных процессов базируется на методе динамического программирования, разработанного Р. Беллманом, а также на принципе максимума Понтрягина. Для линейных систем принцип максимума был доказан Р.В. Гамкрелидзе. Кроме того, ему принадлежит теорема о конечности числа переключений. Доказательство принципа максимума для нелинейных систем принадлежит В.Г. Болтянскому.

Далее кратко рассмотрим общие принципы метода динамического программирования и принципа максимума.

1.2.1 Метод динамического программирования

Для получения уравнения Беллмана и формулировки теоремы, являющейся сущностью метода динамического программирования автором данной теории были выдвинуты следующие гипотезы.

Гипотеза 1.1. Какова бы ни была отличная от x₁ точка x фазового пространства, существует оптимальный (в смысле быстродействия) процесс перехода из точки x в точку x₁.

Время, в течение которого осуществляется оптимальный переход из точки x в точку x₁, обозначим через Т(х). И пусть

w(x) = — T(x).

Гипотеза 1.2. Функция w(x) непрерывна и всюду, кроме точки x₁, имеет непрерывные частные производные

На основе этих гипотез была сформулирована и доказана теорема 1.1.

Теорема 1.1. Если для управляемого объекта, описываемого уравнением , и предписанного конечного состояния x₁ выполнены гипотезы 1 и 2, то имеют место соотношения (1.3) и (1.4) (оптимальность понимается в смысле быстродействия).

 для всех точек x ¹ x₁ и u,

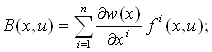                                                                (1.3)

для любого оптимального процесса (u(t), x(t)).                              (1.4)

Эта теорема и составляет сущность метода динамического программирования.

Метод динамического программирования (1.3), (1.4) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции w(x) так как эта функция входит в соотношения (1.3), (1.4). Во-вторых, уравнение Беллмана представляет собой уравнение в частных производных относительно функции w. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1.1 и 1.2. Ведь оптимальные управления и функция w заранее неизвестны, так что гипотезы 1.1 и 1.2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно.

Далее кратко излагается сущность принципа максимума, который является значительно более удобным средством для отыскания оптимальных процессов, чем метод динамического программирования.

1.2.2 Принцип максимума

Гипотеза 1.3. Функция w(x) имеет при x ¹ x₁ вторые непрерывные производные , а функции  — первые непрерывные производные .

Теорема 1.2. Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением

                                                                                  (1.5)

И предписанного конечного состояния x₁ выполнены гипотезы 1.1, 1.2 и 1.3. Пусть , — некоторый процесс, переводящий объект из начального состояния x₀ в состояние x₁. Введем в рассмотрение функцию H, зависящую от переменных  и некоторых вспомогательных переменных

........................................................................ (1.6)

С помощью этой функции H запишем следующую систему дифференциальных уравнений для вспомогательных переменных:

                                                            (1.7)

Тогда, если процесс  является оптимальным, то существует такое нетривиальное решение , системы (1.7), что для любого момента t, , выполнено условие максимума

                                               (1.8)

и условие

Эта теорема значительно удобнее для отыскания оптимальных процессов, чем метод динамического программирования. Однако в приведенной здесь форме принцип максимума страдает тем же недостатком, что и метод динамического программирования: он выведен в предположении дифференцируемости (и даже двукратной) функции w(x), а эта функция, как уже отмечалось, в действительности не является всюду дифференцируемой.

Однако принцип максимума доставляет достаточную информацию для решения поставленной задаче оптимального управления.

Благодаря работам Р.В. Гамкрелидзе, принцип максимума был доказан для линейных систем. Им были доказаны теоремы существования, единственности и теорема о числе переключений.

В данном случае функция Н принимает вид

                                                                               (1.9)

Выражение (1.7) в векторной форме записывается в виде

                                                                                      (1.10)

а соотношение (1.8) принимает в данном случае вид

                                                               (1.11)

Теорема 1.3 (теорема существования). Область управляемости является выпуклым открытым множеством фазового пространства Х; для любой точки х₀, принадлежащей области управляемости, существует оптимальное управление, переводящее точку х₀ в начало координат.

Примечание: Множество G называется открытым, если для каждой его точки можно найти шар с центром в этой точке, целиком принадлежащий множеству G, иначе говоря, множество G открыто, если к нему не причисляется ни одна точка его границы.

Областью управляемости объекта называется множество всех тех точек х₀ фазового пространства X, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат тоже причисляется к области управляемости.

Теорема 1.4 (теорема о числе переключений). Для каждого нетривиального решения y(t) уравнения (1.10) соотношение (1.11) однозначно определяет допустимое управление u(t); при этом оказывается, что функция u(t) кусочно-постоянна и ее значениями являются лишь вершины многогранника U.

Таким образом, функция u(t) кусочно-постоянна, принимает значения в вершинах многогранника U и определена однозначно. Каждую точку разрыва оптимального управления называют точкой переключения.

В общем случае число переключений хотя и конечно, но может быть произвольным. Однако существует один важный для приложений случай, когда число переключений допускает точную оценку. Этот случай рассматривается в теореме принадлежащей А.А. Фельдбауму. В этой теореме говорится (упрощенно), что каждая из функций  кусочно-постоянна и имеет не более —1 переключений (т.е. не более интервалов постоянства), где — порядок системы.

Таким образом, принцип максимума является наиболее удобным для решения задачи об оптимальном быстродействии.

1.3 Программное управление

Сегодня оборудование с программным управлением распространено весьма широко, начиная от компаний, входящих в TOP 500 Fortune в больших промышленных зонах, и заканчивая малыми предприятиями частного бизнеса. Действительно весьма трудно найти ту область машиностроения, где еще не используются уникальные возможности этого оборудования. Поэтому каждый специалист в области машиностроения должен хорошо представлять то, что дает производству применение этого весьма интеллектуального оборудования.

Программное управление технологическим оборудованием и процессами охватывает управление движением машин, механизмов, транспортных средств и изменением физических и химических параметров технологического процесса.

Программное управление — это управление режимом работы или состоянием объекта по заранее заданной программе. При автоматическом программном управлении технологическим оборудованием, соответствующая алгоритму программа записывается в память управляющего устройства с последующим автоматическим считыванием и преобразованием в управляющие сигналы.

Программное управление может быть реализовано на различных классах вычислительных машин, начиная от микроЭВМ и заканчивая мощными вычислительными системами. Каждый из этих классов накладывает на алгоритмы некоторые ограничения, которые необходимо учитывать при разработке алгоритмического обеспечения.

Разрабатываемый алгоритм ориентируется для использования в микроконтроллерах, что накладывает особые ограничения на полученный алгоритм.

Необходимо отметить, что микроконтроллеры выполняют операции для дискретного времени и дискретных величин. Вычисления осуществляются с конечной точностью и за конечное время.

Следует также учитывать тот факт, что микроконтроллеры не вычисляют точных значений интегралов и производных, но могут оценивать их значения в конечных разностях, т.е. с помощью численных методов.

Еще одним из важнейших условий, необходимым для успешной практической реализации, является необходимость учитывать отношение стоимости и мощности микроконтроллеров, которые будут использоваться в производстве.

Таким образом, после определения алгоритма оптимального управления для его реализации на реальном микроконтроллере необходимо выполнить оптимизацию по количеству операций, необходимых для проводимых вычислений, а также выполнить оценку точности вычислений. Оценка точности вычислений налагает ограничения на разрядность используемых микроконтроллеров, что в свою очередь сказывается на стоимости устройства в целом. Поэтому, изначально, алгоритм должен ориентироваться на элементарные операции сложения и вычитания, а также логические операции при переключении режимов.

При наличии сложных функциональных зависимостей, необходимо выполнить оценку их табулируемости для обеспечения высокого быстродействия работы алгоритма.

1.4 Постановка задачи и способы решения

В производстве всегда существовала проблема, сущность которой заключалась в переводе системы из некоторого начального фазового состояния в некоторое заранее заданное конечное состояние. Причем точность перехода должна быть максимальной, а время — минимальным.

В настоящее время эту проблему решает теория автоматического управления на базе стандартных регуляторов. Примером может служить широко распространенный ПИД-регулятор, на базе которого решается большой круг задач. Во многих случаях результаты, получаемы при использовании этих устройств, удовлетворяют потребностям управления. Там где не требуется очень высокое быстродействие или ограничения, накладываемые конструктивными особенностями и характеристиками реальных объектов на вид и характер переходного процесса не являются очень строгими возможно применять данные устройства.

Но с течением времени, в связи с развитием науки и техники инструменты производства все более усложняются, повышаются и требования к качеству управления. Под качеством понимается не только точность, но и быстродействие. Также возникают ситуации, в которых управление выработанное стандартными устройствами не может быть реализовано в полной мере из-за тех или иных технических характеристик объектов управления. Для удовлетворения современным запросам управления промышленные регуляторы совершенствуются и усложняются, что дает некоторый положительный результат, но приводит также и к нежелательным последствиям. А именно — с усложнением конструкции уменьшается надежность данного устройства и растет его стоимость, что, в свою очередь, тормозит внедрение его в производство.

Примером не адекватной работы устройств на базе стандартных регуляторов могут служить системы имеющие ограничения на управление. В такой ситуации, система в целом оказывается существенно нелинейной и классические приемы управления в этом случае не приемлемы и для достижения положительных результатов необходимо применять принципиально новые теории и законы, на базе которых можно получить такой вид регуляторов, который удовлетворял бы всем поставленным условиям и требованиям.

Целью данной работы является создание математической модели устройства, позволяющего адекватно управлять объектом при наличии ограничений на управление, причем главным условием ставится минимизация времени переходного процесса системы. Предполагается, что наиболее успешным и перспективным решением такого рода задач будет решение на базе теории принципа максимума Понтрягина.

В данной работе рассматривается радиолокационная установка, которая представляет собой совокупность как минимум двух синхронно вращающихся антенн, приводимых в движение электроприводами. В данной системе существует ведущий электропривод, который задает параметры вращения, и ведомый, который должен в точности повторять траекторию движения ведущего.

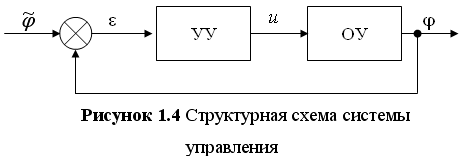
Предполагается, что тип двигателей, приводящих в движение эти антенны, не имеет для данной работы особого смысла. Сделаем следующее допущения: в данной системе есть возможность измерять в каждые заданные моменты времени положение ведущей антенны, т.е. есть возможность получать информацию о траектории ведущей антенны. Таким образом в связи со сделанными допущениями, система представляет собой совокупность двух электроприводов.

Ставится следующая задача: ведомый двигатель должен двигаться синхронно с ведущим. Система должна отрабатывать заданную траекторию с необходимой точностью и максимальным быстродействием.

В начальный момент времени оба двигателя могут быть рассинхронизированы. Конкретизируем задачу: необходимо за минимальный промежуток времени вывести ведомый двигатель на траекторию ведущего, причем в конце переходного процесса должны совпадать не только угол j, но также и скорость w, т. е., другими словами, ведомый двигатель попав на нужную траекторию, должен находиться на ней. Главным условием ставится минимизация времени переходного процесса. Таким образом ставится задача оптимально быстродействия.

Достижение указанной цели обусловлено решением следующих задач:

1. Построение оптимального программного управления системы слежения РЛС;

1.1. Построение оптимизационного функционала;

1.2. Вычисление точек переключения;

1.3. Нахождение оптимальных траекторий;

2. Моделирование полученной системы управления;

3. Проверка сделанных гипотез.

Предполагается, что процесс управления будет иметь циклический характер, так как в результате одного шага управления координаты ведущего и ведомого двигателей будут совпадать с некоторой погрешностью, которая в свою очередь будет являться начальными данными для следующего шага управления и т.д.

Запишем поставленную цель управления в виде:

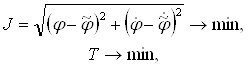                                                        (1.12)

где — J, T — целевые функционалы по ошибке и времени;  — выходные координаты ведомого двигателя;  — выходные координаты ведущего двигателя.

Выходные координаты ведущего двигателя в данном случае являются заданием.

Как было сказано выше, в реальных системах всегда существуют ограничения на управление, обусловленные техническими особенностями реальных объектов. В данном случае — это ограничение на напряжение якоря двигателя. Эти условия представляют собой ограничения на величину и на скорость изменения управляющего параметра U. Таким образом эти ограничения выделяют в пространстве управлений некоторое подпространство, называемое, как было сказано выше, областью управления. Область управления представляет собой r-мерный параллелепипед.

В теории принципа максимума было доказано, что управление будет оптимальным в случае движения по граням параллелепипеда области управления. В нашем случае областью управления является прямоугольник, так как множество управлений представляет собой пространство R². Управление будет представлять собой кусочно-непрерывную функцию.

Движение системы в фазовом пространстве должно проходить по оптимальным траекториям. Оптимальной траектория будет лишь в случае приложения оптимального управления, характер которого описан выше.

Для отыскания оптимального перехода в смысле быстродействия необходимо получить множество оптимальных траекторий. Это множество является общим решением системы уравнений, описывающих объект, при приложенном оптимальном управлении. Вид этих кривых будет описан ниже в главе 2.

Будем решать задачу в базисе ошибок.

Задавшись выражением (1.13)

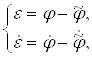                                                                                       (1.13)

где  — выходные координаты ведомой системы,  — выходные координаты ведущей системы, являющиеся заданием,  — ошибка и скорость ошибки, можно сформулировать задачу в базисе ошибки: за минимальный промежуток времени вывести ошибку e и ее производную  в нуль.

Так как оптимальное управление имеет вид кусочно-непрерывной функции имеющей точки переключения, то движение системы в базисе ошибок будет проходить по кривым, имеющим конечное число точек переключения (а соответственно и интервалов постоянства), соответствующим точкам переключения управляющего параметра. Таким образом возникает проблема нахождения моментов времени, в которые необходимо изменить значение (переключить) управляющего параметра.

Таким образом общая задача сводится к нахождению области управления, нахождению вида оптимальных траекторий и вычисление моментов времени точек переключения управляющего параметра.

В результате решения общей задачи, сформулированной выше, должен быть получен общий алгоритм функционирования системы оптимального управления, который необходимо оптимизировать для использования в микроконтроллерах.

2.1 Математическое описание электромеханической системы

В данной работе рассматривается радиолокационная установка, которая представляет собой совокупность как минимум двух синхронно вращающихся антенн. В данной системе одна из антенн является ведущей — она задает параметры движения, другая — ведомая, которая должна в точности повторять траекторию движения ведущей.

Каждая из антенн представляет собой сложную электромеханическую систему, представляющую собой совокупность таких составных частей как электропривод, редуктор и собственно принимающая антенна. Основным источником механической энергии является электропривод. Редуктор служит для преобразования угловых скоростей и соответственно вращающих моментов, выдаваемых двигателем. Редукторы могут быть зубчатые (в том числе червячные) или гидравлические.

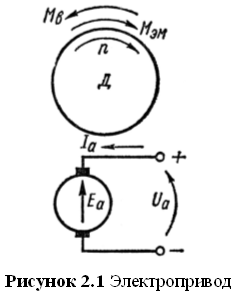
Напомним, что в разделе 1.5 были сделаны следующие допущения: в данной системе есть возможность измерять в каждые заданные моменты времени положение ведущей антенны, т.е. есть возможность получать информацию о траектории ведущей антенны; тип двигателя, приводящего в движение антенны является не существенным для данной работы.

Применяемые в настоящее время регулируемые и следящие электроприводы (ЭП) построены, в основном, с применением принципов подчиненного регулирования координат. В качестве координат выступают ток якоря двигателя, его скорость вращения и угол поворота вала двигателя (перемещение исполнительного органа рабочей машины).

Для решения поставленных в разделе 1.5 задач нет необходимости приводить полное точное математическое описание данной электромеханической системы. Так как нашей целью является не описание процессов, протекающих внутри этой системы, а регулирование поведения данной системы в целом. К тому же