Кручение стержней
Глава 1. Кручение стержней имеющих в сечении правильный многоугольник
§1.1 Кручение призматических стержней
§1.2 Кручение стержней прямоугольного сечения
§1.3 Мембранная аналогия
§1.4 Кручение тонкостенных стержней открытого профиля
Глава 2. Кручение стержней имеющих в сечении круг и эллипс
§2.1 Кручение стержней круглого и эллиптического сечений
§2.2 Кручение тонкостенных труб
§2.3 Кручение круглых валов переменного диаметра
Глава 3. Кручение призматических и цилиндрических стержней
§3.1 Чистое кручение стержней постоянного сечения
§3.2 Чистое кручение круглых стержней (валов) переменного сечения
Глава 4. Задачи
Заключение
Литература
ВВЕДЕНИЕ
Данная выпускная квалификационная работа состоит из четырех глав. В первой главе излагается прямой, обратный и полуобратный методы, применяемые при решении задач о кручении стержня прямоугольного сечения. Исследованы приближенные методы решения задач о кручении более сложных сечений.
Вторая глава посвящена изучению кручения стержней в сечении имеющих форму круга или эллипса. Применяют метод перехода к полярным координатам.
В третьей главе исследуется кручение призматических и цилиндрических стержней, исследуются общие построения данной теории и их различия.
В четвертой главе изучают теоретическое применение к решению задач.
Глава 1. КРУЧЕНИЕ СТЕРЖНЕЙ, ИМЕЮЩИХ В СЕЧЕНИИ ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК
§1.1 Кручение призматических стержней
Прямой метод решения задач теории упругости, заключающийся в интегрировании основных уравнений теории упругости совместно с заданными граничными условиями, не всегда возможен. Для многих задач удобно применять так называемые обратный и полуобратный методы. При пользовании обратным методом выясняют, каким граничным условиям соответствуют некоторые функции, удовлетворяющие дифференциальным уравнениям. Таким путем можно получить ряд полезных результатов. Полуобратный метод, впервые предложенный Сен-Венаном, состоит в том, что делают некоторые допущения в отношении напряжений или перемещений. При этом дифференциальные уравнения настолько упрощаются, что решение их не представляет особых математических трудностей. Принимая те или иные допущения, мы, как правило, ограничиваем общность полученного решения; но обычно их можно формулировать таким образом, чтобы все же получить решение частных задач. Например, в рассматриваемой ниже задаче о кручении призматического стержня мы будем задаваться определенными функциями для перемещений и, v, w, сводя, таким образом, основные уравнения к одному дифференциальному уравнению. Но при таких допущениях мы можем найти решение задачи о кручении стержней только постоянного сечения; решения же для стержней, не являющихся призматическими, получить этим путем нельзя. Полуобратный метод является одним из самых эффективных методов решения задач теории упругости.
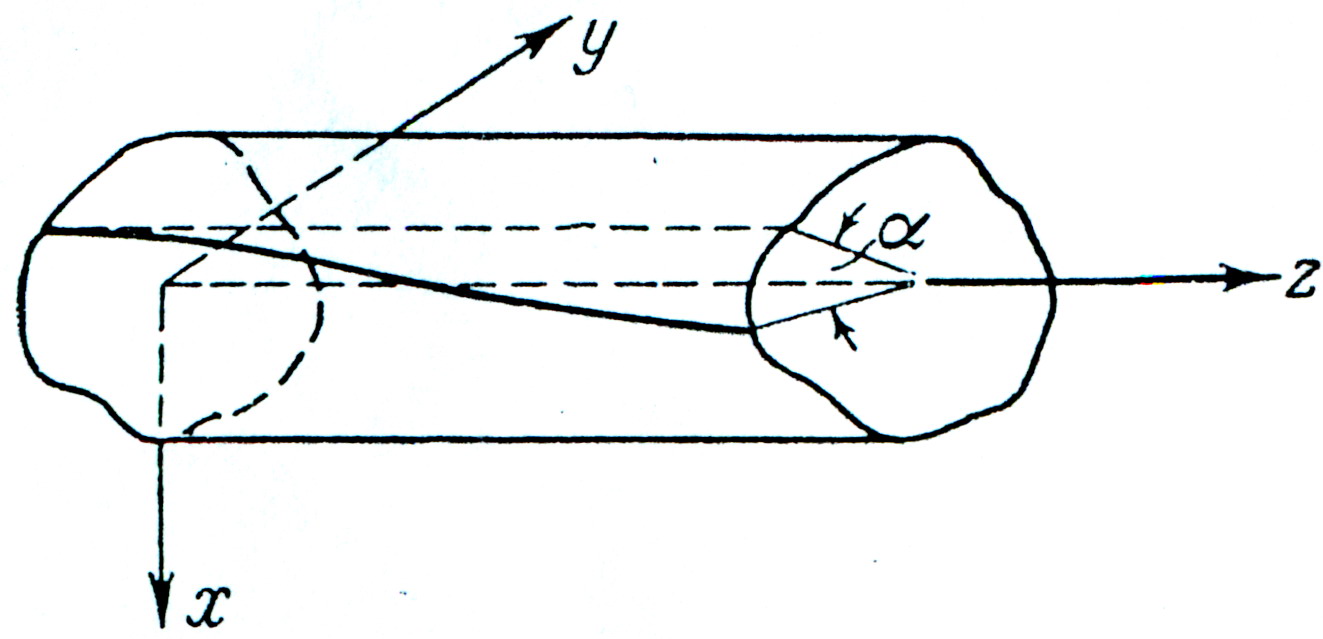
рис. 1
Предположим, что один конец стержня призматического сечения, длины L, закреплен в плоскости ху, а на другой конец действует пара, вектор-момент который направлен вдоль оси z (рис. 1). Мы полагаем, что закрепленный конец не может вращаться, но что оба конца могут свободно перемещаться друг относительно друга в направлении z. Под действием пары стержень будет закручиваться, причем образующие цилиндра будут превращаться в винтовые линии. Угол поворота любого поперечного сечения зависит от расстояния, на котором находится это сечение от закрепленного конца. При малой деформации можно считать, что угол закручивания ![]() пропорционален расстоянию между сечением и закрепленным концом. Таким образом,
пропорционален расстоянию между сечением и закрепленным концом. Таким образом,
![]() z, (1)
z, (1)
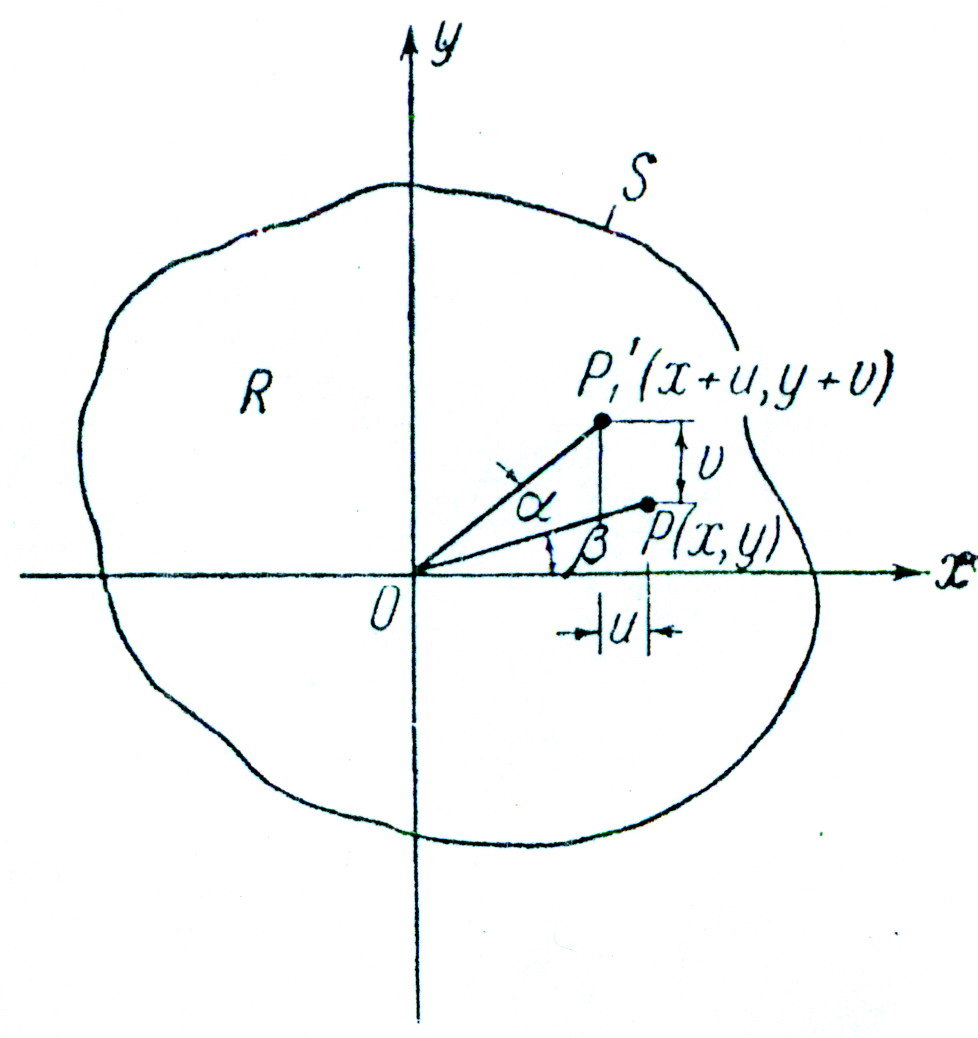
рис. 2
где ![]() угол закручивания на единицу длины. Будем считать угол закручивания
угол закручивания на единицу длины. Будем считать угол закручивания ![]() малым. Рассмотрим сечение стержня, которое находится на расстоянии z от закрепленного конца. Точка Р с координатами x, y, z в результате деформации перемещается в точку Р’(x+u, y+v, z+w). На рисунке 2 показана точка Р’1, являющаяся проекцией Р’ на плоскость xy.
малым. Рассмотрим сечение стержня, которое находится на расстоянии z от закрепленного конца. Точка Р с координатами x, y, z в результате деформации перемещается в точку Р’(x+u, y+v, z+w). На рисунке 2 показана точка Р’1, являющаяся проекцией Р’ на плоскость xy.
Предположим, что в плоскости xy точка Р перемещается в Р’1 при повороте на угол закручивания ![]() , причем ОР
, причем ОР![]() ОР’1= r. Если угол
ОР’1= r. Если угол ![]() мал, то cos
мал, то cos![]()
![]() 1 и sin
1 и sin![]() . Следовательно,
. Следовательно,![]()
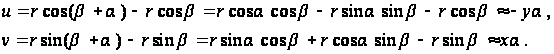
Подставляя значение ![]() (1), получаем
(1), получаем
![]() (2)
(2)
таким оказывается закон изменения u и v. В отношении w не будем пока делать никаких допущений, кроме того, что w зависит только от x и y и не зависит от z . Следовательно, можно записать
![]() (3)
(3)
где ![]() - некоторая функция от x и y .Так как w определяет искажение (депланацию) торцевых сечений, то функцию
- некоторая функция от x и y .Так как w определяет искажение (депланацию) торцевых сечений, то функцию ![]() можно назвать функцией депланацией. Необходимо выяснить, будут ли отвечать принятые выражения для перемещений, вместе с неизвестной еще функцией
можно назвать функцией депланацией. Необходимо выяснить, будут ли отвечать принятые выражения для перемещений, вместе с неизвестной еще функцией ![]() , напряженному состоянию, удовлетворяющему заданным граничным условиям. Эти условия в данном случае состоят в том, что на обоих торцах должны действовать, только крутящие моменты и что боковая поверхность стержня свободна от сил.
, напряженному состоянию, удовлетворяющему заданным граничным условиям. Эти условия в данном случае состоят в том, что на обоих торцах должны действовать, только крутящие моменты и что боковая поверхность стержня свободна от сил.
Пользуясь приведенными выше выражениями для перемещений, находим:
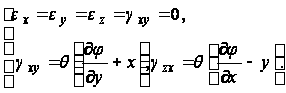 (4)
(4)
Из закона Гука следует:
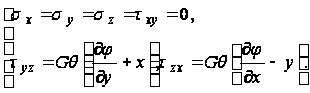 (5)
(5)
Подставим эти значения в уравнения равновесия, которые будут выполняться, в случае, если функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
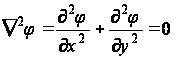
для всех точек поперечного сечения R стержня, здесь
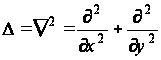
- оператор Лапласа.
Обратимся к граничным условиям. Так как
![]()
на боковой поверхности стержня, то уравнений примет следующий вид:
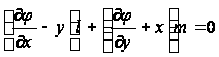 на контуре S,
на контуре S,
где S - контурная линия поперечного сечения стержня.
Покажем, далее, что на двух других граничных поверхностях, а именно, на торцах стержня, определяемых плоскостями z=0 и z=L, напряжение (5) сводятся к скручивающей паре, и результирующие силы отсутствуют. Результирующая сила в направлении x равна
![]()
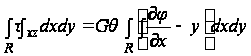 ; (8)
; (8)
это выражение можно привести к виду
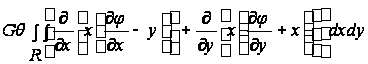 . (9)
. (9)
При получении уравнения (9) были использованы соотношения
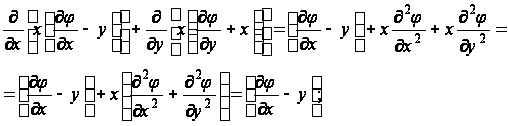
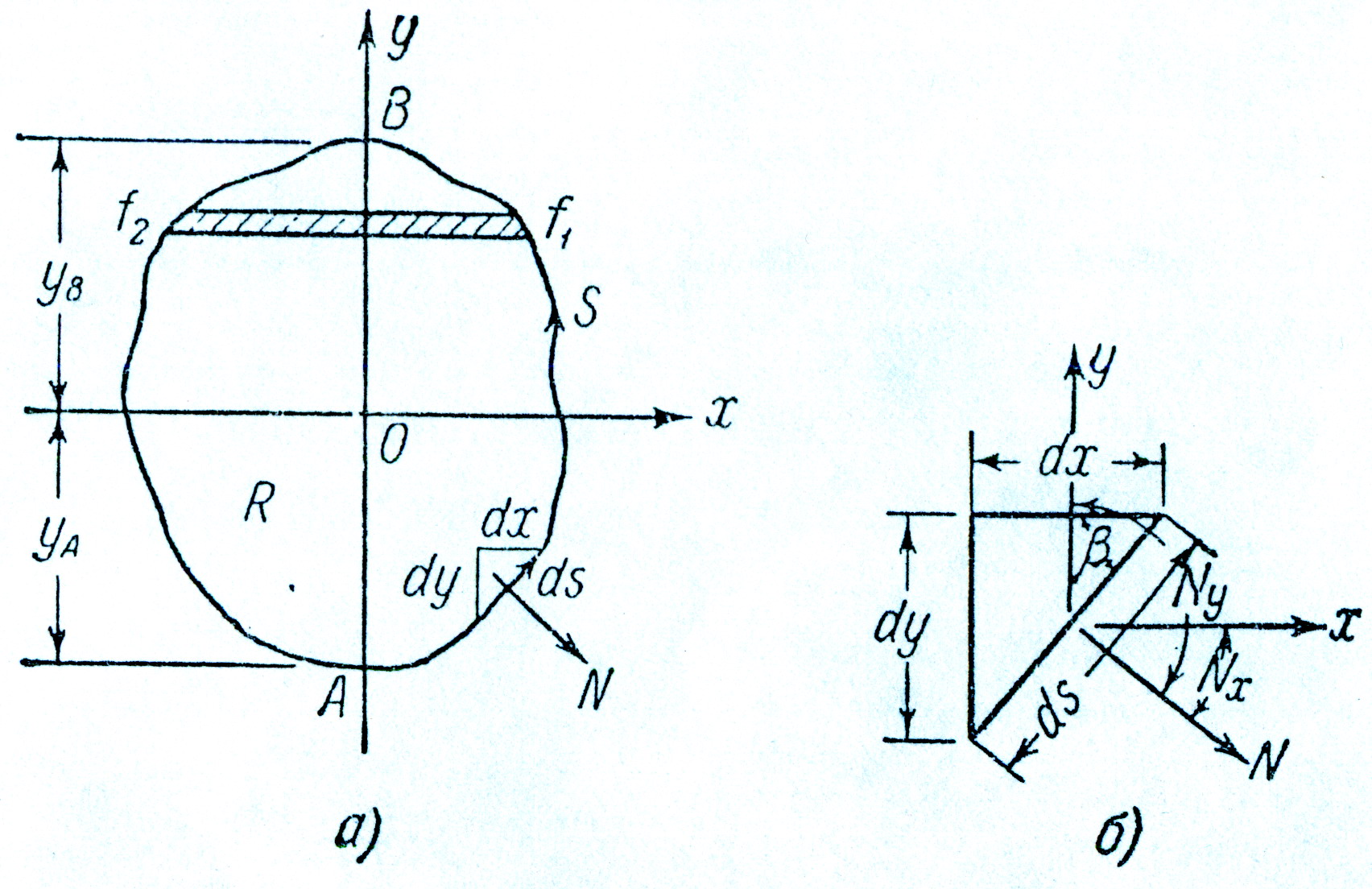
рис. 3
здесь принято
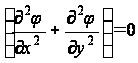
в соответствии с уравнением (6).
Пусть f является некоторой функцией x и y; тогда можно выписать равенства (рис. 3):
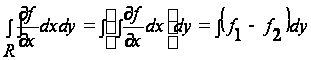
где f1 и f2 - значение функции f на правой и левой частях контура. Выполним интегрирование по y для контурной кривой в границах от y=yA до y=yB. Если мы будем вести интегрирование функции f по контуру в направлении против часовой стрелки, то для правой части контура приращение dy - положительно, а для левой - отрицательно. В результате каждая из величин f1dy и (- f2dy) окажется положительной, и, следовательно,
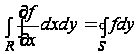 . (10)
. (10)
Аналогично,
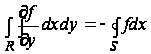 (11)
(11)
Пользуясь формулами (10) и (11), придадим выражению (9) вид:
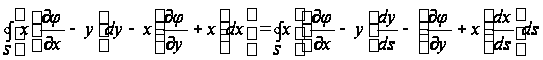 . (12)
. (12)
Будем считать положительными направления вдоль нормали N во внешнюю сторону и вдоль контура – против часовой стрелки; тогда согласно рис.3,б получим
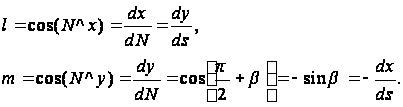 (13)
(13)
Равенство (12) принимает вид
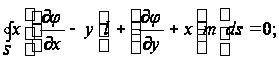
при этом выражение
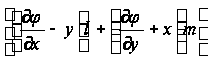
обращается в нуль на контуре S в соответствии с уравнением (7). Мы пришли, таким образом, к равенству
![]()
Таким же путем можно показать, что составляющая результирующей силы вдоль оси также равна нулю:
![]()
Следовательно, результирующие силы по торцам цилиндра обращаются в нуль.
Результирующий крутящий момент T по торцам стержня, отвечающий принятому распределению напряжений, равен:
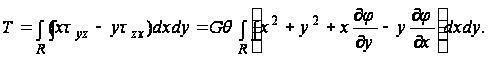 (14)
(14)
Интеграл, фигурирующий в выражении (14), зависит от функции кручения ![]() и, следовательно, от вида поперечного сечения R стержня. Вводя обозначение
и, следовательно, от вида поперечного сечения R стержня. Вводя обозначение
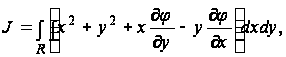 (15)
(15)
Получим
![]() (16)
(16)
где J – постоянная кручения. Уравнение (16) показывает, что крутящий момент пропорционален углу закручивания на единицу длины, так что произведение является мерой жесткости стержня, подвергаемого кручению; величина эта называется крутильной жесткостью стержня.
§1.2 Кручение стержней прямоугольного сечения
Пусть поперечное сечение стержня представляет собой прямоугольник с центром в начале координат и со сторонами 2a и 2b, направленными параллельно координатным осям, как показано на рис.7. Пользуемся полученными ранее уравнениями: для всей прямоугольной области
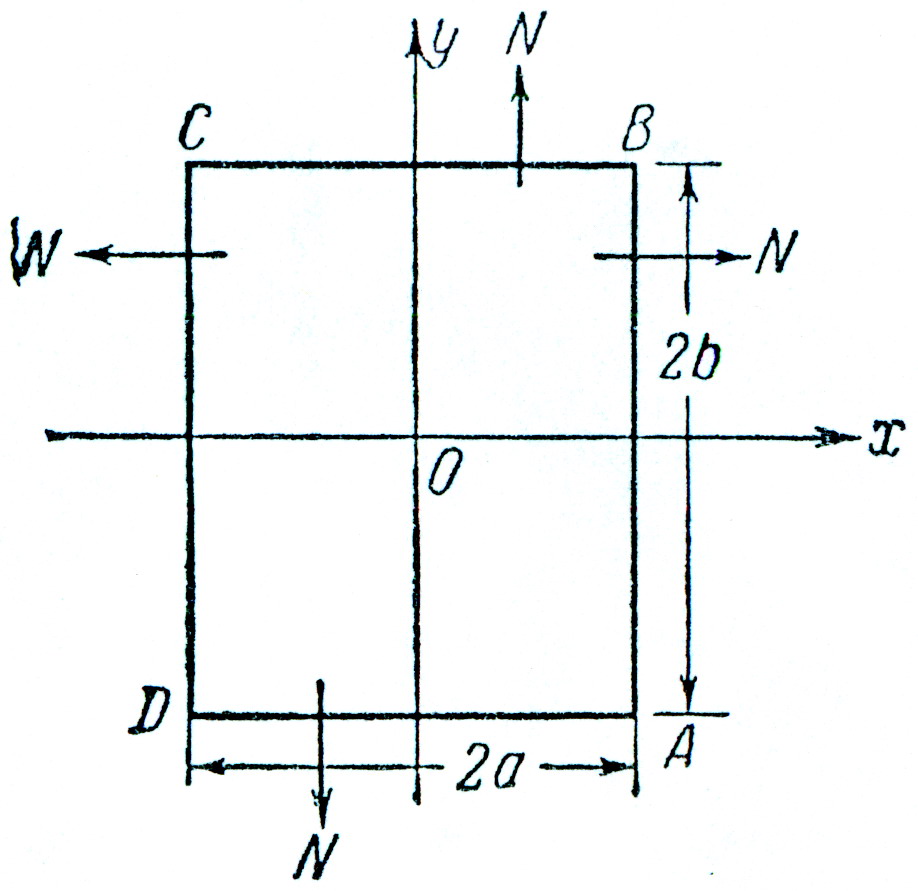
рис.7
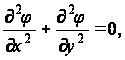 (6)
(6)
и по контору
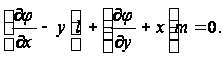 (7)
(7)
На контурных линиях AB и CD, где x=![]() a, будет l=
a, будет l=![]() 1 и m=0 , а на линиях BC и AD имеем l=0 и m=
1 и m=0 , а на линиях BC и AD имеем l=0 и m=![]() 1 . Условие на контуре (7) можно переписать в следующем виде:
1 . Условие на контуре (7) можно переписать в следующем виде:
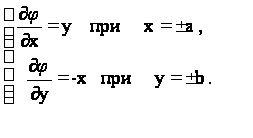 (31)
(31)
Этим условиям можно придать более удобную форму, вводя новую функцию ![]() так, что
так, что
![]() . (32)
. (32)
Легко показать, что для новой функции ![]() основное уравнение по всей прямоугольной области будет иметь вид:
основное уравнение по всей прямоугольной области будет иметь вид:
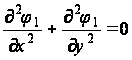 ; (33)
; (33)
условия на контуре будут следующими:
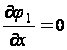 при
при ![]() (34)
(34)
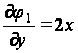 при
при ![]() (35)
(35)
Примем решение уравнения (33) в виде бесконечного ряда
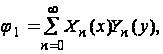 (36)
(36)
каждый член, которого удовлетворяет дифференциальному уравнению; здесь Xn(x) и Yn(y) – функции соответственно только x и y. Очевидно, если решение для ![]() нельзя выразить в форме ряда (36), то мы не сможем найти решение для функции Xn и Yn , удовлетворяющее граничным условиям.
нельзя выразить в форме ряда (36), то мы не сможем найти решение для функции Xn и Yn , удовлетворяющее граничным условиям.
Подставляя Xn(x), Yn(y) в уравнение (33) и обозначая производные штрихами, находим
![]()
Или
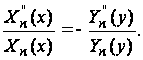
Так как левая часть полученного уравнения является функцией только от x, а правая зависит только от y, то уравнение может быть удовлетворено лишь в том случае, если обе его части равны постоянной величине; обозначим ее через (![]() ) (постоянную берем со знаком минус, так как иначе граничные условия не будут удовлетворяться). Таким образом, мы получаем два обыкновенных дифференциальных уравнения:
) (постоянную берем со знаком минус, так как иначе граничные условия не будут удовлетворяться). Таким образом, мы получаем два обыкновенных дифференциальных уравнения:
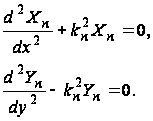
Эти дифференциальные уравнения легко решить с помощью известных методов интегрирования обыкновенных дифференциальных уравнений с постоянными коэффициентами. Решение их будут следующими:
![]() (37)
(37)
![]() (38)
(38)
Рассмотрим теперь условие на контуре (35). Во-первых, можно установить, что выражение
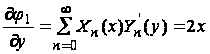
должно иметь одно и то же значение при y=b и y=-b. Это условие может быть выполнено, если производные ![]() являются симметричными функциям от y. Во-вторых, при
являются симметричными функциям от y. Во-вторых, при ![]() будем иметь
будем иметь
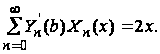
Это условие удовлетворяется, если Xn(x) являются антисимметричными функциями относительно x. Исходя из этих соображений, находим, что c2=c4=0.Условие (34) будет выполнено, если ![]() , или
, или
![]()
Отсюда находим
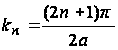 .
.
Поскольку c1 и c2 – произвольные постоянные, функцию можно записать в следующем виде:
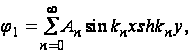 (39)
(39)
Где
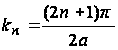 ;
;
постоянные An следует определить таким образом, чтобы удовлетворялось граничное условие (35).
Дифференцируя функцию ![]() по y и подставляя
по y и подставляя ![]() из уравнения (35) получаем
из уравнения (35) получаем
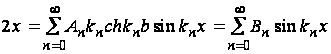 ; (40)
; (40)
здесь для упрощения записи введено обозначение:
![]() .
.
Коэффициенты An можно определить, пользуясь схемой, применяемой при разложении функции в ряд Фурье. Умножим обе части уравнения (40) на ![]() и проинтегрируем все члены по x. Учитывая соотношения
и проинтегрируем все члены по x. Учитывая соотношения
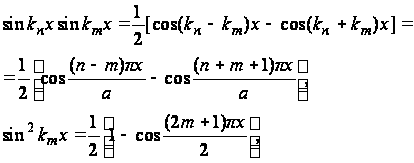
получим
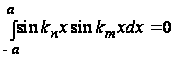 при
при ![]()
= a при m=n
и 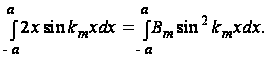
Вычислив значения интегралов в этом выражении, найдем
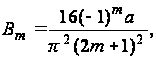
или
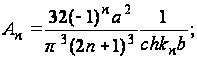
следовательно, решение будет иметь вид:
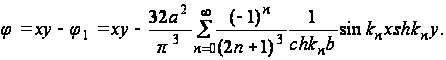 (41)
(41)
Постоянную кручения J можно определить по формуле (15):
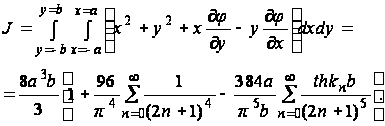
Принимая во внимание равенство
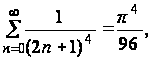
приходим к формуле для J:
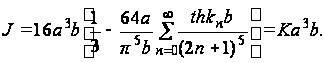 (42)
(42)
В таблице 1.1 даны значения K, соответствующие разным величинам отношения b/a .
Таблица 1.1
| b/a | K | K1 | K2 |
1,0 1,2 1,5 2,0 2,5 3,0 4,0 5,0 10,0
| 2,250 2,656 3,136 3,664 3,984 4,208 4,496 4,656 4,992 5,328 | 1,350 1,518 1,696 1,860 1,936 1,970 1,994 1,998 2,000 2,000 | 0,600 0,571 0,541 0,508 0,484 0,468 0,443 0,430 0,401 0,375 |
Ряд (42) можно записать в виде
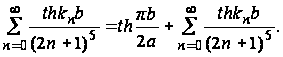
Мы замечаем, что сумма 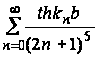 меньше суммы
меньше суммы 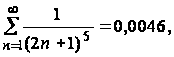 так как
так как 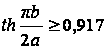 при
при ![]() . Следовательно, первый член ряда дает значение суммы с точностью до 0,5%, и для практических расчетов можно пользоваться приближенной формулой
. Следовательно, первый член ряда дает значение суммы с точностью до 0,5%, и для практических расчетов можно пользоваться приближенной формулой
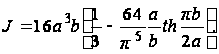 (43)
(43)
После некоторых выкладок находим следующие формулы для касательных напряжений:
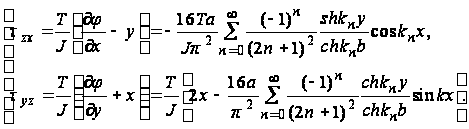 (44)
(44)
Можно показать, что если b>a, то максимальные касательные напряжения имеют место посередине длинных сторон прямоугольника, при ![]() . Подставляя в уравнение (44) значения x=a и y=0, находим
. Подставляя в уравнение (44) значения x=a и y=0, находим
![]()
и
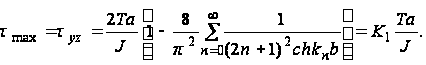 (45)
(45)
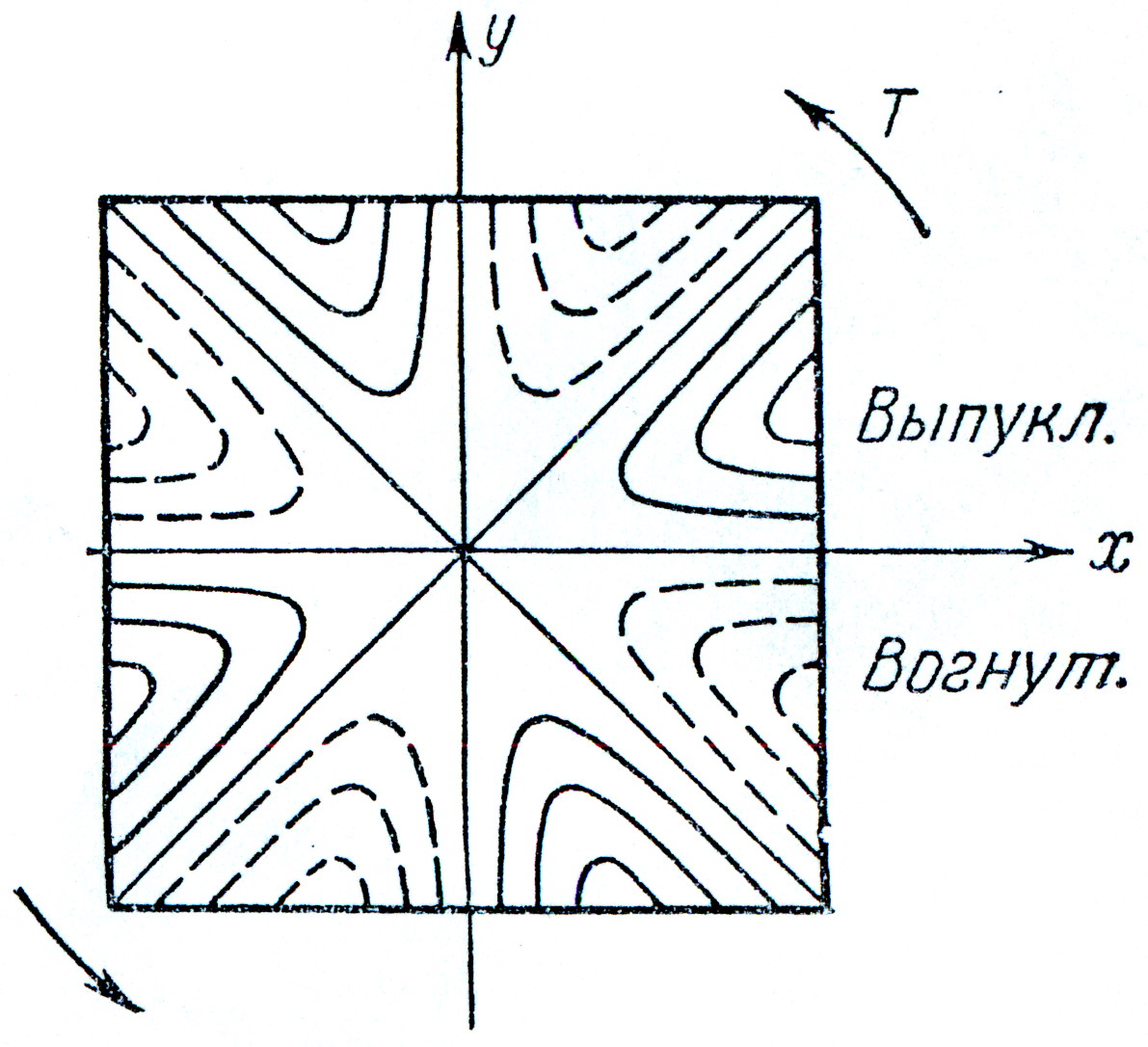
рис.8
Бесконечный ряд в правой части уравнения, которой мы обозначим через K1/2, сходится очень быстро при b>a , и вычисление величины ![]() с достаточной точностью для любого отношения b/a не представляет трудностей. Значение K1, соответствующие различным величинам b/a , включены в табл. 1.1. Подставляя выражения
с достаточной точностью для любого отношения b/a не представляет трудностей. Значение K1, соответствующие различным величинам b/a , включены в табл. 1.1. Подставляя выражения
постоянной кручения J из уравнения (42) в уравнение (45), получаем
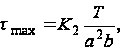 (46)
(46)
где K2 - второй числовой множитель, значения которого также даны в табл. 1.1.
Горизонтали поверхности, для которых ![]() , могут быть легко определены из уравнения для функции
, могут быть легко определены из уравнения для функции ![]() . Для стержня квадратного сечения, т.е. при a=b , горизонтали на рис.8; здесь сплошные линии соответствуют положительным значениям w, а пунктирные – отрицательным, по правилу знаков.
. Для стержня квадратного сечения, т.е. при a=b , горизонтали на рис.8; здесь сплошные линии соответствуют положительным значениям w, а пунктирные – отрицательным, по правилу знаков.
§1.3 Мембранная аналогия
Из примера, разобранного в предыдущем параграфе, становится очевидным, что задачи о кручении стержня более сложной формы поперечного сечения может оказаться весьма трудным. Для приближенного решения задач о кручения стержней различных сечений, часто встречающихся в технике, весьма эффективной оказались так называемая мембранная аналогия. Она основана на математической аналогии между задачами о кручении и о деформации упругой натянутой мембраны, подверженной равномерному поперечному давлению.
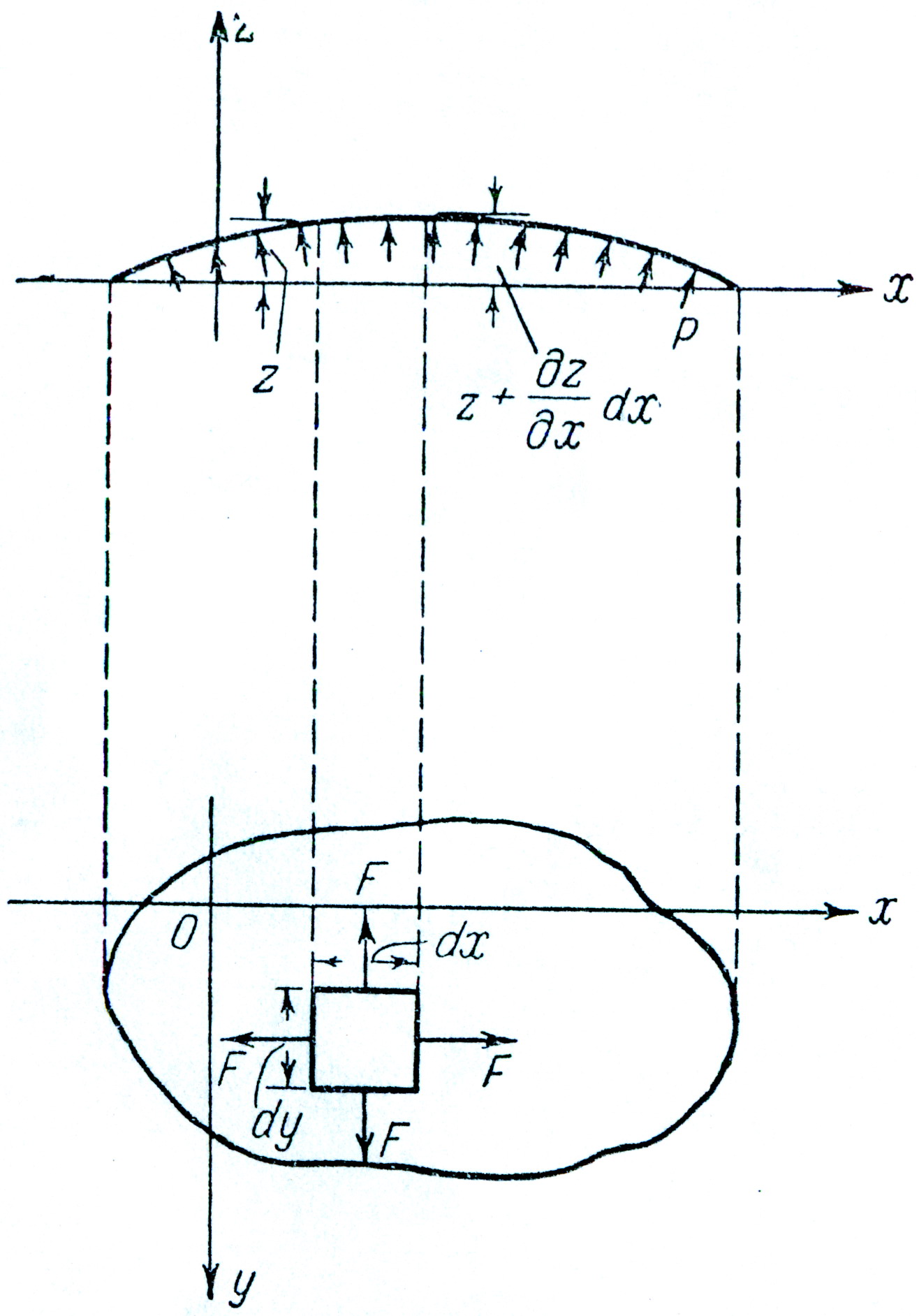
рис.9
Пусть тонкая однородная мембрана (рис.9) имеет постоянное натяжение и закреплена по контуру, который ограничивается кривой, лежащей в
плоскости xy. Если мембрана подвергается равномерному поперечному давлению p, то точки её срединной поверхности получат перемещения z, зависящие от x и y. Рассмотрим условие равновесия бесконечного малого элемента ABCD мембраны после деформации. Обозначим через F постоянное натяжение, приходящееся на единицу длины мембраны. Усилие F, действующее по стороне AD, наклонено к оси под углом ![]() . Так как деформации малы, то можно принять
. Так как деформации малы, то можно принять 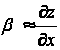 . Прогиб z меняется от точки к точке, поэтому усилие F для стороны BC наклонено под углом
. Прогиб z меняется от точки к точке, поэтому усилие F для стороны BC наклонено под углом
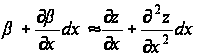 .
.
Таким же путем находим, что углы наклона растягивающих усилий, приложенных по сторонам AB и CD, равны соответственно ![]() и
и 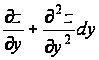 .
.
Складывая составляющие вдоль оси сил, действующих по четырем сторонам, получаем
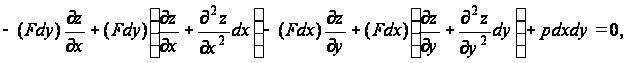
отсюда
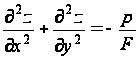 … для области R. (47)
… для области R. (47)
На контуре прогиб мембраны равен нулю. Поэтому граничное условие имеет вид:
z=0 на контуре S. (48)
Вернемся теперь к задаче о кручении. Основное дифференциальное уравнение будет:
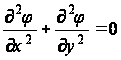 для области R, (6)
для области R, (6)
а граничное условие имеет вид:
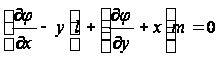 на контуре S. (7)
на контуре S. (7)
На первый взгляд эти соотношения и уравнения (47) и (48) не являются аналогичными. Однако им можно придать идентичную форму, если ввести новую функцию ![]() с помощью соотношений:
с помощью соотношений:
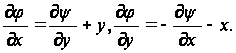 (49)
(49)
Из уравнений (49) имеем
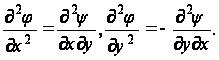
Дифференциальное уравнение (6) обращается в тождество, так как
![]() +
+ ![]() =
= ![]()
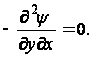
Таким образом, если функция ![]() определяется по формулам (49), то уравнения равновесия будут удовлетворяться тождественно.
определяется по формулам (49), то уравнения равновесия будут удовлетворяться тождественно.
Выражая касательные напряжения ![]() и
и ![]() через функцию
через функцию ![]() , получаем
, получаем
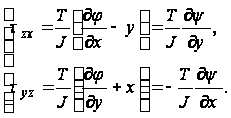 (50)
(50)
Если функция ![]() найдена, то касательные напряжения можно вычислить путем простого дифференцирования. Следовательно, функция
найдена, то касательные напряжения можно вычислить путем простого дифференцирования. Следовательно, функция ![]() представляет собой функцию напряжений; определение функции
представляет собой функцию напряжений; определение функции ![]() равнозначно вычислению напряжений. Далее следует использовать уравнение совместимости. Системе напряжений
равнозначно вычислению напряжений. Далее следует использовать уравнение совместимости. Системе напряжений
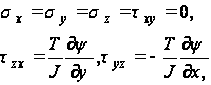
соответствуют компоненты деформации:
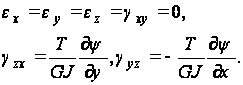
Подстановка этих величин в уравнения совместимости показывают, что первые три уравнения и последнее из них тождественно удовлетворяются. Четвертое и пятое уравнение приводятся к виду:
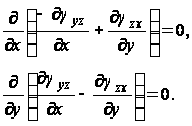
Интегрируя их, находим
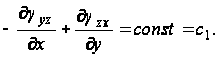
Эту постоянную можно определить, если подставить сюда выражения
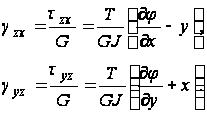
Тогда получим
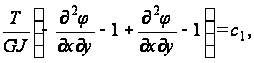
Или
![]()
Подставляя значение с в уравнение совместимости, получим дифференциальное уравнение
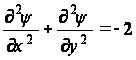 для области R, (51)
для области R, (51)
которому должна удовлетворять функция ![]() . Отметим, что уравнение (51) можно получить непосредственно, продифференцировав уравнение (49) и затем, исключив из них функцию
. Отметим, что уравнение (51) можно получить непосредственно, продифференцировав уравнение (49) и затем, исключив из них функцию ![]() . Но тогда остается нераскрытым то обстоятельство, что уравнение (51) является уравнением совместимости.
. Но тогда остается нераскрытым то обстоятельство, что уравнение (51) является уравнением совместимости.
Граничное условие (8), выраженное через ![]() , имеет вид:
, имеет вид:
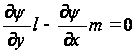 на контуре S.
на контуре S.
В параграфе §1.1 были уже записаны соотношения
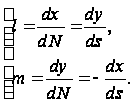 (13)
(13)
Поэтому условие на контуре можно записать в виде
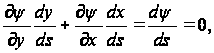 или
или ![]() на контуре S. (52)
на контуре S. (52)
Заметим, что при вычислении напряжений нам необходимы лишь производные от ![]() и что значение постоянной с2 в уравнении (52) не влияет на решение задачи. Поэтому можно принять с2=0. Окончательно решение задачи о кручении сводится к определению функции
и что значение постоянной с2 в уравнении (52) не влияет на решение задачи. Поэтому можно принять с2=0. Окончательно решение задачи о кручении сводится к определению функции ![]() , удовлетворяющей уравнению
, удовлетворяющей уравнению
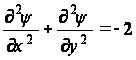 для области R (51)
для области R (51)
и условию ![]() на контуре S. (52)
на контуре S. (52)
Сравнивая эти уравнения с уравнениями для мембраны, мы видим, что между ними имеется полная аналогия, если отношение![]() положить равным 2, и если форма контура мембраны совпадает с формой поперечного сечения стержня. Мембранная аналогия эффективно используется для экспериментального определения функций напряжений. Техника проведения такого эксперимента, а также опытов, связанных с другими аналогиями, подробно описана в специальных пособиях.
положить равным 2, и если форма контура мембраны совпадает с формой поперечного сечения стержня. Мембранная аналогия эффективно используется для экспериментального определения функций напряжений. Техника проведения такого эксперимента, а также опытов, связанных с другими аналогиями, подробно описана в специальных пособиях.
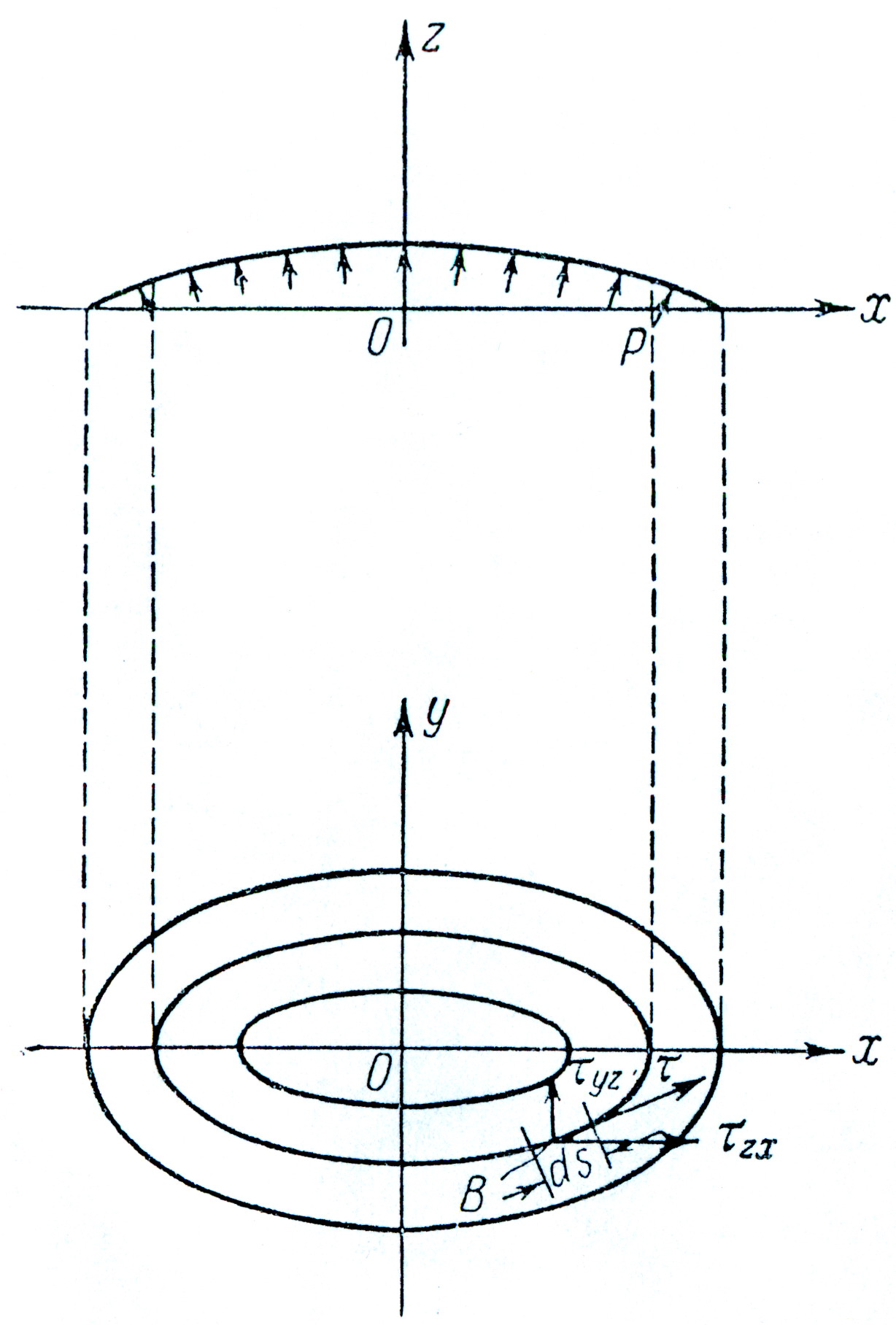
рис.10
Мембранная аналогия может быть использована не только для численного определения натяжений; она дает также наглядную картину напряженного состояния. На рис.10 изображена такая мембрана и нанесены горизонтали изогнутой поверхности. Рассмотрим некоторую точку В срединной поверхности мембраны. Прогиб вдоль горизонтали остается постоянным, так что
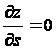 .
.
Пользуясь аналогией, можем написать
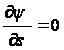 .
.
Из соотношений
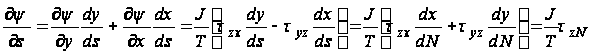
вытекает, что составляющая касательного напряжения, направленная по нормали к горизонтали, равна нулю. Другими словами, касательное напряжение в точке В закручиваемого стержня направлено по касательной по горизонтали, проходящей через эту точку. Величину результирующего касательного напряжения можно найти из следующей формулы:
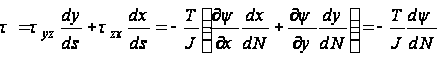 .
.
Следовательно, величина касательного напряжения в точке В определяется уклоном мембраны по нормали к горизонтали, и потому касательные напряжения достигают максимума в тех местах, где горизонтали особенно сгущаются. Рассмотрение поверхности мембраны показывает, что наибольший уклон имеет место на контуре. Отсюда можно заключить, что максимальные значения касательных напряжений будут также в определенных точках контура сечения стержня.
Обратимся к выводу выражения для постоянной кручения J через функцию ![]() . Из формулы (15) имеем:
. Из формулы (15) имеем:
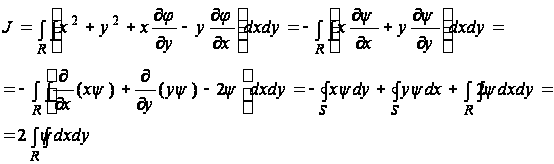 (53)
(53)
Здесь использовано то обстоятельство, что по формуле (52) на контуре S будет ![]() . Из мембранной аналогии вытекает, что постоянная кручения J равна удвоенному объему, заключенному между изогнутой мембраной и плоскостью xy. Полагая c2=0, в (52) мы считали, что величина c2 не влияет на решение задачи. Однако значение J, на первый взгляд, зависит от величины c2. Чтобы выяснить это, допустим, что c2
. Из мембранной аналогии вытекает, что постоянная кручения J равна удвоенному объему, заключенному между изогнутой мембраной и плоскостью xy. Полагая c2=0, в (52) мы считали, что величина c2 не влияет на решение задачи. Однако значение J, на первый взгляд, зависит от величины c2. Чтобы выяснить это, допустим, что c2![]() и подставим
и подставим ![]() вместо
вместо ![]() в последнее из выражений (53). Так как в точках контура
в последнее из выражений (53). Так как в точках контура ![]() , то для них
, то для них ![]() ; следовательно, члены, содержащие контурные значения
; следовательно, члены, содержащие контурные значения ![]() , будут равны нулю так же, как это для функции
, будут равны нулю так же, как это для функции ![]() . Таким образом,
. Таким образом,
![]() .
.
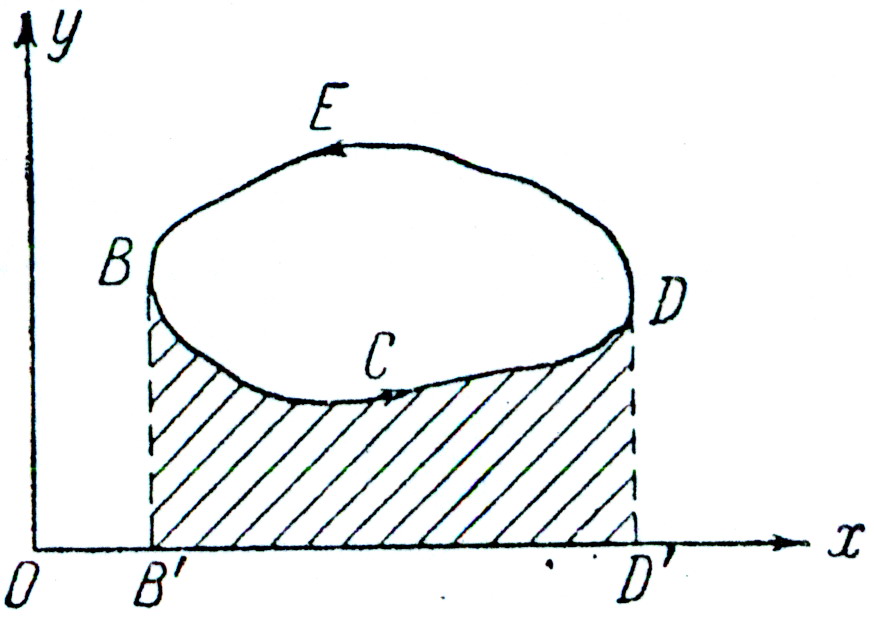
рис.11
Пользуясь, рис .11, приходим к соотношениям
![]() площади BCDD’- площадь BEDD’= -A , (54)
площади BCDD’- площадь BEDD’= -A , (54)
где А - площадь поперечного сечения. Подобным же образом можно показать, что![]() . Но в то же время
. Но в то же время ![]() . Следовательно,
. Следовательно,
![]() ,
,
что совпадает с формулой (53).
§1.4 Кручение тонкостенных стержней открытого профиля
Рассмотрим вначале кручение стержня с поперечным сечением в форме узкого прямоугольника. Из мембранной аналогии заключаем, что влияние коротких сторон прямоугольника распространяется на небольшие участки. Если отношение b/a велико, то в формуле (43) величину ![]() можно приближенно считать равной 1; второй член в скобках становится пренебрежимо мал. Поэтому имеем
можно приближенно считать равной 1; второй член в скобках становится пренебрежимо мал. Поэтому имеем
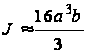 .
.
Обратимся к формуле (45). При значительном отношении b/a величина
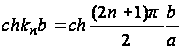
![]()
будет большой, сумма же бесконечного ряда получает пренебрежимо малое значение. В результате получаем
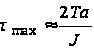 . (55)
. (55)
Если величина J известна, то угол закручивания можно вычислить по формуле
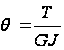 . (16)
. (16)
Обозначим через b1 длину, а через t – толщину прямоугольника (рис.12,а); тогда эти формулы примут вид:
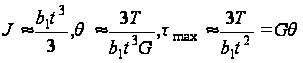 t. (56)
t. (56)
В предыдущем параграфе было показано, что напряжение ![]() равно произведению отношения T/J на максимальный уклон изогнутой мембраны. Из формул (55) и (56) следует, что в случае узкого прямоугольного сечения наибольший уклон изогнутой мембраны равен 2a или t.
равно произведению отношения T/J на максимальный уклон изогнутой мембраны. Из формул (55) и (56) следует, что в случае узкого прямоугольного сечения наибольший уклон изогнутой мембраны равен 2a или t.
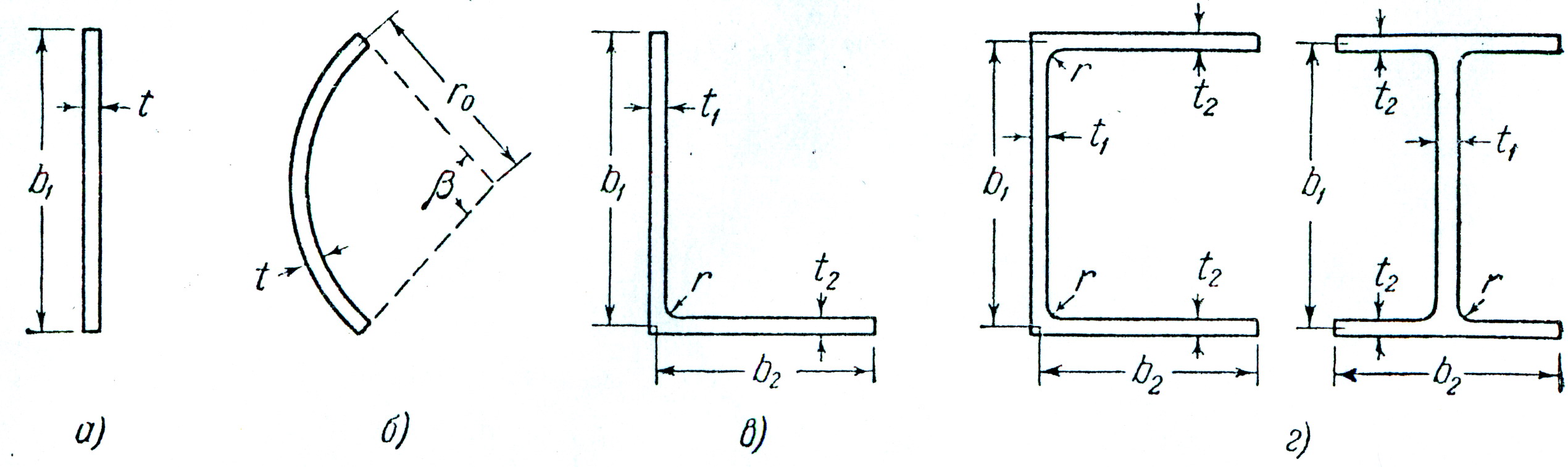
рис.12
Сопоставим теперь изогнутые мембраны с контурами, изображенными на рис.12,а и б. Очевидно, что если площади поперечного сечения их равны между собой, то равными будут и объемы выпучен в изогнутых мембранах. Если толщина t мала, то кривизна сечения в случае (б) незначительно влияет на максимальный уклон мембраны. Поэтому мы делаем вывод, что формула (56) может быть использована при получении приближенных решений и для тонкостенных профилей иной формы. Для поперечных сечений такого типа, который показан на рис.12,б, надо только вместо b1 в формуле (56) подставить развернутую длину дуги. В случае дуги окружности развернутая длина равна ![]() , где
, где ![]() радиус, а
радиус, а ![]() угол, стягиваемый дугой, в радианах.
угол, стягиваемый дугой, в радианах.
Для таких тонкостенных профилей, как уголки, швеллера и двутавры,
вид изогнутых мембран будет таким, как если бы они были натянуты на несколько отдельных узких прямоугольников. Постоянная кручения J будет равна удвоенному объему, ограниченному изогнутой мембраной и плоскостью xy; максимальный уклон мембраны окажется равным ![]() , причем
, причем ![]() большая из величин ti или t2. Следовательно, для уголкового сечения имеем (рис.12, в):
большая из величин ti или t2. Следовательно, для уголкового сечения имеем (рис.12, в):
 (57)
(57)
а для швеллерного и двутаврового сечения (рис.12, г):
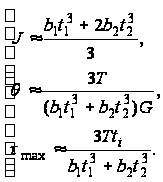 (58)
(58)
Следует заметить, что во входящих углах имеет место значительная концентрация напряжений, зависящая от радиуса закруглений углов профиля. Для малых радиусов закруглений (r=0.1t) Трефц получил следующее уравнение для максимальных напряжений в углах профиля:
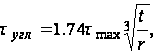 (59)
(59)
где r - радиус закругления угла. Уравнение (59) выведено для случая полок равной толщины. Если же полки имеют различную толщину t1 и t2, то в формулу следует подставить большую из них. Концентрация напряжений во входящих углах изучалось экспериментально, причем была использована аналогия с мыльной пленкой. Отношения ![]() , соответствующие различным значениям отношения r/t, приведены в табл.1.2. Экспериментально полученные величины отношения
, соответствующие различным значениям отношения r/t, приведены в табл.1.2. Экспериментально полученные величины отношения ![]() для малых радиусов закругления ребер профиля значительно меньше вычисленных по формуле (59). Это, вероятно, можно объяснить тем, что при малых радиусах закруглений трудно определить истинные значения
для малых радиусов закругления ребер профиля значительно меньше вычисленных по формуле (59). Это, вероятно, можно объяснить тем, что при малых радиусах закруглений трудно определить истинные значения ![]() .
.
Таблица 1.2
|
|
|
| 1 |
| 2,5 | 2,25 | 2,00 | 1,75 |
![]()
ГЛАВА 2.КРУЧЕНИЕ СТЕРЖНЕЙ, ИМЕЮЩИХ В СЕЧЕНИИ ОКРУЖНОСТЬ ИЛИ ЭЛЛИПС
§2.1 Кручение стержней круглого и эллиптического сечений
Было показано, что для решения задачи о кручении надо найти функцию депла
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Методы интегрирования
- Логіка і множини
Міністерство освіти і науки УкраїниРефератна тему "Логіка і множини"з дисципліни "Дискретна математика"Харків 2011ЗмістВступ1. Логічні
- Николай Бурбаки – математический феномен XX века
Лет тридцать – тридцать пять назад студенты-первокурсники École Normale – высшей математической школы Франции – могли послушать лекции
- Вселенская алхимия. Рождение звёзд
- Случай бесконечной плотности объемного заряда и бесконечного суммарного заряда
М.И. Векслер, Г.Г. ЗегряCлучаи c бесконечной плотностью заряда ρ физически абсолютно невозможны, но они "появляются" в задачах с точечны
- Численное интегрирование функций
Цель реферата состоит в изучение и сравнительный анализ методов численного интегрирования функций; реализация этих методов в виде маш
- Числові характеристики системи випадкових величин та їх граничні теореми
Числові характеристики системи випадкових величин та їх граничні теореми1. Кореляційний момент, коефіцієнт кореляціїКореляційним моме
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

