Конструювання обчислювальної техніки
Дипломна робота
конструювання обчислювальної техніки
Зміст
1. Теплові процеси в РЕЗ
1.1 Теплообмін
1.2 Передача теплової енергії теплопровідністю (кондукцією)
1.3 Теплопровідність крізь стінку
1.4 Теплопровідність вздовж стінок та стержнів
1.5 Способи збільшення теплопровідності
1.6 Передача теплової енергії конвекцією
1.6.1 Конвективна тепловіддача
1.6.2 Вільна конвекція в необмеженому просторі
1.6.3 Вільна конвекція в обмеженому просторі
1.6.4 Конвективний теплообмін при довільному тиску
1.7 Передача теплової енергії випромінюванням
1.8 Складний теплообмін
1.9 Теплові режими РЕЗ
1.9.1 Нагрівання тіла зовнішнім середовищем
1.9.2 Нагрівання тіла внутрішнім джерелом енергії
1.9.3 Розрахунок температури корпуса та нагрітої зони
1.9.4 Максимальна температура РЕЗ
1.9.5 Температура в довільній точці
1.10 Типові теплові моделі РЕЗ
1.11 Вибір загальної системи охолодження РЕЗ
2. ЕОМ як механічна система
2.1 Динамічна модель та її параметри
2.1.1 Приведення мас
2.1.2 Приведення сил
2.1.3 Приведення пружних параметрів
2.1.4 Приведення параметрів дисипації
2.2 Вільні коливання одномасової системи
2.3 Вимушені коливання при гармонічному збудженні
2.4 Коефіцієнт динамічності
2.5 Зменшення вимушених коливань
2.6 Вимушені коливання при періодичному збудженні
2.7 Коливання елементів РЕА типу балок
2.8 Коливання пластин
2.9 Віброзахист обчислювальної техніки
3. Електромагнітна сумісність радіоелектронних засобів
3.1 Проблеми електромагнітної сумісності
3.2 Джерела, приймачі та зв’язки завад
3.3 Застосування еквівалентних електричних схем
3.4 Приклад розрахунку еквівалентної схеми
3.5 Екранування
3.6 Екранування електростатичного поля
3.7 Магнітостатичне екранування
3.8 Електромагнітне екранування
3.9 Електромагнітна сумісність цифрових вузлів
Висновки
Перелік умовних позначень
Список літератури
Вступ
Конструювання є органічною складовою більш широкого процесу, який пов’язаний із розробкою технічного проекту, виробництвом і експлуатацією виробу. Процес конструювання не можна звести до окремих конструкторських рішень, прикладів та рекомендацій. Дуже важливо мати правильне й змістовне уявлення про загальні закономірності конструювання, його проблеми та перспективи. Тому конструювання обчислювальної техніки (ОТ) розглянуто як прикладну наукову дисципліну, що узагальнює методи аналізу та синтезу конструкцій ОТ.
Теорія конструювання обчислювальної техніки формується на основі вивчення та врахування тих фізичних процесів, які реально впливають на її функціональні показники. В першу чергу, це електричні, електромагнітні, теплові та механічні процеси. Ці різні за своєю фізичною природою процеси певним чином взаємопов’язані між собою. Сучасне проектування ОТ вимагає системного підходу, при якому всі фізичні процеси розглядаються у взаємодії. Такий підхід потребує створення складних фізичних та математичних моделей.
Електрична енергія, яку споживає радіоелектронний засіб (РЕЗ), неминуче перетворюється в теплову. При цьому елементи РЕЗ нагріваються і погіршують свої характеристики. Боротьба з перегрівом особливо актуальна в умовах мініатюризації, що потребує детального аналізу трьох видів теплообміну: теплопровідності, конвекції, випромінювання. В багатьох випадках передача тепла відбувається через плоскі й циліндричні стінки, при цьому важливими є способи збільшення теплопровідності. У випадку складних теплових режимів нормальна робота приладів можлива завдяки використанню систем охолодження.
При певних обставинах на базі пружних елементів в ЕОМ можуть виникати та розвиватись механічні коливання. Для визначення рівня коливань складається відповідна динамічна модель. Динамічна модель – ідеалізований в межах поставленої задачі об’єкт з певними характеристиками у вигляді інерційних, пружних, дисипативних та силових параметрів. Важливим питанням є віброзахист обчислювальної техніки, який реалізується завдяки застосуванню різних видів амортизаторів.
Електромагнітна сумісність – здатність виробів нормально функціонувати поруч з іншими виробами в умовах дії між ними та на них додаткових електромагнітних полів при виготовлені та експлуатації. Тому для надійної роботи приладів важливими є способи зменшення завад, екранування електростатичного, магнітного та електромагнітного поля.
1. Теплові процеси в РЕЗ
1.1 Теплообмін
Електрична енергія, яку споживає РЕЗ, неминуче перетворюється в теплову (1, 2). При цьому елементи РЕЗ нагріваються і погіршують свої характеристики. Боротьба з перегрівом особливо актуальна в умовах мініатюризації. Існують два принципово різні методи боротьби з перегрівом:
- зменшення споживаної енергії, яка перетворюється в теплову;
- інтенсифікація тепловідведення з РЕЗ у навколишнє середовище.
Для успішного розв’язку проблеми треба вивчити процеси теплообміну.
Теплообмін – це процес переносу теплової енергії із однієї частини середовища в іншу. Важливо, що теплообмін – необоротний процес. Він визначається різницею температур і проходить в напрямку зменшення температури. Як правило, цей процес іде з середини апарату в зовнішнє середовище.
Розрізняють три види теплообміну (1-3):
· теплопровідність – молекулярний чи електронний процес переносу тепла в суцільному середовищі;
· конвекція – перенесення тепла, пов’язане з макропереміщенням об’ємів рідин та газів;
· випромінювання (радіація) – це явище переносу енергії у вигляді електромагнітних хвиль.
Незалежно від виду теплообміну, тобто незалежно від механізму теплового процесу, його описують за допомогою аналітичного виразу, який має однакову лінійну форму.
Позначимо:
Q – кількість тепла, Дж;
Ф – тепловий потік, Вт.
В такому випадку має місце диференціальна залежність:
![]() , (1.1)
, (1.1)
де τ – час.
Між різницею температур (перегрівом θ) і тепловим потоком має місце залежність
![]() , (1.2)
, (1.2)
де R12 – коефіцієнт пропорціональності, який залежить від природи та стану середовища, а також від механізму теплового процесу. В загальному випадку це складна функція, але досить часто R12 - константа. По аналогії з електричними колами R12 називають тепловим опором.
1.2 Передача теплової енергії теплопровідністю (кондукцією)
Мова йде про передачу тепла в твердих тілах, нерухомих рідинах і газах, коли температура їх окремих ділянок різна. На рис.1.1. зображені ізотермічні поверхні та лінії теплового потоку.
 |
Рис.1.1. Ізотермічні поверхні та лінії теплового потоку
Основним законом теплопровідності є закон Фур’є:
![]() , (1.3)
, (1.3)
де q – поверхнева густина теплового потоку, ![]() ;
;
![]() - температурний градієнт,
- температурний градієнт, ![]() ;
; ![]() - теплопровідність,
- теплопровідність, ![]() .
.
У диференціальній формі зв’язок між тепловим потоком і поверхневою густиною теплового потоку має вигляд
![]() , (1.4)
, (1.4)
де dА – елементарна площа ізотермічної поверхні, через яку проходить тепловий потік.
Якщо тепловий потік однорідний (q=const), то
![]() . (1.5)
. (1.5)
Виведемо формулу для визначення теплового опору, якщо тепловий потік однорідний. З (1.3) та (1.5) слідує, що
![]() .
.
Враховуючи останнє рівняння, з формули (1.2) одержимо:
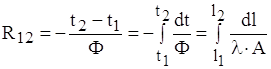 .
.
Дуже часто ![]() . Тоді це рівняння прийме вигляд:
. Тоді це рівняння прийме вигляд:
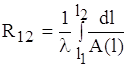 . (1.6)
. (1.6)
З допомогою формули (1.6), виходячи з геометричних особливостей тіла та знаючи коефіцієнт теплопровідності матеріалу λ, можемо визначити тепловий опір ділянки. Знаючи тепловий опір R12 та перегрів θ12, із формули (1.2) одержуємо робочу формулу для визначення теплового потоку на заданій ділянці:
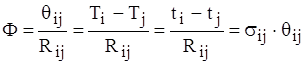 , (1.7)
, (1.7)
де ![]() - тепловий опір ділянки,
- тепловий опір ділянки, ![]() ;
;
![]() - теплова провідність ділянки,
- теплова провідність ділянки, ![]() ;
;  ;
;
![]() - перепад температур (перегрів).
- перепад температур (перегрів).
1.3 Теплопровідність крізь стінку
Стінки є досить розповсюдженими елементами конструкцій обчислювальної техніки. Тепловий опір стінок можна визначати незалежно від умов роботи конструкції та робочих режимів. Розглянемо найбільш типові випадки та виведемо розрахункові формули для визначення теплового опору.
Однорідна поперечна плоска стінка
На рис.1.2. зображена однорідна плоска стінка товщиною δ. Через неї в поперечному напрямку протікає однорідний тепловий потік Ф у напрямі зменшення температури; при цьому ti - температура лівої поверхні стінки, tj - температура правої поверхні стінки, ti > tj.
Теплове коло є тепловим опором Rij з температурними потенціалами на кінцях ti, tj. Формула (1.6) у даному випадку набуде вигляду:
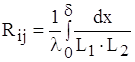 .
.
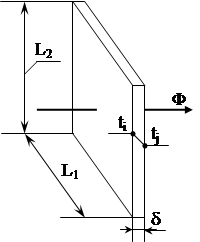 | |||
а) б)
Рис. 1.2. Однорідна поперечна плоска стінка (а) та її теплова модель (б)
Остаточно запишемо її так:
![]() . (1.8)
. (1.8)
Отже, тепловий опір пропорційний товщині стінки δ і обернено пропорційний її площі А та теплопровідності матеріалу λ.
Циліндрична стінка
Нехай однорідний тепловий потік Ф напрямлений у напрямку зовнішньої стінки (рис.1.3).
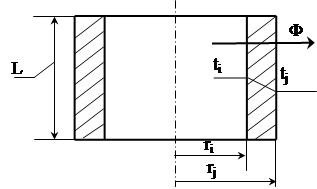 |
Рис.1.3. Циліндрична стінка
Хоча теплове коло, як і в попередньому випадку, складається з одного теплового елемента Rij, розрахункова формула буде іншою. В даному випадку площа поверхні, через яку проходить тепловий потік Ф, є функцією ![]() . Тому формула (1.6) набуває вигляду
. Тому формула (1.6) набуває вигляду
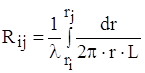 .
.
Остаточно запишемо її так:
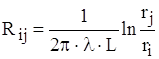 . (1.9)
. (1.9)
Поперечна багатошарова стінка
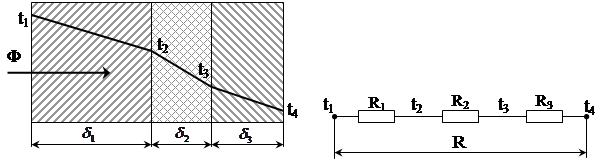
На рис.1.4 зображена поперечна стінка, що складається з трьох шарів. Незмінний однорідний тепловий потік Ф послідовно проходить через кожний шар як через однорідну поперечну стінку площею А.
 |
а) б)
Рис.1.4. Поперечна багатошарова стінка площею А (а) та її теплова модель (б)
Теплове коло є послідовним з’єднанням теплових опорів кожного шару. Тепловий опір всієї стінки визначається як сума теплових опорів елементів. У загальному випадку розрахункова формула набуває вигляду:
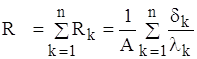 . (1.10)
. (1.10)
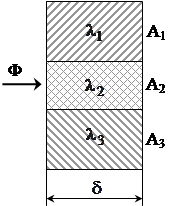
Поздовжня багатошарова стінка
Всі шари стінки мають однакову товщину δ (рис.1.5).
 | |||
 | |||
а) б)
Рис.1.5. Поздовжня багатошарова стінка (а) та її теплова модель (б)
Тепловий потік Ф розподіляється між кожним шаром стінки площею Аk. Кожний шар має свою теплопровідність матеріалу λk. Через поверхню площею Аk проходить тепловий потік Фk, при цьому 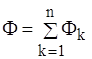 . Теплове коло є паралельним з’єднанням теплових опорів кожного шару. Тепловий опір всієї стінки знайдемо по аналогії з визначенням опору електричного кола. Одержимо розрахункову формулу
. Теплове коло є паралельним з’єднанням теплових опорів кожного шару. Тепловий опір всієї стінки знайдемо по аналогії з визначенням опору електричного кола. Одержимо розрахункову формулу
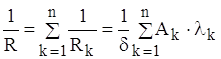 . (1.11)
. (1.11)
1.4 Теплопровідність вздовж стінок та стержнів
Особливістю стержнів та пластин є одновимірний характер розповсюдження тепла. Тепловий потік у стержні рухається вздовж його осі, а в стінці – вздовж стінки. В поперечному напрямку температурний градієнт набагато менший, ніж уздовж стінки чи стержня. До стержнів можна віднести провідники, електроди термопар, тощо. До пластин можна віднести робочий елемент напівпровідникового випрямляча радіаторного типу, окреме ребро радіатора, шасі, на якому змонтовані деталі, тощо.
На рис.1.6 зображений стержень, вздовж якого рухається тепловий потік Ф
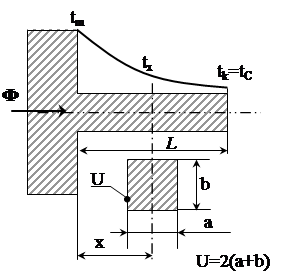 |
Рис.1.6. Тепловий потік стержня
Хоча тепловий потік рухається вздовж стержня, його інтенсивність падає, бо має місце віддача тепла з бокової поверхні стержня в оточуюче середовище. Тому, якщо на початку температура бокової поверхні стержня дорівнювала tm, то в кінці стержня вона падає до значення tk. Якщо L таке, що tk=tC (Фk=0), то для довільного перерізу з координатою х має місце формула:
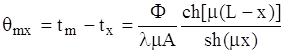 , (1.12)
, (1.12)
де А – площа поперечного перерізу;
U – периметр поперечного перерізу;
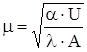 ;
;
α - коефіцієнт тепловіддачі бокової поверхні стержня;
λ - теплопровідність матеріалу;
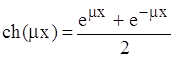 ,
, 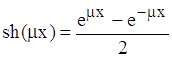 .
.
1.5 Способи збільшення теплопровідності
Ефективна робота теплопроводів визначається не тільки їх геометрією, але й властивостями матеріалу. В першу чергу мова піде про теплопровідність λ, яка входить у всі наведені раніше розрахункові формули кондуктивної теплопередачі.
Матеріал зі значенням теплопровідності ![]() вважається теплопровідним. Тобто такі матеріали в загальному випадку здатні забезпечити відвід тепла від нагрітого елемента, запобігаючи його перегріву. Матеріали зі значенням теплопровідності
вважається теплопровідним. Тобто такі матеріали в загальному випадку здатні забезпечити відвід тепла від нагрітого елемента, запобігаючи його перегріву. Матеріали зі значенням теплопровідності ![]() вважаються теплоізоляційними. Розглянемо теплопровідності основних видів матеріалів більш детально.
вважаються теплоізоляційними. Розглянемо теплопровідності основних видів матеріалів більш детально.
Теплопровідність газів лежить у межах: ![]() (тільки у гелію і водню ці значення у п’ять разів більші). З ростом абсолютної температури Т їх теплопровідність зростає практично лінійно.
(тільки у гелію і водню ці значення у п’ять разів більші). З ростом абсолютної температури Т їх теплопровідність зростає практично лінійно.
Теплопровідність рідин лежить в межах ![]() . Проте якщо в асоційованих рідинах (вода та ін.) з ростом Т значення λ зростають згідно параболічного закону, то у неасоційованих рідин (бензол та ін.) з ростом Т значення λ падають згідно параболічного закону.
. Проте якщо в асоційованих рідинах (вода та ін.) з ростом Т значення λ зростають згідно параболічного закону, то у неасоційованих рідин (бензол та ін.) з ростом Т значення λ падають згідно параболічного закону.
Теплопровідність металів лежить в межах ![]() . У чистих металах при зростанні Т значення λ падає згідно параболічного закону, у сплавах – зростає лінійно.
. У чистих металах при зростанні Т значення λ падає згідно параболічного закону, у сплавах – зростає лінійно.
Значення теплопровідності діелектриків лежить в межах ![]() . З ростом абсолютної температури Т значення λ зростає майже параболічно.
. З ростом абсолютної температури Т значення λ зростає майже параболічно.
Особливе місце займають алмази (природні і штучні). Вони мають особливо високу теплопровідність ![]() . Це визначає їх широке застосування в електронній техніці (напівпровідникові прилади, інтегральні мікросхеми, тощо). Алмази дозволяють зменшити теплові опори між кристалами та корпусом.
. Це визначає їх широке застосування в електронній техніці (напівпровідникові прилади, інтегральні мікросхеми, тощо). Алмази дозволяють зменшити теплові опори між кристалами та корпусом.
Для зменшення теплового навантаження елементів електронних приладів потрібно:
· використовувати матеріали з високим значенням λ;
· збільшувати площу контакту елементів теплопроводів;
· зменшувати шляхи теплопотоків.
Для цього потрібно знімати з контактів лаки, фарби, зменшувати шорсткість поверхонь і збільшувати тиск між ними, в якості прокладок використовувати пасти високої провідності, застосовувати шини між елементами і корпусом, замінювати гумові прокладки на свинцеві, застосовувати самонарізні гвинти.
В якості теплопровідних найбільше застосування знайшли такі матеріали:
· мідь і алюміній для зниження контактного опору;
· кадмій і олово для покриття елементів;
· свинець, мідь, алюміній для виготовлення прокладок.
1.6 Передача теплової енергії конвекцією
1.6.1 Конвективна тепловіддача
Мова йде про передачу тепла з поверхні твердого тіла в газ або рідину, які переміщуються відносно поверхні. Цей процес суттєво залежить від стану нагрітого середовища. Конвекція завжди супроводжується теплопровідністю
![]() ,
,
де q- поверхнева густина теплового потоку;
![]() - теплопровідна складова;
- теплопровідна складова;
![]() - конвективна складова.
- конвективна складова.
Якщо швидкість переміщення V газу чи рідини відносно поверхні тіла падає до нуля, то ![]() . Якщо ж ця швидкість досягає високих значень, то
. Якщо ж ця швидкість досягає високих значень, то ![]() . У більшості практичних задач
. У більшості практичних задач ![]() .
.
Процес конвекції формально (математично) зводиться до процесу теплообміну (тіло - рідина). Цей процес називається конвективною тепловіддачею та виражається формулою Ньютона:
![]() , (1.13)
, (1.13)
де А - площа поверхні тепловіддачі;
![]() - конвективна теплопровідність,
- конвективна теплопровідність, ![]() ;
;
![]() - коефіцієнт конвективної тепловіддачі,
- коефіцієнт конвективної тепловіддачі, ![]() .
.
Формула Ньютона виглядає як лінійна функція, але справа в тому, що коефіцієнт конвективної тепловіддачі складним чином суттєво залежить від багатьох теплофізичних та гідродинамічних факторів. Коефіцієнт конвективної тепловіддачі розглянемо як функцію
![]() , (1.14)
, (1.14)
де ![]() - температура тіла;
- температура тіла;
![]() - температура середовища;
- температура середовища;
![]() - коефіцієнт термічного розширення середовища;
- коефіцієнт термічного розширення середовища;
![]() - теплопровідність середовища;
- теплопровідність середовища;
![]() - теплоємність середовища;
- теплоємність середовища;
![]() - коефіцієнт динамічної в’язкості середовища;
- коефіцієнт динамічної в’язкості середовища;
![]() - густина середовища;
- густина середовища;
![]() - визначальний розмір тіла;
- визначальний розмір тіла;
![]() - прискорення земного тяжіння.
- прискорення земного тяжіння.
В залежності від конкретних умов (1.14) може набути досить простого вигляду. Теорія подібності дає ряд критеріїв, які дозволяють класифікувати задачу визначення αK по значеннях цих критеріїв. Формула (1.14) в залежності від конкретних умов набуває декількох характерних форм, кожна з яких значно простіша базової формули.
1.6.2 Вільна конвекція в необмеженому просторі
Значення αK в першу чергу залежить від стану граничного шару рідини. Для тіл з одним визначальним розміром L (вертикальні плити, стінки, довгі провідники) широкого застосування набула емпірична формула:
![]() ,
,
деPr- число Прантля, 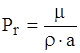 ,
, 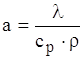 ;
;
Gr- число Грасгофа, 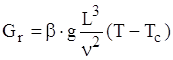 ;
;
Nu- число Нуссельта, ![]() ;
;
c, n – емпіричні коефіцієнти;
m – індекс, який означає, що фізичні параметри рідини беруться для середньої температури
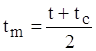 . (1.15)
. (1.15)
В залежності від значення комплексного критерію ![]() розрізняють чотири типових ситуації, які характеризуються певним режимом руху рідини та значеннями С і n (таблиця 1.1).
розрізняють чотири типових ситуації, які характеризуються певним режимом руху рідини та значеннями С і n (таблиця 1.1).
Таблиця. 1.1.
Режими руху рідини
| № | Значення | c | n | Режим руху рідини |
| 1 |
| 0,5 | 0 | Плівковий |
| 2 |
| 1,18 | 1/8 | Перехідний до ламінарного |
| 3 |
| 0,54 | 1/4 | Ламінарний |
| 4 |
| 0,135 | 1/3 | Турбулентний |
Формула (1.15) універсальна в тому розумінні, що стосується різних середовищ (повітря, водень, вуглекислий газ, мастила тощо). Нас ця формула цікавить з точки зору застосування до електронних схем, тобто коли середовищем є повітря.
Форма поверхонь тіл зводиться до трьох базових поверхонь: площина, сфера, циліндр.
Ці поверхні характеризуються одним визначальним розміром L та орієнтацією поверхні в середовищі (повітрі). Орієнтація характеризується значенням параметра N. Основні випадки орієнтації поверхні наведемо у вигляді таблиці 1.2.
Чотири характерні режими конвективної тепловіддачі пов’язують зі значенням емпіричного індексу n і називають законом ступеня n. Розглянемо кожний з чотирьох законів та дамо відповідні формули визначення конвективної тепловіддачі.
Таблиця 1.2.
Орієнтація поверхні в середовищі
| № | Поверхня та орієнтація | L | N |
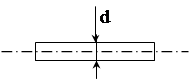
| 1 |
Горизонтальний циліндр | d – діаметр | 1,0 |
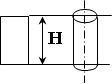
| 2 |
Вертикальна пластина чи циліндр | H – висота | 1,0 |
| 3 |
б) верхня площина | Lmin - мінімальний розмір площини | 0,7 1,3 |
Закон ступеня нуль. Біля поверхні тіла утворюється майже нерухома плівка нагрітого повітря. Теплообмін відбувається практично за рахунок теплопровідності. Такий режим теплообміну має місце при незначних перепадах температур (θ=Т-ТС) для тіл з малими розмірами та плавними формами.
Закон ступеня 1/8. Такий закон має місце при відносно невеликих перепадах температур для тіл з малими розмірами та різкими формами. Наприклад, при охолодженні тонких довгих стержнів. Режим руху теплоносія - перехідний до ламінарного. Інтенсивність теплообміну незначна. Має місце формула:
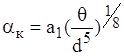 , (1.16)
, (1.16)
де d - діаметр стержня;
![]() . (1.17)
. (1.17)
Закон ступеня 1/4. При цьому законі на поверхні тіла відбувається ламінарний рух. Здійснюється значний конвективний теплообмін. Така картина спостерігається біля ребер радіаторів, на поверхні плоских та циліндричних апаратів середнього розміру. Має місце формула:
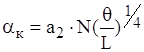 , (1.18)
, (1.18)
де L - визначальний розмір, м;
N - параметр, що визначає орієнтацію тіла;
![]() . (1.19)
. (1.19)
Закон ступеня 1/3. При цьому законі на поверхні тіла відбувається інтенсивний турбулентний рух теплоносія і відбувається інтенсивний теплообмін. Коефіцієнт конвективної тепловіддачі визначається за формулою
![]() , (1.20)
, (1.20)
![]() . (1.21)
. (1.21)
Для визначення коефіцієнта а3 можна скористатись спеціальною таблицею.
Найбільш часто зустрічаються саме закони ступеня 1/4 та 1/3. Тому особливого значення для плоских і циліндричних поверхонь набуває спосіб швидкого визначення ступеня n:
![]() якщо
якщо 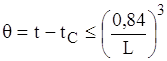 , то n=1/4;
, то n=1/4;
якщо 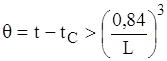 , то n=1/3, (1.22)
, то n=1/3, (1.22)
де визначальний розмір L береться в м.
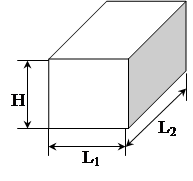
Приклад 1.1. Корпус електричного приладу (рис.1.7) має розмір паралелепіпеда L1 = 0,3 м, L2 =0,4 м, Н = 0,2 м, ![]() . Знайти теплову потужність корпусу при конвективній тепловіддачі.
. Знайти теплову потужність корпусу при конвективній тепловіддачі.
 | |||
 | |||
а) б)
Рис.1.7. Корпус приладу та його теплова модель
Через грані паралелепіпеда паралельно протікають шість теплових потоків. Оскільки бокові поверхні мають однаковий визначальний розмір і розташовані вертикально, то їх можна об’єднати в одну поверхню. Теплове коло (рис.1.7 б) є паралельним з’єднанням трьох теплових опорів: Rбок, Rкр, Rдно.
Конвективна провідність системи визначається як сума трьох провідностей:
![]() ,
,
де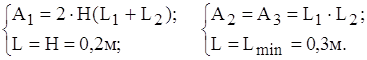
Розглянемо дно і кришку:
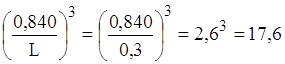 ;
; ![]() ;
;
![]() , тому n=1/4.
, тому n=1/4.
Оскільки визначальні розміри бокових граней менші визначального розміру дна і кришки, то теплообмін по всіх гранях має ступінь n=1/4. Отже маємо такі дані для визначення коефіцієнтів конвективної тепловіддачі бокових граней, кришки та дна відповідно:
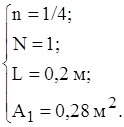
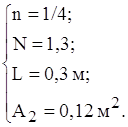
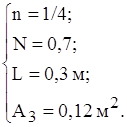
![]() .
.
Згідно формули (1.18) та формули (1.19)
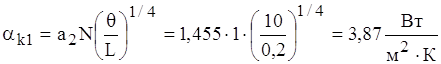 ;
;
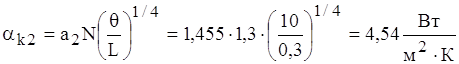 ;
;
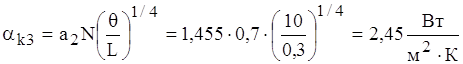 .
.
Отже:
![]()
![]() .
.
Теплова потужність при конвективній тепловіддачі
![]() .
.
1.6.3 Вільна конвекція в обмеженому просторі
Мова йде про тонкий повітряний прошарок, що розміщений між двома близько розташованими площинами (рис.1.8). Складний процес в обмеженому замкнутому просторі прийнято розглядати по аналогії з передачею тепла кондуктивним способом. Це дозволяє уникнути визначення коефіцієнтів конвективної тепловіддачі. У зв’язку з цим користуються ефективним коефіцієнтом тепловіддачі.
У випадку, коли товщина прошарку набагато менша розмірів l1 та l2 (δ<<{l1, l2}), ефективний коефіцієнт тепловіддачі визначається формулою:
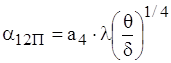 .
.
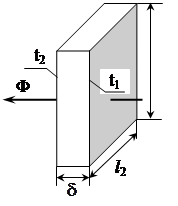 |
Рис.1.8. Тонкий повітряний прошарок
Для повітряних прошарків добуток a2∙λ в широкому діапазоні температур залишається практично сталим і рівним 0,45. Тому:
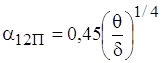 . (1.23)
. (1.23)
У випадку, коли товщина прошарку δ співрозмірна з розмірами l1 та l2 (δ<{l1, l2}), ефективний коефіцієнт тепловіддачі прошарку визначається формулою
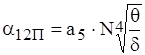 , (1.24)
, (1.24)
де 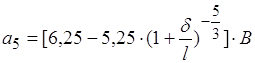 ,
, ![]() (1.25)
(1.25)
Значення В вибирається для середньої температури згідно таблиці 1.3.
Таблиця 1.3.
Значення коефіцієнта В
| 0 | 50 | 100 | 200 |
| B | 0,63 | 0,58 | 0,56 | 0,44 |
1.6.4 Конвективний теплообмін при довільному тиску
Досі в усіх формулах передбачалося, що тиск середовища нормальний, тобто ![]() Па (760 мм. рт. ст.) Насправді, тиск впливає на значення коефіцієнта тепловіддачі. Якщо
Па (760 мм. рт. ст.) Насправді, тиск впливає на значення коефіцієнта тепловіддачі. Якщо ![]() , то
, то
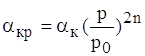 або
або 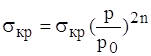 , (1.26)
, (1.26)
де n – ступінь закону теплообміну (n=0, n=1/8, n=1/4, n=1/3).
Отже, вплив тиску можна врахувати після того, як визначені коефіцієнти конвективної тепловіддачі при нормальному тиску.
1.7 Передача теплової енергії випромінюванням
Будь-яке тіло випромінює світлову енергію у вигляді електромагнітних хвиль широкого частотного спектру. Має місце формула:
![]() , (1.27)
, (1.27)
де αВ - коефіцієнт теплопередачі випромінювання.
![]() , (1.28)
, (1.28)
де ![]() - приведена ступінь чорноти;
- приведена ступінь чорноти;
![]() - кутовий коефіцієнт, що показує, яка частина випромінюваної енергії тіла i попадає на тіло j. В багатьох задачах, що стосуються радіоелектронних виробів, можна прийняти
- кутовий коефіцієнт, що показує, яка частина випромінюваної енергії тіла i попадає на тіло j. В багатьох задачах, що стосуються радіоелектронних виробів, можна прийняти ![]() ; f(ti, tj) - функція температур першої поверхні i та другої поверхні j. Згідно закону Стефана-Больцмана значення цієї функції можна обчислити за формулою
; f(ti, tj) - функція температур першої поверхні i та другої поверхні j. Згідно закону Стефана-Больцмана значення цієї функції можна обчислити за формулою
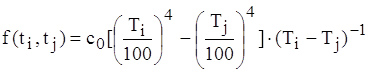 , (1.29)
, (1.29)
де с0 - стала Больцмана, с0 = 5,67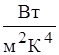 .
.
Значення функції f(ti, tj) зручно визначати з допомогою спеціальної таблиці. Потрібно знати, що при підвищенні температури доля теплової енергії, що випромінюється, збільшується і перевищує конвективну складову.
1.8 Складний теплообмін
Незалежно від виду теплообміну використовується одна розрахункова формула:
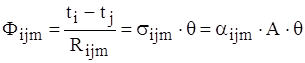 . (1.30)
. (1.30)
Індекс m вказує на механізм переносу тепла: при індукції m≡т, при конвективному теплообміні m≡к та m≡в при випромінюванні. Тому в загальному випадку при наявності всіх трьох теплових процесів
![]() . (1.31)
. (1.31)
Вважаємо, що всі три види теплових процесів протікають паралельно і незалежно.
1.9 Теплові режими РЕЗ
1.9.1 Нагрівання тіла зовнішнім середовищем
Будемо розрізняти два типи температурних режимів:
1) стаціонарний – при якому температурне поле РЕЗ не змінюється з часом τ;
2) нестаціонарний – поле РЕЗ змінюється з часом.
Нехай в тілі довільної форми температура всіх точок однакова. Внутрішні джерела енергії відсутні. Тіло з температурою ![]() переноситься в середовище з температурою
переноситься в середовище з температурою ![]() .
.
Різниця температури тіла і температури середовища змінюється з часом по експоненційному закону (рис.1.9)
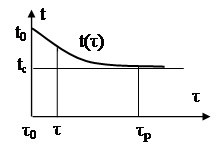 | 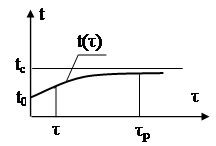 |
а) б)
Рис.1.9. Графік зміни температури при tc=const, Ф=0
Має місце залежність:
![]() , (1.32)
, (1.32)
де m0 – деяка стала, яку називають темпом охолодження або нагрівання тіла, 1/c.
При ![]() , тобто існує сталий режим, який називається регулярним режимом першого роду. З деякого часу
, тобто існує сталий режим, який називається регулярним режимом першого роду. З деякого часу ![]() значення
значення ![]() і режим стає практично сталим.
і режим стає практично сталим.
1.9.2 Нагрівання тіла внутрішнім джерелом енергії
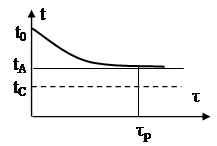
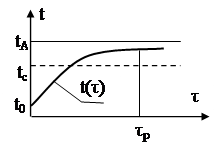
Нехай елементи РЕЗ виділяють тепло, яке утворює тепловий потік потужністю Ф, ![]() . При
. При ![]() наступає стаціонарний режим (рис.1.10). Температура тіла стає рівною
наступає стаціонарний режим (рис.1.10). Температура тіла стає рівною
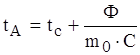 ,
,
де ![]() .
.
Має місце формула аналогічна формулі (1.32):
![]() . (1.33)
. (1.33)
 | |||
 | |||
а) б)
Рис.1.10. Графік зміни температури при tc=const, Ф=const
1.9.3 Розрахунок температури корпуса та нагрітої зони
Середній тепловий потік Ф, що проходить через корпус в оточуюче середовище, практично дорівнює потужності Р, яку споживає електронний пристрій і яка задана. При цьому відомою вважаємо температуру середовища tc, а потрібно знайти температуру корпусу tк. Перегрів корпус – середовище ![]() відповідає потоку Ф згідно формули
відповідає потоку Ф згідно формули
![]() . (1.34)
. (1.34)
Поверхня корпуса приймається ізотермічною поверхнею і тому процес випромінювання однаковий по всій поверхні корпуса площею А. Конвективна тепловіддача здійснюється по різному через бокові грані площею Аб, кришку і дно площею Ак. Перегрів θкс – величина невідома. Коефіцієнт тепловіддачі можна визначити, якщо заданий перегрів θкс. Отже температуру корпусу tk можна визначити, якщо знайти перегрів θКС. Значення θКС шукають з допомогою теплової характеристики Ф=Ф(θКС), яку попередньо треба побудувати. Графік Ф(θКС) проходить через початок координат: Ф(0)=0. Для побудови графіка (рис.1.11) знаходимо ще дві точки, бо графік дещо відрізняється від лінійного. Спочатку задаємось значенням перегріву θ1. Тоді згідно формули (1.34) можемо знайти значення теплового потоку Ф1, який для даного РЕЗ може забезпечити цей перегрів θ1. Значення θ1 та Ф1 визначить точку 1 теплової характеристики. Задавшись значенням θ2 та повторивши розрахунки для визначення Ф2, знайдемо точку 2. Звичайно графік теплово
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Контроллер угловой информации
В настоящее время, в связи с быстрыми темпами развития цифровой техники, число функций, возлагаемых на современное радиолокационное обо
- Контроль электронно-оптических преобразователей
- Концепция построения и этапы совершенствования объединенной системы распределения тактической информации JTIDS
- Корпоративная локальная компьютерная сеть на предприятии по разработке программного обеспечения
В дипломной проекте рассматривается тема «Анализ функционирования корпоративной локальной вычислительной сети на предприятии по разр
- Линзовая антенна РЛС и ППФ
- Люминисценция
- Малошумящие однозеркальные параболические антенны
Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году изв
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.


 Горизонтальна пластина:
Горизонтальна пластина: а) нижня площина
а) нижня площина