Скачать

Комета C/2007 N3 (Lulin)

За все время, проведенное в Малой Академии Наук, мне удалось пронаблюдать, сфотографировать и изучить несколько комет. По двум из них, самым ярким и знаменитым я написал работы. Это были комета 73Р Швассмана-Вахмана 3, которая в 2006 году распалась на множество фрагментов, подобно комете Шумейкеров-Леви 9, и выдающаяся комета 2007 года 17Р Holmes, внезапно вспыхнувшая и, тем самым, повысившая свою яркость более, чем в 400 000 раз. Все эти работы были основаны на живых фотографиях этих комет. Однако, в прошедший год меня постигла неудача и единственная, хоть как-то проявившая себя комета, на которую я возлагал большие надежды в написании будущей работы, пролетела в самый дождливый период, дав возможность в редких проявлениях между тучами запечатлеть комету С/2007 N3 Lulin на пленку всего 5 раз за 2 ночи наблюдений. Но, я не стал искать новую тему для будущего творческого взноса, потому, что меня очень заинтересовало очень быстрое движение этой кометы по звездному небу. Я решил узнать, откуда такая скорость передвижения и как она связана с орбитой кометы? Для этого я попытался сам рассчитать элементы ее орбиты, начертить саму орбиту, а также, по возможности, сделать другие вычисления, исходя из 5 фотографий кометы Лулина.

ОБЩИЕ СВЕДЕНИЯ

Краткая история изучения комет:

Ещё в древности человек мог наблюдать прекрасные хвостатые светящиеся образования на небе, которые, завораживая своим видом, внезапно появлялись и исчезали куда-то. Эти объекты назвали кометами, что означает «длинноволосые», «косматые».

Первое письменное упоминание о появлении кометы датируется 2296г. до н. э. Движение кометы по созвездиям тщательно наблюдалось китайскими астрономами. Научно обосновать явление комет первым попытался Аристотель. На принадлежность комет к Солнечной системе впервые указал Э. Галлей. Джованни Вирджинио Скиапарелли впервые показал, что рой кометных тел, сопровождает Солнце в его движении среди звёзд. Этот рой был назван облаком Оорта. Эрнст Юлиус Эпик установил, что ежегодно нашу Солнечную систему покидают несколько наблюдавшихся комет. Известный советский астроном Борис Александрович Воронцов-Вельяминов продолжил идеи Эпика и высказал предположение о существовании межгалактического кометного фона.

За прошедшие двести лет астрономия совершила гигантский прорыв в понимании законов строения и эволюции комет. В наши дни для изучения комет используются не только наземные средства наблюдений, но и возможности космических аппаратов.

Строение. Состав комет:

У комет, приблизившихся к Солнцу, различают «голову» и «хвост». Центральная часть головы кометы называется ядром. Ядро -это небольшое компактное тело, являющееся конгломератом каменной и ледяной пород. Диаметры ядра колеблются в пределах от 0,5 до 20 км, масса составляет 10 в 10 степени кг. Оно, в основном, состоит из смеси льдов различной природы.

Ядро кометы окутывает оболочка кома, которая является вторичным образованием, т. к. состоит из вещества, выброшенного из кометного ядра.

Под действием светового давления и корпускулярных потоков образуется хвост. Хвост кометы - длинные струйные образования из головы кометы в противоположную от Солнца сторону. Хвост кометы состоит из улетучивающихся из ядра под действием солнечных лучей молекул газов и частиц пыли. Хвосты различают: пылевой, газовый и аномальный.

Природа комет:

Вдали от Солнца температура кометного ядра близка к абсолютному нулю. На расстоянии примерно 5а.е. от Солнца температура на поверхности кометного ядра становится -140 градусов Цельсия. Начинается процесс испарения льдов. При испарении летучих веществ на поверхности ядра образуется корка, препятствующая дальнейшему испарению газов. Толщина корки увеличивается с течением времени. Это явление называется «кометная старость». Кометам свойственно "омолаживаться". Это происходит при столкновениях комет между собой или с астероидами. Сохранению молодости комет способствует их выброс в облако Оорта. Механизм столкновения комет может приводить не только к их омоложению, но и к дроблению кометных ядер на более мелкие. Известны "микрокометы" и "миникометы".

Кометы делят на два основных класса в зависимости от периода их обращения вокруг Солнца:

Короткопериодическими называют кометы с периодами обращения менее 200 лет, а долгопериодическими - с периодами более 200 лет. Все короткопериодические кометы являются членами разных кометно-планетных семейств больших планет.

Общая теория об элементах орбиты

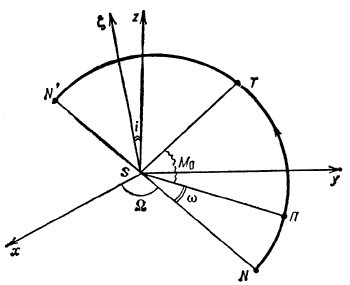
Рис. 1

Элементы орбиты - величины, характеризующие орбиту небесного тела, а также положения тела на орбите.

Орбита небесного тела, движущегося в поле тяготения др. тела, представляет собой кривую второго порядка (конич. сечение), в одном из фокусов которой находится центр масс двух тел (притягивающий центр). Данное определение относится к случаю, когда взаимодействующие тела сферически-симметричны или же находятся на столь большом расстоянии, что отклонение их формы от сферической не сказывается существенно на силе взаимодействия.

Точка орбиты тела, ближайшая к притягивающему центру, наз. перицентром, а наиболее удаленная - апоцентром. В данном случае это перигелий и афелий.

На рис. 1 S^xy - основная координатная плоскость. Здесь это плоскость земного экватора.

Ось S^x направлена в основную точку, за которую для орбит тел в Солнечной системе чаще всего принимают точку весеннего равноденствия (одну из точек пересечения экватора с эклиптикой). Плоскость NПN' - плоскость орбиты небесного тела, П - перигелий орбиты, - полюс орбиты (он находится на прямой, проходящей через перигелий и перпендикулярной к плоскости орбиты), T - положение небесного тела на орбите.

Прямая NSN', по которой плоскость орбиты NПN' пересекается с основной координатной плоскостью S^xy, называется линией узлов. Полупрямая SN, которую небесное тело пересекает, показывает положительное направление линии узлов. Если движение небесного тела происходит против часовой стрелки для наблюдателя, находящегося в полюсе орбиты , то точка N называется восходящим узлом орбиты, а N' - нисходящим узлом. Угол  между осью S^x и полупрямой SN наз. долготой восходящего узла. Этот угол отсчитывается от оси S^x в сторону оси S^y от 0 до 360^o. Угол i между плоскостью орбиты и плоскостью S^xy называется наклоном орбиты. Наклон может иметь все значения от 0 до 180^o. Если , то движение наз. прямым, если же , то обратным. Угловое расстояние  линии SП от линии узлов SN наз. расстоянием перигелия от узла или аргументом перигелия. Угол  отсчитывается в направлении движения тела от 0 до 360^o.

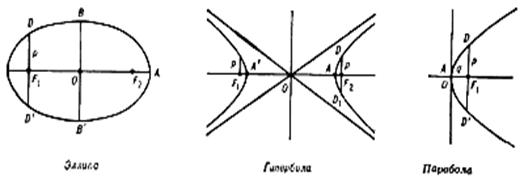
Рис. 2

Величины составляют первую группу элементов орбиты, первые два из них характеризуют положение плоскости орбиты, а третий - ориентацию орбиты в этой плоскости.

Размер орбиты и ее форму характеризуют элементы и e - параметр и эксцетреситет (рис. 2). Эксцетреситетом орбиты e наз. отношение расстояния между фокусами F¹F²=2c этой орбиты к расстоянию между ее вершинами A и A'. Расстояние между ее вершинами обозначают 2a, а величину a наз. большой полуосью орбиты, так что e=c/a. Для нашей параболической орбиты c=a, поэтому e=1. Половина фокальной хорды DD' орбиты, перпендикулярной к ее оси, носит название фокального параметра и обозначается буквой . Вместо двух элементов и e для параболы используют один элемент q=p/2 - перигелийное расстояние (на рис. 2 отрезок AF¹). Движение по круговой орбите является частным случаем движения по эллипсу (e=0).

Положение небесного тела на орбите в некоторый начальный момент времени t⁰ определяется его угловым расстоянием от линии апсид. Этот угол обозначается через M⁰ и наз. средней аномалией в эпоху. Часто в качестве элемента выбирают момент времени  прохождения небесного тела через перигелий орбиты.

Элементы наз. кеплеровскими элементами. Они определяют орбиту независимо от того, является ли она эллиптической, гиперболической или параболической.

КОМЕТА C/2007 N3 (Lulin)

Общие сведения о комете

Любители астрономии хорошо помнят неожиданную вспышку кометы Холмса, всего за сутки превратившую эту комету из телескопического объекта в объект, видимый невооруженным глазом. Но прошло чуть более года, как Природа уготовила нам новый сюрприз. Конечно, не такой яркий, но не менее загадочный.

КометаC/2007 N3 (Lulin), проще говоря – комета Лулина, была открыта сравнительно недавно - в июле 2007 года двумя астрономами Цюань Чжи Е (Quanzhi Ye) и Чи Шэн Линь (Chi Sheng Lin). Свое интересное название она получила в честь тайваньской обсерватории Лулин, где работал один из первооткрывателей.

Комета Lulin представляет собой очень интересный и необычный объект, который движется по своей орбите в противоположную всем планетам сторону. При этом угол наклона орбиты кометы к плоскости эклиптики очень мал – всего 1,6° (или 178, 38⁰). Комета движется по параболической траектории и, вероятно, это ее первый визит к Солнцу. Орбита кометы пересекает пути всех планет-гигантов Солнечной системы (перигелий кометы - между орбитами Земли и Марса), но ни одна из них на нее не оказала заметного влияния.

Еще в начале июля 2008 года блеск кометы Lulin был около 11m, но уже к октябрю увеличился до 9,5m. В конце декабря ее блеск оценивался в 7,6m. Максимального сближения с Землей комета достигла 24 февраля 2009 года, когда геоцентрическое расстояние составило 61 миллион километров. Ее блеск составил 5m, при этом скорость перемещения кометы по небесной сфере составила примерно 5° в сутки. Это объясняют ее «обратным» движением.

В период наилучшей видимости в феврале 2009 года комета двигалась по созвездиям Весов, Девы, Льва и Рака. Комета прошла близ ярких звезд Спики и Регула. При наблюдении на неё через бинокль или телескоп, наблюдали видимое движение кометы на фоне звёзд. 14 января комета находилась на ближайшем расстоянии от Солнца. А в ночь с 23 на 24 февраля комета Lulin прошла всего в 2° южнее Сатурна. Именно в эту ночь были относительно неплохие погодные условия, и нам удалось запечатлеть на пленку это прохождение.

Ко всему прочему, комета Lulin, подобно комете 17P Holmes, имела необычный зеленоватый оттенок ( >> ). Характерный цвет комете Лулин придали входящие в состав ее ядра молекулы углерода и ядовитого газа дициан, которые под воздействием солнечных лучей и в условиях безвоздушного пространства создают зеленоватое свечение.

И, пожалуй, главной особенностью этой замечательной кометы был "сброс" кометой Лулин своего нормального хвоста ( >> ). Аномальный хвост кометы, или "антихвост", при этом не изменился.

Природа феномена, как и очень многое в природе комет вообще, далека от понимания. Эффект сброса хвоста наблюдался при столкновении в 2007 году кометы Энке с облаком солнечного вещества, выброшенного протуберанцем. Однако можно ли в данном случае говорить о выбросе солнечного ветра, неясно.

На представленных астрономами снимках сгусток, отделившийся, от ядра, отстоит от него примерно на полградуса - диаметр полной Луны. К тому же Солнце находится не просто в абсолютном минимуме своей активности, но и в минимуме, по необъяснимым причинам необыкновенно затянувшемся.

Расчет элементов орбиты кометы Lulin

Как я уже упоминал, комета Lulin, к несчастью, пролетела в самый дождливый период, не дав ее толком сфотографировать. К тому же, мешала яркая Луна. Но, я не отчаялся и решил узнать, почему комета имела довольно большую скорость на звездном небе, рассчитав ее орбиту.

Для нахождения элементов эллиптической орбиты достаточно знать два гелиоцентрических положения небесного тела на два момента времени. При наблюдении с Земли надо иметь для этого три положения на небесной сфере. На тот момент времени у меня имелось 4 фотографии кометы, сделанные ночью 24 февраля и один снимок с ночи 19 февраля, т. е. два основных положения кометы. Я постарался, как можно точнее вычислить эфемериды кометы в этих положениях. Получились такие результаты:

На 19.02.09 в 5ч. 20м.

α = 12h 30΄ 36΄΄

δ = -2º 54΄47΄΄

На 24.02.09 в 2ч. 00м.

α = 11h 1΄ 7΄΄

δ = +6º 18΄

Эфемериды третьего положения мне пришлось взять в готовом виде в Интернете:

На 10.03.09. в 0ч. 00м.

α = 7h 54΄ 18΄΄

δ = +20º 13΄ 11΄΄

Для начала, выполнив необходимые вычисления, я перевел экваториальные координаты (α, δ) этих трех положений в эклиптикальные (X, Y, Z).

За единицу времени принял средние солнечные сутки, за единицу расстояния – астрономическую единицу.

1. Находим для всех трех моментов величины:

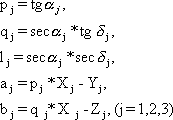
Далее находим:

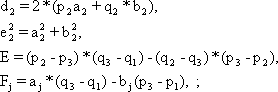
2. Находим величины:

 ,

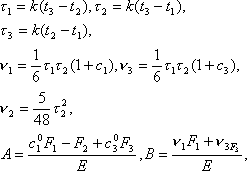 где k = 0,017 202 1;

3. Решаем систему двух уравнений с двумя неизвестными x₂ и r₂:

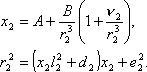
Применяя так называемый метод последовательных приближений, выбираем произвольно некоторое начальное значение x₂ = (x₂)₀, после чего находим (r₂)₀ и из следующего уравнения вычисляем значение x₂ = (x₂)₁. Если бы начальное значение x₂ было выбрано правильно, т.е. удовлетворяло бы уравнениям, то тогда (x₂)₀ = (x₂)₁.В противном случае (x₂)_0≠ (x₂)₁. Тогда с новым значением (x₂)₁ вычисляем аналогичным путем следующее приближение (x₂)₂. Если (x₂)_1≠ (x₂)₂, то вычисляем дальше и так до тех пор, пока два последующих приближения не сойдутся в пределах заданной точности.

4. Далее находим:

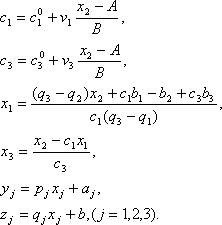
Координаты (x_j ,y_j, z_j), j = 1,2,3 – прямоугольные гелиоцентрические экваториальные координаты тела в моменты 1, 2, 3 соответственно. Дальнейшее вычисление элементов орбиты может быть проведено по двум гелиоцентрическим положениям. Обычно выбирают два крайних положения, но я взял два положения, соответствующие моим снимкам 19.02 и 24.02.2009.

5. Вычисляем:

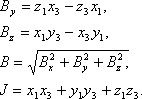
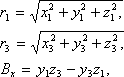
где x, y, z₁ – эклиптические координаты кометы 19.02, а x, y, z₃ – координаты на 24.02.

6. Находим элементы Ω (долготу узла), i (наклонение) по формулам:

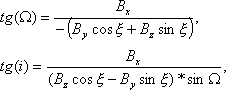
После проведения этих вычислений, у меня получились такие результаты:

Ω ≈ 338,8º

i ≈ 178, 4º, что означает обратное движение кометы по орбите с наклоном самой орбиты к эклиптике на 1,6º.

7. определяем параметр орбиты р:

,

где Y вычисляем с помощью непрерывной дроби:

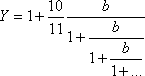
р ≈ 2,6896 а. е.

Имея в распоряжении параметр орбиты, по очень простой формуле q=p/2 можно высчитать q (перигелийное расстояние) орбиты кометы Lulin.

q = 1,3448 а.е.

Значит, перигелий орбиты, с учетом погрешностей, находится где-то около орбиты Марса.

8. Эксцентриситет орбиты кометы Лулина, по определению равен 1, исходя из ее параболической орбиты. В связи с этим же мы не можем высчитать несуществующую большую полуось. Следовательно, такой элемент, как средняя аномалия М = 0.

9. Последним элементом находим аргумент перигелия ω. Я не нашел формул для его вычисления, поэтому мне пришлось считать аргумент перигелия и момент для прохождения (t₀) перигелия с помощью специальной компьютерной программы.

В итоге вышло:

 ω ≈ 152,2º

 t₀ ≈ 18. 01. 2009

Итак, получились такие элементы орбиты кометы С/2007 N3 Lulin:

i ≈ 178, 4º

Ω ≈ 338,8º

q ≈ 1,3448 а.е.

e = 1

M = 0

ω ≈ 152,2º

t₀ ≈ 18. 01. 2009

Если сравнить с теми, что даны во Всемирной сети:

Наклон орбиты, гр 178,3704

Долгота восходящего узла, гр 338,4791

Перигелийное расстояние, а.е. 1,209265

Эксцентриситет орбиты 0,999581

Аргумент перигелия, гр 136,9164

Дата прохождения перигелия 10. 01.2009

Видно, что погрешность в моих вычислениях не очень большая, даже, можно сказать, приемлемая.

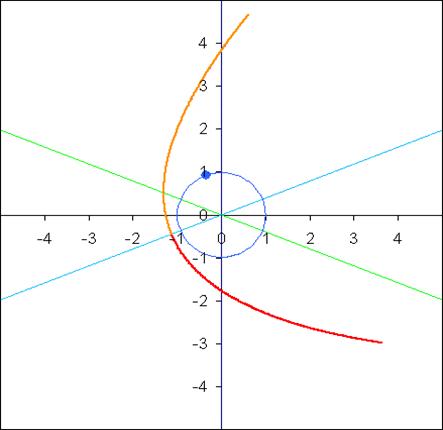
Теперь, зная элементы орбиты кометы Лулина, можно начертить и саму орбиту:

ЗАКЛЮЧЕНИЕ

Таким образом, мне удалось изучить, немного пронаблюдать и сфотографировать еще одну неординарную комету C/2007 N3 (Lulin), таящую в себе много загадок. В одной из них я смог разобраться – это ее очень быстрое движение на небе среди звезд из-за нестандартного расположения орбиты кометы, но вторая – отделение хвоста – так и остается неразгаданной.

Благодаря этой комете, точнее, благодаря неблагоприятным условиям ее видимости, мне, конечно, не удалось сделать так много ее фотоснимков, как прошлых неординарных комет, но, зато на примере кометы Lulin я смог разобраться и изучить небольшой, однако, довольно непростой раздел астрометрии, такой, как вычисление кеплеровских элементов параболической орбиты, о котором раньше я знал лишь азы.

В дальнейшем я планирую подробней и более глубоко изучить комету Lulin, исходя из имеющихся данных, попытаться рассчитать ее нормальную скорость, позиционный угол хвоста и другие элементы.

СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ

1. Детская энциклопедия «Аванта» Астрономия.

2. Учебник для 11 класса Е. П. Левитан

3. Учебник для 11 класса Б. А. Воронцов-Вельяминов

4. Общий курс астрономии М. Кононович.

5. Интернет-ресурсы:

A. http://www.thinkquest.ru/library/40407/trip05

B. http://www.rian.ru/science/20090203/160863028

C. http://meteoweb.ru/astro/clnd023

D. http://www.astrogalaxy.ru/797