Скачать

Классическая физика: самоорганизующиеся системы и микромир

Содержание:

1) Предисловие

2) Простейшие самоорганизующиеся системы

3) Самоорганизующиеся модели упругих тел

4) Неизлучающий атом Резерфорда

5) Общее представление об упругих телах

6) Движение и реорганизация упругих систем

7) Принцип относительности для мира самоорганизующихся систем

Предисловие

Я, автор этого изложения, имею профессию, в основе которой лежит классическая теория Фарадея-Максвелла. Это мой инструмент - проверенный, надежный, безупречный. Однако академическая физика в тысячах книг, брошюр и лекций уверяет, что эта теория несостоятельна, не способна объяснить эксперимент Майкельсона и противоречит якобы факту: "электроны в атомах не излучают". Но ведь факт не таков. Ведь не излучает лишь атом в целом - система из ядра и электронов, факт именно таков, и он имеет в классической теории объяснение, специалисту очевидное. Здесь факт "атом не излучает" подменяется на его ложную трактовку "электроны не излучают". Зачем? Почему-то современная физика, ниспровергая классическую, никогда не приводит доказательств, а лишь уверяет, пропагандирует, подавляет ссылками на авторитеты и мировую науку, повторяет: "Это смешно, нелепо, это попытка спасти теорию". Если бы она была права, то не нуждалась бы в этих недостойных средствах убеждения.

Явная необъективность вызывает сомнения: а были ли вообще перед классической теорией те тупиковые проблемы, о которых говорит нам ее противник? Или их можно решить сегодня, на современном уровне знаний? Пришлось заняться проверкой.

Для решения вопроса о размерах движущихся тел понадобилось искусственное упругое тело, состоящее из макроскопических "атомов" и макроскопических расстояний между ними, которое можно было бы построить в реальности, как изделие. Дело в том, что размеры тел естественных - это сумма межатомных расстояний, скрытых в микромире и недоступных для объективного анализа. Нужен пример тела, в котором расстояния доступны для изучения.

Искусственное упругое тело - это самоорганизующаяся группа из двух, трех и т.д. одинаковых электромагнитных осцилляторов, которые излучают волновые поля и удерживаются на устойчивых расстояниях друг от друга этими же полями и электромагнитными силами, составляя единое упругое тело. В качестве осцилляторов можно для начала применить автоколебательные излучающие устройства, например, излучающие генераторы СВЧ с автономным энергопитанием, и оставить их свободно плавать в жидкости или на ее поверхности. При определенных условиях генераторы самопроизвольно входят в синхронизм, создают поле стоячих волн и располагаются в пучностях магнитного поля на устойчивых расстояниях друг от друга, образуя упругую структуру, в какой-то степени упорядоченную.

Поскольку классическая физика не имеет иных средств построения упругих тел, и в макромире нет иных полей, способных объединять элементы в единое упругое тело, такие системы становятся единственно возможными физическими моделями тел. Такое тело и само по себе - новый, принципиально важный физический объект.

Искусственное тело вещественно, реально и бесспорно, оно может быть создано. Его размеры образованы хорошо известными полями и силами, здесь неуместны постулаты и философские рассуждения. Свойства размеров здесь нетрудно выяснить, мысленно погружая тело в движущиеся "светоносные" (электромагнитные) жидкости. Оказалось, что Лоренц и Фицджеральд были правы: размеры явно зависят от скорости течения "светоносной" среды относительно неподвижного тела, от скорости электромагнитных волн в этой среде, меняясь пропорционально длинам стоячих волн, которыми связаны в единое целое. Авторы учебников столь же явно не правы.

Спор о размерах тел, оказывается, решался удивительно просто, и мог быть решен в рамках классических теорий еще в 1911 году, сразу после открытий Резерфорда, когда стало известно, что размеры тел - это сумма расстояний. Но этого не произошло. Простейшие самоорганизующиеся системы, дающие решение проблем вековой давности, как и физические модели тел, остались неизвестными академической физике.

На вопросы о том, почему не излучается в пространство и не иссякает энергия электромагнитных движений в атомах, молекулах, телах и прочих системах микромира, тоже есть простой ответ, очевидный, можно сказать, еще с 1903 года, когда Гамильтон нашел общее решение волнового уравнения электродинамики для сферических координат. Из этого решения и следуют ответы: два, три или более объектов, излучающих электромагнитные поля в пространство, могут вместе составлять систему, в пространство не излучающую, даже если расположены не один внутри другого, а на расстояниях друг от друга. Их излучения в дальнем пространстве могут взаимно погашаться. Имеют место также явления, приводящие такие системы к неизлучающему состоянию. Таким образом, самоорганизующиеся системы могут сохранять в себе электромагнитную энергию, не излучая ее вовне, и быть достаточно полными моделями упругих тел, молекул, атомов и прочих систем микромира.

Так классическая теория начинает объяснять микромир, не изобретая особых полей и сил иной природы, постулатов, новой логики, новых законов природы. Всё в микромире объясняется известными классической физике полями и законами природы, причем объясняется сугубо технически, без гипотез, без авторского вымысла и прочей фантастики. Эти ее новые начала и будут здесь изложены.

Обе "роковые" проблемы физики (размеры тел и отсутствие излучений из атомов) решаются как несложные, не требующие даже расчетов задачи по курсу теоретических основ электротехники. Все возможности для их решения имелись задолго до научной революции. Все прочие проблемы и противоречия были лишь следствиями этих двух основных. Не было перед классической физикой никогда никаких тупиков, и смена научной парадигмы не была необходимостью. Однако мнимая несостоятельность классической физики легла в фундамент всего гигантского здания современной академической физики, ее натурфилософии и мышления.

Для оценки содержания этого изложения не следует применять критерии и логику научной революции и современной физики. Здесь излагается только классическая физика в рамках своей прежней парадигмы, которая содержит собственные, отличные от современной физики логику, критерии истинности и доказательности, прежние системы исходных истин и приоритетов, прежние научную мораль, цели и т.д. Классическая парадигма не подчинена современной и не является ее частью, они антагонистичны и несовместимы, одна отвергает другую как заведомо неверную. И нельзя сказать, что классическая парадигма ниспровергнута. Ведь научная парадигма - это, по существу, технология науки или своего рода наука о том, как добывать новые знания и делать открытия. Ее эффективность оценивается не словесной критикой со стороны конкурента, а результатами, т.е. количеством и качеством открытий, влиянием науки на практику, на качества жизни человечества. При такой оценке преимущество классической парадигмы несомненно и доказано делом.

Напомню, что последнее время жизни классической школы сегодня называют веком великих научных открытий. Эта школа, малочисленная и бедная, в значительной части любительская, своими открытиями радикально улучшила жизнь человечества. И сразу же после ее великого открытия (открытия атомного ядра) была объявлена несостоятельной, т.е. не способной к открытиям (всего-то через три года, не считая лет мировой войны и революций), да еще и по причине этого открытия: именно его она якобы не объясняла (вот Вам и образец революционной логики). С ее гибелью великие открытия сошли на нет. За вторую половину ХХ века великих открытий уже не было вовсе, и современная академическая физика - целая армия профессиональных ученых и мощная индустрия науки - не внесла в нашу жизнь, в промышленность и практику ничего существенно нового, кроме лазера (транзистор изобретен еще в 1947 году). Таковы "гигантские успехи современной физики", о которых мы слышим и читаем. Она безуспешна и безнадежна, что также доказала делами. Другие же науки обошлись без революций, сохранили прежнюю парадигму, когда-то единую для всех наук, и ушли за этот срок далеко вперед. Химия обогнала физику в области сверхпроводимости, биология дала генную инженерию.

Сегодня все физики талантливы, по меньшей мере - у нас в России. Заурядных просто не принимали на физфаки уже очень много лет. Армия талантов при современном оснащении. Почему же никто их них не достиг своей мечты - великого открытия? Раньше физиками становились люди всякие, без особого отбора, и делали открытия подручными средствами. Очевидно, дело в устройстве самой науки, в ее строении, в методах, правилах, идеологии, критериях и т.д. - т.е. в ее парадигме. Сравнение результатов показывает, что классическая парадигма была вовсе не сводом устаревших догм, а мастерством великих открытий, хорошо отработанной за века и потому чрезвычайно успешной технологией науки. Век великих открытий - не сумма случайных событий, а закономерный результат этого мастерства и доказательство мощи классической парадигмы.

Напоминаю, что здесь не будет философии, только электротехника в приложении к физике. К сожалению, не умею хорошо излагать. Я наладчик, и пользуюсь здесь теорией, избегая расчетов, точно так же, как в работе на заводах, где нужны ясные и полные представления о процессах и явлениях, но редко нужны расчеты. Весь нужный для понимания теоретический материал содержится в типовом учебном курсе теоретических основ электротехники для электротехнических ВУЗов.

Классическая физика остается по-прежнему фундаментом технических наук, профессий, технологий, массового образования. Разрушение этого направления науки стало вековой преградой на пути наук и технологий в микромир, на пути технического прогресса в целом. Научная революция стала величайшим бедствием, приносящим всем и каждому, как и лично Вам, неисчислимый и всё возрастающий материальный урон, сравнимый разве что с мировой войной.

Простейшие самоорганизующиеся системы

Здесь будет описан самоорганизующийся объект, для физики новый и принципиально важный: искусственное упругое тело, состоящее из множества макроскопических элементов, расположенных на макроскопических расстояниях друг от друга и упруго связанных воедино электромагнитными полями. Объект важен по трем причинам. Во-первых, это простейший и первый пример системы, самоорганизующейся в пространстве и времени. Во-вторых, этому телу свойственны определенные размеры, оно может двигаться и претерпевать ускорения, как и тела естественные. Но здесь поля и силы, соединяющие элементы в единое тело, не скрыты в микромире, и мы впервые получаем возможность объективно рассмотреть вопросы вековой давности: как и почему зависят размеры тела от его скорости, в каком смысле и почему они постоянны? В-третьих, это единственно возможная и не описанная в литературе физическая модель твердого тела, способная существовать в реальности.

Пусть в волновое высокочастотное электромагнитное поле излучения, зависящее от координат и времени как sin(t-x) (коэффициенты будем упускать), помещен в плоскость Х и параллельно векторам электрического поля электрический осциллятор - короткий проводник с переменным электрическим током, зависящим от времени как sin(t) (той же частоты). На проводник будет действовать сила, пропорциональная произведению sin(t-x) на sin(t), что равно cos(x)/2 + cos(2t-x)/2. Второе слагаемое - быстропеременная сила, в среднем за период равная нулю и никуда проводник не движущая. Первое же слагаемое - постоянно действующая сила, движущая проводник вдоль оси Х, пока cos(x) не станет равным нулю. Она всегда стремится вернуть проводник в одну из тех точек, где cos(x)=0, двигая его в ту или другую сторону. На другом языке: осциллятор имеет дискретный ряд устойчивых положений в синхронном с ним волновом поле.

Аналогично, если через катушки нескольких электромагнитов пропускать синфазные токи сверхвысокой частоты, то магниты не только станут излучать волновое поле СВЧ, но и проявят непривычное для нас следующее свойство. Электромагниты, если находятся под действием только электромагнитных сил и начально расположены так, чтобы отталкивались друг от друга, разойдутся лишь на некоторые расстояния и будут удерживаться на этих расстояниях электромагнитными силами, как пружинами. Поскольку здесь магнитное поле - волновое, электромагниты, отталкиваясь и далее, попали бы в поле сил противоположного направления, и силы отталкивания изменились бы на силы притяжения. Поэтому они остановятся в некоторых устойчивых положениях - там, где эти силы меняют направление и равны нулю, - на некоторых устойчивых расстояниях друг от друга. При отклонении магнитов от устойчивых положений они попадут в область действия сил, возвращающих их обратно в устойчивые положения (что и позволяет применять здесь термин "устойчивые"). Если электромагниты находятся под действием только этих сил (например, свободно плавают в невесомости, в жидкости или на ее поверхности), то образуется (самоорганизуется) некое упругое тело, в какой-то степени упорядоченное по своей структуре.

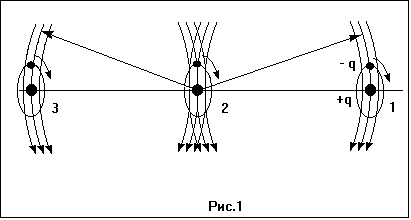
На рисунке рис.1 показана устойчивая группа из трех излучающих электрических диполей, которые равномерно и совместно вращаются вокруг общей оси (отрицательный заряд вокруг тяжелого положительно заряженного тела), и фрагменты электрических полей, излученных ранее соседними диполями. Чтобы не загромождать рисунок, показаны лишь участки электрического поля, параллельные плоскости рисунка, и лишь вблизи диполей. Диполи занимают в полях друг друга устойчивые положения, т.к. находятся в максимумах электрического поля, как в потенциальных ямах, вращаются вместе с полем, и их подвижные заряды всегда смещены вдоль поля к нижнему энергетическому уровню в нем. Будучи выведены из устойчивых положений, диполи вернутся в них или придут к новым устойчивым положениям.

Такую же способность к самоорганизации в пространстве имеют почти любые синхронные между собой источники волновых полей. Упругие связи через посредство электромагнитных волн не могут не возникать и между элементами микромира. Поля в нем достаточно сильны. Классические теории не знают других полей и сил, способных удерживать элементы на устойчивых расстояниях, поэтому нам придется признать, что в упругом теле элементы микромира выступают в качестве носителей электромагнитных колебаний и источников волн, и связаны между собой через посредство электромагнитных волновых полей.

Теперь мы знаем пример макроскопической системы, самоорганизующейся по структуре в пространстве, - группу из нескольких высокочастотных магнитов, быстро вращающихся диполей или каких-либо иных излучающих волновое поле осцилляторов, свободно плавающих в невесомости или в жидкости. Самоорганизация будет более полной, а системы - ближе к естественным, если колебания в элементах будут автономны и тоже подвержены самоорганизации, самосогласованию их по частоте и текущим фазам. Сделать такую систему для примера можно (даже в виде изделий, если очень понадобится) средствами радиотехники.

Рассмотрим систему, состоящую снова из множества одинаковых катушек, обтекаемых токами СВЧ, но пусть теперь каждая катушка будет частью автономного генератора электрических колебаний СВЧ, каждый из которых состоит из колебательного контура (конденсатора и этой катушки), усилителя, источника тока и цепи положительной обратной связи. Такие генераторы давно применяются, свойства их хорошо известны, что упрощает задачу. Пусть катушки снова служат излучателями и электромагнитами, а прочие части генераторов полей не излучают. Колебательный контур, включенный в схему генератора, - это простейший резонатор, локальная колебательная система, содержащая незатухающий колебательный процесс.

Одинаковые генераторы, будучи разрозненными, вырабатывают колебания немного неравных частот и в произвольных фазах. Находясь на некоторых умеренных расстояниях друг от друга, они взаимосвязаны через свои излучения, влияют друг на друга. Каждая катушка излучает энергию в виде электромагнитных волн и принимает энергию излучений других катушек, преобразуя ее в энергию электрических колебаний. Так колебательный процесс от каждого генератора распространяется на все другие генераторы, влияя на них. При этом генераторы, если располагаются более-менее определенным образом на некоторых расстояниях друг от друга, способны входить в синхронизм. Их колебания становятся синхронными, излучения - когерентными, а процессы колебаний и излучений сливаются в единый объемный процесс, действующий на единой частоте в едином ритме. Другими словами: происходит самоорганизация локальных колебательных процессов во времени - по частотам и фазам колебаний, сливающая волновые и колебательные процессы в единый объемный когерентный процесс.

Когда колебания в элементах системы синхронны, то сохраняется способность системы и к самоорганизации в пространстве. Элементы системы, двигаясь в волновом поле и поворачиваясь, займут в нем устойчивые положения и примут устойчивую ориентацию, образуя устойчивую пространственную структуру, в какой-то степени упорядоченную. Излучения элементов, двигаясь навстречу друг другу во всех направлениях, образуют стоячее волновое поле с узлами и пучностями, в которых и располагаются элементы.

Так мы получим систему с самоорганизацией и во времени, и в пространстве. Теперь система не связана проводами, может автономно существовать, двигаться, претерпевать ускорения.

Проще рассматривать системы, расстояния в которых достаточно велики. Тогда элементы связаны только полями излучений, но не ближними полями. Чтобы элементы пришли при этом в устойчивые положения, не разрушив синхронизм колебаний, нужно еще придать им свойство взаимного притяжения (например, придать им постоянные дипольные моменты). Генераторы остаются синхронными только на таких расстояниях, при которых происходит прием ими волновой энергии друг от друга, а это создаёт давление волн на них и силы взаимного отталкивания. Взаимное притяжение, уравновешивая давление волн, автоматически ставит элементы на расстояния, нужные для синхронизма.

Эту систему можно рассматривать также и методами электротехники как обычную электромагнитную систему с взаимной индукцией. Система в целом движется к максимуму индуктивности (это один из законов Ленца), потому катушки занимают устойчивые положения в пучностях магнитного поля системы, а магнитные потоки в этих пучностях концентрируются и становятся синфазными с магнитными полями катушек. Дополнительные силы взаимного притяжения несколько сближают катушки, вследствие чего токи взаимной индукции несколько изменяются по фазам, что делает катушки - источники энергии поля - также и приёмниками этой энергии. При этом происходит обмен энергией между элементами и частями системы, а излучение энергии в пространство может быть в ряде случаев ничтожным.

Будем считать, что размеры генераторов всегда достаточно малы в сравнении с длиной излучаемых ими волн (точечные), что массы их малы, расстояния между ними - от единиц до десятков длин волн, а число генераторов в системе достаточно велико. Конечно, мы еще не можем создать настолько малые и мощные источники излучений, чтобы образуемые ими системы были прочными, а процессы их самоорганизации в пространстве – не слишком уж медленными. Но принципиального значения это не имеет.

Простейшие резонаторы - колебательные контуры из катушек и конденсаторов - можно заменить здесь любыми другими излучающими (открытыми) резонаторами. В систему из генераторов можно включать пассивные резонаторы (без усилителей). Основные свойства системы от этого не изменятся. Но колебания должны вырабатываться в процессе автогенерации, самовоспроизводства и это здесь необходимо принципиально.

Искусственные тела можно понимать как технические устройства или приборы, предназначенные для изучения некоторых общих свойств упругих тел. Как и тела естественные, они тоже имеют размеры, к которым относится всё, что говорит современная физика о размерах тел вообще. Но отличаются тем, что созданы хорошо известными полями и силами, от которых зависят размеры этих тел, поэтому здесь размеры не могут определяться постулатом. Эти тела могут быть погружены в такие среды, где электромагнитные волны, создающие целостность тел, движутся медленнее, чем в пустоте. Длины волн и размеры стоячих полей при этом уменьшаются, потому уменьшаются расстояния между элементами и размеры тел. Приводя среду в движение относительно погруженного в нее тела, можно также наблюдать сокращение размеров. При этом можно физически или мысленно повторить эксперимент Майкельсона - Морли и убедиться, что размеры этого тела зависят от скорости относительно среды точно так же, как и длины стоячих волн рядом с этим телом.

Читая историю физики, мы узнаём, что классическая школа оказалась не способной объяснить результат этого эксперимента. Тогда физики полагали, что размеры тел определяются размерами атомов (по модели Томсона), которые, образуя тела, вплотную примыкают друг к другу. Постоянство размеров атомов, а потому – и тел, тогда казалось несомненным, что и привело к победе теории относительности над классическими представлениями. Но уже в 1911 году Резерфорд обнаружил, что размеры тел определяются устойчивыми расстояниями между атомными ядрами, относительно далеко отстоящими друг от друга. Следовательно, они зависят от свойств расстояний, от способов построения этих расстояний, от межатомных полей и сил, скрытых в микромире.

С 1911 года о постоянстве размеров судят интуитивно. Представители классической школы заявили, что размеры тел зависят от скорости, поскольку это логично. Их оппоненты, тоже не имея аргументов, назвали это смешным, нелепым, попыткой спасти теорию. Изучением свойств расстояний и способов их построения (а их не так уж и много) ни те, ни другие не занимались. Так решился самый важный во всей истории физики вопрос - о смене научной парадигмы, о дееспособности классической физики, “обычных” логики и здравого смысла. Новая физика просто перекричала старую, взяв под контроль научную печать и сделав ее рупором революции. Страсть к революции оказалась сильнее здравого смысла, логики и всей физики века великих открытий, вместе взятых. Для объективного решения нужен был, как минимум, сам объект - хотя бы один предмет, размеры которого созданы хорошо известными, не скрытыми в микромире полями и силами, и желательно – как результат самоорганизации. Но физика не обратилась ни к такой постановке вопроса, ни к поискам такого предмета, хотя все предпосылки для этого имелись: вибраторы Герца, пригодные для построения искусственных тел, были испытаны в 1888 году, а излучаемые ими поля полностью рассчитаны в 1903 году. Естественно, такие поиски были бы не в пользу научной революции.

Здесь впервые такой предмет рассмотрен, и впервые за сто лет мы получили возможность объективно изучать свойства размеров самоорганизующихся тел, движущихся произвольным образом в различных условиях – в средах и вне сред. Естественно, объект, построенный средствами классической теории, имеет свойства, не противоречащие этой теории. Однако, зависимость размеров тел (и процессов в телах) от скорости меняет классический принцип относительности движений.

Изучение свойств самоорганизующихся тел не даёт оснований для критики частной теории относительности, но позволяет понимать ее иначе - с классических позиций, как небольшой частный раздел классической теории. Несложно догадаться, что СТО фактически описывает некоторые свойства самоорганизующихся систем, и может быть понята как первая и своеобразная теория таких систем. Она принимает твердые тела - фактически гибкие самоорганизующиеся системы - в качестве меры пространства-времени, заведомо постоянной, а гибкие свойства самоорганизующейся меры относит к свойствам измеряемого объекта. Однако это мы рассмотрим в разделах 5 и 6.

Самоорганизующиеся модели упругих тел

Для того, чтобы искусственные тела могли служить достаточно полными моделями тел естественных, нужно бы решить вопрос об энергетической устойчивости таких моделей. Раньше (а может быть и поныне) физики полагали, что электромагнитные волновые поля тотчас же излучаются из микромира, в нем не задерживаются, потому не создают и силовых связей. Так и кажется на первый взгляд. Однако теоретически возможны электромагнитные динамические системы, которые содержат излучатели, но не излучают энергию в пространство. Источники волновых полей, каждый из которых излучает энергию в пространство, в принципе могут составлять систему, в пространство не излучающую, даже если находятся на расстоянии друг от друга.

Рассмотрим это сначала в общем виде. Здесь и дальше будем говорить только о периодических полях и процессах одной частоты.

Излучения двух разных источников могут в дальнем пространстве взаимно погашаться, для чего они должны быть там всюду равными и противофазными. Такое равенство возможно, в чем можно убедиться с помощью математической теории электромагнитного поля, чем и займемся. Читателю, не знакомому с этой теорией, придется пропустить три абзаца.

Всё множество возможных излучений, исходящих от источников, расположенных внутри сферы радиуса R с центром в начале координат, описывается вне этой сферы общим решением однородного волнового векторного уравнения  U + k²U = 0 в сферических координатах. Это общее решение для каждой из трех компонент вектора U может быть записано в виде двойной суммы функционального ряда, членами которого являются все частные решения U_nm = R_n(r) Ф_m( )  _nm( ) уравнения  U + k²U = 0, с неопределенными коэффициентами k_nm при них. Каждое частное решение U_nm описывает поле излучения, исходящего из начала координат, во всем пространстве, кроме начала координат, т.е. поле, излучаемое неким источником, расположенном в бесконечно малой окрестности начала координат. Решение задачи об излучении из сферы для каждого конкретного случая находят в виде суммы   k_nmU_nm , определяя коэффициенты k_nm из граничных условий на сфере или иных заданных условий.

Пусть в нашем случае некий источник излучения находится в локальной области, лежащей внутри сферы R, но на некотором отдалении от начала координат. Пусть решение для этого случая вне сферы уже найдено в виде функционального ряда с уже определенными коэффициентами k_nm. Внутри сферы этот ряд не является решением данной задачи, т.к. там есть источники поля, т.е. исходное уравнение там не однородно. Он остаётся решением однородного уравнения и внутри сферы во всех случаях, когда сходится, однако описывает излучение не данного источника, а какого-то другого, расположенного в другом месте, ближе к началу координат, например, внутри сферы меньшего радиуса. Он-то нам и нужен. Значит возможен еще один источник поля, который расположен в другом месте, на расстоянии от первого, но излучает за пределы сферы R точно такое же поле. Зная поле, можно задать для него граничные условия, т.е. систему токов на какой-либо поверхности вокруг начала координат, произвольно ее выбрав, а значит, можно построить бесконечное множество различных источников нужного нам излучения.

Нетрудно догадаться о том же, ознакомившись с теоремой единственности решения той же внешней краевой задачи. Любое из ее решений вне сферы R однозначно задаётся граничными условиями на поверхности сферы в виде произвольной функции точек поверхности. А всё множество возможных источников излучения (токов), расположенных внутри сферы, может быть описано произвольной функцией точек в объеме, т.е. множеством более высокого порядка. Проще говоря, разнообразие возможных источников поля больше, чем разнообразие возможных полей, поэтому есть бесконечное множество разных по устройству, но одинаково излучающих источников излучений. И каждая пара источников, излучающих "в бесконечность" равно и противофазно, становится неизлучающей системой. Поля вблизи этой системы могут быть неравными, тогда не погашаются, и остается ближнее поле системы, но оно не уносит энергию в пространство.

Простейшие случаи неизлучающих систем общеизвестны. Например, любой источник излучения, окруженный сплошным электропроводным экраном, не излучает во внешнее пространство. Теория объясняет это тем, что излучение источника гасится вне экрана токами, наведенными на внутреннюю поверхность экрана. В экране под действием излучения наводятся токи, чем и исчерпывается здесь роль экрана. Если экран удалить или сделать прозрачным, но сохранить наведенные токи, то излучений в пространство тоже не будет, т.е. получится не излучающий в пространство источник волнового поля. Наведенные токи и первичный источник составят систему, в пространство не излучающую. Они изучают поля, которые вне системы равны и противофазны, их векторная сумма равна нулю.

Эта неизлучающая система (как и прочие) может быть представлена как разделенная на произвольные части, каждая из которых излучает. Но при любом разделении суммарное излучение частей в дальнем пространстве равно нулю.

Конечно же, из небольшого числа простых излучателей невозможно сложить неизлучающую систему. Однако далее мы будем иметь в виду системы достаточной для этого сложности, состоящие отчасти или целиком из объёмных электромагнитных или электромеханических резонаторов, подобных, например, каплям ферромагнитной жидкости или кристаллам кварца, внутренние колебания в которых описываются уравнениями в частных производных, т.е. из резонаторов, простых по устройству, но с весьма богатыми спектрами форм резонансов и излучений.

В сложных колебательных системах, точнее, в системах с большим числом степеней свободы колебаний, возможны явления, приводящие систему к неизлучающему состоянию или к состоянию, при котором излучения из нее в некотором смысле минимальны. Рассмотрим это.

Макроскопическое тело, состоящее из множества атомов, есть сложнейшая колебательная система, которая содержит в себе множество элементов (электронов и атомных ядер, атомов в целом), несущих заряды и диполи, способных вращаться, колебаться, прецессировать и резонировать различным образом, излучая при этом электромагнитные волны. Различные сочетания и варианты всех этих потенциально возможных в системе элементарных (локальных) колебаний составят гигантское разнообразие объемных излучающих колебательных процессов. Внутренних потерь энергии в этой системе нет.

Представьте себе колебательную систему бесконечной сложности, т.е. способную содержать в своем объеме бесконечное разнообразие электромагнитных колебательных процессов (систему с бесконечным разнообразием резонансов или бесконечным числом степеней свободы колебаний на каждой частоте), в которой возможен любой колебательный процесс, о каком бы мы ни заявили, создающий любое излучение. Имеется в виду, что эти процессы не уже идут в системе, а могут быть возбуждены в ней и тогда будут продолжаться в виде свободных колебаний, пока не излучится их энергия. Из такой системы будут вообще невозможны длительные периодические излучения. И вот почему.

Если в бесконечно сложной колебательной системе без внутренних потерь энергии будет действовать какой-либо излучающий колебательный процесс, и энергия его излучений станет уходить в пространство, то в ней разовьется и другой процесс, отличный от первого, но излучающий равно с ним и в противоположной фазе, и будет гасить излучение первого. Этот второй процесс, едва зародившись и будучи как угодно малым, будет тоже излучать в пространство поле, подобное первому, но противофазное к нему, уже отчасти гася излучение первого и уменьшая мощность уходящего из системы излучения. Уменьшение уходящей мощности говорит о том, что второй процесс поглощает энергию излучений первого. Как и все колебательные процессы, он накапливает эту энергию в себе и потому усиливается. При этом два процесса обмениваются энергией через свои излучения, причем второй, слабый процесс получает энергии больше, чем отдает, он развивается до тех пор, когда излучения двух процессов сравняются, а суммарное излучение их станет нулевым. Два процесса, излучая и принимая друг от друга энергию, составят один неизлучающий процесс. Когда внутренних потерь энергии нет, такие процессы могут длиться бесконечно. Так и объясняется с точки зрения классической физики сохранение энергии движений в системах микромира.

Любое электромагнитное излучение в пространство - это векторное поле, и мощность его может быть уменьшена путем наложения на него в пространстве другого поля - с противоположным направлением векторов (так и только так происходит отбор энергии из потока излучений, иначе нарушался бы закон сохранения энергии). Тогда поток энергии будет отчасти повернут, направлен к источнику этого другого излучения, для которого станет источником энергии. Если второй источник излучения - процесс свободных колебаний, резонанс, то он, принимая энергию излучений, накапливает ее в себе в виде энергии этих же колебаний и усиливается, как бы пытаясь перехватить весь поток уходящей энергии. И это придает излучающим колебательным системам тенденцию к минимуму излучения. Если в системе окажется возможным еще один процесс, способный еще уменьшить излучение из нее, то и этот процесс будет развиваться за счет перехватываемой им из пространства энергии излучения. Так будет продолжаться или до полного погашения излучений, или до исчерпания возможностей системы (степеней свободы колебаний). Процессы складываются в один сложный процесс, не излучающий вовсе или излучающий в некотором смысле минимально. Все это происходит самопроизвольно, поэтому будем понимать это как явление самоорганизации колебательно-волновых процессов в сложных излучающих колебательных системах.

Сложность реальных макроскопических тел как колебательных систем не бесконечна, в них возможен не любой процесс, поэтому в них действуют, не затухая, лишь те процессы, которым там нашлись "антиподы" - равно и противофазно излучающие процессы. Прочие же процессы излучают свою энергию и затухают. Естественно, в системах конечной сложности спектр оставшихся процессов "дырявый" - дискретный, и чем проще система, тем меньше в ней число неизлучающих процессов, а дискретность более заметна.

В частном случае, в описанных выше системах, построенных из генераторов, тенденция к минимальному излучению колебательной энергии порождается самим принципом автогенерации, т.е. самовоспроизводства колебаний. Каждый генератор воспроизводит те колебания, которые содержатся в его колебательном контуре, независимо от их фазы. А вот количество излучаемой энергии зависит от сочетания фаз колебаний в генераторах. Ведь всё множество излучающих генераторов представляет собой некое подобие решетчатой антенны, излучение энергии из которой зависит от фазировки излучателей. Различные сочетания фаз, т.е. различные формы (или, как называют физики, "моды") колебаний и полей затухают здесь различно, а воспроизводятся в равной степени, их энергия в равной степени теряется в схемах генераторов, но в различной степени излучается. Воспроизводятся лишь те колебания, которые остались в колебательных системах, но не те, что "улетели". Поэтому, каким бы ни было начало колебаний, в итоге будет преобладать та "мода", которая излучает меньше прочих. Приток энергии в систему и амплитуды колебаний всегда чем-нибудь ограничены, поэтому в системе "выживает" лишь "мода", излучающая минимально. Она и становится устойчивой формой колебаний в этой системе.

Подобное явление имеет место во множестве сложных автоколебательных систем, и более известно в теории лазеров под названием "конкуренция мод", где оно математически описано и изучено, тенденция к минимальному излучению установлена. Систему из очень большого числа генераторов тоже можно рассматривать как некую активную (с отрицательным затуханием