Скачать

Кинетические уравнения Власова

Глава 1 Кинетические уравнения: основные понятия

1.1 Кинетические уравнения типа Больцмана

1.2 Уравнения типа Власова

Глава 2 Уравнение Власова-Максвелла, Власова-Эйнштейна и Власова-Пуассона

2.1 Сдвиг плотности вдоль траекторий динамической системы

2.2 Уравнения геодезических и эволюция функции распределения на римановом многообразии

2.3 Как ведет себя мера риманова пространства при преобразованиях

2.4 Вывод уравнения Власова-Максвелла

2.5 Схема вывода уравнения Власова-Эйнштейна

2.6 Система уравнений Власова-Пуассона для плазмы и электронов

Глава 3 Одномерная модельная задача для уравнения Власова

3.1 Условия

3.2 Постановка задачи

3.3 Математическая формализация задачи

3.4 Алгоритм разложения решения системы по параметру ε

3.5 Операторы Власова порядка n

3.6 Общая формула для поправки к полю порядка n

3.7 Классическое и релятивистское решения уравнения Власова

Заключение

Список литературы

Перечень условных сокращений и аббревиатур

ЭМП - Электромагнитное поле

Введение

Кинетические уравнения описывают эволюцию функции распределения F(t,v.x) молекул или других объектов (электронов, ионов, звезд, галактик или галактических скоплений) по скоростям v и пространству х в момент времени t. Это означает, что число частиц в элементе фазового объема dvdx есть F (t, v, x) dvdx.

Простейшее уравнение — уравнение свободного движения:

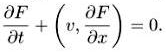                       (1.1)

Цель данной дипломной работы — рассмотреть и проанализировать основные кинетические уравнения Власова, и на их основании рассмотреть модельную одномерную задачу Коши для уравнения Власова.

Глава 1 Кинетические уравнения: основные понятия

1.1 Кинетические уравнения типа Больцмана

Первым изученным кинетическим уравнением было уравнение Больцмана. Оно учитывает процессы столкновений добавлением интеграла столкновений в (1.1):

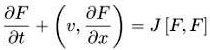                        (1.2)

Интеграл столкновений J(F,F) — это квадратичный оператор, учитывающий парные столкновения частиц. Уравнение (1.2) было получено Максвеллом и Больцманом для вывода максвелловского распределения по скоростям, которое тогда только что было использовано для объяснения закона Менделеева – Клапейрона, который будет кратко рассмотрен далее.

Максвелловское распределение связано с одним из первых успехов уравнения Больцмана (1.2) — доказательством Н - теоремы.

Теорема утверждает, что функционал

для уравнения Больцмана не возрастает: dH/dt <= 0. Этот факт был интерпретирован Больцманом как доказательство возрастания энтропии (Н есть энтропия с обратным знаком), т.е. обоснования 2-го закона термодинамики.

Неравенство Н-теоремы верно не всегда. Условие равенства нулю скорости роста энтропии даст максвелловское распределение, поэтому Н-теорема обосновывает не только стационарность максвелловского распределения, но и стремление к нему, устойчивость этого распределения, а также 2-й закон термодинамики.

Однако уравнение Больцмана писалось Максвеллом для более широких целей. Программа Максвелла состояла в том, чтобы получить уравнения сплошной среды — типа уравнений Навье-Стокса — из уравнения Больцмана и тем самым получить коэффициенты переноса — вязкости и теплопроводности — и их зависимость от межмолекулярного взаимодействия. Ему это удалось для потенциала межмолекулярного взаимодействия U(r) = r -4 (максвелловские молекулы), когда интеграл столкновений сильно упрощается. Достичь аналогичных результатов для других потенциалов не удалось ни Больцману(1), ни Гильберту. однако это сделали Чэпмсн и Энског(2) с помощью специальной схемы теории возмущений (метод Чэпмсна-Энскога). Ставки здесь были очень высоки; такое решение давало бы (и дало: оно предсказало термодиффузию) количественные предсказания в молекулярно-кинетической теории, которая в то время подвергалась критике (в полемику включились не только ученые, например Мах и Авенариус, но и политики, например В.И. Ленин «Материализм и эмпириокритицизм». Чэпмсн и Энског «немного опоздали»: определение разными независимыми способами числа Авогадро с близкими ответами убедило ученых, и страсти улеглись.

В наше время это уравнение со своими следствиями работает в нескольких направлениях. Одно из них — средние слои атмосферы. Высокие слои хорошо описываются уравнением свободного движения (1.1) — газ Кнудсена или свободный газ. Низкие слои — уравнениями газодинамики, которые выводятся из уравнения Больцмана. Сопряжение хотя бы на ЭВМ верхних и низких слоев атмосферы — одна из актуальных задач(3) в связи с летательными аппаратами. Другое направление — химическая кинетика: моделирование смесей. Со всем этим связаны дискретные модели уравнения Больцмана

Широко используемым следствием уравнения Больцмана является уравнение переноса, описывающее рассеяние частиц на заданном фоне: это линейное уравнение Больцмана. Такие уравнения используются для описания переноса нейтронов в ядерных реакторах и переноса излучения в атмосфере, когда фотоны рассеиваются средой.

Предельным случаем уравнения Больцмана служит уравнение Ландау, когда наибольший вклад вносит сильное рассеянье вперед. Оно используется для описания плазмы.

Используются также квантовые аналоги уравнения Больцмана — уравнения Улинга-Уленбека. Для этих уравнений стационарными распределениями вместо максвелловского оказываются распределения Ферми-Дирака или Бозе-Эйнштейна.

Таким образом, можно представить иерархию уравнений типа Больцмана в виде следующей схемы:

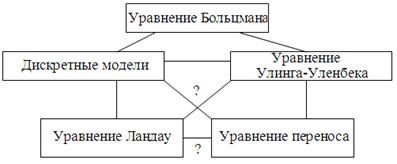
Схема 1

Линии с вопросительными знаками означают, что соответствующие уравнения еще, может быть, не выведены (например, приближение Ландау для уравнения Улинга-Уленбека).

1.2 Уравнения типа Власова

Если уравнения типа Больцмана описывают короткодействующие взаимодействия, то уравнения типа Власова описывают дальнодействие.

Уравнения Власова или уравнения самосогласованного поля имеют вид:

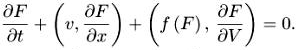                         (2.1)

Здесь сила f сама есть функционал от функции распределения, а уравнение (2.1) имеет вид уравнения сдвига вдоль характеристик. Простейший вид зависимости силы f от функции распределения соответствует парному потенциалу взаимодействия К(х, у):

                             (2.2)

Такой вид взаимодействия дает систему уравнений Власова. Обычно говорят о системах уравнений «Власова плюс ещё кого-то» для того, чтобы различать виды взаимодействий. Бывают уравнения Власова-Пуассона, Власова-Максвелла, Власова-Эйнштейна и Власова--Янга--Миллса.

Уравнение Власова-Пуассона бывает двух видов — для гравитации и для плазмы: в обоих случаях (2.2) заменяется на уравнение Пуассона действием оператора Лапласа, при условии, что К (х, у) — фундаментальное решение оператора Лапласа. Таким образом, К сеть потенциал единичного заряда в трехмерном случае, нити — в одномерном случае и плоскости — в двумерном.

Если в гравитационном случае мы заменяем взаимодействие по Ньютону на взаимодействие по Эйнштейну, то получаем уравнение Власова-Эйнштейна.

Если в случае плазмы мы заменяем электростатику на электродинамику, то получаем уравнения Власова-Максвелла. Если у нас сохраняется не заряд, а векторная величина (изотопический заряд или цвет), то вместо электромагнитных 4-иотснциалов мы должны взять матрицы, и получаем уравнения Янга-Миллса. Такие уравнения дают принятую в настоящее время теорию объединенного электрослабого и сильного взаимодействия. Таким образом, все уравнения чипа Власова дают следующую иерархию:

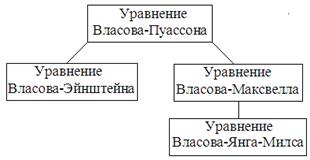
Схема 2

Данная иерархия дает нам примеры захватывающих романов между математикой и различными частями естествознания. Отдельные главы этого романа будут описаны в дальнейшем. Будут изучены следующие основные подстановки в уравнение Власова.

Уравнение динамики N тел как следствие уравнения Власова: подстановка в виде суммы дельта-функций. Подстановка в виде интегралов от дельта-функций и лагранжевы координаты. Примеры: осцилляторы и антиосцилляторы, экспоненциальное разбегание, две гамильтоновы структуры. Эйлеро—Лагранжевы координаты и гидродинамическая подстановка, N-слойная и континуум-слойная гидродинамика. Примеры: расширяющаяся Вселенная, перехлесты и границы гидродинамического описания.

Энергетическая подстановка, когда функция распределения зависит только от энергии. В этом случае уравнение (2.1) удовлетворяется, а (2.2) переходит в нелинейное уравнение для потенциала. Это уравнение аналогично уравнениям Бернулли для уравнения Эйлера. И уравнения типа Власова по своей судьбе аналогичны уравнениям Эйлера: их частные случаи стали появляться раньше, чем были написаны сами уравнения Власова. При этом в той же самой энергетической подстановке, выражающей закон сохранения энергии. В приложениях это были плазменный диод (диод Ленгмюра), уравнение Дебая для электролитов и уравнение Лэна-Эмдена в гравитации. В математике такое уравнение еще раньше было изучено в геометрии и называется уравнением Лиувилля. В двумерном случае оно имеет огромную группу симметрии (конформная группа).

Глава 2 Уравнение Власова-Максвелла, Власова-Эйнштейна и Власова-Пуассона

Вторую главу диплома хотелось бы посвятить непосредственно выводу или/и обоснованию системы уравнений Власова-Максвелла. Эта системауравнений выписана А.А. Власовым в работах(4), и широко используется для описания плазмы. Уравнения Власова—Эйнштейна обосновываются аналогично, и я только коротко остановлюсь на них. Под названием уравнений Власова-Максвелла разные исследователи понимают разные уравнения. Наиболее популярно уравнение с нерелятивистской зависимостью скорости от импульса для функции распределения. Важно связать это уравнение с классическим лагранжианом, чтобы, с одной стороны, надежно иметь «правильное» уравнение, а с другой — понимать характер сделанных приближений. Далее, при выводе уравнения Власова-Максвелла будет приведён кратчайший, видимо, путь, связывая с лагранжианом электромагнетизма. Т.к. процесс вывода уравнения Власова-Максвелла является неоднозначным, то перед этим необходимо представить вспомогательные пункты. В 2.1 будет рассмотрено как обосновываются уравнения для функции распределения частиц, сдвигаемых вдоль траекторий произвольной динамической системы хi = Xi(x). А далее изучается уравнение Эйлера-Лафанжа для случая, когда действие есть длина, а также обосновывается выбор функции распределения в переменных х, р (пространство-импульсы).

2.1 Сдвиг плотности вдоль траекторий динамической системы

Рассмотрим произвольную динамическую систему, т.е. систему нелинейных дифференциальных уравнений в k-мерном пространстве:

хi = Xi(x), i = 1,…,k                        (1.1)

Пусть мы раскидали частицы с какой-то начальной плотностью f(0, x), а в момент времени t эта плотность есть f(t, x), так что число частиц в области G

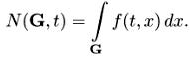
Какова эволюция f(t, x)?

Покажем, что соответствующее уравнение имеет вид (по повторяющимся верхним и нижним индексам предполагается суммирование):

                       (1.2)

Способ 1 . Метод -функций.

Рассмотрим функцию распределения N частиц, сдвигающихся по траекториям этой системы:

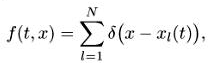
где для каждого l функция xi(t) удовлетворяет уравнениям (1.1). Тогда, дифференцируя по времени, получаем

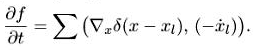
С другой стороны, имеем

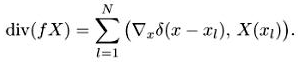
Складывая полученные выражения, находим, что уравнения (1.2) для такой функции удовлетворяются. При взятии дивергенции воспользовались формулой

Для произвольной функции f равенство (1.2) получается переходом к пределу при аппроксимации ее суммой -функций (в слабом смысле).

Способ 2 . Баланс частиц.

Скорость роста частиц в области G есть

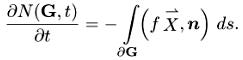                           (1.3)

Это следует из того, что на малом участке границы ds количество вылетевших за время dt частиц есть f ds dt(X,n), так как все вылетевшие частицы заметают цилиндр с основанием ds и стороной X dt, а поэтому высотой (X,п) dt. Знак минус берется потому, что нормаль — внешняя, и считаются вылетевшие частицы, тогда как слева в (1.3) стоит скорость роста числа частиц в области G. Преобразуя в правой части (1.3) интеграл из поверхностного в объемный по формуле Стокса, мы получим уравнение (1.2), проинтегрированное по области G, а отсюда в силу произвольности G — и само уравнение (1.2).

Перепишем уравнение (1.2) в виде

                  (1.4)

Если divX = 0, то левая часть (1.4) — это полная производная f(t,x) пo времени.

Вывод. Уравнение для функции распределения частиц, сдвигающихся вдоль траекторий динамической системы (1.1), имеет вид (1.2).

2.2 Уравнения геодезических и эволюция функции распределения на римановом многообразии

Рассмотрим метрику gijdxidxj в пространстве Rn, xRn, gij(x)-n2 функций. Это означает, что длина кривой определяется формулой:

                               (2.1)

а уравнение геодезических получается из принципа наименьшего действия (принципа наименьшей длины). Если, более обще, действие записывается в виде S = dt, где L—лагранжиан, то уравнения Эйлера-Лагранжа даются варьированием с фиксированными концами траекторий:

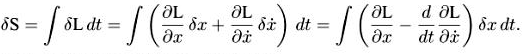
Получаем уравнения Эйлсра-Лагранжа:

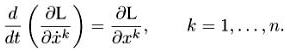
В случае геодезических L =  имеем

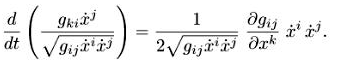                  (2.2)

Функционал длины инвариантен относительно замены t =  для любой гладкой функции , и то же свойство имеют уравнения (2.2).

Этим свойством иногда распоряжаются так, чтобы максимально упростить уравнения. Выберем(5) в качестве параметра длину линии (интервал, собственное время) s : ds =, после деления на ds получим  = 1, и уравнения (2.2) превращаются в

                                           (2.3)

Последние совпадают с уравнениями Эйлера-Лагранжа для действия с лагранжианом

Преобразуем их к виду

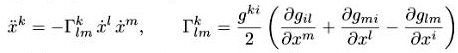            (2.4)

Здесь gki — матрица, обратная gij а  называются символами Кристоффеля.

Запишем уравнения (1.2) для функции распределения f(х, v, s) по пространству и скоростям (с длиной .s вместо времени) для уравнения (2.4), как это показано в предыдущем параграфе:

                        (2.5)

Последний член в левой части соответствует тому, что система (2.4) имеет дивергенцию, отличную от нуля. Переход к бездивергентному виду можно осуществить двумя способами.

Способ 1 . Переход к переменным координата-импульс и гамильтонов формализм.

Введем стандартным образом импульсы.(6) Если L = (gijxixj)/2 (этот лагранжиан дает те же уравнения движения, что и (2.1)), то импульсы pi = = dL/dxi= gijxj , а гамильтониан Н = pivi — L = (pipgij)/2. Тогда уравнения (2.3) приобретают гамильтонов вид

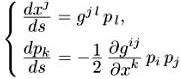
Упражнение

Показать, что для любой гамильтоновой системы дивергенция равна нулю.

Решение

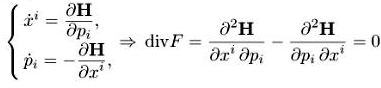
Получаем уравнения для функции распределения f(s,х,р) по координатам и импульсам (1.2) в виде

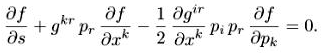                     (2.6)

Эго уравнение имеет вид

df/ds + {Н, f} = 0, где {Н, f} — скобка Пуассона:

Способ 2. Переход к инвариантной мере в пространстве координаты-скорости.

Пусть g — определитель матрицы gij. Вместо f в (2.5) введем новую функцию распределения

F{x,v,s) = F(x,v,s)/g.

Упражнение

Показать, что для новой функции распределения уравнение эволюции бездивергентно и имеет вид

Решение

Воспользуемся операцией дифференцирования определителя. При этом второе слагаемое в (2.5) преобразуется следующим образом:

В (a) используется тождество

Для новой функции распределения число частиц записывается в виде

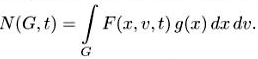
Поэтому g dxdv есть инвариантная мера: F не растет, т.е. полная производная от неё есть ноль, и поскольку число частиц сохраняется, то мера g dxdv сохраняется тоже.

Вывод. В качестве переменных в функции распределения можно брать импульсы или скорости, а в качестве времени — время или интервал s. Для простоты уравнений брали интервал, который в теории относительности называется собственным временем(7). Возможность выбрать s в качестве параметра означает синхронизацию собственного времени различных частиц. С этим связан парадокс близнецов. Тот из них, чей интервал (собственное время) меньше, т.е. который «двигался больше», оказывается младше. Поэтому использование s хотя формально и возможно, но делает затруднительным интерпретацию результатов.

2.3 Как ведет себя мера риманова пространства при преобразованиях

Пусть проведена замена координат хк = f (). Как преобразуется при этом метрика? Имеем:

Поэтому  где J — это det (дxi/д), Отсюда следует, что так как dx = |J|d, то  = , т.е. —инвариант преобразований.

Дифференцируя по параметру, имеем , а поэтому dV=|J|dv. Отсюда следует, что g dxdv =  - инвариантная мера, где каждый из сомножителей инвариантен при преобразованиях.

Вывод. В качестве переменных функции распределения удобно брать импульсы. В качестве параметра  возьмем время, в качестве переменных функции распределения — t (время), х (пространственная координата), р(импульсы): f= f(t,x,p).

2.4 Вывод уравнения Власова-Максвелла

Система уравнений Власова-Максвелла описывает движение частиц в собственном электромагнитном поле. Стартуем с обычного действия для электромагнитного поля(8), действия Власова-Максвелла или Лоренца (по повторяющимся верхним и нижним индексам идет суммирование):

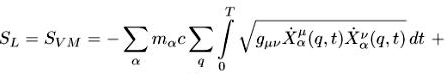
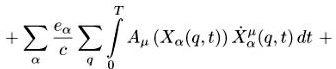                                    (4.1)

где Sр означает действие частиц (particles), Sf — действие полей (fields), Sp-f — действие частиц-полей (particles-fields).

Здесь а означает сорт частиц, отличаемый по массе mа и заряду еa, q нумерует частицы внутри сорта, (q.t) ( = 0,1.2,3; q =1,...,Na; a=1..... r) — 4 координаты q-й частицы copтa a, Au(x) — потенциал,  — электромагнитные поля,  - метрика Минковского: , т.е. диагональная матрица с 1 на первом месте и (-1) на остальных. Варьирование проводим специальным способом: сначала получаем движение частицы в поле, потом поля с заданными движениями частиц. Однако для частиц мы перейдем к функциям распределения, что и даст искомую систему уравнений.

1. Варьирование Sp + Sp+f по координатам (q.t)) даст уравнение движения зарядов в поле. Перепишем  для метрики Минковского (в дальнейшем греческие индексы ,  пробегают четыре значения:  = 0,1,2,3; латинские i,j —три: i = 1,2,3):

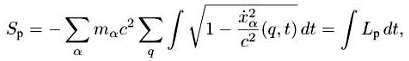
где Lp, — лагранжиан частиц.

Здесь  (i = 1,2,3) — трехмерный квадрат скорости, и мы учли, что х° = ct и вынесли с2 из-под корня. Проварьируем это выражение (опуская а):

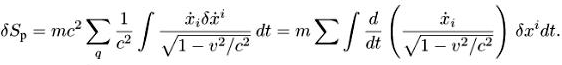
Варьируем Sp-f (снова опускаем а):

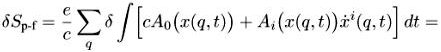
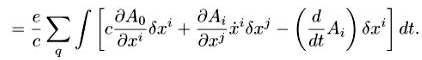
Отсюда из условия  = 0 получаем уравнение движения заряженной частицы в поле:

уравнение больцман власов динамический модельный

где

2. Уравнение для функции распределения получается как уравнение сдвига вдоль траекторий полученной динамической системы движения зарядов в поле. Видно, что удобно взять функцию распределения oт импульсов, а не от скоростей. При этом надо выразить скорости через импульсы:

Обозначая  получаем  = Отсюда находим уравнение для функции распределения fa(x,p,t) (аналог 1.4):

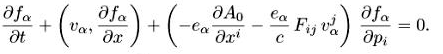               (4.2)

Здесь  Использовано, что

В это уравнение записано для ионов и электронов в следующем виде:

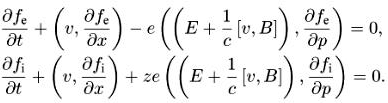                          (4.3)

Здесь fi(t, р, х) — функция распределения ионов по пространству и импульсам в момент времени t (i в (4.3) — первая буква слова ion. а не индекс), fе(t, р, х) — функция распределения электронов, ze — заряд иона, (—е) — заряд электрона, (v, B) — векторное произведение. Не выписано выражение v через р, однако часто его берут классическим: vаj = pj/ma , и тогда удобно записать уравнения через функцию распределения f(t, v, х) по скоростям вместо импульса. В записи (4.3) v надо брать различными для электронов и ионов, т.е. (4.3) требует уточнения, где vi , а где vc вместо v, и каковы эти функции, как функции импульса vi(p) и vc(p).

3. Уравнение для полей. Используем функцию распределения вместо плотности. Сначала надо переписать Sp-f через функцию распределения, совершив переход

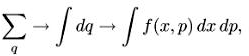
после чего Sp-f запишется в виде

Теперь варьируем по потенциалам Аu(х):

Полагаем  и получаем

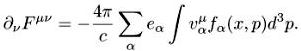                        (4.4)

Система (4.2), (4.4) и есть система уравнений Власова-Максвелла.

Замечание 1. Уравнения (4.4) являются второй парой уравнений Максвелла, а первая следует из равенств  что записывается в эквивалентном виде на языке дифференцирования кососимметрических тензоров  Первая пара уравнений Максвелла записывается в виде

Замечание 2. При выводе уравнений Власова-Максвелла по схеме Боголюбова мы должны были бы стартовать с гамильтоновых систем с потенциалами Лиенарта-Вихерта (запаздывающие потенциалы). Для слабого релятивизма соответствующий лагранжиан называется лагранжианом Дарвина.

Замечание 3. Можно таким же способом получить уравнения Вла-сова-Янга-Миллса, заменив в четырех потенциалах Au числа на матрицы.

Вывод, Система уравнений Власова-Максвелла получается при варьировании действия электромагнетизма (действия Лоренца) с переходом к функции распределения. Уравнение для функции распределения получается как уравнение сдвига вдоль траекторий движения частиц.

2.5 Схема вывода уравнения Власова-Эйнштейна

Рассмотрим действие для частицы в гравитационном поле и для поля(9):

                   (5.1)

Здесь R — кривизна; вариация но метрике производится переписыванием первого слагаемого в эйлеровых координатах:

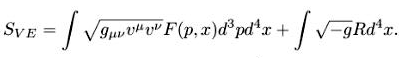 (5.2)

При этом, как и в предыдущем параграфе, получается уравнение для полей. Варьируя траектории частиц в Sp в (5.1), получаем уравнение для их движения в гравитационном поле. Уравнение для функции распределения (как и в предыдущем параграфе) сеть уравнение сдвига вдоль характеристик.

Вывод. Уравнения Власова-Максвелла и Власова-Эйнштейна получаются единообразным способом варьирования соответствующих лагранжианов электромагнетизма и гравитации.

2.6 Система уравнений Власова-Пуассона для плазмы и электронов

Рассмотрим систему уравнений Власова-Максвелла в потенциалах Аu.. Получаем волновую форму релятивистской системы уравнений Власова-Максвелла при условии дuАu = 0 (лоренцова калибровка)(10):

 (6.1)

Здесь уравнения Максвелла преобразованы по

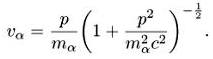
Если мы перейдем к нерелятивистскому пределу, то va = p/ma. Обычно рассматривают функцию f(t,x,v) распределения по скоростям. Получим систему уравнений Власова-Пуассона:

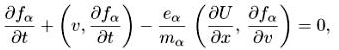
                       (6.2)

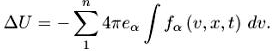
Как правило п = 1 (электронная задача) или п = 2 (плазма, состоящая из ионов и электронов).

Глава 3 Одномерная модельная задача для уравнения Власова

Рассматривается модельная одномерная задача Коши для уравнения Власова. Уравнение описывает эмиссию с бесконечной плоскости монохроматического потока электронов в самосогласованном электрическом поле. Для гладких начальных данных строится явное выражение для значения электрического поля в форме рядов Бюрмана-Лагранжа. После этого задача определения потока электронов сводится к решению линейного уравнения первого порядка по характеристикам, как в релятивистском, так и в классическом случае. Далее производится суммирование построенных рядов и распространение полученных для решения исходной задачи формул и на негладкие начальные данные (получение обобщённых решений).

3.1 Условия

Пусть радиационная генерация электромагнитного поля (далее – ЭМП) идёт в широком потоке быстрых электронов, образующемся при рассеянии в среде ионизирующих частиц. В общем случае ЭМП будет самосогласованным, то есть заметно влиять на динамику быстрых электронов, а решение подобных трёхмерных задач в сложных средах требует зачастую недоступного в настоящее время объема ресурсов ЭВМ. В ряде практически важных случаев параметры потоков ионизирующих частиц и среды оказываются такими, что эффект согласования ЭМП и плотности тока быстрых электронов невелик. Его можно попытаться учесть как малое возмущение при определении значений плотности тока и ЭМП. Другие моменты функции распределения быстрых электронов в задачах радиационной генерации ЭМП как правило интереса не представляют. Этот подход к трёхмерным задачам целесообразно исследовать в рамках более простых дву- и даже одномерных постановок при определении необходимого набора функционалов от функции распределения(11).

Условия, в которых происходит ионизирующее рассеяние, образование потоков заряженных частиц и ЭМП, создаются широким набором физических эффектов. Представляется очевидным, что все они приводят к уменьшению ЭМП и фактора самосогласования. Например, столкновения быстрых электронов со средой уменьшает их направленную скорость. В том случае, когда среда имеет исходное распределение электрофизических параметров, заметно отличающееся от вакуумного, ЭМП будет иметь заведомо меньшие значения напряженности электрического поля и магнитной индукции. То есть, адекватность методик, рассматривающих эффект согласования как малое возмущение, целесообразно исследовать в рамках модельных задач, описывающих распространение потоков электронов в вакууме.

Целью практической части работы является получение асимптотического разложения решения задачи о торможении потока электронов собственным электрическим полем в одномерной вакуумной модели и преобразование его к виду, который интерпретируется в терминах рядов Бюрмана-Лагранжа. При этом физически очевидно, что влияние поля на электроны в такой задаче заведомо завышено, что гарантирует применимость выводов о сходимости получающихся разложений к решениям для реальных моделей.

Сформулированная проблема имеет универсальный характер: анализ некоторых задач с реакторной тематикой – управление работой реактора, детальный учет эффекта выгорания и др. – приводит к необходимости рассматривать аналогичную ситуацию. Для описания поведения реактора ищется его нейтронное поле N = N(t, r, v). Такая информация, разумеется, избыточна, но с помощью неё сравнительно просто находить различные функционалы от уже найденного поля, значения которых и представляют практический интерес. В данном случае интерес представляет величина ЭМП – линейного функционала от электронного поля f = f(t, r, v), – которое само входит в систему Власова-Максвелла и, как будет рассмотрено далее, может в некоторых достаточно простых, но имеющих важные следствия, случаях быть найдено, минуя определение функции f(t, r, v), нахождение которой в дальнейшем сводится к решению классических задач с линейными уравнениями первого порядка. В этом состоит определённая специфика системы Власова-Максвелла.

3.2 Постановка задачи

Модели ЭМП в задачах его радиационной генерации строятся на основе уравнений Максвелла, содержащих роторы электрического и магнитного полей. Это связано с тем, что быстрые электроны сами ионизуют среду, порождая вторичные электроны и ионы низкой энергии. Концентрация вторичных заряженных частиц во много раз превышает концентрацию быстрых электронов. По этой причине вторичные электроны в математических моделях рассматриваются отдельно. Источником ЭМП является сторонний ток быстрых электронов и проводимость слабоионизованного газа вторичных заряженных частиц. Соответствие такой модели закону Гаусса обеспечивается уравнением непрерывности для системы всех заряженных частиц.

Рассмотрим эмиссию монохроматического потока электронов со всей плоскости xOy вдоль оси Oz в вакуум. Функция распределения электронов f(t, z, p) удовлетворяет одномерному уравнению Власова, записанному в импульсной, учитывающей релятивистские эффекты, форме:

а входящее в него E – самосогласованное электрическое поле – закону Ампера:

, .

Здесь и далее: с – скорость света; – скорость электрона; m0, re, e, – его масса покоя, классический радиус и заряд соответственно. Плоский поток заряженных частиц порождает одну компоненту плотности электрического тока j(t, z): вдоль оси Oz. В условиях такой симметрии ненулевой является только Εz-компонента ЭМП. Остальные его компоненты равны нулю вследствие уравнений Максвелла и однородных начальных данных: f(0, z, p) = 0, Ε(0, z) = 0.

Функция F(t) описывает интенсивность эмиссии с плоскости, то есть число электронов, вылетающих с единицы площади поверхности в единицу времени. Как и в реальных моделях, для неё выполнено условие F(0) = 0.

3.3 Математическая формализация задачи

В дальнейшем все функции времени предполагаются, если не оговорено противное, продолженными нулем на интервал (t < 0), а функции от r – на интервал (z < 0). Аргументы функции (или часть их) опускаются при записи, если это не приводит к недоразумению. Запись производной просто штрихом (или точкой) означает, что она взята по всему аргументу функции, а не по какой-либо его составляющей.

Задача, поставленная в предыдущем пункте, требует предварительного анализа, например, на предмет сокращения числа входящих в основные уравнения параметров – то есть, как минимум, приведения их к безразмерному виду. Проводя эту стандартную ( t= tτ, r= rρ, p= pπ, f = f ̃φ(τ, ρ, π), F = F̃Φ(τ, ρ, π), E(t, r) = EΕ(τ, ρ), J = JJ(τ, ρ), Sext = Qext/Q) операцию, видим, что между масштабными – взволнованными – коэффициентами должны иметь место стандартные же соотношения, дабы безразмерные уравнения не отличались по своей структуре от своих стартовых размерных аналогов. Таковыми являются: связь скорости и импульса (классическая или релятивистская); r = vt, причем, естественнее всегда брать c – за масштаб скоростей, а из t̃ и r̃ выбирать только одну.

В результате приходим к следующей системе соотношений, приводящих исходную систему к полностью безразмерному виду: один из параметров L = r̃, или T = t̃ является свободным, L = cT, P = p̃ = m0v0. Функции, входящие в систему, имеют своими масштабными коэффициентами следующие величины: Q̃ = 2N/(LTP), f ̃ = 2N/(LP), J̃= – |e|N/T, Ẽ = 4π|e|N, а единственный параметр, остающейся сомножителем перед Ε, – ε можно выразить как через начальные данные: ε = 4πreLN, так и через широко используемые (ωплаз)2 = 4πrec2n – плазменную частоту и νист = 1/T – частоту источника: ε = υ0(ωплаз/νист)2.

Приведенная таким образом к безразмерному виду исходная система приобретает вид:

                (1)

                                        (2)

Первой задачей анализа системы (1-2) будет получение явных формул для путём разложения его в ряд по степеням ε, что сведёт дальнейшее решение уравнения (1) к решению классического уравнения первого порядка.

3.4 Алгоритм разложения решения системы по параметру ε

Далее, на первом этапе исследования, при получении формул для E(t, z), нам потребуются производные всех порядков от временной компоненты источника F(t). Считаем, что она является действительной аналитической функцией. Зависимость v = v(p) полагаем аналитической по тем же причинам: как классическая, так и квантовая её модели, разумеется, этим свойством обладают, а для построения решения удобнее рассматривать сразу общий случай υ = υ(π) произвольного диффеоморфизма луча π > 0 на луч υ > 0 либо на интервал 0 < υ < υ0.

Поиск начального приближения  уравнения (1) приводит к формулам:

Далее, не обговаривая специально, удобно придерживаться следующих обозначений: χ = τ – ζ/υ, χ0 = τ – ζ/υ0, τ – (ζ – υ(τ – τ̃))/υ0 = χ̃0, χ̃ = χ.

Пусть . Разложив по степеням ε произведение εE φ’ и приравнивая, друг другу коэффициенты при всех последовательных степенях, получаем, как обычно, бесконечную серию уравнений, зацепленных каждое только заодно другое своими правыми частями – последовательными источниками частиц, испытавших данное число взаимодействий (соударений). Начальное уравнение цепочки (с S0 = Sext для φ0) уже выписано. Основным для дальнейшего будет то, что левая часть у всех последующих уравнений одинакова. Правые части их имеют следующий вид: . Тождественность операторов