Испытание и обеспечение надёжности ДЛА
КУРСОВАЯ РАБОТА
по дисциплине: «Испытание и обеспечение надёжности ДЛА»
Задание
Оценить надежность ДЛА по результатам огневых испытаний. Исходные данные:
Проведены огневые испытания N двигателей по программе, обеспечившей проверку всех эксплуатационных условий применения двигателя. При этом были измерены значения основного параметра - тяги двигателя R. При испытаниях зарегистрировано два отказа двигателя: один - на основном (стационарном) режиме и один – на останове. Причины отказов были установлены и устранены конструктивными изменениями, которые по своему характеру позволяют считать все испытанные двигатели за исключением аварийных, представительными для расчета надежности.
Требуется оценить надежность (вероятность безотказной работы) двигателя с учетом ограниченного объема полученной информации, выполнив расчет точечной оценки надежности ![]() и ее нижней доверительной границы
и ее нижней доверительной границы ![]() , соответствующей заданной доверительной вероятности g. При расчетах принять допущение о нормальном законе распределения тяги двигателя, обеспечив проверку правомерности такого допущения с помощью статического критерия c2.
, соответствующей заданной доверительной вероятности g. При расчетах принять допущение о нормальном законе распределения тяги двигателя, обеспечив проверку правомерности такого допущения с помощью статического критерия c2.
Общие положения, принимаемые
при оценке надежности
Представим двигатель как сложный объект, состоящий из четырех независимых систем, характеризующий следующие его свойства:
· безотказность функционирования при запуске;
· безотказность функционирования на стационарных режимах;
· безотказность функционирования на останове;
· обеспечение требуемого уровня тяги.
Принимая во внимание независимость функционирования названных систем, будем характеризовать надежность двигателя как произведение вероятностей безотказной работы отдельных его систем.
РДВ=Рзап×Рреж×Рост×Рпар, (1)
где РДВ - вероятность безотказной работы двигателя;
Рзап - вероятность безотказного функционирования двигателя на запуске;
Рреж- вероятность безотказного функционирования двигателя на стационарных режимах;
Рост- вероятность безотказного функционирования двигателя на останове;
Рпар- вероятность обеспечения требуемого уровня тяги.
В качестве величины тяги, характеризующей данный экземпляр двигателя, принимается ее среднее значение, полученное на номинальном режиме, или расчетное значение тяги, приведенное к номинальному режиму и условиям работы двигателя.
Оценка надежности двигателя осуществляется по результатам раздельной оценки надежности систем и последующего вычисления надежности двигателя в целом. При этом расчет нижней доверительной границы надежности по параметру тяги целесообразно выполнить по схеме «параметр - поле допуска», а вычисление остальных оценок надежности (точечных и интервальных) для всех систем - по схеме «успех-отказ».
Методика расчета надежности
по результатам огневых испытаний
Точечные оценки надежности систем 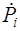 вычисляются по формуле
вычисляются по формуле
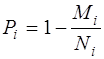 , (2)
, (2)
где Ni-общее количество испытаний i-й системы;
Mi-количество отказов i-й системы в Ni испытаниях.
Для системы обеспечения тяги в качестве числа отказов М используется число испытаний, при которых измеренные значения тяги R вышли за пределы заданного допуска (Rmin – Rmax). Измерения тяги представлены в табл. П 1 для двух базовых вариантов статистики.
Нижние доверительные границы надежности для схемы «успех - отказ» оцениваются по формуле
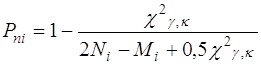 , (3)
, (3)
в которой значения c²g,k определяются по табл. П 2 в зависимости от величины доверительной вероятности g и числа степеней свободы
Ki = 2Mi+2. (4)
Для наиболее распространенного практического случая отсутствия отказов (Mi=0), имеющего место при гарантированном устранении причин всех выявленных отказов, формула (3) приобретает вид
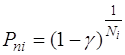 . (5)
. (5)
Так как для расчета надежности по схеме «параметр - поле допуска» требуется знание закона распределения параметра, выполним проверку справедливости предложенного выше допущения о нормальном законе распределения параметра тяги. Для этой цели используем наиболее употребительный статистический критерий c2 (критерий Пирсона), по которому за меру расхождения между статистическим (экспериментально полученным) и теоретическим законами распределения принимается величина
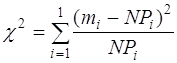 . (6)
. (6)
Здесь l- число разрядов (интервалов), на которые разбит весь диапазон возможных значений параметра; N - объем проведенных измерений; mi-количество измерений, попадающих в i-й разряд (интервал); Pi- вероятность попадания параметра в i-й интервал, вычисленная для теоретического закона распределения.
В качестве параметров теоретического нормального закона распределения принимаются величины:
· среднее измеренное значение параметра
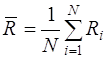 ; (7)
; (7)
· среднеквадратическое отклонение параметра, вычисленное по результатам измерений
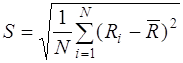 . (8)
. (8)
Полученная по формуле (6) величина c² сравнивается с некоторым критическим ее значением c²g,k, определяемым по табл. П 2 в зависимости от доверительной вероятности g и числа степеней свободы k=N-l-2. В результате сравнения правомерность принятого допущения либо подтверждается (c²
Проверка нормальности распределения осуществляется в следующем порядке:
· назначают диапазон практически возможных значений параметра, который с некоторым запасом накрывает интервал фактических измерений ( в качестве упомянутого диапазона достаточно принять интервал ![]() ± 3,5S );
± 3,5S );
· назначенный диапазон делят на 8 ÷12 интервалов, обеспечив (по возможности) удобный ряд значений, соответствующих границам интервалов;
· последовательным просмотром всех численных значений тяги относят каждое измерение к конкретному интервалу и подсчитывают количество измерений, приходящихся на каждый интервал;
· объединяют интервалы, включающие малое количество измерений, и получают окончательное количество измерений mi, попавших в каждый i-й интервал (i=1,2, ... ,l), так как первоначально выбранное количество интервалов l может сократиться до l. В нашем случае условимся объединять с соседними интервалами те из них, число измерений в которых оказалось менее четырех;
· для каждой границы i-го интервала подсчитывают значения
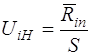 ; (9)
; (9)
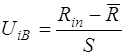 ; (10)
; (10)
при этом учитывают, что значения UiB для i-го интервала и U(i+1)Н для (i+1)-го интервала совпадают;
· находят теоретические вероятности попадания параметра в каждый i-й интервал, используя выражение:
Pi = F(UiB)- F(Uiн), (11)
в котором F(UiB) и F(Uiн) представляют собой значения нормированной функции нормального распределения (функции Лапласа), определяемые по табл. П 3 в зависимости от вычисленных значений UiB и UiH. Упомянутая таблица составлена только для положительных значений аргумента U, и в связи с этим для нахождения отрицательных аргументов целесообразно пользоваться формулой
F(-U) = 1 - F(U); (12)
· вычисляют теоретическое количество измерений параметра, попадающих в каждый i -й интервал
miтеор = Npi, (13)
при этом значения miтеор, являющиеся действительными числами, определяются с точностью до одного знака после запятой;
· находят значение критерия c² по формуле (6);
· находят критическое значение критерия c²g,k по табл. П 2 в зависимости от числа степеней свободы k = N- l -2 и доверительной вероятности g
· подтверждают справедливость принятого допущения о нормальном законе распределения параметра при выполнении условия c²
При проведении расчетов целесообразно промежуточные результаты вычислений представлять в виде таблицы, оформленной по образцу табл. 6.2. При подсчете частот попадания в каждый интервал целесообразно воспользоваться следующим приемом:
· первые четыре случая попадания в интервал отмечаются точками в графе 3 табл.6.2;
· последующие попадания в интервал отмечаются в виде тире, соединяющих отдельные точки. Законченная комбинация из четырех точек и шести тире соответствует 10-ти попаданиям. Данный прием облегчает подсчет числа попаданий в каждый интервал.
Нижнюю доверительную границу параметрической надежности находим по формуле
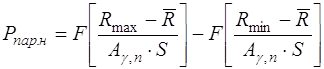 , (14)
, (14)
в которой Rmax, Rmin - максимальное и минимальное допустимые значения параметра ( верхняя и нижняя границы заданного допуска); Ag, - коэффициент ограниченности статистики испытаний, определяемый по табл. П 2 в зависимости от числа проведенных испытаний n и доверительной вероятности g.
Найденные по формулам (2), (3), (5) точечные ![]() и интервальные Рniоценки надежности отдельных систем используют для вычисления точечной и нижней доверительной границы надежности двигателя в целом по формулам
и интервальные Рniоценки надежности отдельных систем используют для вычисления точечной и нижней доверительной границы надежности двигателя в целом по формулам
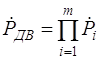 ; (15)
; (15)
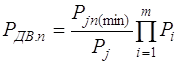 ; (16)
; (16)
в которых m - общее количество выделенных в двигателе систем; Pjn (min) - значение минимальной доверительной границы надежности (для j-й системы двигателя); Pj- соответствующая ей точечная оценка надежности.
В случае отсутствия отказов отдельных систем соотношения (15) и (16) приобретают вид
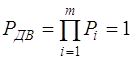 ; (17)
; (17)
РДВ.= Pin (min).(18)
Таким образом, надежность двигателя будет оцениваться минимальной нижней доверительной границей надежности Pin (min), достигнутой для отдельных систем двигателя. Эту i-ю систему следует считать лимитирующей надежность двигателя, в связи с чем дальнейшее повышение надежности РДВ следует обеспечивать мероприятиями, преследующими повышение безотказности лимитирующей системы или увеличением числа ее безотказных испытаний.
Решение
Таблица 6.1
Номер испытания | Тяга двигателя, R(m) | Номер испытания | Тяга двигателяR(m) | Номер испытания | Тяга двигателя, R(m) | Номер испытания | Тяга двигателя, R(m) |
| 1 | 82,2 | 11 | 81,69 | 21 | 81,67 | 31 | 82,91 |
| 2 | 82,6 | 12 | 81,71 | 22 | 81,9 | 32 | 82,31 |
| 3 | 80,91 | 13 | 81,38 | 23 | 82,22 | 33 | 81,97 |
| 4 | 82,69 | 14 | 81,93 | 24 | 82,1 | 34 | 82,14 |
| 5 | 82,36 | 15 | 82,24 | 25 | 81,82 | 35 | 82,15 |
| 6 | 82,53 | 16 | 83,47 | 26 | 82,27 | 36 | 82,45 |
| 7 | 82,09 | 17 | 81,76 | 27 | 80,63 | 37 | 81,73 |
| 8 | 81,54 | 18 | 81,29 | 28 | 82,19 | 38 | 83,18 |
| 9 | 81,54 | 19 | 81,87 | 29 | 81,44 | 39 | 81,88 |
| 10 | 81,2 | 20 | 82,8 | 30 | 81,12 |
· безотказность функционирования на запуске;
· безотказность функционирования на стационарных режимах;
· безотказность функционирования на останове;
· безотказность обеспечения требуемого уровня тяги.
Надежность двигателя РДВ будет оцениваться как произведение надежностей отдельных систем в соответствии с формулой (1).
Для вычисления точечных оценок надежности используем общую формулу
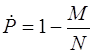 , (19)
, (19)
где М число отказов в Nиспытаниях.
В нашем случае число отказов на запуске, режиме и останове равно нулю (отказы признаны незачетными в связи с гарантированным устранением их причин), отказов по параметру тяги не зарегистрировано (все измеренные значения тяги находятся в интервале допустимых значений). Следовательно,
![]() зап = 1,
зап = 1, ![]() реж = 1,
реж = 1, ![]() ост = 1,
ост = 1, ![]() пар = 1,
пар = 1, ![]() ДВ = 1. (20)
ДВ = 1. (20)
Для нахождения нижних доверительных границ надежности
систем воспользуемся общей формулой
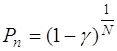 , (21)
, (21)
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Техника СВЧ
- Разработка блока управления электромеханическим замком
Конструирование РЭС - сложный творческий процесс, не имеющий пока строгой всеохватывающей математической базы и ведущийся методом мног
- Международное сотрудничество в освоении космического пространства
В своей работе я хочу рассмотреть тему «Международного сотрудничества в освоении космического пространства» и более детально узнать е
- Разработка для контроля и определения типа логических интегральных микросхем методом сигнатурного анализа
Заводы и предприятия, выпускающие радиодетали (и в частности - микросхемы), после изготовления, но до отправки готовой продукции на склад
- Разработка макета системы персонального вызова
РЕФЕРАТ Пояснительная записка к дипломному пpоекту "Разpаботка макета системы персонального вызова" содеpжит листов , иллюстpаций , табл
- Разработка методики программного тестирования цифровых устройств с помощью программного пакета Design Center
- Спутниковые системы местоопределения
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

