Скачать

Использование измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии

ДИПЛОМНАЯ РАБОТА

ИСПОЛЬЗОВАНИЕ ИЗМЕРЕНИЙ И РЕШЕНИЕ ЗАДАЧ НА МЕСТНОСТИ ПРИ ИЗУЧЕНИИ НЕКОТОРЫХ ТЕМ ШКОЛЬНОГО КУРСА ГЕОМЕТРИИ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ . . . . . . . . . . 3

ГЛАВА 1. Содержание и методические особенности проведения факультатива

§1. Простейшая геометрия на местности . . . . . 5

§2.Измерения при различных ограничениях . . . 11

§3.Преподавание математики в сельской школе. . . 12

§4. Факультатив, как одна из форм проведения внеклассной

работы по геометрии . . . . . . . 15

§5. Методика проведения факультативных занятий по теме «Решение

задач на местности» . . . . . . . 16

§6. Педагогический эксперимент . . . . . 30

ГЛАВА 2. Комплекс задач, решаемых на местности

§1. Задачи с измерениями при различных ограничениях . 33

§2. На равном расстоянии . . . . . . 39

§3. Задачи, предлагаемые учащимся сельской школы . 47

ЗАКЛЮЧЕНИЕ . . . . . . . . . 62

ЛИТЕРАТУРА . . . . . . . . . 64

Введение

Пусть читатель прогуливается в огромном

саду геометрии, в котором он сможет подобрать

себе такой букет, какой ему нравится.

Давид Гильберт.

Одной из самых важных проблем сегодня в нашей стране является проблема образования. Причем речь идет не о высшей ступени, а о средней, самой главной, ступени образования. Сущность проблемы заключается в том, что у учащихся снизился интерес к изучению, как всех предметов, так и математики, в частности. Поэтому цель работы состоит в повышении интереса к математике за счет изучения нового, не связанного с общеобразовательной программой материала.

В наше время происходят процессы глобализации образования, широкого внедрения новых технологий дистанционного обучения, Интернет и мультимедиа-технологий. Необходимо видеть, что наряду с несомненными достоинствами происходящие процессы несут в себе и отрицательные моменты. Технологизация, компьютеризация образования удаляет ученика от учителя других учеников. Одним из возможных направлений сближения может быть повышение интереса к предмету, демонстрация его практических приложений, возможность решать интересные и практически значимые задачи вместе (как с учителем, так и с группой учеников). Особенностью большинства задач на местности является то, что для получения данных задачи и ее решения необходимо участие нескольких человек.

Образование теснейшим образом связано с духовной культурой. Цель всего образования и математического образования в частности – формирование, воспитание духовной культуры личности. Геометрическое мышление в своей основе является разновидностью образного, чувственного мышления.

Наглядность и практичность обучения геометрии являются необходимыми условиями успешного ее изучения. Формирование отвлеченного мышления у школьников с первых школьных шагов требует предварительного пополнения их сознания конкретными представлениями. При этом удачное и умелое применение наглядности побуждает учеников к познавательной самостоятельности и повышает их интерес к предмету, является важнейшим условием успеха (7).

Наглядные методы применяются на всех этапах педагогического процесса. Формирование геометрических представлений является важным разделом умственного воспитания, политехнического образования, имеют широкое значение во всей познавательной деятельности человека (13) .

Известно, что механическое, нетворческое усвоение школьниками большого объема фактов, представленных в школьном курсе математики, несовместимо с подлинной образованностью, с полноценным воспитанием умственных, нравственных и других качеств личности учащихся, подготовкой их к активному участию в создании материальных и духовных ценностей независимо от того, какую профессию они получат в дальнейшем. Удачный подбор содержательных практических задач еще не обеспечивает должного эффекта. Такие задачи, как правило, вызывают у учащихся затруднения. Условия прикладной задачи только тогда легко доходит до сознания учащихся, когда они (а тем более учитель) встречались с описываемой производственной ситуацией в реальной действительности. Поэтому при постановке задач следует широко опираться на наглядные аналоги из производственного окружения школы, на трудовой опыт учащихся.

Велико значение геометрии в развитии личности. Установлено, что развитое пространственное мышление, прочные математические знания и умения школьников представляют собой важнейшие компоненты готовности к непрерывному образованию, что является актуальным в настоящее время. Необходимость достаточно высокого уровня развития пространственного мышления для успешного усвоения учащимися общеобразовательных предметов и дальнейшего профессионального образования в условиях современного производства доказана многими исследователями психологами.

Умение решать задачи на местности – так же как и руководить их решением – приходит с опытом, при систематическом использовании таких задач в учебном процессе.

Все выше сказанной говорит об актуальности проблемы исследования, которая заключается в изучении теории и отборе содержания данной темы для школьного курса математики.

Объектом исследования является процесс обучения учащихся математике.

Предметом исследования – содержание темы «Использование измерений и решение задач на местности при изучении школьного курса геометрии» и организация деятельности учителя и учащихся.

Задачи исследования:

1. Изучить математическую, психолого-педагогическую, методическую литературу по проблеме исследования.

2. Подобрать и адаптировать для школьников теоретический и практический материал, позволяющий продемонстрировать приложение геометрических фактов к решению задач на местности.

3. Найти эффективные пути и способы организации факультативных занятий.

4. Разработать методику проведения факультативных занятий по теме «Решение задач на местности».

5. Провести экспериментальную проверку отобранного материала и методики факультативных занятий.

ГЛАВА 1

§1. Простейшая геометрия на местности

Для практических целей часто возникает необходимость производить геометрические построения на местности. Такие построения нужны и при строительстве зданий, и при прокладке дорог, и при различных измерениях объектов на местности. Можно подумать, что работа на ровной поверхности земли (а именно такой мы и будем ее считать во всех задачах настоящего параграфа) ничем, по существу, не отличается от работы циркулем и линейкой на обыкновенном листе бумаги. Это не совсем так. Ведь на бумаге циркулем мы можем проводить любые окружности или их дуги, а линейкой — любые прямые. На местности же, где расстояния между точками довольно велики, для подобных действий понадобилась бы длинная веревка или огромная линейка, которые не всегда имеются под руками. Да и вообще чертить прямо на земли, какие бы то ни было линии—дуги или прямые — представляется весьма затруднительным. Таким образом, построения на местности имеют свою специфику (21).

Необходимо отказаться от проведения настоящих прямых на земле. Будем эти прямые прокладывать, т. е. отмечать на них, например, колышками, достаточно густую сеть точек. Для практических нужд этого обычно хватает, поскольку передвижение по прямой от одного колышка к другому, расположенному на близком расстоянии от первого, - действие, вполне осуществимое.

Так же необходимо при построениях не проводить на земле какие-либо дуги вообще — большие или маленькие. Поэтому фактически циркуля у нас нет. Все, что остается от циркуля,— это способность откладывать на данных (проложенных) прямых конкретные расстояния, которые должны быть заданы не численно, а с помощью двух точек, уже обозначенных колышками где-то на местности. Ведь сами расстояния будут измеряться шагами, ступнями, пальцами рук или любыми подходящими для этой цели предметами (в лучшем случае измерительными приборами). Так что отложить расстояние, составленное, скажем, из 25 шагов, 3 размахов пальцев и 2 спичечных коробок, можно лишь в таком же виде, но никак не умноженное, к примеру, на или на .

При указанных ограничениях, не пользуясь к тому же транспортиром, работать, конечно, трудно, но все же задачи решаемы.

На местности колышками обозначены две удаленные друг от друга точки. Как проложить через них прямую и, в частности, как можно без помощника устанавливать колышки на прямой между данными точками? (6)

Пользуясь зрительным эффектом состоящим в загораживании двух колышков третьим, стоящим на общей с ними прямой, нетрудно установить еще один колышек в некоторой точке С на продолжении отрезка с концами в двух данных точках А и В. После этого точки отрезка АВ можно построить с помощью того же эффекта, поскольку они будут лежать на продолжении либо отрезка АС, либо ВС (в зависимости от того, какая из точек — А или В — находится ближе к течке С). Вообще, любая точка прямой АВ будет лежать на продолжении хотя бы одного из отрезков АВ, АС или ВС.

На местности колышками обозначены две точки одной прямой и две точки другой прямой. Как найти точку пересечения этих прямых?

Пользуясь зрительным эффектом, указанным в
решении задачи выше, легко найти точку пересечения прямых в том случае, если сразу ясно, что она лежит на продолжениях обоих отрезков с концами в данных точках. В противном случае достаточно сначала проложить одну или обе прямые так, чтобы на каждой из них с одной стороны от предполагаемой точки пересечения были отмечены по две точки.

На местности обозначены точки А и В. Найдите точку С, симметричную точке А относительно точки В.

Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится измерить в подходящих единицах длины расстояние между точками А и В.

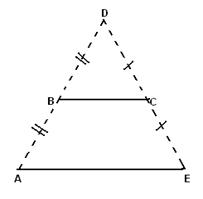
Рис. 1

На местности обозначены три данные точки А, В и С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную прямой ВС.

Продолжим прямую АВ за точку В и отложим на ней точку Dна расстоянии АВ от точки В (рис. 1). Продолжим прямую CDза точку С и отложим на ней точку Е на расстоянии CDот точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника ADE. Предложенный способ выгодно отличается от множества других способов, опирающихся па измерение углов или на деление отрезка пополам.

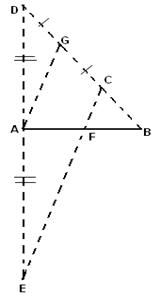
Рис. 2

Найти середину отрезка АВ, заданного на местности двумя точками А и В.

Возьмем какую-либо точку С, не лежащую на прямой АВ. Продолжим прямую ВС за точку С и отложим на ней точку Dна расстоянии 2ВС от точки С (рис. 2). Продолжим прямую ADза точку А и отложим на ней точку Е на расстоянии ADот точки А. Искомая середина Fотрезка АВ лежит на его пересечении с прямой ЕС. Действительно, отрезок СЕ параллелен отрезку AG— средней линии треугольника CDE(здесь G— середина отрезка CD). Так как, кроме того, BC=CG, то CF— средняя линия треугольника ABG, откуда AF=FB.

Быть может, приведенный способ нахождения середины отрезка покажется не самым простым. Однако его преимущества хорошо проявляются в следующей задаче, решив которую ученик сможет делить отрезок не только на две, но и на любое число равных частей.

Отрезок, заданный на местности двумя точками А и В, требуется разделить в отношении, в котором находятся длины двух отрезков KLи MN, заданных на местности точками K, Lи М, N. Как это сделать?

Построение точки F, делящей отрезок АВ в отношении AB:BF=KL:MN, произведем аналогично построению середины отрезка АВ , описанному в решении задачи 1.5. Отличие будет состоять только в том, что точку С выберем на расстоянии KLот точки В, а точку D – на расстоянии 2MN от точки С (рис.2). В этом случае прямая ЕС по-прежнему будет параллельна отрезку AG, а значит, разделит отрезок АВ в том же отношении, в котором она делит отрезок BG.

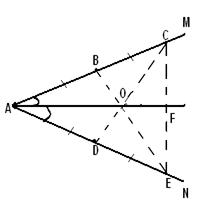
Рис. 3

На местности обозначены три точки А, М и N, не лежащие на одной прямой. Проложить биссектрису угла MAN?

Выберем на одной стороне данного угла (рис. 3) точки В и С, а на другой точки Dи Е так, чтобы выполнялись равенства

AB=ВС=АD=DE

Найдем точку О пересечения прямых BEи CD. Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике АСЕ биссектриса AFявляется одновременно и медианой, а значит, проходит через точку О пересечения медиан ЕВ и CD.

Проложите на местности какую-нибудь прямую, перпендикулярную прямой, проходящей через заданные точки А и В. Как проложить перпендикуляр к прямой АВ, проходящий через данную точку Н?

Продолжим прямую АВ за точку В и отложим на ней точку С на расстоянии АВ от точки В. Кроме того, отложим на том же расстоянии от точки В еще две точки Dи Е в двух разных, но не противоположных направлениях (рис. 4). Найдем точку Fпересечения прямых АЕ и CD, а также точку Gпересечения прямых ADи СЕ.

Прямая FGперпендикулярна прямой АВ. Действительно, точки А, Е, Dи С равноудалены от точки В, т.е. лежат на одной окружности с центром В и диаметром АС. Следовательно, вписанные углы ADCи АЕС прямые, поэтому ADи СЕ — высоты треугольника AFC. Так как все три высоты этого треугольника пересекаются в одной точке G, то прямая FGперпендикулярна стороне АС. Для того чтобы проложить перпендикуляр к прямой АВ через данную точку Н, достаточно проложить через эту точку прямую, параллельную прямой FG.

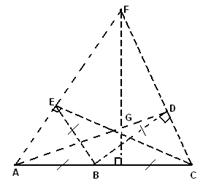
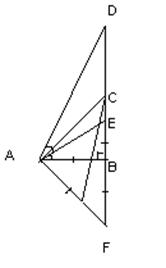
Рис. 4 Рис. 5

На местности обозначены точки А и В. Найдите точки С, Dи Е, для которых выполнены равенства =45є, є , є.

Проложим перпендикуляр к прямой АВ, пересекающий в какой-то точке луч АВ. Без ограничения общности считаем для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложим точки С и F(рис. 5), удаленные от точи В на расстояние АВ. Тогда угол ВАС равен (из равнобедренного прямоугольного треугольника ABC). На прямой AFотложим точку Gна расстоянии АВ от точки А, затем на прямой ВС отложим точку Dна расстоянии СО от точки В. Тогда угол BADравен 60°, так как по теореме Пифагора для прямоугольных треугольников ABC, ACGи АВDимеют место равенства

AD=.

Для построения точки Е теперь остается проложить биссектрису угла ВАD.

§2.Измерения при различных ограничениях

Для нахождения расстояний, высот, глубин или других размеров реальных объектов не всегда можно обойтись непосредственным их измерением — во многих случаях такие измерения сопряжены с определенными трудностями, а то и вообще практически невозможны (5). Однако в своей деятельности человеку приходится порой задумываться над тем, как все-таки можно определить интересующую его величину и как сделать это поточнее.

Основными измерительными «приборами», которые всегда имеются «под рукой», являются: шаг, пядь (размах пальцев), сажень (размах рук), уровень глаз (расстояние от земли до глаз) и т. д. Не менее важно следить за надежностью способа, т.е. зависимостью его точности от различных погрешностей, которые неизбежно возникают при работе на местности (11).

Определить длину своего шага, чтобы впоследствии измерять расстояния шагами достаточно легко. Самый простой и, казалось бы, точный способ состоит в том, чтобы сделать один шаг и измерить расстояние между крайними (наиболее удаленными) точками двух ступней. Такой способ явно не годится по двум причинам. Во-первых, расстояние между крайними точками ступней не равно длине шага, а превосходит ее на длину одной ступни (правильнее было бы измерить расстояние, например, между носками двух ступней). Во-вторых, при всем старании вряд ли можно сделать один обычный шаг — для этого вам нужно оказаться в состоянии обычной ходьбы.

Для определения длины шага достаточно пройти какое-либо заранее известное и не слишком короткое расстояние, скажем между соседними километровыми или стометровыми столбиками на шоссе, и поделить это расстояние на количество сделанных шагов.

Отметим, что средняя длина шага взрослого человека примерно равна половине его роста, считая до уровня глаз.

Измеряя какие-либо длины пальцами руки, лучше не отрывать руку от измеряемой поверхности, а приставлять один палец к другому, который затем снова вытягивать в заданном направлении (описанный процесс отдаленно напоминает движение гусеницы). Чтобы найти длину такого размаха своих пальцев, проще всего отложить вдоль какой-нибудь прямой одни или несколько десятков размахов пальцев, а затем поделить на их количество отложенную в результате длину.

§ 3.Преподавание математики в сельской школе

В особое внимание нуждается сельская школа. Ее состояние и уровень работы существенно влияет на социальное развитие села, закрепление молодежи, повышение культурного уровня сельского населения, решение демографических проблем в деревни. Перед сельской школой ставится задача воспитания у учащихся стремления активно участвовать в подъеме сельскохозяйственного производства (19).

Большие возможности естественной органической связи учебного материала с сельскохозяйственным производством имеются у учителя математики. Такая связь может осуществляться различными способами: сообщение учителя на уроках о применении изучаемых вопросов в сельскохозяйственной практике, решение задач прикладного характера, проведение практических работ и экскурсий.

Традиционной и наиболее естественной формой связи учебной работы по математике с сельскохозяйственным производством является решение на уроках задач из сельскохозяйственной практики. С другой стороны, практические задачи способствуют формированию правильного понимания природы математики, развитию материалистического мировоззрения.

Свойства измерения отрезков находят применение на практике. Рассмотрим инструмент (демонстрирует модель—см рис 6,а), с помощью которого удобно производить проверку глубины вспашки. Называется инструмент бороздомером. Он состоит из двух линеек одинаковой длины неподвижной, оканчивающейся угольником, и подвижной. Для замера глубины пахоты бороздомер устанавливают вертикально угольником на непаханую поверхность поля, а подвижную линейку опускают на расчищенное дно борозды Верхний конец подвижной линейки показывает глубину борозды по шкале, нанесенной от верхнею конца неподвижной линейки. Докажем это.