Ионометрия и электродинамика
Немировский А.М.
Глубокое знакомство с литературными источниками, посвященными ионометрии, выявляет фатальную склонность авторов использовать закон Нернста для объяснения абсолютно всех явлений ионометрического эксперимента. Упоминание о законе считается почти правилом хорошего тона. Однако хорошие манеры в некоторых случаях не могут исправно объяснять наблюдаемые эффекты. В связи с этим меня заинтересовала проблема взаимодействия законов ионометрии и электродинамики. На мой взгляд, ионометристы пренебрегают законами электродинамики, углубляясь только в химическую сторону дела.
Рассмотрим следующий пример. Допустим, что нам предстоит работать с нитратным ионоселективным электродом на ПВХ-матрице. Однако нам стало известно, что среда, в которой предстоит делать измерения, взаимодействует с пластификатором мембраны, внося свой вклад в общий потенциал электрода. Как быть? Надеяться на то, что можно описать такую систему с помощью уравнения Никольского не приходится, так как электродноактивное вещество и пластификатор вряд ли связаны химическим массообменом. С другой стороны, нет повода считать, что потенциалы от потенциалопределяющего иона и пластификатора просто складываются.
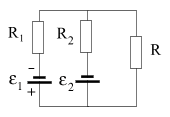
Для случаев такого рода я предлагаю модель параллельно соединенных источников э.д.с. В этой модели часть потенциалопределяющих реакций рассматриваются в виде источников э.д.с. в том виде, как это принято в электродинамике:
где
e 1 - э.д.с. источника тока, организованного потенциалопределяющим ионом;
e 2 - э.д.с. источника тока, организованного альтернативной электрохимической реакцией;
R1 и R2 - внутренние сопротивления источников тока;
R - сопротивление измерительного прибора.
Используя правила Кирхгофа для расчетов в замкнутых электрических цепях, получим следующую систему уравнений:
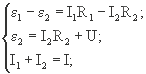
где I - сила тока на участке цепи с сопротивлением R.
Если R>>R1+R2, то измеряемое прибором напряжение равно
![]()
Так как мы договорились о том, что e 1 вызывается потенциалопределяющим ионом, то
![]()
или
![]()
Из этого следует, что потенциал (э.д.с.) параллельной реакции уменьшает наклон электродной функции (S) при условии, что этот потенциал не зависит от концентрации потенциалопределяющего иона! Тому есть экспериментальные подтверждения, достаточно вспомнить нитратселективные электроды на основе четвертичных аммониевых солей, хлоридные электроды на основе смеси сульфидов и хлоридов серебра и т.д.
Развивая гипотезу о параллельных электродинамических процессах, рассмотрим другой пример. Допустим, что анализируемый раствор состоит из смеси солей основного и мешающего ионов, причем механизмы потенциалобразования этих ионов различны. (Представить такое сложно, но можно.) Тогда
![]()
где B1 и B2 - константы,
Этот пример интересен тем, что если строить калибровку по основному иону в растворе мешающего, то это никак не будет влиять на линейность калибровки. Кроме того, приведенный пример допускает существование таких электрохимических систем, в которых влияние мешающего иона в большей мере сказывается на абсолютном значении потенциала, нежели на наклоне электродной функции. Это является очень важным аналитическим фактом, расширяющим возможности метода добавок. (Как известно, в методе добавок малое влияние мешающих ионов на наклон электродной функции является очень важным.) Не нужно говорить о том, что классическая модель (уравнение Никольского) не предполагает таких вариантов, так как мешающий ион влияет на результаты анализа следующим образом:
U = const + S * lg ( C + KCm ),
где С и Сm - концентрации основного и мешающего ионов;
К - коэффициент селективности.
Однако гипотезы гипотезами, но существуют ли приметы, подтверждающие правильность приведенных выше рассуждений? Кроме того, правомерно ли использовать правила Кирхгофа для реальных химических источников электричества.
Сразу же скажу о том, что мною были проведены опыты на батарейках фирмы "TOSHIBA". Измерение напряжения параллельно соединенных батареек показало, что правила Кирхгофа справедливы. В таблице приведены результаты проведенных опытов.
R1, МОм | R2, МОм | e 1, В | e 2, В | U, В | Uтеорич.,В |
| 8,09 | 8,17 | 1624,5 | 1614,4 | 1619,4 | 1619,5 |
| 1624,5 | 3274,3 | 2445 | 2445,3 | ||
| 1624,5 | 4898,7 | 3252,9 | 3253,5 | ||
| 3,33 | 8,17 | 1624,1 | 1614,3 | 1621,1 | 1621,3 |
| 1624,1 | 3274,2 | 2101,1 | 2101,9 | ||
| 1624,1 | 4898,7 | 2570,7 | 2572,3 | ||
| 0,942 | 0,788 | 1619,4 | 1658,6 | 1641,2 | 1640,7 |
| 1619,4 | 3282,8 | 2526,1 | 2525,1 | ||
| 1619,4 | 4906,6 | 3410,9 | 3409,3 | ||
| 0,01067 | 0,0952 | 1588,1 | 1655,1 | 1594,8 | 1594,9 |
| 1588,1 | 3275,9 | 1759,5 | 1758,2 | ||
| 1588,1 | 4898,6 | 1924,1 | 1921,7 |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Ионометрическое определение хлоридов в растворах хроматов
Немировский А.М.Задача определения хлоридов в хроматных растворах пришла от гальваников. Дело в том, что в травильных ваннах необходим
- Химический метод Винклера для определения растворенного кислорода
Каверин А.В.Среди методов определения концентрации растворенного кислорода самым старым, но до сих пор не потерявшим своей актуальнос
- Химико-аналитические свойства ионов d-элементов
Ионы d-элементов 1В группыРеакции обнаружения ионов меди Сu2+Действие группового реагента H2S. Сероводород образует в подкисленных раств
- Угарный газ
Физические свойства.Монооксид углерода представляет собой бесцветный и не имеющий запаха газ, малорастворимый в воде.t пл. 205 °С, t кип.
- Полярографическое определение цинка в присутствии меди
- Экзамен по химии за 11 класс
1999-2000 г.Вопросы экзаменационных билетов По курсу химии средней (полной) школы предлагает два блока экзаменационных билетов: для общеоб
- Химико-аналитические свойства ионов p-элементов
Ионы р-элементов IIIА группыРеакции обнаружения ионов алюминия Al3+Действие группового реагента (NH4)2S. Из водного раствора сульфид аммони
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

