referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Интерпретация фотоэффекта
Филипп Канарёв
Наиболее приемлемая интерпретация экспериментальных зависимостей фотоэффекта была предложена А. Эйнштейном в 1905 году, за что он получил Нобелевскую премию (1), (2), (3). Он сделал это в отсутствии закона формирования спектров атомов и ионов. Теперь этот закон открыт, и мы можем проверить правильность его интерпретации и возможность более глубокого понимания фотоэффекта (4), (5), (6), (7).
Математическая модель, предложенная А. Эйнштейном для интерпретации экспериментальных зависимостей фотоэффекта, имеет вид (3):
Ek = hν – W, | (1) |
где Ek – кинетическая энергия фотоэлектрона, испускаемого фотокатодом; hν – энергия фотона, но какого именно, в работах (1), (2), (3) не поясняется; W – работа выхода фотоэлектрона представляет собой константу, не зависящую от частоты (1), (2), (3).
Экспериментальные зависимости фотоэффекта представлены на рис. 1 (2).
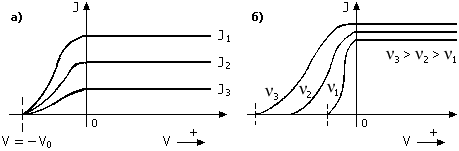
Рис. 1. Зависимость фототока от интенсивности света: а) при постоянной его частоте; б) при разной частоте
Фототок возникает в цепи: фотокатод – коллектор. Если фотокатод облучать монохроматическим светом (рис. 1а), то величина потенциала –V, задерживающего фотоэлектроны, выходящие из фотокатода, не зависит от интенсивности света. При этом увеличение интенсивности света увеличивает фототок и не изменяет величину задерживающего потенциала, а значит и кинетическую энергию фотоэлектронов. При увеличении частоты света, падающего на фотокатод, величина отрицательного потенциала V, задерживающего фотоэлектроны, увеличивается (рис. 1б).
Поскольку величина задерживающего отрицательного потенциала V определяется кинетической энергией Ek электронов, излучаемых фотокатодом под действием светового облучения, то из зависимости, показанной на рис. 1б, следует, что при увеличении частоты фотонов, облучающих фотокатод, кинетическая энергия Ek испускаемых им фотоэлектронов увеличивается.
Попытаемся найти связь уравнения (1) А. Эйнштейна с математической моделью закона формирования спектров атомов и ионов (2). Нами уже показано, что математическая модель, описывающая спектры многоэлектронных атомов и ионов, имеет вид (4), (10), (12):
Eph = Ei – E1/n2, | (2) |
где Eph – энергия фотона, поглощаемого или излучаемого электроном; Ei – энергия ионизации электрона; E1 – энергия связи электрона с ядром атома, соответствующая его первому энергетическому уровню; n = 2, 3, 4 – главное квантовое число.
Соотношение (2) следует из экспериментальной спектроскопии, поэтому оно является математической моделью закона формирования спектров атомов и ионов. Эйнштейновское уравнение (1) также описывает аналогичный процесс поглощения фотонов электронами. Это дает нам основание предположить идентичность уравнений (1) и (2) и однозначность их интерпретации. Действительно, из приведенных уравнений следует
Ek = Eph. | (3) |
Это значит, что если электрон теряет связь с ядром атома, то его кинетическая энергия Ek оказывается равной энергии Eph поглощенного фотона. Далее
hν = Ei. | (4) |
Из этого явно следует, что величина энергии hν в уравнении (1) является энергией ионизации Ei электрона, излучаемого материалом фотокатода. Из уравнений (1) и (2) также следует
W = E1/n2 = Eb. | (5) |
Новое прояснение: работа выхода фотоэлектрона W равна энергии связи электрона E1/n2 в момент пребывания его на определенном энергетическом уровне в атоме или молекуле.
Экспериментальные исследования фотоэффекта обычно проводят с фотокатодами из щелочных металлов (1). Например, известно что, работа выхода фотоэлектрона с литиевого фотокатода равна W = 2,4 эВ (1). Энергия ионизации этого электрона равна Ei = 5,392 эВ, а энергия связи его с ядром, соответствующая первому энергетическому уровню, – E1 = 14,05 эВ (4). Учитывая это, и используя математическую модель закона формирования спектров атомов и ионов (2), получим теоретический спектр этого электрона Eph (теор.), который полностью совпадает с экспериментальным Eph (эксп.) спектром (табл. 1). При этом формула (5) позволяет рассчитать энергии Eb связи этого электрона с ядром атома (по Эйнштейну работу выхода), соответствующие всем (n) энергетическим уровням этого электрона (4).
Таблица 1
Спектр первого электрона атома лития, эВ
| Значения | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 |
Eph (эксп.) | – | 3,83 | 4,52 | 4,84 | 5,01 |
Eph (теор.) | 1,88 | 3,83 | 4,51 | 4,83 | 5,00 |
Eb (теор.) | 3,51 | 1,56 | 0,88 | 0,56 | 0,39 |
Известно, что одноименные атомы соединяются в молекулы ковалентной связью и энергии связи между валентными электронами, соответствуют дробным квантовым числам n (4). Это даёт нам возможность определить, что является источником излучения фотоэлектронов: атомы или молекулы материала фотокатода. Подставляя в формулу (5) W = 2,4 эВ и E1 = 14,05 эВ, найдем n = 2,4. Поскольку величина n оказалась дробным числом, то это значит, что источником фотоэлектронов являются не атомы, а молекулы лития (табл. 1).
Для фотоэлектрона натриевого фотокатода имеем: Ei = 5,139 эВ, E1 = 13,086 эВ и W = 2,1 эВ (1), (4). Используя математическую модель закона формирования спектров атомов и ионов (2), получим спектр фотоэлектрона натрия (табл. 2) (4).
Таблица 2
Спектр 1-го электрона атома натрия, эВ
| Значения | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 |
Eph (эксп.) | – | 3,68 | 4,31 | 4,62 | 4,78 |
Eph (теор.) | – | 3,68 | 4,32 | 4,62 | 4,77 |
Eb (теор.) | 3,27 | 1,45 | 0,82 | 0,52 | 0,36 |
Величина n, определенная с помощью формулы (5), оказывается равной n = 2,5. Из этого также следует, что источником фотоэлектронов натриевого фотокатода являются не атомы, а молекулы натрия.
Математическая модель закона формирования спектров атомов и ионов (2) показывает, что в ней нет орбитальной составляющей энергии электрона. Из этого следует, что электрон не имеет орбитального движения в атоме. Молекулы образуются путем соединения разноименных магнитных полюсов их валентных электронов, которые связаны с протонами ядер также магнитными полюсами (4), (8).
Анализ закона (2) формирования спектров атомов и ионов, и результаты расчета спектров (табл. 1 и 2) показывают, что энергия связи Eb электрона с ядром атома, а значит и энергия связи валентных электронов двух атомов друг с другом меняется ступенчато (5). Из этого следует, что кинетическая энергия фотоэлектронов Eb = Eph и величина задерживающего потенциала –V (рис. 1б) должны меняться также ступенчато. Фотоэлектроны могут поглощать лишь те фотоны, которые соответствуют энергиям их связи в молекулах данного вещества. Чем больше энергия связи между электронами в молекулах, тем большая энергия фотонов требуется для разрыва этой связи, и тем большую кинетическую энергию приобретут освобождающиеся фотоэлектроны, и тем больший потенциал потребуется для их задержания на пути к коллектору. Обратим внимание на то, что приведенная логическая цепочка явно следует из математической модели закона формирования спектров атомов и ионов (2) и неявно содержится в уравнении (1) А. Эйнштейна.
Ток в цепи существует благодаря тому, что фотоэлектроны, излученные молекулами материала фотокатода, замещаются свободными электронами. При этом они обязательно должны излучать фотоны, энергия которых равна энергии связи электронов в молекулах, но свет, падающий на фотокатод, не позволяет нам фиксировать это излучение.
Математическое уравнение А. Эйнштейна, описывающее экспериментальные закономерности фотоэффекта, имеет более глубокий физический смысл. При правильной интерпретации составляющих этого уравнения, оно становится математической моделью закона формирования спектров атомов и ионов, открытого нами в 1993 году и опубликованного в работах (4), (9), (10), (11), (12).
Шпольский Э.В. Атомная физика. – М.: Изд-во физико-математической литературы, 1963. 575 с.
Спроул Р. Современная физика. – М.: Наука, 1974. 390 с.
Вихман Э. Квантовая физика. – М.: Наука, 1977. 415 с.
Канарёв Ф.М. Начала физхимии микромира. – Краснодар, 2002. 320 с. (In Russian and in English).
Kanarev Ph.M. Modeling the Photon and Analyzing Its Electromagnetic and Physical Nature. Journal of Theoretics. Vol. 4...1.
Kanarev Ph.M. Model for the Free Electron. Galilean Electrodynamics. Volumes 13, Special Issues 1. Spring 2002. P. 15...18.
Kanarev Ph.M. Model of the Electron. «Apeiron» V. 7, №3...4, 2000. P. 184...193.
Kanarev Ph.M. Electrons in Atoms. Journal of Theoretics.
Канарёв Ф.М. Анализ фундаментальных проблем современной физики. Краснодар, 1993. 255 с.
Kanarev Ph.M. The Analytical Theory of Spectroscopy. Krasnodar, 1993. 88 p. (In English).
Kanarev Ph.M. On The Way to The Physics of The XXI Century. Krasnodar, 1995. P. 269. (In English).
Канарёв Ф.М. Закон формирования спектров атомов и ионов. Материалы международной конференции «Проблемы пространства, времени, тяготения». – С.-Пб.: Политехник, 1997. С. 30...37.