Интеграл и его применение
Реферат
Владимир 2002 год
Владимирский государственный университет, Кафедра общей и прикладной физики
Вступление
Символ интеграла введен с 1675г., а вопросами интегрального исчисления занимаются с 1696г. Хотя интеграл изучают, в основном, ученые–математики, но и физики внесли свой вклад в эту науку. Практически ни одна формула физики не обходится без дифференциального и интегрального исчислений. Поэтому, я и решила исследовать интеграл и его применение.
История интегрального исчисления
История понятия интеграла тесно связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи на вычисление площадей. Латинское слово quadratura переводится как “придание квадратной формы”. Необходимость в специальном термине объясняется тем, что в античнoe время (и позднее, вплоть до XVIII столетия) еще не были достаточно развиты представления о действительных числах. Математики оперировали с их геометрическими аналогами или скалярными величинами, которые нельзя перемножать. Поэтому и задачи на нахождение площадей приходилось формулировать, например, так: «Построить квадрат, равновеликий данному кругу». (Эта классическая задача “о квадратуре круга” круга» не может, как известно, быть решена с помощью циркуля и линейки.)
Символ ò введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summ a). Само слово интеграл придумал Я. Б е р н у л л и (1690 г.). Вероятн о, оно происходит от латинского integro , которое переводится как приводит ь в прежнее состояние, восстанавливать. (Действительно, операция интегрирования « восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина инте грал иное: слово integer означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласил ись с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики—интегральное исчисление (calculus integralis ), которое ввел И. Бернулли.
Другие известные ермины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило бол ее раннее «примитивная функция», которое ввел Лагранж (1797 г.). Латинское сл ово primitivus переводится как «начальный»: F(x) = ò f(x)dx — начальная (или первоначальная, или первообразная) для f (x), которая получается из F(x) дифференцированием.
В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что вс е первообразные функции отличаются на произвольну ю постоянну ю. b
А ò f(x)dx
a
называют определенным интегралом (обоз начение ввел К. Фурье (1768—1830), но пределы интегрирования указывал уже Эй лер).
Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т. е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 — ок. 355 до н.э.). С помощью этого метода Евдокс доказал, например, что площади двух кругов относятся как квадраты их диаметров, а объем конуса равен 1/3 объёма цилиндра, имеющего такие же основание и высоту.
Метод Евдокса был усовершенствован Архимедом. Основные этапы, характеризующие метод Архимеда: 1) доказывается, что площадь круга меньше площади любого описанного около него правильного многоугольника, но больше площади любого вписанного; 2) доказывается, что при неограниченном удвоении числа сторон разность площадей этих многоугольн иков стремится к нулю; 3) для вычисления площади круга остается найти значение, к которому стремится отношение площади правильного многоугольника при неограниченном удвоении числа его сторон.
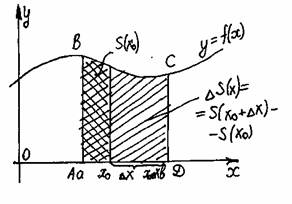
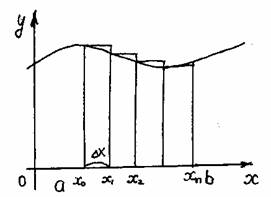
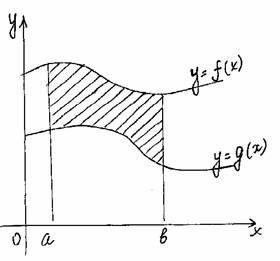
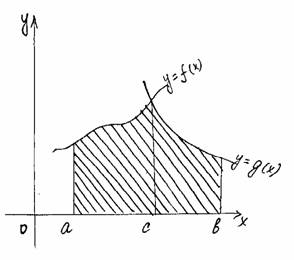
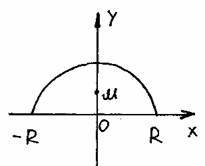
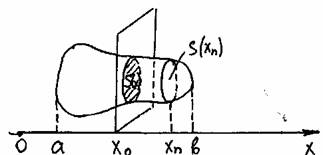
С помощью метода исчерпывания, целого ряда других остроумных соображений (в том числе с привлечением моделей механики) Архимед решил многие задачи. Он дал оценку числа p (3.10/71 Архимед предвосхитил многие идеи интегрального исчисления. (Добавим, что практически и первые теоремы о пределах были доказаны им.) Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления. Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод — метод неделимых, который также зародился в Древней Греции (он связан в первую очередь с атомистическими воззрениями Демокрита). Например, криволинейную трапецию (рис. 1, а) они представляли себе составленной из вертикал ьных отрезков длиной f(х), которым тем не менее приписывали площадь, равну ю бесконечно малой величине f(х)dx . В соответствии с таким пониманием искомая площадь считалась равной сумме S = å f(x)dx a бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме — нули, но нули особого рода, которые, сложенные в бесконечном числе, дают вполне определенную положительную сумму. На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571—1630) в своих сочинениях “Новая астрономия”. Рис 1. (1609 г.) и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры ограниченной эллипсом) и объемов (тело разрезалось на 6ecконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598—1647) и Э.Торричелли (1608—1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип, введенный им при некоторых дополнительных предположениях. Пусть требуется найти площадь фигуры, изображенной на рисунке 1,б, где кривые, ограничивающие фигуру сверху и снизу, имеют уравнения y = f(x) и y=f(x)+c. Представляя фигуру составленной из «неделимых», по терминологии Кавальери, бесконечно тонких столбиков, замечаем, что все они имеют общую длину с. Передвигая их в вертикальном направлении, можем составить из них прямоугольник с основанием b—а и высотой с. Поэтому искомая площадь равна площади полученного прямоугольника, т.е. S = S1 = c ( b – а ). Общий принцип Кавальери для площадей плоских фигур формулируется так: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины (рис. 1,в). Тогда площади фигур Ф1 и Ф2 равны. Аналогичный принцип действует в стереометрии и оказывается полезны м при нахождении объемов. В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П.Ферма уже в 1629 г. задачу квадратуры любой кривой у = хn, где п — целое (т.е по существу вывел формулу ò хndx = (1/n+1)хn+1), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу (1630—1677), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функций в виде степенных рядов. Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия исчисления еще не было. Необходимо было выделить общие идеи лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известным под названием формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научится находить первообразные многих функций, дать логические нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М.В.Остроградский (1801—1862), В.Я.Буняковский (1804—1889), П.Л.Че бышев (1821—1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции. Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О.Коши, одного из крупнейших математиков, немецкого ученого Б.Римана (1826—1866), французского математика Г.Дарбу (1842—1917). Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1838—1922) теории меры. Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875—1941) и А. Данжуа (188 4—1974), со ветским математиком А. Я. Х инчинчин ым (1894—1959). Если F(x) – одна из первообразных функции f(x) на промежутке J, то первообразная на этом промежутке имеет вид F(x)+C, где CÎR. Определение. Множество всех первообразных функции f(x) на промежутке J называется определенным интегралом от функции f(x) на этом промежутке и обозначается ò f(x)dx. ò f(x)dx = F(x)+C, где F(x) – некоторая первообразная на промежутке J. f – подынтегральная функция, f(x) – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования. Свойства неопределенного интеграла. (ò f(x)dx) ¢ = ò f(x)dx , ò f(x)dx = F(x)+C, где F ¢(x) = f(x) (ò f(x)dx) ¢= (F(x)+C) ¢= f(x) ò f ¢(x)dx = f(x)+C – из определения. ò k f (x)dx = k ò f¢(x)dx если k – постоянная и F ¢(x)=f(x), ò k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k ò f¢(x)dx ò ( f(x)+g(x)+...+h(x) )dx = ò f(x)dx + ò g(x)dx +...+ ò h(x)dx ò ( f(x)+g(x)+...+h(x) )dx = ò (F ¢(x)+G ¢(x)+...+H ¢(x))dx = = ò (F(x)+G(x)+...+H(x)) ¢dx = F(x)+G(x)+...+H(x)+C= = ò f(x)dx + ò g(x)dx +...+ ò h(x)dx, где C=C1+C2+C3+...+Cn. Табличный способ. Способ подстановки. Если подынтегральная функция не является табличным интегралом, то возможно (не всегда) применить этот способ. Для этого надо: разбить подынтегральную функцию на два множителя; обозначить один из множителей новой переменной; выразить второй множитель через новую переменную; составить интеграл, найти его значение и выполнить обратную подстановку. Примечание: за новую переменную лучше обозначить ту функцию, которая связана с оставшимся выражением. Примеры: 1. ò xÖ(3x2–1)dx; Пусть 3x2–1=t (t³0), возьмем производную от обеих частей: 6xdx = dt xdx=dt/6 3 ó dt 1 1 ó 1 1 t 2 2 1 ———Ø ô— t 2 = — ô t 2dt = – ——– + C = —Ö 3x2–1 +C õ 6 6 õ 6 3 9 2. t ò sin x cos 3x dx = ò – t3dt = – – + C 4 Пусть cos x = t -sin x dx = dt Метод преобразования подынтегральной функции в сумму или разность: Примеры : ò sin 3x cos x dx = 1/2 ò (sin 4x + sin 2x) dx = 1/8 cos 4x – ¼ cos 2x + C ó x4+3x2+1 ó 1 1 ô———— dx = ô( x2+2 – ——– ) dx = — x2 + 2x – arctg x + C õ x2+1 õ x2+1 3 Примечание: при решении этого примера хорошо делать многочлены ”углом”. По частям Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу. (u(x)v(x))’=u’(x)v(x)+u(x)v(x) u’(x)v(x)=(u(x)v(x)+u(x)v’(x) Проинтегрируем обе части ò u’(x)v(x)dx=ò (u(x)v(x))’dx – ò u(x)v’(x)dx ò u’(x)v(x)dx=u(x)v(x)dx – ò u(x)v’(x)dx Примеры: ò x cos (x) dx = ò x dsin x = x sin x – ò sin x dx = x sin x + cos x + C x = u(x) cos x = v’(x) Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией. Способы нахождения площади криволинейной трапеции Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке (a;b), то площадь соответствующей криволинейной трапеции равна приращению первообразных. Дано: f(x)– непрерывная неопр. функция, xÎ(a;b). Доказать: S = F(b) – F(a), где F(x) – первообразная f(x). Доказательство: 1) Рассмотрим вспомогательную функцию S(x). Каждому xÎ(a;b) поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой, проходящей через точку с этой абциссой и параллельно оси ординат. Следовательно S(a)=0 и S(b)=Sтр Докажем, что S(a) – первообразная f(x). D( f ) = D(S) = (a;b) S’(x0)= lim( S(x0+Dx) – S(x0) / Dx ), при Dx®0 DS – прямоугольник Dx®0 со сторонами Dx и f(x0) S’(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) – Dx®0 Dx®0 первообразная f(x). Следовательно по теореме об общем виде первообразной S(x)=F(x)+C. Т.к. S(a)=0, то S(a) = F(a)+C C = –Fa S = S(b)=F(b)+C = F(b)–F(a) II. 1). Разобьем отрезок (a;b) на n равных частей. Шаг разбиения Dx=(b–a)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx= n®¥ = lim Dx(f(x0)+f(x1)+...+f(xn)) При n®¥ получим, что Sтр= Dx(f(x0)+f(x1)+...+f(xn)) Предел этой суммы называют определенным интегралом. Sтр=ò f(x)dx a Сумма стоящая под пределом, называется интегральной суммой. Определенный интеграл это предел интегральной суммы на отрезке (a;b) при n®¥. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала. a — нижний предел интегрирования; b — верхний. Формула Ньютона–Лейбница. Сравнивая формулы площади криволинейной трапеции делаем вывод: если F – первообразная для b на (a;b), то ò f(x)dx = F(b)–F(a) a ò f(x)dx = F(x) ô = F(b) – F(a) a a Свойства определенного интеграла. 1. ò f(x)dx = ò f(z)dz a a 2. a ò f(x)dx = 0 a a ò f(x)dx = F(a) – F(a) = 0 a 3. b a ò f(x)dx = – ò f(x)dx a b b a ò f(x)dx = F(a) – F(b) ò f(x)dx = F(b) – F(a) = – (F(a) – F(b)) a b Если a, b и c любые точки промежутка I, на котором непрерывная функция f(x) имеет первообразную, то b c b ò f(x)dx = ò f(x)dx + ò f(x)dx a a c F(b) – F(a) = F(c) – F(a) + F(b) – F(c) = F(b) – F(a) (это свойство аддитивности определенного интеграла) Если l и m постоянные величины, то ò (lf(x) +m j(x))dx = l ò f(x)dx + m òj(x))dx – a a c – это свойство линейности определенного интеграла. 6. ò (f(x)+g(x)+...+h(x))dx = ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx a a a a ò (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) – a – (F(a) + G(a) +...+ H(a)) +C = = F(b)–F(a)+C1 +G(b)–G(a)+C2+...+H(b)–H(a)+Cn= = ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx a a a Набор стандартных картинок Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)³0. Надо: рассмотреть симметрию функции относительно оси OX. ABCD®A’B’CD b S(ABCD)=S(A’B’CD) = ò –f(x)dx a b b S= ò f(x)dx = ò g(x)dx a a c b S = ò (f(x)–g(x))dx+ò(g(x)–f(x))dx a c f(x)® f(x)+m g(x)®g(x)+m S= ò (f(x)+m–g(x)–m)dx = a = ò (f(x)– g(x))dx a Если на отрезке (a;b) f(x)³g(x), то площадь между этими графиками равна ò ((f(x)–g(x))dx a Функции f(x) и g(x) произвольные и неотрицательные S=ò f(x)dx – ò g(x)dx = ò (f(x)–g(x))dx a a a b b S=ò f(x)dx + ò g(x)dx a a I. В физике. Работа силы (A=FScosa, cosa ¹ 1) Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно d(mu2/2) = Fds приращение кинетической энергии частицы за время dt равно скалярному произведению Fds, где ds – перемещение частицы за время dt. Величина dA=Fds называется работой, совершаемой силой F. Пусть точка движется по оси ОХ под действием силы, проекция которой на ось ОХ есть функция f(x) (f–непрерывная функция). Под действием силы точка переместилась из точки S1(a) в S2(b). Разобьем отрезок (a;b) на n отрезков, одинаковой длины Dx = (b – a)/n. Работа силы будет равна сумме работ силы на полученных отрезках. Т.к. f(x) –непрерывна, то при малом (a;x1) работа силы на этом отрезке равна f(a)(x1–a). Аналогично на втором отрезке f(x1)(x2–x1), на n-ом отрезке — f(xn–1)(b–xn–1). Следовательно работа на (a;b) равна: А » An = f(a)Dx +f(x1)Dx+...+f(xn–1)Dx= = ((b–a)/n)(f(a)+f(x1)+...+f(xn–1)) Приблизительное равенство переходит в точное при n®¥ А = lim ((b–a)/n) ( f(a)+...+f(xn–1))= ò f(x)dx (по определению) n®¥ a Пример. Пусть пружина жесткости С и длины l сжата на половину свой длины. Определить величину потенциальной энергии Ер равна работе A, совершаемой силой –F(s) упругость пружины при её сжатии, то l/2 Eп = A= – ò (–F(s)) dx 0 Из курса механики известно, что F(s)= –Cs. Отсюда находим l/2 l/2 Еп= – ò (–Cs)ds = CS2/2 | = C/2 l2/4 0 0 Ответ: Cl2/8. Координаты центра масс Центр масс – точка через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела. Пусть материальная однородная пластина о имеет форму криволинейной трапеции {x;y |a£x£b; 0£y£f(x)} и функция y=f(x) непрерывна на (a;b), а площадь этойкриволинейной трапеции равна S, тогда координаты центра масс пластины о находят по формулам: x0 = (1/S) ò x f(x) dx; y0 = (1/2S) ò f 2(x) dx; a a Примеры. Центр масс. Найти центр масс однородного полукруга радиуса R. Изобразим полукруг в системе координат OXY. Из соображений симметрии и однородности замечаем, что абсцисса точки M xm=0 Функция, описывающая полукруг имеет вид: y = Ö(R2–x2) Пусть S = pR2/2 — площадь полукруга, тогда R R y = (1/2S) òÖ(R2–x2)dx = (1/pR2) òÖ(R2–x2)dx = –R –R R = (1/pR2)(R2x–x3/3)|= 4R/3p –R Ответ: M(0; 4R/3p ) Путь, пройденный материальной точкой Если материальная точка движется прямолинейно со скоростью u=u(t) и за время T= t2–t1 (t2>t1) прошла путь S, то t2 S=ò u(t)dt. t1 В геометрии Объём — количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1ди, 1м и т.д.). Количество кубов единичного объёма размещенных в данном теле — объём тела. Аксиомы объёма: Объём — это неотрицательная величина. Объём тела равен сумме объёмов тел, его составляющих. Найдем формулу для вычисления объёма: выберем ось ОХ по направлению расположения этого тела; определим границы расположения тела относительно ОХ; введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка (a;b) поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ. разобьем отрезок (a;b) на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx n®¥ Dx®0, а Sk®Sk+1, а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH. Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при n®¥ называется интегралом a ò S(x)dx a V= ò S(x)dx, где S(x) – сечение плоскости, проходящей через b выбранную точку перпендикулярно оси ОХ. Для нахождения объема надо: 1). Выбрать удобным способом ось ОХ. 2). Определить границы расположения этого тела относительно оси. 3). Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку. 4). Выразить через известные величины функцию, выражающую площадь данного сечения. 5). Составить интеграл. 6). Вычислив интеграл, найти объем. Объем фигур вращения Тело, полученное в результате вращения плоской фигуры, относительно какой-то оси, называют фигурой вращения. Функция S(x) у фигуры вращения есть круг. Sсеч = pr2 Sсеч(x)=p f 2(x) V= ò f 2(x) a Длина дуги плоской кривой Пусть на отрезке (a;b) функция y = f(x) имеет непрерывную производную y’ = f ’(x). В этом случае длину дуги l “куска” графика функции y = f(x), xÎ(a;b) можно найти по формуле l = ò Ö(1+f’(x)2)dx a М.Я.Виленкин, О.С.Ивашев–Мусатов, С.И.Шварцбурд, “Алгебра и математический анализ”, Москва,1993г. “Сборник задач по математическому анализу”, Москва,1996г. И.В.Савельев, “Курс общей физики”, том 1, Москва, 1982г.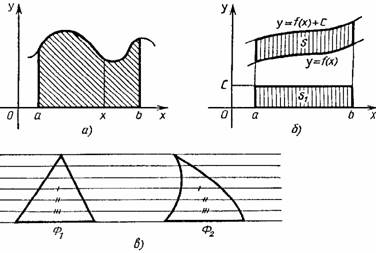
Определение и свойства интеграла
Интегрирование
Криволинейная трапеция
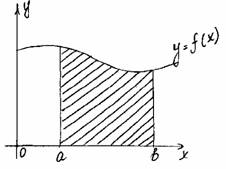
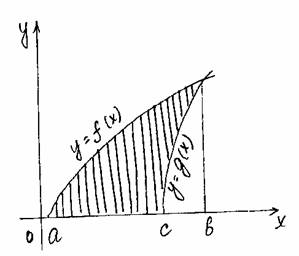
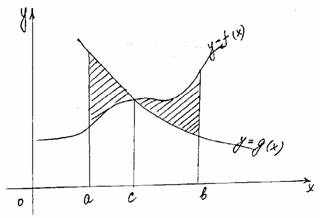
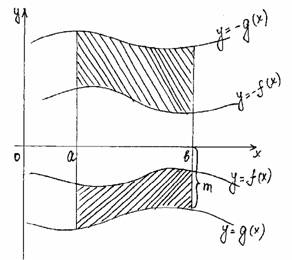
Применение интеграла
Список литературы
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Важнейшие достижения в освоении космоса
- Фундаментальная проблема астрофизики
- Движение астероидов
Все открытые до сих пор астероиды обладают прямым движением : они движутся вокруг Солнца в ту же сторону, что и большие планеты (i
- Второе начало термодинамики
ВведениеЧем глубже проникают исследователи в тайны природы, тем больше стираются границы между отдельными областями науки и тем трудне
- Жидкие кристаллы, история открытия жидких кристаллов, структура, типы и их применение
Реферат по физикеВыполнил студент I курса группы Н-5972 Глухенький Р.Е.Дальневосточный Государственный Технический УниверситетВладивост
- Производная и ее применение в алгебре, геометрии, физике
0.Периметр убывает в промежутке 0x2 f(x1)0.∆x→0 Доказательство от противного. Пусть для определенности f '(c)>0, т. е.Предположим, что при стр
- Нестандартный анализ
Курсовая работа по курсу «Математика»Кировоградский государственный педагогический университет им. ВинниченкаКировоград 2003 Вступлен
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

