referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Инженерия знаний
Система - посредник, заключение договора на поставку.
Инженерия знаний - область информатики, в рамках которой проводятся исследования по представлению знаний в ЭВМ, поддержание их в актуальном состоянии и манипулировании ими.
Knowledge system - система основанная на знаниях.
СОЗ СБЗ СУБД ЭС ИС СИИ - система искусственного интеллекта.
Структура системы, основанной на знаниях.
Б
З механизм получения решения
ИНТЕРФЕЙС
БЗ - это модель, представляющая в ЭВМ знания, накопленные в определенной предметной области. Эти знания должны быть формализованы. Знания формируются с помощью модели, а затем представляются с помощью определенного языка.
В БЗ обычно выделяются знания о конкретных объектах и правила. Эти правила исполняются как механизм получения решений, для того, чтобы из исходных фактов вывести новые.
Интерфейс обеспечивает ведение диалога на языке, близком пользователю.
Методы, основанные на использовании логических выводов, часто используется в инженерии знаний.
Понятие предметной области.
Объект – то что существует или воспринимается в качестве отдельной сущности.
Основные свойства: дискретность; различие.
При представлении знаний используется прагматический подход, т.е. выделяются те свойства объекта, которые важны для решения задач, которые будет решать создаваемая система. Поэтому система, основанная на знаниях, имеет дело с предметами, которые являются абстрактными объектами. Предмет выступает в роли носителя некоторых свойств объекта. Состояние предметной области может меняться со временем. В каждый момент времени состояние предметной области характеризуется множеством объектов и связями. Состояние предметной области характеризуется ситуацией.
Ситуация
Статическая
Динамическая
Постоянные свойства и соотношения
Состояния
Устойчивые
Временные
Процессы
События
Концептуальные средства описания предметной области.
Концептуальная модель отражает наиболее общие свойства. Для того, чтобы детализировать описание нужны языки. Характерными чертами концептуальных средств описания предметной области являются абстрактность и универсальность. Их можно использовать для описания любой предметной области.
Понятие класса объекта.
Понятие объекта – понятие множеств. Сходные между собой объекты объединяются в классы. В разные моменты времени одному и тому же классу могут соответствовать разные множества объектов.
К – класс объекта.
Кt – множество объектов класса К в момент времени t.
К = t Кt
Пример:
Группа (1999) = { ИА-1-99, ИА-1-98, … , ИА-1-94, ИБ-1-99,…}
Группа (1998) = { ИА-1-98, ИА-1-97, … , ИА-1-93, ИБ-1-98,…}
t Кt = { … }
Преподавательская должность = { профессор, доцент, старший преподаватель, преподаватель, ассистент}
зел
син
1
син
желт
4 Геометрическая фигура, форма квадрат, цвет синий.
2
зел
5
3
(К : А1 К1, А2К2, … , АnКn)
имя атрибут название
классов классов
о
бъектов атрибутная пара
Идентификация объектов может быть прямая и косвенная. В случае прямой используются имена объектов, порядковые номера объектов; косвенная основана на использовании свойств объектов.
Атрибут может быть компонентом. Под атрибутом понимается свойство, характеристика, название компонентов.
Пример:
(Геометрическая фигура:
форма Геометрическая форма
цвет Цвет)
Пары имя атрибута и значение атрибута часто совпадают.
Пример ситуации:
(Лекция:
лектор Фамилия_лектора,
место №_аудитории,
тема Название_темы,
слушатель Код_группы,
день День_недели,
время Время_начала)
Ситуация – показана связь между «преподаватель» и «слушатель», остальные характеристики данной ситуации.
Роли участников ситуации:
лектор
место
слушатель
Характеристики ситуации:
день
время
(К: А1К1,А2К2, … , АnКn) – представление знаний в виде некоторой структуры.
(К: АiКi)
Пример:
(дата, число, день_месяца)
(дата, месяц, название_месяца)
(дата, год, год)
(геометрическая_фигура, форма, геометрическая_форма)
(геометрическая_фигура, цвет, цвет)
Такому представлению знаний соответствует представление знаний в виде отдельных фактов.
(К: АiКi)
(К: А1К1,А2К2, … , АnКn)
Представления знаний об объектах делятся на:
классы объекта (структура данных)
знания о конкретных объектах (о данных)
Классы объекта.
(К: А1К1,А2К2, … , АnКn)
Аi – имя атрибута
Кi – классы объекта, являются значением атрибута
К – имя класса
Пример:
(преподаватели:
ФИО фамилия_с_инициалами,
Должность преподпвательская_должность)
(К: АiКi)
Пример:
(преподаватель, ФИО фамилия_с_инициалами,
преподаватель, должность преподпвательская_должность)
К (К1,К2, … , Кn)
К (А1,А2, … , Аn)
Пример:
(преподаватель (фамилия_с_инициалами, преподпвательская_должность),
преподаватель (ФИО, должность))
Представление знаний для первой формы:
(К: А1К1,А2К2, … , АnКn) кi Кi
Атрибутивное представление знаний:
Пример:
(преподаватель: - представляет собой
ФИО Семенов - некоторую структуру
Должность доцент) - данных
Представление знаний для второй формы:
(К: АiКi) к К, кi Кi
Атрибутивное представление знаний в виде отдельных фактов:
Пример:
(преподаватель1, ФИО, Семенов) - 1, 2 являются связками между
(преподаватель1, должность, доцент) - фактами
(преподаватель2, ФИО, Петров)
(преподаватель2, должность, ассистент)
Представление знаний для третьей формы:
К (К1,К2, … , Кn)
(преподаватель (Семенов, доцент) - позиционное представление знаний
Если имена атрибутов отсутствуют, а сами атрибуты записываются на определённых позициях, то – позиционноё представление знаний.
Представление знаний в виде «троек» - (объект, атрибут, значение).
Для представления неточных значений используются коэффициенты уверенности – (объект, атрибут, значение, коэффициент уверенности).
Пример:
(пациент1, диагноз, колит, К760)
0 100
0 1
-1 1
0 – соответствует неопределенности.
отрицательное значение – степень уверенности в невозможности значения атрибута.
(
(пациент1, диагноз, колит, К760)
(пациент1, диагноз, гастрит, К740)
*
пациент1, диагноз, гастрит, К740)
* (пациент, ФИО, Антонов, диагноз колит К760, гастрит К740)
Представление знаний о классе объекта называется минимальным, если при удалении одного из атрибутов приводит к тому, что оставшееся множество атрибутов перестает быть представлением данного класса объекта.
Пример:
Аренда (объект_аренды, арендатор, арендодатель, срок_аренды, плата).
Если удалить «срок_аренды», получится купля-продажа, а если удалить «срок_аренды» и «плата», то получиться подарок.
Представление знаний в реляционной базе данных.
Реляционная база данных – данные хранятся в позиционном формате.
Данные хранятся в виде таблицы, где название таблицы – имя класса. Каждому классу соответствует таблица или файл БД. Имя класса - название соответствующей таблицы. Имена атрибутов – соответствующие поля таблицы (столбец). Строки таблицы – записи БД. Записи соответствует запись в позиционном формате.
А1
А2
. . . . . Аn
К1
К2
. . . . . Кn
Преподаватели
ФИО
должность Семенов
Петров
Доцент
ассистент
Понятие атрибута в позиционной БД сохраняется.
Запись К (А1,А2, … , Аn) называется отношение между атрибутами. Такая терминология используется в реляционной БД. Идея данных в реляционной БД основана на понятие «ключ».
Ключ – набор атрибутов отношения, значение которых однозначно определяет запись в файле.
Квартира
| город | улица | дом | корпус | квартира | площадь | количество комнат |
Москва Москва | Тверская Тверская | 2 2 | 1 1 | 47 54 | 60 50 | 2 1 |
В данном случае ключ будет состоять из нескольких полей.
К
i sup Кj является подклассом класс sup подкласс; подкласс sup класс.
Кi является подклассом Кj, если t Kit Kjt
(Если в любой момент времени t класс Кi является подклассом Кj)
Npr – классификация сети.
Классификация сети представляется в виде иерархической структуры.
С
sup
sup
sup
sup
sup
учащийся
тудент sup учащийся.
K
sup
sup
sup
sup
sup
sup
sup
sup
sup
sup
sup
sup
sup
sup
студент
объект
Неопределенный объект
Определенный объект
Материальный объект
Нематериальный объект
имя
понятие
ситуация
время
пространство
человек
помещение
оборудование
учащиеся
административный персонал
преподаватели
обслуживающий персонал
студент
аспирант
декан
заведующий кафедрой
методист
профессор
ассистент
доцент
техник
лаборант
i part of Kj - является частью Ki part Kj
Ki является частью Kj, если конкретный объект класса Ki является частью однозначно определенного объекта Kj.
part
part
sup
sup
время
part
part
part
part
год
неделя
месяц
сутки
час
минута
секунда
part
part
part
пространство
sup
sup
sup
sup
страна
область
губерния
штат
населенный пункт
город
деревня
Отношение принадлежности.
k
isa
город
Москва
isa K - является элементом
K
i ius K - является составляющей
К1 ius K
K2 ius K
. . . . . . .
Kn ius K
Означает, что объект класса К состоит из объектов класса К1, К2, … , Кn, причем объект класса К может включать несколько объектов класса Кi.
Лекция №4.
Свойства отношений.
Отношения частичного порядка обладают свойством транзитивности.
Ki sup Kj Kj sup Km
Ki sup Km
Ki part Kj Kj part Km
Ki part Km
Если элемент является составляющей блока, а блок составлен…
Нет циклов в графе принадлежности.
K1 ins K2, K2 ins K3,…,Kn-1 ins Kj
Неверно, что Kn ins K1
K isa Ki sup Kj
K isa Kj
Москва isa город
Город sup Населенный пункт
Москва isa Населенный пункт
K1
K2
K3
K5
K4
R6
R7
R3
R2
R1
R5
R4
Операции над классами объектов.
С помощью операций над классами объектов можно определить новый класс объектов
Ki ins K
℧ Ki множество блоков, к примеру, телевизоров
Ki sup K
℧ Ki = K
Материальные объекты делятся на три класса
Условие Помещение Оборудование = Материальный объект
Человек Помещение = Человек Оборудование = Помещение Оборудование =∅
Размещение классов объекта
Человек (Фамилия, Имя, Отчество, Год_Рождения, пол)
Пол={мужской, женский}
Мужчина, женщина = Человек\пол
K (K1, K2, K3, K4, K5)
K\K5 – Разбиение класса по классу К5.
Объединение всех этих классов есть человек.
Мужчина⋃Женщина=Человек
Мужчина⋃Женщина=∅
(Знание_иностранного языка
Знающий человек,
Предмет иностранный_язык)
(K A1K1, A2K2)
K1/(K, K2)
В результате разбиения мы получаем классы людей, знающих иностранный язык.
Концептуальной схемой предметной области называется множество классов объектов, заданных на нем отношений и операциями.
Шаблонные описания состояния предметной области:
Занятия K
<Преподаватель> проводит занятия по дисциплине <название дисциплины> в группе <код группы> в <день недели> на <номер пары> в <аудитории>.
Иванов И.И. проводит занятия по дисциплине ТОЭ в группе ИТ-1-98 в понедельник на 4 паре в Г-301.
(занятия:
преподаватель Преподаватель
дисциплина Название_дисциплины
группа Код_группы
день День_недели
время Номер_пары
место Аудитория)
Концептуальные модели предметной области – концептуальная схема вместе с множеством высказываний построенных по конечному набору шаблонов.
Диаграмма сущности и связи (ER – диаграмма)
Entety Relation Diagramm
С
ущность
связь
Атрибуты сущности и связи
преподаватель
кафедра
N 1
*
На 1 кафедре работает N преподавателей. «*» – знак преподавателя – можно найти кафедру.
Связь глагол или дополнение
дисциплина
Группа
Атрибуты – прилагательное, числители, размеры, место действия
факультет
Код специальности
специальность
Назв. Спец.
Расписание нагрузки
Зав. кафедрой
преподаватель
группа
дисциплина
Логические системы (модели), на основе единственного примера поставки товара в магазин.
Логические модели представления знаний.
Описание предметной области на одном из логических языков программирования, основано на исчислении предикат.
Язык многократного исчисления предикатов 1-го порядка. Многократная логика 1-го порядка.
Для составления этого языка :
Понятие сорта соответствует понятию классов объектов.
Множество сортов S
- на множестве задаются функциями.
f-имя функции;
сорта аргументов;
В – сорт значения функции.
Z – сигнатура – это верхний уровень представления знаний в логических моделях.
Предикат - 
Т
={0;1}
ложь истина
-константа сорта В
Рассмотрим в качестве примеров обработку деталей на производстве
2-токарных;
1-фрезерный;
S={Деталь, Станок, Операция, Тип_детали, Тип_станка, Время }
1) дет: Операция Деталь;
f A1 B
2) ст: Операция Станок;
3) нач: Операция Время
4) кон: Операция Время
5) тип_дет: Деталь Тип_детали
6) тип_ст: Станок Тип_станка
7) 0 : Время
C B
1: Время
. В
.
.
t: Время
8) ст_вал:Тип_детали
вал_мест: Тип_детали
9) фрез: Тип_станка
ток: Тип_станка
10) фрез_торц:операция Т
ток_обр: операция Т
11) +: Время*Время Время
12)
: Время*Время Т
Знания о конкретных объектах
(нижн. Уровень представления знаний) на языке многократного исчисления предикатов наз-ся структурой интегрированной сигнатурой
сигнатура
Структура интегр. Сигнатуры.
Для каждого имя сорта создаётся мн-во объектов этого сорта.
Деталь = {дет.1, дет.2, дет.3, дет.4}
Станок = {ст.1, ст.2, ст3}
Операция ={опер1,опер2, опер3, опер4, опер5, опер6, опер7, опер8}
Тип_детали = {ст_вал, вал_мест}
Тип_станка = {ток, фрез}
Время = {1,2,…,t}
Объединение всех множеств - универсум.
Каждой функции и предикатов из структуры в системе соответствует множество факторов.
дет.(опер.1)=дет1
дет.(опер.2)=дет1
дет.(опер.3)=дет2
…………………..
2) ст.(опер.1)= ст.3
ст.(опер.2)= ст.1
ст.(опер.3)= ст.3
…………………
3) нач.(опер.1)=0
нач.(опер.2)=5
нач.(опер.3)=5
…………………..
4) конц(опер.1)=5
конц(опер.2)=12
конц(опер.3)=0
…………………
5) тип_дет(дет.1)=ст_вал
тип_дет(дет.2)=вал_мест
тип_дет(дет.3)=ст_вал
тип_дет(дет.4)=вал_мест
………………….
6) тип_ст. (ст.1)=ток
тип_ст. (ст.2)=ток
тип_ст. (ст.3)=фрез
………………….
10) фрез_торц(опер1)
ток_обр (опер2)
фрез_торц(опер3)
| операция | деталь | станок | начало | конец | фрез_торц | ток_обр |
| Опер1 | Дет.1 | Ст.3 | 0 | 5 | 1 | 0 |
| Опер2 | Дет.1 | Ст.1 | 5 | 12 | 0 | 1 |
| Опер3 | Дет.2 | Ст.3 | 5 | 10 | 1 | 0 |
| Опер4 | Дет.2 | Ст.2 | 10 | 17 | 0 | 1 |
| Опер5 | Дет.3 | Ст.3 | 10 | 16 | 1 | 0 |
| Опер6 | Дет.3 | Ст.1 | 16 | 26 | 0 | 1 |
| Опер7 | Дет.4 | Ст.3 | 16 | 22 | 1 | 0 |
| Опер8 | Дет.4 | Ст.2 | 22 | 32 | 0 | 1 |
| Деталь | Тип_дет |
| Дет.1 | Ст_вал |
| Дет.2 | Ст_вал |
| Дет.3 | Вал_мест |
| Дет.4 | Вал_мест |
| Станок | Тип_ст |
| Ст.1 | Ток. |
| Ст.2 | Ток. |
| Ст.3 | Фрез. |
3) Составляющая : Логические формулы
Правила построения формул:
а)константа сорта А, есть терм сорта А
б)переменная принимающая значение из сорта А, есть терм сорта А
в)если сигнатура содержит функцию
-
построенные термы сортов 
соответственно, то
-есть терм сорта В
г)если сигнатура содержит предикат-
,термы построенных сортов
, то 
- есть атом.
д)если 
- термы одинакового сорта, то выражение 
, то есть атом
е)Атом есть формула правильно построенная (ППФ)Переменная, входящая в атом, является свободной в этом атоме.
ж)если 
построенная формула в которую свободно входит переменные х сорта А , то выражения:
также является ППФ, переменная “x” является
связанной (в новых файлах)
з)если 
уже построенные формулы, то 
, также
является ППФ
Примеры:
Представление Знания b=> опер2 выполнены на токарном станке
тип_ст(ст(опер2))=nток
Опер2 выполн на ост.1 на ст.1 нач 5 конец 12
)
3)
Лекция 8 12.11.99.
Метод резолюций
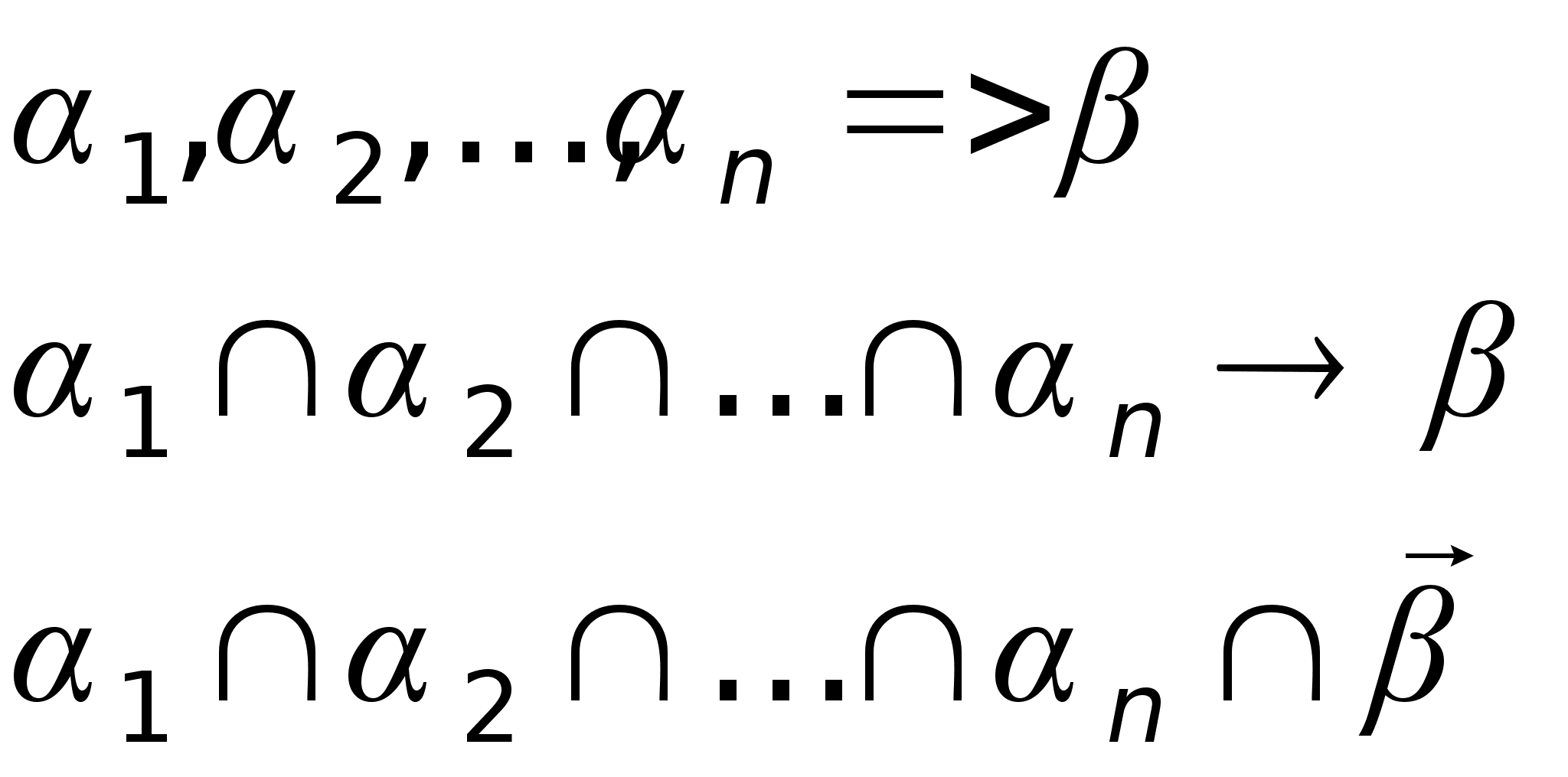
Метод резолюций доказывает невыполнимость.
Для использования этого метода необходимо исходную формулу привести к ДНФ.
ДНФ: 
- дизъюнкция литер
рii – атом или отрицание атома.
Потом ДНФ представляют в виде множества дизъюнктов
В методе резолюций – имеется одно правило вывода
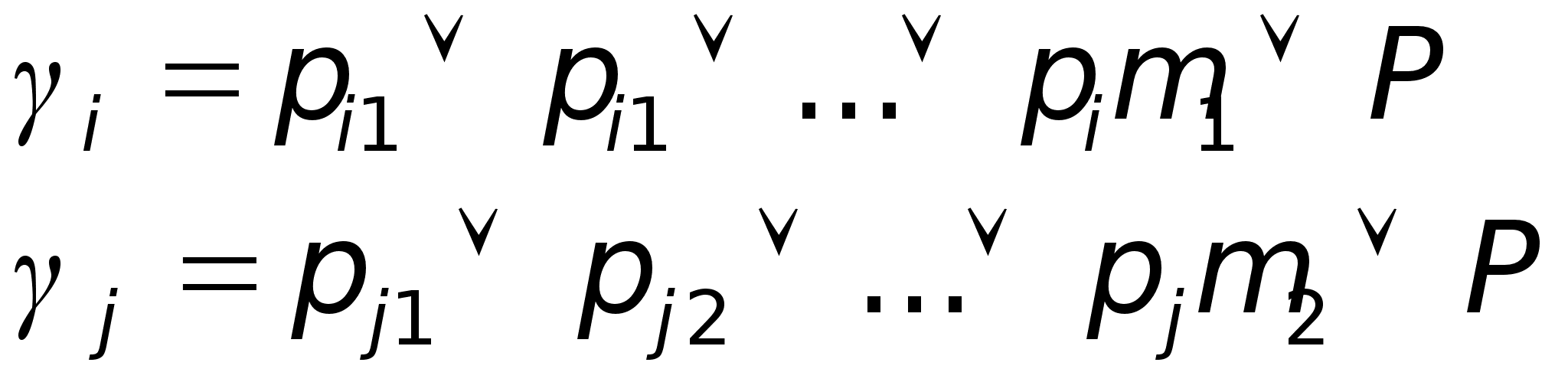
В результате из 2-х дизъюнктов получаем новую, называется руовентой
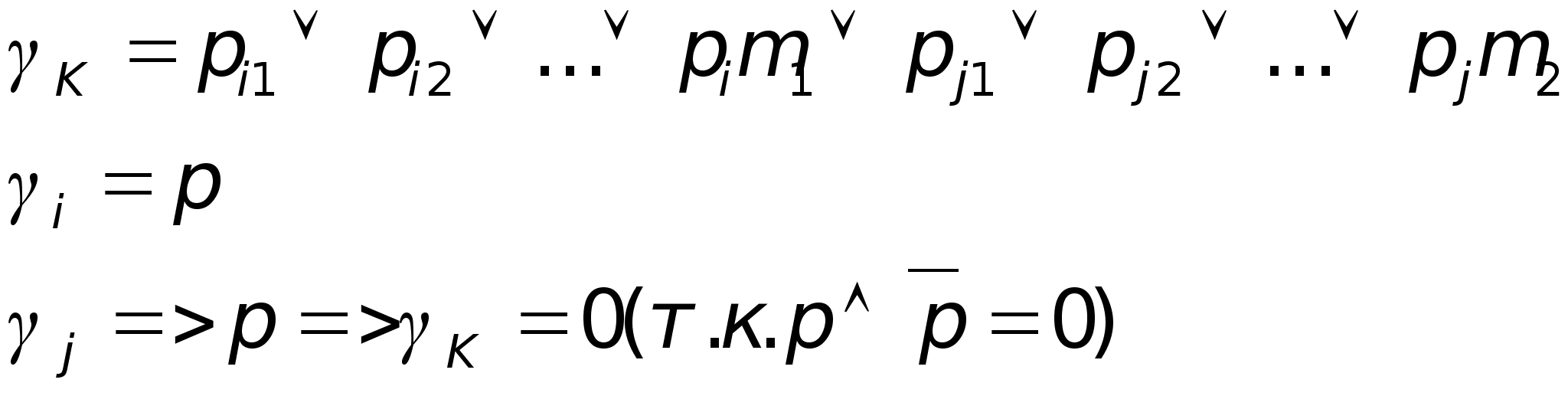
- получаем пустой дизъюнкт , который всегда ложный.
Если множество содержит пустой дизъюнкт , то оно является не выполнимым.
Получается пустой дизъюнкт, который доказывает что данное множество является невыполнимым.
Метод резолюций применяется до тех пор пока не получится пустой– дизъюнкт
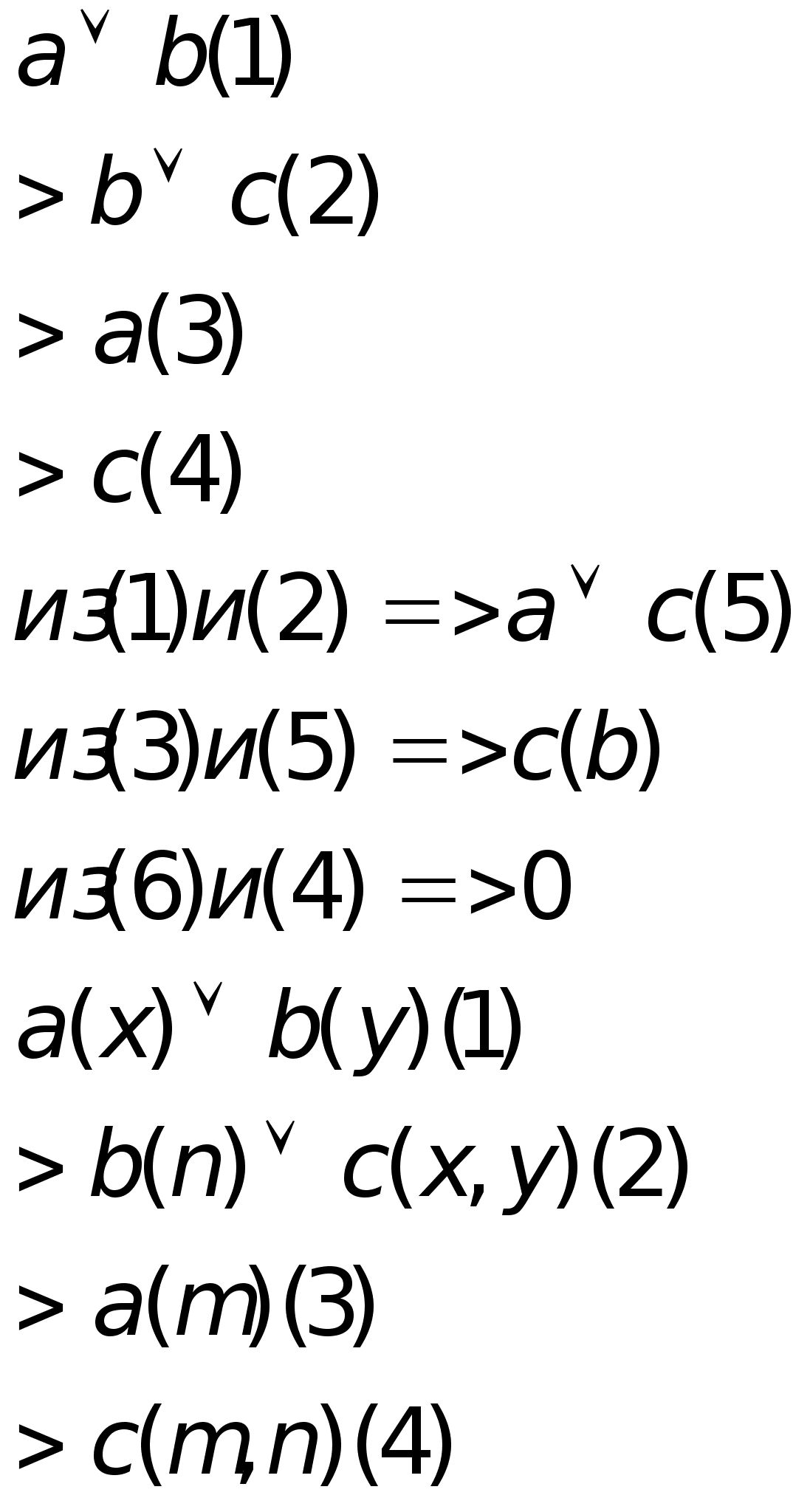
m,n – const
подстановка вместо переменной константы –унификация.
В данном случае выполняем подстановку {n/y}:
Из (1)и (2) => a(x)
c(x,n) (5)
Из (3) и (5) , выполняя ь подстановку {m/n}=> c(m,n) (6)
Из (4) и (6) без подстановок => 0
Принцип резолюций в Прологе
В Прологе используются хордовские дизъюнкты, т.е. дизъюнкты, содержащие одну литеру без отрицания.
На пример 
=>
конъюнкция
без
отрицания
Могут использоваться дизъюнкты , которые вообще не содержат литер. –
это целевое утверждение на прологе: ? – a
a: - b,c,d.
b: - e,f.
c.
e.
f.
?-a
a(1)
a(2)
a(3)
| № шага | Целевой дизъюнкт | Исходный дизъюнкт | резольвета |
1 2 3 4 5 6 | ?- a. ?-b,c,d ?-e,f,c,d ?-f,c,d ?-c,d ?-d | a:-b,c,d. b:-e,f e f c d | -b,c,d. -e,f,c,d -f,c,d -c,d -d 0 |
Представление программы в виде графа
a
: - b;c
b: - d,e
c
: - g,f.
e
: - i,h
g
: - h,j
d
.
f.
h
.
?-a
«,» - и
«;» - или
Построение графа начинается с целевого дизъюнкта.
На графе видно какие и сколько решений имеет рассматриваемая задача.
- Два решения
задачи
Продукционная модель представления знаний.
Основа для данной модели – это продукционные правила, которые имеют следующий вид
продукционное правило >:=<имя правила>
Eсли <посылка> то < заключение> (КД=<коэффициент доверия>)
Примеры:
Правило 5
Если пол=женский
И сложение=мелкое
И вес=65 лет_или_больше
То относительный_вес=изменчивый
Коэффициент доверия определяется числом 0-100
Правило 27
ЕСЛИ перспектива=отличная
И риск=высокий
ТО фактор=0 КД=10
В общем случае посылка может быть логическим выражением.
Если посылка истинна, то истинно и заключение, т.е. в заключение может быть указано какое-либо действие , которое выполняется, если посылка истинна
<посылка>::<условие>(И<условие>И…И<условие>)
<условие>::=<объект>=<значение>
объект, атрибут, значение, коэфициент доверия- представление знаний в виде четвёрки
<заключение>::=<объект>=<заключение>
<факт>:=<объект>=<значение>КД=<коэффициент доверия>
Один и тот же объект может иметь разные значения.
Многозначные объекты – объекты, которые могут иметь несколько достоверных значений.
Если объект не объявлен, как многозначный, то он может иметь несколько значений, то они не должны быть достоверными, т.е. КД= 100
Список значений
Список разрешённых
значений
объект
вопрос
Для объектов, значение которое запрашивается у пользователя.
Какое сложение?
М
елкоеСреднее разрешённые значения
Крупное
Каков возраст
меньше 25
от 25 до 55
больше 55
Коэффициент доверия посылки=min(Кдусл)
- факта, полученного в результате выполнения правила
перспектива=отличная КД=50
риск=высокий КД=70
фактор=0
Базовая структура продукционной модели представления знаний
Рабочая память(база данных)
Исходные данные
Интерпритатор правил
База правил
Результат Лекция 9 (Конец)
№ шага | Конфликтное Множество правил | Выполнение правила | Выведенный факт |
1 2 3 4 5 |
|
|
|
Выводы заканчиваются , когда достигается целевая вершина, либо не осталось применимых правил, а цель не достигнута.
Обратные выводы – выполняются сверху вниз (выводами ориентирующих на цель)
П6 П7
С2 С3
