Законы сохранения механики
Содержание
Лабораторная работа №1. Лабораторная установка «Модель копра»
Лабораторная работа №2. Определение скорости пули методом физического маятника
Лабораторная работа №3. Лабораторная установка «Маховик»
Лабораторная работа №4. Лабораторная установка «Наклонная плоскость»
Лабораторная работа №5. Определение объёма и плотности тела, вычисление погрешностей
Лабораторная работа №6. Определение момента инерции и проверка теоремы Штейнера методом крутильных колебаний
Лабораторная работа №7. Определение модуля сдвига при помощи крутильных колебаний
Лабораторная работа №8. Исследование прямолинейного движения тел в поле тяжести на машине Атвуда
модель копра теорема штейнера
Лабораторная работа №1
ЛАБОРАТОРНАЯ УСТАНОВКА «МОДЕЛЬ КОПРА»
Цель работы: Лабораторная установка «Модель копра» позволяет иллюстрировать применимость законов сохранения в механике: закона сохранения импульса, закона сохранения полной механической энергии, а также закона изменения полной механической энергии.
При работе на данной установке определяется сила сопротивления грунта при забивке сваи, оценивается доля энергии, затраченной на деформацию при неупругом ударе, а также замкнутость системы копр – свая.
Принадлежности: установка «Модель копра», габаритные размеры:
длина – не более 420 мм
ширина – 100±5 мм
высота – не более 650 мм
масса – не более 8 кг
масса гири – (435±1) г
масса груза m1 – (319±1) г
масса сваи m2 – (121±1) г
Состав изделия и комплект поставки:
– основание установки в сборе с разрезной втулкой и сваей – 1 шт.
– направляющая в сборе с защелкой и грузом – 1 шт.
– рычаг – 1 шт.
– гиря – 1 шт.
Устройство и принцип работы
Модель копра (рис. 1) состоит из груза 1, который может перемещаться по вертикальной направляющей, и сваи 2, которая с большим трением скользит в разрезной втулке 3. Сила трения между сваей и втулкой создается за счет силы нормального давления на одну из половин втулки со стороны малого плеча рычага 4. По рычагу 4 скользит гиря 5, передвигая которую можно изменять силу нормального давления.
Для удержания груза 1 на некоторой высоте служит защелка 7, которую можно перемещать по направляющей и закреплять в нужном положении стопорными винтами. Для закрепления груза последний поднимается с небольшим усилием до соприкосновения с защелкой. Освобождение груза производится нажатием на ручку 8 защелки.
Высота груза и сваи до и после удара измеряется по вертикальной линейке с помощью указателей, прикрепленных к грузу и свае.
При определении силы сопротивления грунта можно четко разграничивать три этапа движения груза и сваи:
1) почти свободное падение груза (трением между грузом и направляющей можно пренебречь);
2) неупругое взаимодействие (неупругий удар) между сваей и грузом;
3) совместное движение сваи и груза после удара до полной остановки.
Рассмотрим последовательно все этапы движения. При падении груза с высоты Н потенциальная энергия, обусловленная взаимодействием груза с Землей, переходит в кинетическую энергию движения груза. Здесь имеет место закон сохранения полной механической энергии, так как в системе груз – Земля внутренняя сила консервативна, а работа внешних сил равна нулю, т. е. имеет место равенство DW=DWk+DWn= 0.
На данном этапе изменение кинетической энергии груза
DW=m1v12/2,
где m1 – масса груза, v1 – скорость груза непосредственно перед ударом о сваю.
Изменение потенциальной энергии груза определяется тем, что он опустился с высоты Н, на которую был поднят над сваей, – m1gH. Следовательно, изменение полной механической энергии
DW= m1v12/2 – m1gH=0.
Отсюда можно найти скорость груза v1 непосредственно перед ударом о сваю:
V1 = (2gH)1/2. (1)
При дальнейшем движении груза происходит неупругое соударение со сваей, т. е. такое, при котором после удара соударяющиеся тела движутся с некоторой общей скоростью, целиком сохраняя возникшую при ударе взаимную деформацию.
При ударе груза о сваю можно применить закон сохранения импульса, так как систему можно считать приближенно замкнутой. Действительно, на систему груз – свая действуют как внешние силы (силы тяжести груза и сваи и сила сопротивления грунта), так и внутренние силы, развивающиеся между телами при соударении. Строго говоря, данная система не является замкнутой, но при условии, что внешние силы много меньше внутренних, систему можно считать приближенно замкнутой и, следовательно, применить закон сохранения импульса:
m1v1=(m1+m2)v2 , (2)
где m2 – масса сваи, v2 – общая скорость сваи и груза после удара.
Из (1) и (2) следует, что:
v2=m1v1/(mi+m2)=m1(2gH)1/2/(m1+m2) (3)
После неупругого удара груз и свая начинают двигаться замедленно до полной остановки. На этом этапе движения сила сопротивления фунта, являющаяся диссипативной, совершает работу, поэтому полная механическая энергия системы груз – свая – Земля не сохраняется:
DW=DWK +DWп=Адис, (4)
то есть изменение полной механической энергии системы равно работе сил сопротивления грунта. Если сравнить два состояния системы, первое из которых соответствует началу совместного движения груз – свая после их соударения, а второе – окончанию движения, то изменение кинетической энергии системы можно записать так:
DWK=WK2 – WK1= -(m1+m2)v22/2. (5)
Изменение потенциальной энергии будет равно:
DWП=WП2 – WП1= -(m1+m2)gS, (6)
где S – перемещение груза и сваи от начала совместного движения до полной остановки.
На участке S сила сопротивления грунта f совершает работу Адис=fS=fScosa, где a – угол между направлением силы и перемещением. Угол a=, так как сила и перемещение взаимно противоположны. Следовательно, работа силы будет отрицательной:
Адис= – fS. (7)
Под величиной силы f подразумевается среднее значение силы сопротивления, то есть f=fcp. Подставляя (5), (6), (7) в уравнение (4), получим:
–(m1+m2)v22/2 – (m1+m2)gS = – fS. (8)
Если в уравнение (8) подставить значение скорости, найденное по формуле (3), можно записать:
m12gH/(m1+m2) + (m1+m2)gS = fS.
Разделив обе части на S, получим окончательно:
f=((m12H/(S(m1+m2)) + m1+m2)g. (9)
При неупругом ударе часть механической энергии расходуется на деформацию тел, превращаясь в конечном итоге в тепловую энергию. Потерю механической энергии можно подсчитать как разность механических энергий системы после и до удара:
DW = (m1 +m2)v22/2 – m1v12/2.
Подставив из (3) значение скорости v2 и из (1) скорость v1, имеем:
DW = m12gH/(m1+m2)-m1gH = m1gH(m1/(m1+m2)-1) = m1m2gH/(m1+m2).
Удобнее не определять абсолютную величину потерь механической энергии, а рассчитывать долю механической энергии, затраченную на деформацию тел при неупругом соударении:
DW/WK2 = m1gHm2/ m1gH(m1 + m2)= m2/(m1+ m2). (10)
Анализ этого выражения позволяет сделать вывод: при забивке сваи масса груза m1 должна быть значительно больше массы сваи m2. Только в этом случае большая доля первоначальной энергии пойдет на забивку сваи.
Подготовка изделия к работе
1. Установить и закрепить на основании направляющую с защелкой и грузом.
2. Закрепить рычаг в основании.
3. Установить на рычаг гирю.
4. Собранную установку поместить на горизонтальную поверхность.
Порядок выполнения работы
1. Установить гирю 5 (см. рис. 1) на некотором расстоянии от оси вращения рычага 4.
2. Поднять сваю до предела и подобрать наибольшую высоту Н – такую, чтобы после удара свая не касалась втулки 3.
3. Подобрав нужную высоту, записать положение указателя сваи до удара S1 (рис. 1).
4. Поднять груз на выбранную высоту и закрепить его там. Записать положение указателя груза H1.
5. Нажать кнопку 8 защелки. Записать положение указателя сваи после удара S2.
6. Повторить опыт при тех же значениях H1 и S1 пять раз.
7. Следующую серию измерений проделать при том же начальном положении сваи и гири, но изменить высоту падения груза H1 при условии выполнения пункта 2. Повторить опыт пять раз. Результаты записать в табл.
8. Переставить гирю 5 на большее расстояние от оси вращения рычага. Провести третью серию измерений при тех же значениях H1 и S1, что и в пункте 7. Опыт повторить 5 раз.
Результаты измерений: S1=…..., DS1=.…..
| Серия | № опыта | H1 | S1 | H=H1-S1 | S2 | S2cp | S=S1-S2 | f |
| 1 | 1 . . 5 | |||||||
| 2 | 1 . . 5 | |||||||
| 3 | 1 . . 5 |
Для данной серии (по указанию преподавателя) записать погрешность
DН=(D Н12 + DS12)1/2, DS =(DS12+ DS22)1/2.
Обработка результатов опытов
1. По формуле (9) рассчитать среднюю силу сопротивления для каждой серии опытов.
2. Для указанной серии измерений определить погрешность силы. Пренебрегая погрешностью ускорения свободного падения и учитывая, что m1= m2, получим:
(Df)2 =2g2m2+(m12gH/S(m1+m2))2
´ (4(Dm/m1)2+2m2/(m1+m2)2+(DH/H)2+(DS/S)2)1/2.
В полученной формуле можно пренебречь первым слагаемым по сравнению со вторым. Окончательная формула для расчета погрешности имеет вид:
(Df)2=(m12gH(DS/S(m1+m2))2(4(Dm/m1)2+2Dm/(m1+m2)2+(DH/H)2 +DS/S)2). (11)
3. Записать окончательный результат в виде
f= fcp±f.
4. Определить долю энергии, затраченной на деформацию тел – формула (10).
5. Рассчитать внутренние силы, действующие в системе груз – свая во время неупругого взаимодействия тел. Для этого, используя для груза m1 соотношение D (mv) = FDt, можно записать, что
m1(v2 – v1))/ Dt = m1g + F1,
где v1 – скорость груза перед ударом, v2 – скорость груза и сваи после удара, Dt – время соударения, которое равно 2×10–4 с. Подставив значения скоростей из (1) и (3), получим формулу для расчета внутренней силы:
F = m1g + m1(2gH)1/2(1 – m1/(m1 + m2))/ Dt.
6. Сравнить внутренние силы с внешними.
Техническое обслуживание
Периодически осматривать установку и при необходимости подтягивать ослабленные винты.
Контрольные вопросы
1.Что называется импульсом тела?
2.Какая система называется замкнутой, или изолированной?
3.Сформулируйте закон сохранения импульса и закон сохранения энергии.
4.Какие виды энергии вам известны? Дайте определения механической, кинетической, потенциальной и внутренней энергиям.
5.Что называется упругим и неупругим ударами?
6.Запишите законы сохранения энергии и импульса для данной установки при упругом и неупругом ударе.
7.Выведите рабочую формулу.
Лабораторная работа №2
ОПРЕДЕЛЕНИЕ СКОРОСТИ ПУЛИ МЕТОДОМ ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы: лабораторная установка «Определение скорости пули методом физического маятника» позволяет иллюстрировать законы сохранения в механике: закон сохранения момента импульса, закон сохранения полной механической энергии и изменение полной механической энергии при неупругом ударе.
При работе на данной установке определяется скорость пули пружинного ружья по отклонению физического маятника от положения равновесия.
Приборы и принадлежности: лабораторная установка физический маятник; габаритные размеры:
длина – не более 470 мм
ширина – не более 210 мм
высота – не более 670 мм
масса – не более 7 кг
масса пули m1 = (2,4 ±0,03) г
масса стержня m2= (77 ±0,1) г
масса ловушки m3 = (12,5 ±0,5) г
расстояние от оси до центра ловушки l1 = (575 ±0,5) мм
длинна стержня l2 = (570 ± 0,5) мм
расстояние от оси до линейки l= (625 ± 0,7) мм
Состав изделия и комплект поставки:
– основание с закрепленными на нем пружинным ружьем, неподвижной частью фиксатора с линейкой и ограничителем – 1 шт.
– стойка с физическим маятником – 1 шт.
– цилиндрическая пуля – 1 шт.
Устройство и принцип работы
Установка (рис. 2) состоит из основания 1, стоики 2, на которой закреплена ось физического маятника, состоящего из стержня 3 и ловушки для пули 4. На ловушке установлен неподвижный относительно нее указатель 5 и подвижная часть фиксатора крайнего положения маятника 6. На основании установки закреплены также ограничитель перемещения маятника 7, неподвижная часть фиксатора крайнего положения с измерительной линейкой 8 и пружинное ружье. Пружинное ружье состоит из основания ружья 9, цилиндра с пружиной 10 и рукоятки 11 для сжатия пружины, фиксации ее в сжатом положении и произведения выстрела. Для заряжания ружья цилиндрической пулей в верхней части его основания имеется прямоугольное отверстие 12.
При выводе расчетной формулы рассматривается процесс абсолютно неупругого соударения пули с физическим маятником. Пуля, взаимодействуя с физическим маятником, неупругого тормозится и сообщает маятнику угловую скорость w, в результате маятник отклоняется на угол a от вертикали.
Если время tсоударения пули с маятником мало по сравнению с периодом Т колебания физического маятника, то он за время соударения не успевает заметно отклониться от исходного положения. Учитывая также, что момент внешних сил мал (внешние силы значительно меньше внутренних), систему пуля – маятник можно рассматривать как квазизамкнутую и применять к ней закон сохранения момента импульса.
m1Vl=Iw, (1)
где m1– масса пули, V– скорость пули, l – расстояние от оси маятника до точки попадания в него пули, I – момент инерции маятника с пулей относительно оси вращения физического маятника. В нашем случае
I=(m2l22)/3 + (m1+m3)l12, (2)
где m2– масса стержня, m3– масса ловушки, l2 – длина стержня.
Физический маятник, имея начальную угловую скорость w, отклоняется на угол a (баллистический отброс). При подъеме маятника центр масс поднимается на высоту h. Закон сохранения механической энергии после удара запишется в этом случае в виде
Iw2/2=(m1 + m2 + m3)gh, (3)
где h=Rц.т..(1-cosa)=2Rц.т..sin2(a/2) (4)
– высота подъема центра масс при отклонении маятника;
Rц.т. – расстояние от точки подвеса маятника до центра тяжести системы:
Rц.т.=![]()
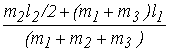 .(5)
.(5)
Выражая Vиз (1), получим
V=wI/m1l1 ,(6)
где w – из (3):
w=(2gh(m1+m2+m3)/I)1/2;(7)
тогда
V=(1/m1l1)(2ghI(m1+m2+m3))1/2 (8)
Подставляя в (8) значения hи I, окончательно получим
V=(2sina/2)/m1ll(g(m2l2/2+m1l1+m3l1)(m2l22/3+m1l12+m3l12))1/2.
Принимая m1=m2m3, а также l1»l2=l,
V = (sina/2)/ m1)((2gl/3)(m22+5m2m3+6m32))1/2. (9)
Так как угол a мал, то можно заменить sin(a/2) = a/2 (при этом угол надо выражать в радианах), где a=(S-S0)/l’, l’ – расстояние от оси вращения маятника до линейки, Scp– среднее значение положения указателя после выстрела и S0 – начальное положение указателя.
Подготовка изделия к работе
1. Закрепить стойку с физическим маятником на основании. При этом обратить внимание на то, чтобы прорезь в подвижной части фиксатора охватывала неподвижную его часть и маятник перемещался по линейке без трения.
2. При необходимости переместить пружинное ружье так, чтобы пуля попадала в центр отверстия ловушки.
Порядок выполнения работы
1.Взвесить на весах пулю и определить ее массу m1.
2.Записать данные установки: m1=...., m2....., m3=...., l=....., l’=....
3.Рукояткой 11 (рис. 2) сжать пружину ружья и зафиксировать ее, повернув рукоятку против часовой стрелки.
4.Подняв подвижную часть фиксатора 6 на ловушке, перевести маятник в вертикальное положение.
5.Записать начальное положение указателя S0.
6.Через прорезь 12 в основании ружья вложить в него цилиндрическую пулю.
7.Произвести выстрел, повернув рукоятку по часовой стрелке.
8.Записать в таблицу положение указателя. Повторить опыт не менее 5 раз.
| № опыта | 1 | 2 | 3 | 4 | 5 | S ср | Scp-So | acp |
S, мм |
9. Определить среднее значение угла aср
aср=(Sср–S0)/lґ.
10. Для каждого значения рассчитать скорость пули V по формуле (9). Значения 1, m1, m2 указаны на установке.
11. Рассчитать погрешность DV/V по формуле
(DV/V)={(Da/a)2+(Dm1/ m1)2+0.25((Dl/l)2+ +((2m2+5m3)2Dm22+ (5m2+12m3)2Dm32) / (m22+5m2m3+m32))}1/2.
Убедиться, что погрешность Dg/g мала по сравнению с остальными относительными погрешностями.
12. Записать окончательный результат в виде
V=(V±DV).
Дополнительное задание: по данным эксперимента определить потери механической энергии при абсолютно неупругом ударе.
Контрольные вопросы
1.Сформулируйте закон сохранения момента импульса и закон сохранения энергии для баллистического маятника.
2.Дайте определение моменту инерции абсолютно твердого тела относительно оси. Каков его физический смысл?
3.Сформулируйте теорему Гюйгенса – Штейнера.
4.Напишите формулу для периода колебаний маятника (математического, физического, пружинного).
5.Объясните суть метода измерения скорости полета снаряда при помощи физического маятника. Получите формулу для скорости снаряда.
6.Увеличится или уменьшится угол отклонения маятника, если удар вместо абсолютного неупругого считать абсолютно упругим? Пояснить.
Лабораторная работа №3
ЛАБОРАТОРНАЯ УСТАНОВКА «МАХОВИК»
Цель работы: лабораторная установка предназначена для иллюстрации законов динамики: второго закона Ньютона и основного уравнения динамики вращательного движения, а также закона сохранения полной механической энергии.
При работе на данной установке определяется момент инерции маховика и оценивается потеря механической энергии на трение.
Приборы и принадлежности: лабораторная установка «Маховик»:
габаритные размеры – не более 400x350x350 мм
масса – не более 30 кг
Состав изделия и комплект поставки:
– маховик со шкивом на подставке – 1 шт.
– груз с нитью – 1 шт.
Устройство и принцип работы
Установка представляет собой горизонтально расположенный вал 1 (рис. 3), закрепленный на основании 2, на котором расположены массивный маховик 3 и два шкива различного диаметра 4. При выполнении лабораторной работы на один из шкивов наматывается нить, на которой закреплен груз 5. Для закрепления нити на шкивах предусмотрены штыри 6.
Момент инерции определяется по результатам измерения времени падения груза с высоты Н. В рабочем положении установка располагается на краю лабораторного стола так, чтобы груз мог опускаться вниз до пола. Для выполнения работы на установке необходимы дополнительные измерительные приборы: штангенциркуль, секундомер и линейка.
Вывод расчетных формул
Для вывода расчетной формулы используем закон изменения полной механической энергии для системы, в которой действуют диссипативные силы: dW = dАдис. Рассматриваемая механическая система состоит из груза массой m и маховика со шкивом и валом с моментом инерции I. В тот момент, когда груз поднят над полом на высоту Н, система обладает потенциальной энергией mgH. При падении груза потенциальная энергия превращается в кинетическую груза и маховика. Изменение полной механической энергии за время падения груза равно работе силы трения:
mv2/2+ Iw2/2 – mgH = А1, (1)
где A1 – работа силы трения за n1 оборотов маховика. Силу трения можно считать постоянной. Тогда движение груза можно считать равноускоренным и описать его уравнениями
v = atH = gt2/2 ;(2)
из этих уравнений получается
v = 2Н/t(3)
угловая скорость вращения маховика
w=2H/rt, (4)
где а – линейное ускорение груза;
v – его скорость непосредственно перед ударом о пол;
w– угловая скорость маховика в тот же момент времени;
t – время падения груза до пола;
r – радиус шкива.
Для определения момента инерции маховика необходимо найти работу силы трения за время падения груза. Если сила трения постоянна, то ее работа пропорциональна числу оборотов маховика. Тогда работу силы трения за время падения груза можно выразить как А1= с1, а работу силы трения от момента соприкосновения груза и пола до полной остановки маховика А2=сn2, где n2 – число оборотов до полной остановки маховика. С другой стороны, А2 равна изменению кинетической энергии маховика 0 – Iw2/2=А2=сn2, откуда получаем
с = Iw2/2n2
и А1 = – 1w2/22 . (5)
Выраженную таким образом работу Ai подставим в равенство (1):
(mv2/2 + Iw2/2) – mgH = – 1Iw2/22.
После замены v и w в соответствии с формулами (3) и (4) получаем значение момента инерции:
I = mr2(gt2 – 2Н)/ 2Н(1 + n1/n2). (6)
Так как r=d/2 и в нашей работе gt2?2H, окончательно получаем:
I=md2gt2/8H(1+1/2). (7)
Порядок выполнении работы
1. Штангенциркулем пять раз измерить диаметры шкивов и записать результаты в таблицу 1.
2. Надеть петлю, имеющуюся на свободном конце нити, привязанной к грузу, на штырь шкива. Вращая маховик, поднять груз на высоту Н. Высоту следует выбрать так, чтобы она соответствовала целому числу оборотов n1. Для этого при нижнем положении груза (груз чуть касается пола, нить натянута) на маховике мелом наносят горизонтальную черту. За этой чертой нужно следить при наматывании нити на шкив.
3.Измерить высоту поднятия груза над полом при помощи вертикально поставленной линейки.
4.Отпустить маховик, одновременно включив секундомер. Остановить секундомер в момент удара груза об пол. Результат записать в таблицу 2.
5.Подсчитать число оборотов 2 от момента удара груза об пол до полной остановки маховика. Опыты 3, 4, 5 повторить 5 раз.
6.Повторить измерения, наматывая нить на другой шкив. Записать результаты в табл. 3.
Таблицы результатов измерений
1. Данные установки: m = (600 ± 1) г.
2. Измерение Н и n1:
при намотке нити на первый шкив: H1 =...., DH1 =..., n11=...,
при намотке на второй шкив: Н2 =..., DH2 =..., n12=....
3. Измерение диаметров шкивов:
Таблица 1
| № опыт | d1 мм | Dd1 мм | d2, мм | Dd2, мм |
| Среднее |
4. Измерение t и 2 для первого шкива:
Таблица 2
| № опыта | t1,c | Dt1, с | 21 | Dn21 |
для второго шкива
Таблица 3
| № опыта | t2, с | Dt2, с | 22 | D22 |
Обработка результатов измерений
1. В конце каждой таблицы рассчитать средние значения измеренных величин и случайные погрешности измерений.
2. По формуле (7) рассчитать момент инерции маховика для измерений с первым и вторым шкивами.
3. Рассчитать погрешность I для одного из случаев по формуле:
(DI/I)2=(Dm/m)2+ 4(Dd/d)2 + 4(Dt/t)2 + (DН/Н)2 +..+(Dn2/n2)2n12/(n1+n2)2.
4. Сравнить результаты расчетов I при работе с первым и вторым шкивами. Дополнительное задания: рассчитать силы натяжения нити, моменты этих сил при работе с первым и вторым шкивами. Показать, что отношение моментов приближенно равно отношению диаметров шкивов и равно отношению ускорений, с которыми движется груз в первом и втором случаях. Определить потери механической энергии при движении груза от верхней точки до момента удара об пол.
Контрольные вопросы
1.Сформулируйте основной закон динамики вращательного движения в дифференциальной форме.
2.Что называется моментом инерции материальной точки и твердого тела относительно оси? В каких единицах он измеряется?
3.От чего зависит значение момента инерции данного тела?
4.Как читается теорема Гюйгенса – Штейнера?
5.Вывести формулу для натяжения нити Т.
6.Какой закон положен в основу вывода рабочей
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Определение эксплуатационных параметров котельной установки Е-500
СодержаниеЗаданиеИсходные данныеОписание котельного агрегата1. Определение расхода топлива по нормативным значениям топлива2. Оп
- Тепловой расчет турбины К-1200-240
- Выключатели высокого напряжения
Выключатели высокого напряженияВыключатель высокого напряжения является основным коммутационным аппаратом в электрических установк
- Схемы конденсационного энергоблока
- История биофизики
Биофизические исследования в физикеИнтерес физиков к биологии в XIX в. непрерывно возрастал. Одновременно и в биологических дисциплина
- Расчет системы электроснабжения
- Наладка электрооборудования
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

