Скачать

Економіко-математичне моделювання процесу ціноутворення на ринку опціонів

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ

УДК 519.866: 336.764.2

ЕКОНОМІКО-МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ

ПРОЦЕСУ ЦІНОУТВОРЕННЯ НА РИНКУ ОПЦІОНІВ

Спеціальність 08.03.08 - економіко-математичне моделювання

АВТОРЕФЕРАТ

дисертації на здобуття наукового ступеня кандидата економічних наук

Сільченко Марина Валеріївна

Київ - 2008

Дисертація є рукописом.

Робота виконана на кафедрі інформатики Київського національного економічного університету Міністерства освіти і науки України.

Науковий керівник - кандидат технічних наук, професор Шарапов Олександр Дмитрович, Київський національний економічний університет, декан факультету інформаційних систем і технологій, завідувач кафедри інформатики.

Офіційні опоненти - доктор економічних наук, професор Вітлінський Вальдемар Володимирович, Київський національний економічний університет, професор, заступник завідуючого кафедрою економіко-математичних методів.

кандидат економічних наук, доцент Краснікова Лариса Іванівна, Національний університет “Києво-Могилянська академія", доцент кафедри фінансів.

Провідна установа - Львівський національний університет ім. Івана Франка Міністерства освіти і науки України, кафедра економічної кібернетики, м. Львів.

Захист відбудеться “13" червня 2008 року о 16 ⁰⁰ годині на засіданні спеціалізованої вченої ради Д 26.066.07 Київського національного економічного університету Міністерства освіти і науки України за адресою: 03680, м. Київ, проспект Перемоги, 54/1, ауд.317.

З дисертацією можна ознайомитись у бібліотеці Київського національного економічного університету за адресою: 03680, м. Київ, проспект Перемоги, 54/1, ауд. 201.

Автореферат розісланий “13" травня 2008 року.

В. о. вченого секретаря спеціалізованої вченої ради Моторин Р.М.

ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОБОТИ

Актуальність теми дослідження. Вихід України на позитивну економічну динаміку вимагає надійного фінансового забезпечення потреб соціально-економічного розвитку. В умовах ринкової економіки, підвалини якої закладені в Україні, основою мобілізації і розміщення фінансових ресурсів є фінансовий ринок. На даний час обидва його сегменти - кредитний ринок та ринок цінних паперів, розвиваються досить складно і нерівномірно. І якщо банківська система, незважаючи на обмежений ресурсний потенціал, в цілому являє собою дієздатний механізм, то ринок цінних паперів по суті знаходиться у стадії формування. Основними проблемами його розвитку є, по-перше, недостатня насиченість ринку відповідними інструментами та обмеженість доступу до нього, і, по-друге, нестабільність ринку.

Основним стабілізуючим чинником на ринку цінних паперів, так як і на товарному та валютному ринках, виступають строкові контракти. Використання похідних цінних паперів - деривативів, дозволяє при розвиненому строковому ринку стабілізувати фінансове положення суб’єктів господарювання та координувати майбутні плани підприємців. Строковий ринок впливає на рівновагу спотового ринку, стимулює розвиток конкуренції на ньому, сприяє оптимальному розміщенню на ньому ресурсів та вирівнюванню цін на різних ринках. Це відбувається завдяки стабілізуючій, інформативній і координуючій функціям, які покладаються на ринок деривативів в економіці. Особливо важливу роль в забезпеченні цих функцій відіграють опціони, які являють собою контракт на майбутню купівлю (або продаж) певного активу за ціною, встановленою при його продажу.

Ринок деривативів у свою чергу може виконувати свої функції і стабілізувати економіку тільки за умови надійного прогнозування цін на опціони. Вирішення цієї задачі можливе лише на підставі поєднання інтуїтивного підходу та економіко-математичних методів. В Указі Президента України щодо основних напрямків розвитку фондового ринку України на 2007 - 2005 рр. зазначено, що технологізація ринків капіталу через зростаюче використання новітніх технологій визначає необхідність створення комплексної системи підготовки фахівців з питань фондового ринку із застосуванням сучасних навчально-методичних технологій та використанням міжнародного досвіду в цій сфері. На підставі цього Указу Державною комісією з цінних паперів та фондового ринку були розроблені програми підготовки фахівців, що включають комплексне вивчення фінансового ринку, зокрема, ринку деривативів, в яке входить його технічний аналіз за допомогою засобів економіко-математичного моделювання.

Проблемам моделювання процесів в економіці і фінансах приділяло увагу багато українських вчених, серед яких Алексєєв А., Бесєдін В., Великий А., Вітлінський В., Геєць В., Єлейко Я., Костіна Н., Лукінов І., Сергієнко І.

Сучасна наука розробила досить надійний апарат визначення справедливої ціни опціону. В дослідженні цієї проблеми вагомим є внесок вітчизняних (Леоненко М., Мішура Ю., Пархоменко В., Ядренко М) та зарубіжних (Мертон Р., Брайен Дж.О., Ширяев А) вчених. Всесвітньо відомими є біноміальна модель Кокса-Росса-Рубінштейна та модель Блека-Шоулза.

Ситуація на сучасних фінансових ринках є мобільною, що призводить до появи нових чинників, які слід вводити в ту чи іншу модель. Зокрема, поява таких учасників ринку, визначення стратегій торгівлі яких здійснюється на базі економіко-математичних моделей з використанням сучасних інформаційних технологій, суттєво впливає на ситуацію на ринку і вимагає відповідного математичного осмислення. Крім того, дуже важливим для успішного розвитку фінансового ринку України є дослідження адекватності існуючих моделей умовам української економіки. При цьому важливо оцінити як надійність вказаних методів, так і їх адаптованість до умов перехідної економіки. Це і визначило вибір теми дослідження.

Зв’язок роботи з науковими програмами, планами, темами. Дисертацію виконано відповідно до плану науково-дослідних робіт кафедри інформатики Київського національного економічного університету за темою: “Теорія і практика побудови великих систем на базі інформаційно-обчислювальних структур” (№ державної реєстрації 0196U023341). В межах даної теми автором досліджено проблеми моделювання фінансово-економічних процесів, зокрема, процесу ціноутворення на ринку опціонів та визначення стратегій хеджування.

Мета та задачі дослідження. Основна мета роботи полягає в розробці економіко-математичних моделей визначення ціни опціону та стратегій його хеджування в умовах насиченого ринку. Для досягнення цієї мети автором були послідовно поставлені наступні завдання:

на підставі аналізу сучасних економічних концепцій щодо місця і функцій ринку строкових контрактів в структурі фінансового ринку, визначити фактори, які впливають на цінові процеси на ринку деривативів;

проаналізувати методи моделювання процесів на фінансовому ринку, зокрема, процесу ціноутворення за строковими контрактами; визначити систему критеріїв, яким повинні задовольняти моделі прогнозування ціни опціону;

побудувати модель, що враховує операційні витрати продавця опціону при виконанні ним хедж-стратегій; дослідити властивості функції ціни опціону, що отримуються з цієї моделі, та з’ясувати, наскільки суттєвим є вплив операційних витрат;

побудувати алгоритм знаходження наближеного аналітичного розв’язку моделі із зворотнім зв’язком у випадку, коли питома вага на ринку програмної торгівлі є значною;

провести числову апробацію можливостей використання моделей прогнозування ціни опціону на фінансовому ринку України.

Об’єктом дослідження є процеси ціноутворення на фінансовому ринку, зокрема, на ринку опціонів.

Предметом дослідження є методологія та інструментарій економіко-математичного моделювання ціноутворення опціонів.

Методи дослідження. При проведенні дисертаційного дослідження методологічним підґрунтям стали комплексні підходи, що базуються на поєднанні фінансово-економічного аналізу та економіко-математичних методів. При вирішенні поставлених завдань використовувались такі методи дослідження, як метод Роте, метод Бубнова-Гальоркіна, метод введення еквівалентних параметрів, методи фінансової математики, методи теорії мартингалів, методи математичного аналізу.

До наукових праць, які склали теоретико-методологічне підґрунтя дисертаційної роботи, відносяться роботи провідних економістів, що дозволяють сформулювати фінансово-економічні засади побудови моделей визначення ціни опціону, та роботи провідних математиків, присвячені проблемам і методології моделювання ринкових процесів, зокрема, процесів на ринку строкових контрактів.

Основним джерелом інформації при виконанні дослідження були статистичні матеріали Міністерства фінансів України, Національного банку України, Державного комітету статистики України, Державної комісії з цінних паперів та фондового ринку, Першої фондової торговельної системи (ПФТС), інформаційно-фінансової системи Reuters.

Наукова новизна одержаних результатів. В процесі комплексного дослідження ринку опціонів засобами, що ґрунтуються на сучасних економічній та математичній теоріях, були отримані наступні положення, які формують наукову новизну роботи:

на підставі систематизації існуючих підходів до структуризації фінансового ринку та запропонованих класифікацій деривативів за типом базового активу та за розподілом ризику, визначено місце строкового ринку в економічній системі країни та виявлені основні чинники, які обумовлюють формування ціни деривативів;

здійснено комплексний аналіз особливостей ціноутворення опціонів, на підставі чого узагальнена система критеріїв, які повинні виконуватись для оцінювання функції ціни опціону і враховуватись при моделюванні цінового процесу;

вдосконалено класичний підхід щодо визначення стратегії хеджування продажу опціону; крім базового активу в структуру хедж-портфелю запропоновано ввести замість облігацій еквівалентний за обсягом банківський кредит;

побудована модель, яка враховує операційні витрати продавця опціону за реалізації ним хедж-стратегій, та знайдено її аналітичний розв’язок - функцію залежності ціни опціону від спот-ціни базового активу, часу, що пройшов від моменту укладання угоди, параметрів опціону та відсотку комісійної винагороди;

запропоновано метод та побудовано ітераційний процес знаходження наближеного аналітичного розв’язку моделі із урахуванням ефекту зворотнього зв’язку, який дозволяє визначити ціну опціону при значній кількості програмних агентів на ринку;

розроблено методику, практичні рекомендації та створено програмний комплекс для використання отриманих теоретичних результатів на фінансовому ринку України при прогнозуванні цін опціонів та визначенні динаміки структури хедж-портфелю.

Практичне значення одержаних результатів полягає в розробці економіко-математичного підґрунтя, програмного комплексу та практичних рекомендацій для визначення справедливої ціни опціону. На підставі отриманих моделей, що враховують додаткові чинники, фахівці та аналітики фондового ринку мають можливість достовірно прогнозувати ситуацію на ринку строкових контрактів, учасники ринку - хеджувати ризики, властиві продажу опціону, та, виявляючи переоцінені та недооцінені опціони, здійснювати арбітражні операції. В зв’язку з тим, що ефективна взаємодія цих агентів є одним із визначальних факторів, які забезпечують виконання ринком своїх функцій, використання запропонованих моделей має відчутне практичне значення в економіці України.

Основні теоретичні та аналітичні результати дисертаційної роботи, побудовані економіко-математичні моделі прогнозування цін на ринку опціонів були впроваджені в роботу казначейства Укрсоцбанку (довідка №05-14/200 від 21.11.2007р) та Державної комісії з цінних паперів та фондового ринку (довідка №12527/18 від 27.11.2007р).

Результати дослідження використовуються також у навчальному процесі Київського національного економічного університету при викладанні дисциплін “Ризик у фінансовому менеджменті" та “Моделювання економіки" (довідка від 11.12.2007р) та дисциплін “Фондовий ринок" та “Ризик у фінансовому менеджменті" у навчальному процесі Українського інституту розвитку фондового ринку Київського національного економічного університету (довідка від 24.10 2007р).

Апробація результатів. Основні результати дисертаційного дослідження доповідались у виступах автора на двох міжнародних науково-практичних конференціях: “Фінансові важелі економічного зростання України на сучасному етапі" (м. Чернівці, Буковинський державний фінансово-економічний інститут, 26-27 жовтня 2006р) та “Ризикологія в економіці та підприємництві” (м. Київ, КНЕУ, 27-28 березня 2007р). Результати та висновки обговорювались також на наукових семінарах кафедри інформатики та кафедри економіко-математичних методів КНЕУта наукових семінарах Українського інституту розвитку фондового ринку КНЕУ.

Публікації. Основні положення, результати та висновки дисертаційного дослідження висвітлено в 6 публікаціях загальним обсягом 2,2 друк. арк., з них 4 статті в наукових фахових виданнях, 2 - тези доповідей на науково-практичних конференціях.

Структура та обсяг дисертації. Відповідно до поставленої мети та визначених завдань дослідження дисертаційна роботаскладається зі вступу, трьох розділів, висновків, списку використаних джерел та додатків. Загальний обсяг дисертації 194 стор. В роботі міститься 11 таблиць на 11 стор., 95 рисунків на 53 стор., 3 додатки на 16 стор. Список використаних джерел налічує 107 найменувань.

ОСНОВНИЙ ЗМІСТ РОБОТИ

У вступі охарактеризовано актуальність теми дослідження в контексті державної програми розвитку фондового ринку в Україні; сформульовано мету та завдання дисертаційної роботи, її наукову новизну та практичне значення; визначено зміст апробації результатів.

У розділі 1 “Дослідження фінансово-економічних засад побудови математичних моделей процесу ціноутворення опціонів” визначено місце ринку строкових контрактів в структурі економіки країни та зв’язки з іншими секторами економіки, в результаті чого виявлені основні економічні чинники, які впливають на процес формування ціни деривативів; обґрунтована необхідність проведення в Україні економіко-математичних досліджень цінових процесів, що відбуваються на ринку строкових контрактів; проаналізовані математичні методи, що дозволяють прогнозувати ціну опціону.

На даний час в українській економічній літературі відображені досить різні погляди вчених на місце ринку строкових контрактів в економічній системі. Багато економістів вважає, що ринок деривативів є сегментом фінансового ринку. Це визначається наступними факторами:

деривативи є предметом торгівлі на фінансовому ринку;

деривативи являють собою контракт, ціна якого формується під впливом попиту і пропозиції;

за організацією свого функціонування деривативи пов’язані з інфраструктурою ринку цінних паперів.

Водночас, в результаті аналізу сутності похідних цінних паперів автором зроблений висновок, що строкові контракти є особливою формою торгівлі. Предметом торгівлі можуть бути як фінансові ресурси (грошові кошти, зокрема, валюта, цінні папери, майбутні ставки за кредитом, і власне деривативи), так і товари та послуги. Тому строковий ринок являє собою надбудову над фінансовим та товарним ринками.

З такого особливого положення строкового ринку в структурі економіки випливає існування прямого та зворотнього зв’язку між процесами, що відбуваються в економіці та процесами на ринку деривативів. Прямий вплив виражається у залежності ціноутворення на строкові контракти від особливостей цінового процесу базового активу, ситуації на кредитному ринку (зокрема, розміру облікової ставки центрального банку), які в свою чергу залежать від загальноекономічної ситуації в країні. Зворотній вплив виражається у виконанні ринком строкових контрактів, особливо ринком опціонів, своїх функцій в економіці: стабілізуючої, координуючої та інформативної. Наявність ефективно функціонуючого строкового ринку є одним із основних факторів, що визначають стабільність економіки в цілому.

Оскільки досягнення економічної стабільності є одним із найважливіших завдань подальшої ринкової трансформації в Україні, в роботі досліджено сучасний стан та перспективи розвитку ринку строкових контрактів в нашій державі. На підставі проведеного аналізу було визначено, що рівень розвитку будь-якого ринку залежить від ступеня насиченості відповідними ресурсами; досконалості нормативно-правової бази; рівню розвитку інфраструктури; достатньої кількості висококваліфікованих учасників ринку.

На даний час в Україні створені відповідна законодавча база та досить розгалужена інфраструктура фінансового ринку, які здатні забезпечити ефективне функціонування ринку деривативів. Проблема насиченості ринку ресурсами буде вирішуватись разом із поглибленням розвитку ринкових відносин в нашій країні. Підготовка ж фахівців із строкового ринку повинна відбуватись вже зараз. Однією з важливих складових їх освіти є оволодіння сучасними методами прогнозування ситуації на ринку, у першу чергу, заснованими на економіко-математичному моделюванні.

Вивчення зарубіжного та вітчизняного досвіду економіко-математичного моделювання привело до висновку, що в умовах ринкової економіки для моделювання цінових процесів переважно використовуються методи фінансової математики, що ґрунтуються на теорії випадкових процесів. Одним з напрямків фінансової математики є дослідження процесу формування цін на деривативи. На підставі дифузійної моделі ринку Ф. Блеком та М. Шоулзом була розроблена модель визначення ціни опціону. Використання отриманих цими вченими результатів при формуванні стратегій хеджування набуло значного поширення серед учасників ринку, що спричинило зворотній вплив на процес ціноутворення опціону.

У розділі 2 “Побудова та дослідження динамічних моделей визначення ціни опціону з урахуванням особливостей програмної торгівлі” досліджені сучасні моделі прогнозування ціни опціону (біноміальна, лог-нормальна, мартингальна, Блека-Шоулза). На підставі проведеного аналізу побудовані моделі, що дозволяють визначити ціну опціону при наявності програмної торгівлі на ринку та операційних витрат, пов’язаних з реалізацією хедж-стратегій продавцем опціону. В процесі дослідження економічних властивостей ціни опціону автором була систематизована, математично сформульована та економічно обґрунтована система обмежень, що накладається на функцію ціни опціону. Зокрема, для ціни європейського опціону на купівлю у випадку, коли за базовим активом не сплачуються дивіденди, мають місце наступні обмеження:

" x≥0, "tÎ (0,T) х − Ke^{−r (T−t)} ≤ C (x,t) ≤ x

де х − ціна базового активу; t − час, що пройшов з моменту укладення опціонної угоди; C (x,t) − функція залежності ціни опціону на купівлю від ціни базового активу x та часу t; T − час дії опціонної угоди, вимірюється в роках; K − ціна реалізації опціону; r − безризикова ставка, що неперервно нараховується.

В основі всіх існуючих моделей визначення ціни опціону лежать припущення щодо відсутності умов для укладання арбітражних угод та можливості формування нейтрального до ризику портфелю, який відображає виплати за опціоном й зміни цін на активи та опціони.

В результаті проведеного порівняльного аналізу сучасних підходів до прогнозування ціни опціону з’ясувалось, що найбільш загальним є підхід, заснований на теорії мартингалів, на основі якого можливо визначати ціну опціону будь-якого типу з будь-якою функцією виплат. На практиці широкого застосування набули модель Блека-Шоулза та її дискретний по часу випадок - біноміальна модель.

Визначення справедливої ціни має важливе значення в опціонній торгівлі. Це пов’язано з багатьма чинниками, в першу чергу з необхідністю виконання ринком строкових контрактів інформативної та координуючої функцій. Крім того, формування стратегій хеджування продажу опціону базується на інформації про майбутню ціну. Особливого значення в сучасних умовах набуло врахування додаткових чинників, які суттєво впливають на адекватність моделі. Тому предметом нашого дослідження стала методологія визначення справедливої ціни опціону із урахуванням особливостей програмної торгівлі.

При дослідженні запропонованих М. Блеком та Ф. Шоулзом методів прогнозування ціни опціону було з’ясовано, що в основі побудови моделі лежало припущення щодо можливості формування хедж-портфелю із базового активу та безризикових облігацій. Зауважимо, що на цьому припущенні базується побудова більшості моделей визначення ціни опціону. При застосування цієї моделі за таких припущень було виявлено, що кількість облігацій в хедж-портфелі завжди є від’ємною величиною. Економічно, від’ємна кількість облігацій в портфелі означає, що в початковий момент треба продати (а не купити) необхідну кількість облігацій, щоб за отримані кошти і опціонну премію купити базовий актив. Оскільки у продавця опціону облігацій для продажу може і не бути, то еквівалентом цієї операції пропонується розглядати отримання банківського кредиту.

Щоб усунути виявлений недолік, автором запропоновано скорегувати базові припущення щодо структури ринку і, відповідно, хедж-портфелю таким чином:

Як і в інших моделях припускається, що на ринку обертаються акції з ціновим процесом {X_t, t≥0}, який підпорядковується рівнянню

dX_t = μX_t dt + σX_t dW_t (1)

де {W_t, t≥0} − стандартний броунівський рух; μ, σ = const, μ − коефіцієнт росту, σ − коефіцієнт волатильності ціни базового активу. Припускається, що Х₀>0 і за акціями не виплачуються ніякі дивіденди при 0 ≤ t ≤ T.

Замість того щоб припускати обіг на ринку безризикових облігацій, автором припускається, що у банку в момент укладання угоди можна отримати довільну кількість кредитів на суму B₀>0 кожний під безризикову ставку r, що неперервно нараховується і є сталою величиною. Позичену суму разом з нарахованими відсотками необхідно повернути наприкінці дії опціонного контракту. Обсяг кредитного боргу B_t в момент часу t становить B₀e^rt.

У відповідності з цією корекцією припускається, що в момент часу t=0 укладається опціонний контракт європейського типу на купівлю однієї акції з ціною реалізації К та строком дії Т; при цьому покупцем опціону виплачується премія С₀, що становить вартість опціону в початковий момент часу. Продавець опціону бере β₀ кредитів на суму B₀ кожний і інвестує отримані за кредитом кошти і премію за опціоном в γ₀ акцій. Таким чином, в початковий момент часу формується портфель π₀ = (β₀, γ₀), такий, що його вартість становить Π₀ = γ₀X₀ − β₀B₀ і дорівнює С₀. Перед продавцем опціону постають два питання: якою має бути премія С₀; якої стратегії хеджування слід дотримуватись при торгівлі цінними паперами, тобто якими мають бути коефіцієнти β_t і γ_t в кожний момент часу дії опціонного контракту, щоб вартість портфеля π_t, сформованого на основі цієї премії та з цими траекторіями коефіцієнтів хеджування, в момент часу Т дорівнювала виплатам по опціону, тобто Π_T≡ γ_TX_T- β_TB_T= max{0, x− K}.

На підставі запропонованих автором припущень та з урахуванням обмежень на ціну опціонну отримана модель, яка співпадає з моделлю Блека-Шоулза:

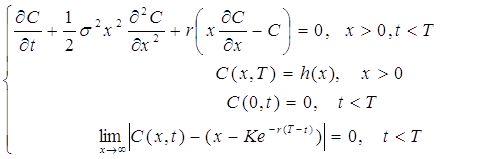(2)

Її точний розв’язок має вигляд:

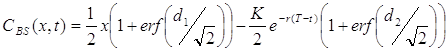(3)

де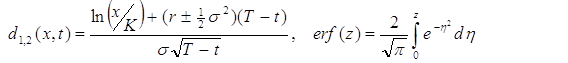

Проте структура хедж-портфелю у відповідності із зробленою корекцією змінюється таким чином: в кожний момент часу t необхідно тримати портфель, у якому буде β (Х_t,t) кредитів та γ ₍Х_t, t) акцій, де Х_t − ціна акції в момент часу t, і функції β та γ визначаються за формулами:

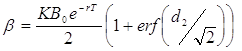(4)

Легкість та ефективність застосування на практиці результатів, отриманих Ф. Блеком та М. Шоулзом, обумовило появу на ринку програмної торгівлі, тобто торгівлі деривативами, хеджування яких відбувається за допомогою формування портфелю із структурою, що розраховується за формулами, аналогічними формулам (4).

Аналіз особливостей ведення програмної торгівлі показує, що існують деякі проблеми, які не враховані в класичній моделі Блека-Шоулза - проблема операційних витрат та наявності ефекту зворотнього зв’язку. Перша проблема пов’язана з тим, що при реалізації стратегій хеджування, тобто при динамічній зміні кількості базового активу у хедж-портфелі, продавець опціону має певні операційні витрати (маржа, комісійні, податки). На основі аналізу характеру їх оплати зроблено висновок, що найбільш впливовими є комісійні, які сплачуються посередникам за операції купівлі-продажу базового активу на ринку і становлять певний відсоток від суми транзакції. З урахуванням умови сплати комісійних у розмірі λ відсотків, автором отримано наступну модель визначення ціни опціону:

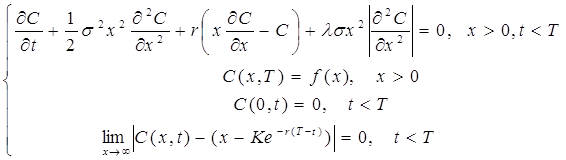(5)

та знайдено її точний розв’язок:

(6)

тобто

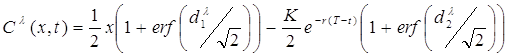(7)

де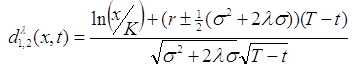

Відповідні стратегії хеджування обчислюються за формулами, аналогічними формулам (4).

Проведене в роботі дослідження характеру впливу операційних витрат на вартість опціону дозволило зробити наступні висновки. Було з’ясовано, що при відсутності операційних витрат, тобто при λ= 0, ціна опціону може розраховуватись за формулою Блека-Шоулза (3). Врахування майбутніх операційних витрат призводить до збільшення початкової премії за опціон і, як наслідок, зростає ціна опціону в кожний момент часу. Чим більшими є операційні витрати, тим більшою є ціна опціону.

Також досліджувалось питання, настільки суттєвим є вплив операційних виплат на ціну опціону. Це питання зводиться до оцінки функції Δ (x,t) =C^λ (x,t) −C_BS (x,t) та характеру її залежності від параметрів. Максимальне значення по t функція Δ (x,t) набуває при t=0 при будь-яких фіксованих значеннях параметрів T, K, r, σ, λ:

max{Δ (x,t), tÎ (0, Т) }=Δ (x,0)

Тому замість оцінки функції Δ (x,t) оцінювалась функція δ^λ (x): =Δ (x,0).

В результаті автором були встановлені, математично доведені і економічно обґрунтовані наступні закономірності:

Зростання волатильності базового активу σ спричиняє збільшення впливу операційних витрат на ціну опціону, тобто

для будь-яких фіксованих значень Т, K, r, λ.

Зростання самих операційних витрат λ призводить до збільшення їх впливу на ціну опціону, тобто

для будь-яких фіксованих значень Т, K, r, σ. Зменшення безризикової ставки спричиняє зростання впливу операційних втрат і вплив операційних втрат є найбільшим, коли ставка дорівнює нулю, тобто

для будь-яких фіксованих значень Т, K, σ, λ.

Збільшення ціни реалізації K приводить до збільшення впливу операційних витрат, тобто

для будь-яких фіксованих значень Т, r, σ, λ.

При збільшенні строку дії Т опціонного контракту при невеликих значеннях безризикової ставки r вплив операційних витрат зростає, тобто

для будь-яких фіксованих значень K, σ, λ.

Виявлені закономірності свідчать, що вплив операційних витрат є вагомим і їм не можна нехтувати, особливо враховуючи те, що при великих обсягах торгівлі навіть невеликі значення корекцій C^λ −C_BS суттєво впливають на кінцевий результат. Тому запропонована автором модель має важливе значення для правильної оцінки опціону, оскільки враховує ціну виконання продавцем опціону хеджуючих стратегій і, таким чином, дозволяє знизити ризики, пов’язані з продажем опціону.

Інша проблема, пов’язана з програмною торгівлею, викликана появою ефекту зворотнього зв’язку. Модель, що враховує наявність на ринку програмної торгівлі, була отримана К. Сіркаром та Дж. Папаніколау:

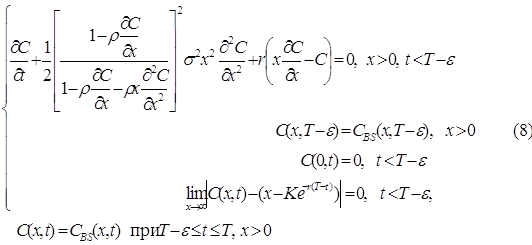
де ρ - питома вага програмних торговців на ринку, ε - коефіцієнт згладжування, що знаходиться з наступного рівняння:

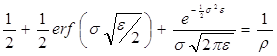
Наведена нелінійна кінцево-крайова задача немає точного розв’язку.

В дисертації запропоновано метод знаходження наближеного аналітичного розв’язку при довільному значенні питомої ваги програмної торгівлі, який базується на комбінації методів Роте та Бубнова-Гальоркіна.

Ідея методу знаходження наближеного аналітичного розв’язку полягає в розбитті часу дії опціону на рівних частин.

На кожному і-ому часовому шарі наближений розв’язок шукається у вигляді:

а відповідні коефіцієнти А_і з умови, щоб нев’язка

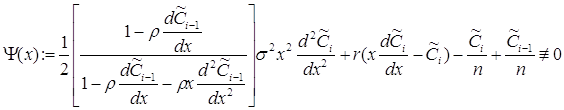
задовольняла наступну умову:

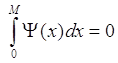
M>0 - деяке достатньо велике число, яке залежить від К, і таке, що C (x,t) =C_BS (x,t) = x-Ke^{-r (T-t)} при х ≥ М.

Отримані формули для знаходження коефіцієнтів А_і дозволяють знаходити значення ціни опціону на будь-якому часовому шарі.

В результаті проведеного дослідження було з’ясовано, що наявність на ринку програмної торгівлі спричиняє зростання ціни опціону і чим більшою є питома вага програмних торгівців, тим більший ефект зворотнього зв’язку. Зауважимо, що оскільки в нашій країні ринок строкових контрактів лише формується, на ньому ще немає торговців цінними паперами, які б вели програмну торгівлю, тобто ρ=0. В розвинених країнах відсоток цих торговців є значним і тому, як показують отримані результанти, їм не можна нехтувати.

У розділі 3 “Реалізація розроблених моделей ціноутворення з використанням сучасних інформаційних технологій” проілюстровані закономірності, властиві процесу ціноутворення для опціонів з різними параметрами, та проведена числова апробація запропонованих моделей на прикладі фондових і валютних опціонів, які використовуються на фінансовому ринку України.

Побудовані графіки відображають основні властивості функції ціни опціону та дозволяють проводити якісний аналіз цінових процесів, які відбуваються на ринку опціонів. Отримані емпіричні результати підтверджують теоретичні висновки, зроблені у розділі 2, надають уявлення про характер впливу параметрів опціону на процес ціноутворення і на формування хедж-портфелю та дозволяють використовувати при розрахунках метод номограми.

В основу дослідження покладено європейський опціон на купівлю однієї акції з наступними параметрами: K_s= 5, r_s= 0.04, Т_s = 0.5, σ_s = 0.4. На рис.1 представлений графік функції C_BS та γ_BS для опціону Ō_s = {σ_s, r_s, K_s, T_s}.

Рис.1. Графіки функцій C_BS та γ_BS для опціону Ō_s

Цей рисунок ілюструє, що функція C_BS є монотонно зростаючою по х. При t = Т графік ціни опціону є ламаною лінією − графіком функції max{0, x − K}; з наближенням до t = 0 графік згладжується, проте його характер не змінюється. Аналіз впливу зміни параметрів опціону на функцію C_BS свідчить, що загальна поведінка функції не змінюється. Графіки функцій C^λ та Ĉ і подібні до графіка C_BS і лежать вище нього. Рис.2 та рис.3 ілюструють вплив операційних витрат та програмної торгівлі на ціну опціону.

Рис.2. Графік різниці функцій C^λ і C_BS при λ =0,01 ₍2.1) та його перетини при t₁=Т/4, t₂=Т/2, t₃=3Т/4 (2.2)

Аналіз рис.2 підтверджує властивості, аналітично отримані у розділі 2:

ціна опціону, яка враховує майбутні витрати, завжди більша за ціну опціону, розраховану за формулою Блека-Шоулза.

операційні витрати спричиняють найбільший вплив на зростання ціни опціону в момент укладання угоди. З часом вплив операційних витрат зменшується.

Аналогічним чином на ціну опціону впливає наявність на ринку програмної торгівлі, про що свідчить рис.3.

Рис.3. Графіки різниці функцій Ĉ і C_BS при ρ =0,01та при t₁=Т/4 (3.1), t₂=Т/2 (3.2), t₃=3Т/4 (3.3)

Результати отримані за допомогою програмного комплексу, розробленого автором в математичному редакторі Mathematica3.0.

З метою з’ясування можливості використання на фінансовому ринку України моделей прогнозування ціни опціону в роботі проведена числова апробація отриманих результатів.

У якості прикладу були розглянуті два типи опціонів:

фондовий опціон: базовий актив - акції Центренерго, ціна базового активу - найкраща ціна акції за день;

валютний опціон: базовий актив - американський долар, ціна базового активу - курс гривні щодо долара США.

У якості ціни реалізації приймалось майбутнє значення ціни базового активу, спрогнозоване на основі попередніх даних. На рис.4 наведені графіки, які ілюструють динаміку цін на базовий актив і опціон і визначаються за допомогою формули (7) при λ = 5% для одного з валютних опціонів.

Рис.4. Динаміка курсу гривні щодо долара США та ціни валютного опціону.

При дослідженні впливу операційних витрат, були проведені підрахунки суми комісійних, які повинен сплачувати продавець опціону. З’ясувалось, що початкова премія за опціон, яка була розрахована на підставі скорегованої моделі, перевищує суму сплачених комісійних та премії, розрахованої за формулою Блека-Шоулза, тобто вона з незначним перебільшенням враховує майбутні комісійні.

З метою виявлення характеру впливу програмної торгівлі були побудовані порівняльні графіки функцій, розрахованих за існуючими формулами Блека-Шоулза і Сіркара-Папаніколау та за формулою, запропонованою автором. Отримані результати ілюструють, що врахування ефекту зворотнього зв’язку приводить до значного збільшення ціни опціону. Причому, чим більше значення параметра ρ, тим більш відчутним є цей вплив. З наближенням дати реалізації опціону цей вплив стає менш відчутним і наприкінці дії опціону він зникає.

ВИСНОВКИ

В дисертації проведено комплексне дослідження процесу формування ціни на ринку опціонів, що базується на поєднанні фінансового та економіко-математичного аналізу. Розроблені методи дозволяють визначати ціну опціону і, відповідно, стратегію хеджування ризиків за наявності операційних витрат та програмної торгівлі. Результати вирішення поставлених у дисертації завдань дозволяють зробити наступні висновки:

Аналіз сучасних підходів щодо визначення місця ринку деривативів в структурі фінансового ринку свідчить, що це питання потребує подальшого осмислення в економічній науці. На думку автора, цей ринок можна одночасно вважати як частиною фінансового ринку, так і надбудовою над товарним і всіма секторами фінансового ринку. Тому, з одного боку, механізми та закони функціонування ринку строкових контрактів пов’язані з фінансовим ринком, а, з іншого боку, ситуація на ринку деривативів впливає на ситуацію на товарному та фінансовому ринках, а звідси, на всю економіку взагалі.