Дослідження процесів масопереносу при фільтрації підземних вод
дипломний проекту на тему:
“ Дослідження процесів масопереносу при фільтрації підземних вод ”.
Івано-Франківськ
2008 р.
Зміст
Вступ
1.Моделювання й прогнозування якості підземних вод
1.1. Математичне моделювання динаміки забруднення підземних вод
1.1.1.Конформні перетворення й моделювання масопереносу при фільтрації підземних вод
1.1.2. Моделювання конвективної дифузії розчинених речовин при профільній фільтрації
1.1.3.Моделювання масопереносу у випадку D=D(![]() ) при наявності масообміну
) при наявності масообміну
1.1.4. Моделювання процесів забруднення підземних вод з урахуванням якості поверхневих вод
1.2. Методи прогнозування (водойми)
2. Рішення крайових задач (лінійних) математичної фізики
2.1. Моделювання
3. Прогнозування якості підземних вод
3.1.Основні фізичні закони фільтрації підземних вод
3.1.1. Закон Дарсі
3.2. Постановка крайових завдань плоскої фільтрації
3.3. Зв'язок рівнянь плоскої фільтрації з теорією функцій КЗ
3.4. Метод конформних відображень у теорії фільтрації
3.4.1.Спосіб Павловського
3.4.2.Спосіб Ведерникова-Павловского
3.5. Конформні перетворення й моделювання масопереносу
3.6. Крайові задачі конвективної дифузії розчинених речовин при профільній фільтрації
3.6.1. Крайові й початкові умови для шуканої функції с(х, у, t) :
3.6.2. Перший тип крайових задач
3.6.3. Другий тип крайових задач
4. Отримання аналітичних розв'язків при конвективній дифузії солей і гіпсів
5. ОХОРОНА ПРАЦІ
5.1 Організація робочого місця
5.2 Захист від електромагнітних випромінювань та електростатичних полів
5.3 Електробезпека
5.4 Пожежна профілактика
Список використаної літератури
Вступ
Сучасне виробництво продукції характеризується зростанням масштабів випуску, розмежовуванням технологічних і виробничих функцій, ускладненням технологічних об'єктів (для підвищення якості продукції) і зв'язків між ними, зростанням числа функцій управління і питомої ваги вартості систем управління в загальних капітальних витратах на устаткування.
Зростання потреби як в кількісних, так і в якісних показниках виробництва, з одного боку, і виникнення нових технологічних процесів і можливості їхнього здійснення, з другого боку, приводять до значних ускладнень як самих технологічних об'єктів, так і зв'язків між ними, і численними додатковими функціональними пристроями, покликаними забезпечити якнайкраще в якомусь сенсі функціонування цих об'єктів.
Поява нових технологічних процесів (ТП), їхня інтенсифікація є результатом науково-технічного прогресу не тільки в даній конкретній області, але пов'язані з комплексними досягненнями в різних областях науки і техніки. Нові технологічні об'єкти, наприклад, в нафтохімії створюються на основі знайдених нових закономірностей отримання продукту і вимагають застосування нових конструкційних матеріалів, методів їхньої обробки, зварки, збірки, транспортування, нових видів реактивів, каталізаторів и.т.п.
Виникнення нових і інтенсифікація існуючих ТП відбувається безперервно, і швидкість цих процесів може служити одній з характеристик технічного прогресу.
Технологічні процеси представляють собою первинну ланку створення матеріальних цінностей, вони забезпечують виробництво необхідною для існування суспільства продукції.
1. Моделювання й прогнозування якості підземних вод
1.1. Математичне моделювання динаміки забруднення підземних вод
1.1.1. Конформні перетворення й моделювання масопереносу при фільтрації підземних вод
Процес міграції розчинних речовин при фільтрації підземних вод, як відомо, описується наступною системою рівнянь.
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
або в скалярній формі
![]() (1.4)
(1.4)
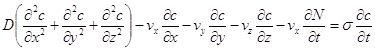 ; (1.5)
; (1.5)
![]() (1.6)
(1.6)
де ![]() - вектор швидкості фільтрації, м/сут;
- вектор швидкості фільтрації, м/сут; ![]() - потенціал фільтрації;
- потенціал фільтрації; ![]() і
і ![]() - концентрація речовини, що дифундує, відповідно в рідкій і твердій фазах, г/см3; D - коефіцієнт конвективної дифузії, м3/сут; σ - активна (або ефективна) пористість середовища, у якій відбувається фільтрація розчину; t - час у добі;
- концентрація речовини, що дифундує, відповідно в рідкій і твердій фазах, г/см3; D - коефіцієнт конвективної дифузії, м3/сут; σ - активна (або ефективна) пористість середовища, у якій відбувається фільтрація розчину; t - час у добі; ![]() - оператор Гамильтона;
- оператор Гамильтона; ![]() - константа швидкості масообміну; β - коефіцієнт розподілу речовини між фазами в умовах рівноваги по лінійній изотермі Генрі cp = βN .
- константа швидкості масообміну; β - коефіцієнт розподілу речовини між фазами в умовах рівноваги по лінійній изотермі Генрі cp = βN .
У багатьох практичних завданнях можна обмежитися вивченням процесу масопереносу розчинних у фільтраційному потоці речовин тільки на основі рівнянь, що описують конвективний процес, а саме:
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
причому масообмін визначається наступною досить розповсюдженою залежністю:
![]() (1.9)
(1.9)
де ![]() - концентрація граничного насичення.
- концентрація граничного насичення.
Наведені рівняння описують, як правило, міграцію й фізичну трансформацію (сорбцію, десорбцію) консервативних водорозчинних речовин.
Якщо досліджувати масоперенос при плоско-вертикальній і планової сталій або квазиустановленій фільтрації підземних вод, то до моделювання даного процесу доцільно застосувати конформне перетворення рівнянь масопереносу до криволінійним змінних - координатам крапок області комплексного потенціалу фільтрації.
У випадку плоско-вертикальної (профільної) фільтрації рівняння руху підземних вод запишуться у вигляді
![]() (1.10)
(1.10)
де χ - коефіцієнт фільтрації, h - напір, що визначається рівністю
![]() (1.11)
(1.11)
причому вісь Oy спрямована вертикально вниз, p - тиск, ρ - щільність, g - прискорення сили ваги.
У випадку планової напірної фільтрації відповідні рівняння записуються в такий спосіб:
![]()
![]() (1.12)
(1.12)
а у випадку планової безнапірної фільтрації
![]()
![]() (1.13)
(1.13)
У рівняннях (1.12), (1.13) через T позначена потужність напірного водоносного шару: ![]() - вектор питомої фільтраційної витрати (м2/сут), a h - напір, у цьому випадку визначається наступним рівнянням:
- вектор питомої фільтраційної витрати (м2/сут), a h - напір, у цьому випадку визначається наступним рівнянням:
![]() , (1.14)
, (1.14)
де Z - вертикальна координата крапки фільтраційного потоку.
Припускаючи, що для розглянутих фільтраційних плинів можна побудувати область комплексного потенціалу ![]() , де ψ- функція потоку, і що відомо характеристичну функцію течії
, де ψ- функція потоку, і що відомо характеристичну функцію течії
![]() (1.15)
(1.15)
за допомогою заміни
![]() (1.16)
(1.16)
перетворимо рівняння конвективної дифузії до нових незалежних змінних ![]() й
й ![]() . У результаті такої заміни рівняння конвективної дифузії у випадку плосковертикальної фільтрації запишеться у вигляді
. У результаті такої заміни рівняння конвективної дифузії у випадку плосковертикальної фільтрації запишеться у вигляді
![]() (1.17)
(1.17)
у випадку планової напірної фільтрації - у такому виді
![]() (1.18)
(1.18)
а у випадку планової безнапірної фільтрації перетвориться до наступного виду:
![]() (1.19)
(1.19)
Поставивши в рівняннях (1.17)-(1.19) D= 0, одержимо рівняння конвективного масопереносу без обліку дифузійних процесів, перетворені до новим змінних ![]() ,
, ![]() або Φ, Ψ,, або Φ*, Ψ* відповідно для випадків плоско-вертикальної, планової напірної й планової безнапірної фільтрації, а саме:
або Φ, Ψ,, або Φ*, Ψ* відповідно для випадків плоско-вертикальної, планової напірної й планової безнапірної фільтрації, а саме:
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
![]() (1.22)
(1.22)
Таким чином, у випадку знехтування дифузійними процесами питання про визначення концентрації речовин, що забруднюють підземні води, зводиться до рішення відповідного фільтраційного завдання й одного з рівнянь (1.20)-(1.22) при одній додатковій (початковій) умові, що задається залежно від фізичної постановки завдання.
Важливою характеристикою при дослідженні процесу забруднення підземних вод є час, протягом якого в даній точці області ![]() (або області z)концентрація розчинної речовини досягає певної величини. Крім того, виникає також питання про визначення часу, протягом якого концентрація розчинної речовини досягає в даній точці максимального значення. Основні диференціальні рівняння, з яких визначаються ці характеристики, а також фронт просування речовини (домішок) у фільтарционному потоці будуть наведені нижче.
(або області z)концентрація розчинної речовини досягає певної величини. Крім того, виникає також питання про визначення часу, протягом якого концентрація розчинної речовини досягає в даній точці максимального значення. Основні диференціальні рівняння, з яких визначаються ці характеристики, а також фронт просування речовини (домішок) у фільтарционному потоці будуть наведені нижче.
Нехай відома концентрація розчинного у фільтраційному потоці речовини як функції координат точок області комплексного потенціалу ![]() й часу t . Тоді для кожного значення (моменту) часу t можна побудувати поверхня розподілу концентрації щодо області комплексного потенціалу
й часу t . Тоді для кожного значення (моменту) часу t можна побудувати поверхня розподілу концентрації щодо області комплексного потенціалу![]() , а отже, і щодо області фільтрації z . Тим самим для кожного моменту часу буде визначене значення концентрації речовини, що поширюється в підземних водах, у будь-якій точці області фільтрації або уздовж лінії, що цікавить нас, зокрема, уздовж кожної з ліній потоку або еквіпотенціальних ліній.
, а отже, і щодо області фільтрації z . Тим самим для кожного моменту часу буде визначене значення концентрації речовини, що поширюється в підземних водах, у будь-якій точці області фільтрації або уздовж лінії, що цікавить нас, зокрема, уздовж кожної з ліній потоку або еквіпотенціальних ліній.
Якщо ж припустити, що міграція речовини відбувається з постійною концентрацією, то час, протягом якого відбудеться забруднення певної частини області фільтрації, знайдемо в такий спосіб. Нехай відома швидкість фільтрації v(x,y,t) і характеристична функція плину, отримана у вигляді (1.16). Швидкість поширення розчинного у фільтраційному потоці речовини U(x,y,t) у цьому випадку дорівнює дійсній швидкості руху підземних вод V(x,y,t) , яка зв'язана зі швидкістю фільтрації v(x,y,t) співвідношенням
![]() (1.23)
(1.23)
де через ![]() позначена активна пористість ґрунту (породи). При миттєво протікаючих сорбіційних процесах, що визначаються рівністю (1.9), активна пористість заміняється так називаною ефективною пористістю середовища, обумовленої рівністю
позначена активна пористість ґрунту (породи). При миттєво протікаючих сорбіційних процесах, що визначаються рівністю (1.9), активна пористість заміняється так називаною ефективною пористістю середовища, обумовленої рівністю
![]() (1.24)
(1.24)
З (1.23) одержуємо
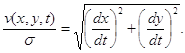 (1.25)
(1.25)
Після перетворення рівності (1.25) до нових незалежних змінних ![]() й
й ![]() маємо
маємо
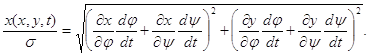 (1.26)
(1.26)
Замість рівнянь (1.20)-(1.22) зручно розглядати рівняння
![]() (1.27)
(1.27)
де ![]() - безрозмірні величини, причому
- безрозмірні величини, причому ![]() . До рівняння (1.27) можна легко звести кожне з рівнянь (1.20)-(1.22). Дійсно, якщо в рівнянні (1.27) покласти
. До рівняння (1.27) можна легко звести кожне з рівнянь (1.20)-(1.22). Дійсно, якщо в рівнянні (1.27) покласти
![]()
то одержимо рівняння (1.20), якщо в рівнянні (1.27) покласти
![]()
то одержимо рівняння (1.21), а якщо в рівнянні (1.27) покласти
![]()
те одержимо рівняння (1.22).
Математичні моделі міграції
Зупинимося тепер на математичних моделях міграції (поширення) у фільтраційних потоках неконсервативних забруднюючих речовин (домішок). Неконсервативність такої домішки породжується їхньою взаємодією в результаті різних хімічних і біохімічних перетворень. Тому математична модель таких хімічних і біохімічних взаємодій будується за допомогою системи диференціальних рівнянь щодо концентрації кожної з речовини, що вступає в реакцію.
У підземні води можуть попадати й інші неконсервативні речовини, які добре взаємодіють із киснем, що втримується в підземних водах. Тому, якщо концентрацію неконсервативної речовини позначити через cнв, а концентрацію розчиненого в підземних водах кисню - cРК, то поширення таких речовин у підземних водах можна описати наступною системою рівнянь:
![]()
![]() (1.28)
(1.28)
![]()
![]() (1.29)
(1.29)
![]() (1.30)
(1.30)
![]() (1.31)
(1.31)
Члени рівнянь, що містять функцію ![]() , описують кінетику хімічної або біохімічної взаємодії (окислювання хімічної речовини або деструкцію органічної речовини за рахунок подиху мікроорганізмів). Опис цієї взаємодії представляє досить складне завдання. Однак для такого опису можна використати деякі закони хімічної кінетики. Зокрема, якщо скористатися законом діючих мас, то дана взаємодія буде описуватися відповідно до кінетики ізотермічної бімолекулярної реакції
, описують кінетику хімічної або біохімічної взаємодії (окислювання хімічної речовини або деструкцію органічної речовини за рахунок подиху мікроорганізмів). Опис цієї взаємодії представляє досить складне завдання. Однак для такого опису можна використати деякі закони хімічної кінетики. Зокрема, якщо скористатися законом діючих мас, то дана взаємодія буде описуватися відповідно до кінетики ізотермічної бімолекулярної реакції
![]() (1.32)
(1.32)
де зазвичай ставлять m = n = 1.
У практиці математичного моделювання використовуються й більш прості кінетичні залежності, зокрема, можна використати систему рівнянь Стритера - Фелпса:
![]() (1.33)
(1.33)
![]() . (1.34)
. (1.34)
У випадку значного перевищення концентрації кисню над концентрацією забруднюючої речовини (малі концентрації забруднення) можна використати ще більш прості залежності, а саме
![]() (1.35)
(1.35)
або
![]() (1.36)
(1.36)
Для моделювання динаміки неконсервативної речовини до рівнянь (1.28)-(1.31) необхідно додати початкові й граничні умови, потім відшукати аналітичне, числено-аналітичне або чисельне рішення відповідної крайової задачі. Зокрема, крайова задача для моделювання динаміки БПК (органіки, що окисляєлегко) і РК (розчиненого кисню) при плоско-вертикальній фільтрації підземних вод записується в такому виді:
![]() (1.37)
(1.37)
![]() (1.38)
(1.38)
![]() (1.39)
(1.39)
![]() (1.40)
(1.40)
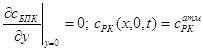 (1.41)
(1.41)
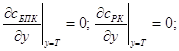 (1.42)
(1.42)
![]() (1.43)
(1.43)
![]() (1.44)
(1.44)
1.1.2. Моделювання конвективної дифузії розчинених речовин при профільній фільтрації
Процес масопереносу розчинних у підземних водах речовин описується системою диференціальних рівнянь у частинних похідних другого порядку зі змінними коефіцієнтами, яка у випадку двовимірної плоско-вертикальної (профільної) сталої фільтрації підземних вод за умови сталості коефіцієнта конвективної дифузії має такий вигляд:
![]() (1.45)
(1.45)
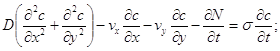 (1.46)
(1.46)
![]() (1.47)
(1.47)
де D - коефіцієнт конвективної дифузії в м![]() /сут, c й N - концентрація речовин, що дифундують, у г/л або кг/м
/сут, c й N - концентрація речовин, що дифундують, у г/л або кг/м![]() відповідно в рідкій і твердій фазах; vx(x, y, t)і vy(x, y, t) - координати вектора швидкості фільтрації в м/сут; σ - пористість або активна пористість ґрунту, у якому відбувається рух вод і конвективная дифузія розчинної речовини; α - постійна масообміну (швидкості сорбції); c0 - початкова концентрація речовини в рідкій фазі; β - коефіцієнт розподілу речовини між рідкою й твердою фазами в умовах рівноваги за законом лінійної ізотерми Генрі, що виражається рівністю cp = βN, причому через cp позначена рівноважна концентрація розчину, по величині рівна кількості речовини, що поглинає твердою фазою;
відповідно в рідкій і твердій фазах; vx(x, y, t)і vy(x, y, t) - координати вектора швидкості фільтрації в м/сут; σ - пористість або активна пористість ґрунту, у якому відбувається рух вод і конвективная дифузія розчинної речовини; α - постійна масообміну (швидкості сорбції); c0 - початкова концентрація речовини в рідкій фазі; β - коефіцієнт розподілу речовини між рідкою й твердою фазами в умовах рівноваги за законом лінійної ізотерми Генрі, що виражається рівністю cp = βN, причому через cp позначена рівноважна концентрація розчину, по величині рівна кількості речовини, що поглинає твердою фазою; ![]() -потенціал швидкості фільтрації; χ - коефіцієнт фільтрації в м/сут;
-потенціал швидкості фільтрації; χ - коефіцієнт фільтрації в м/сут; ![]() - напір в м; -тиск у
- напір в м; -тиск у
Н(м2 =кг/м·c2 ); ρ - щільність у кг/м3; g - прискорення сили ваги в м/с2.
Розглянемо конвективну дифузію тих розчинних речовин, які нейтральні до наявних у ґрунті породам, тобто надалі сорбцією й іншими видами поглинання забруднюючі підземні води компонентів знехтуємо й будемо виходити з наступної системи рівнянь фільтрації й конвективної дифузії (гідравлічної дисперсії):
![]() (1.48)
(1.48)
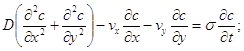 (1.49)
(1.49)
При конвективній дифузії речовин, що забруднюють підземні води, на вході АВ фільтраційного потоку можна прийняти одне з наступних граничних умов:
а) задана концентрація розчиненого у водоймі (ріці) речовини
![]() (1.50)
(1.50)
б) задана умова Данквертса, що враховує як конвективний, так і дифузійний механізми відводу речовини на водопроникній ділянці границі області фільтрації
![]() (1.51)
(1.51)
де - нормаль до границі; vn - нормальна складова швидкості фільтрації.
На водонепроникних ділянках границі області фільтрації й на криві депресії виконується умова
![]() (1.52)
(1.52)
На ділянці виходу фільтраційного потоку (CD) можна приймати одне з наступних граничних умов:
а)задана концентрація речовини, що дифундує, або задана умова Данквертса (такі умови приймаються, якщо не спостерігається інтенсивного відводу вод на виході фільтраційного потоку)
![]() (1.53)
(1.53)
б) задана умова, що враховує тільки конвективний перенос через границю (у випадку інтенсивного відводу вод на виході фільтраційного потоку)
![]() (1.54)
(1.54)
При конвективній дифузії солей і гіпсів, що залягають на певній глибині T фільтраційного потоку, на границі із сіллю або гіпсом звичайно приймається умова
![]() (1.55)
(1.55)
де ![]() - концентрація повного насичення солі або гіпсу.
- концентрація повного насичення солі або гіпсу.
Початкові умови засолення підземних вод, мають вигляд
![]() (1.56)
(1.56)
де c0 - задана концентрація речовини, що дифундує, в області фільтрації в момент часу до настання процесу забруднення (засолення) або промивання підземного середовища.
Трудність, що виникає при рішенні стаціонарних і нестаціонарних крайових завдань, що описують двовимірні процеси, зв'язана не тільки з видом рівнянь у частинних похідних і з видом граничних умов, а головним чином з видом (геометрією) області, у якій відшукується рішення. У зв'язку із цим у рівняннях конвективної дифузії й у наведених вище граничних умовах доцільно перейти до нових незалежних змінних координат комплексного потенціалу ω, що, як відомо, має вигляд багатокутника зі сторонами, паралельними прямокутній системі координат.
Нехай відома характеристична функція течії
![]() (1.57)
(1.57)
яку можна знайти, наприклад, методом конформних відображень. Тоді, зробивши в рівнянні конвективної дифузії (1.49) заміну змінних ![]() й
й ![]() одержимо наступне рівняння.
одержимо наступне рівняння.
Взявши середню величину ![]() , щовходить у праву частину рівняння (1.49) по області наведеного комплексного потенціалу
, щовходить у праву частину рівняння (1.49) по області наведеного комплексного потенціалу ![]() , і заміняючи її деякою середньою величиною
, і заміняючи її деякою середньою величиною ![]() , розглянемо два типи нестаціонарних крайових завдань.
, розглянемо два типи нестаціонарних крайових завдань.
Перший тип крайових завдань виникає при фільтрації забруднених вод у відкриті водойми (водоймища), коли в останні підтримується задана концентрація речовин. Ці задачі формулюються в такий спосіб: потрібно знайти рішення ![]() рівняння
рівняння
![]() (1.58)
(1.58)
задовольняючій або граничній умовам виду (перша задача)
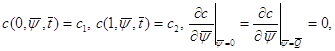 (1.59)
(1.59)
або умовам, що враховують механізм дифузійного відводу речовини від границі на вході фільтраційної течії (друга задача):
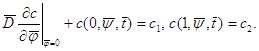 (1.60)
(1.60)
і початковій умові
![]() (1.61)
(1.61)
Безпосередньою перевіркою легко переконатися, що рішенням двовимірних крайових завдань (1.58), (1.59), (1.61) і (1.58), (1.60), (1.61) будуть функції ![]() й
й ![]() , щоє рішеннями відповідних одномірних крайових завдань:
, щоє рішеннями відповідних одномірних крайових завдань:
![]() (1.62)
(1.62)
![]() (1.63)
(1.63)
![]() (1.64)
(1.64)
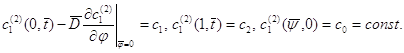 (1.65)
(1.65)
Підставляючи це рішення у вигляді суми рішень стаціонарного й нестаціонарного завдань і застосовуючи метод поділу змінних, одержимо рішення нестаціонарних завдань конвективної дифузії, які після розподілу на c1 і введення безрозмірних величин ![]() і
і ![]() запишуться в наступному вигляді.
запишуться в наступному вигляді.
![]() (1.66)
(1.66)
![]() (1.67)
(1.67)
де власні значення ![]() й
й ![]() визначаються рівняннями
визначаються рівняннями
![]() (1.68)
(1.68)
![]() (1.69)
(1.69)
Коефіцієнти ![]() й
й ![]() обчислюються за формулами
обчислюються за формулами
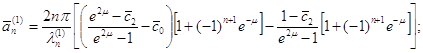 (1.70)
(1.70)
![]() (1.71)
(1.71)
Другий тип крайових задач конвективної дифузії підземної води, речовин що забруднять, характеризується гарничною умовою, що приймається на виході фільтраційного потоку, коли спостерігається інтенсивний відвід із дренажного каналу CD. У цьому випадку рішенням стаціонарних задач буде стала, значення якої залежить від крайової умови на вході фільтраційного потоку.
Тому перейдемо до розгляду нестаціонарних завдань. Осереднюючи швидкість фільтрації по просторовим змінним, приходимо до наступних двох крайових завдань: Потрібно знайти рішення ![]() рівняння
рівняння
![]() (1.72)
(1.72)
задовольняючим крайовим умовам:
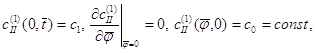 (1.73)
(1.73)
а у випадку обліку механізму дифузійного відводу речовини на вході фільтраційного потоку (друга крайова задача) потрібно знайти вирішення ![]() рівняння
рівняння
![]() (1.74)
(1.74)
задовольняючим крайовим умовам:
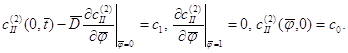 (1.75)
(1.75)
Застосування методу Фур'є до крайової задачі(1.72)-(1.73) дає вирішення
![]() (1.76)
(1.76)
де ![]() , функція
, функція ![]() визначається рівностями
визначається рівностями
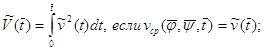 (1.77)
(1.77)
![]() (1.78)
(1.78)
Коефіцієнти ![]() обчислюються по наступній формулі:
обчислюються по наступній формулі:
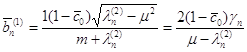 . (1.79)
. (1.79)
Рішення крайової задачі (1.74)-(1.75) одержуємо в наступному виді:
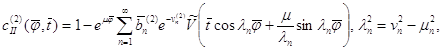 (1.80)
(1.80)
де коефіцієнти ![]() обчислюються по формулі
обчислюються по формулі
![]() (1.81)
(1.81)
а власні значення λn визначаються з рівняння
λn =![]() (1.82)
(1.82)
Замість власних значень λn можна шукати значення v![]() = λ
= λ![]() + µ2 з рівняння
+ µ2 з рівняння
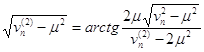 (1.83)
(1.83)
Таким чином, отримані аналітичні рішення всіх основних крайових завдань конвективної дифузії, забруднюючих воду, речовин за умови осереднення швидкості фільтрації по просторових координатах.
1.1.3. Моделювання масопереносу у випадку D=D(![]() ) при наявності масообміну
) при наявності масообміну
Вихідні рівняння. Процес масопереносу розчинних речовин (солей, гіпсів й ін.) при фільтрації підземних вод можна описати наступною системою диференціальних рівнянь у частинних похідних:
![]() (1.84)
(1.84)
![]() (1.85)
(1.85)
![]() (1.86)
(1.86)
де ![]() - вектор швидкості фільтрації;
- вектор швидкості фільтрації; ![]() - потенціал швидкості фільтрації; χ - коефіцієнт фільтрації;
- потенціал швидкості фільтрації; χ - коефіцієнт фільтрації; ![]() - дифузійний потік або вектор масової швидкості розчиненої речовини (вектор кількості речовини, що переноситься через одиницю площадки за одиницю часу);
- дифузійний потік або вектор масової швидкості розчиненої речовини (вектор кількості речовини, що переноситься через одиницю площадки за одиницю часу); ![]() і
і ![]() - концентрації речовини відповідно в рідкій і твердій фазах;
- концентрації речовини відповідно в рідкій і твердій фазах; ![]() - коефіцієнт конвективної дифузії (Dm- коефіцієнт молекулярної дифузії), σ - активна (або ефективна) пористість середовища;
- коефіцієнт конвективної дифузії (Dm- коефіцієнт молекулярної дифузії), σ - активна (або ефективна) пористість середовища; ![]() - оператор Гамільтона, α - постійна швидкості масообміну; β- коефіцієнт розподілу речовини між фазами в умовах рівноваги при лінійній ізотермі Генрі
- оператор Гамільтона, α - постійна швидкості масообміну; β- коефіцієнт розподілу речовини між фазами в умовах рівноваги при лінійній ізотермі Генрі
![]() (1.87)
(1.87)
де Γ - коефіцієнт Генрі.
У багатьох практичних задачах як рівняння кінетики масообміну береться одне з наступних рівнянь.
1) при кристалізації або розчиненні компонентів породи у фільтрівній воді
![]() (1.88)
(1.88)
де ![]() -коефіцієнт насичення:
-коефіцієнт насичення:
2) при нерівномірній необоротній сорбції або десорбції відповідно
![]() (1.89)
(1.89)
3) при рівноважній сорбції або десорбції відповідно
![]() (1.90)
(1.90)
![]() (1.91)
(1.91)
де ![]() (або
(або![]() ) - так звана ефективна пористість або масооб’єм поглинання (виділення) речовини породою.
) - так звана ефективна пористість або масооб’єм поглинання (виділення) речовини породою.
Надалі як рівняння кінетики беремо рівняння (1.88), що є в математичному відношенні найбільш загальним з наведених вище. Тому у випадку плоско-вертикальної сталої фільтрації система рівнянь масопереносу запишеться у вигляді
![]() (1.92)
(1.92)
![]() (1.93)
(1.93)
Припустимо, що вирішено фільтраційне завдання й визначений комплексний потенціал фільтрації ![]() як деяка аналітична функція
як деяка аналітична функція ![]() . Тоді область комплексного потенціалу
. Тоді область комплексного потенціалу ![]() буде конформно відображатися на область фільтрації z функцією
буде конформно відображатися на область фільтрації z функцією
![]() (1.94)
(1.94)
названою зазвичай характеристичною функцією течії (![]() - функція потоку). Доцільно перетворити рівняння конвективної дифузії (1.93) за допомогою заміни (1.94) до нових незалежних змінних
- функція потоку). Доцільно перетворити рівняння конвективної дифузії (1.93) за допомогою заміни (1.94) до нових незалежних змінних ![]() й
й ![]() . При такому конформному перетворенні варто враховувати прийняте припущення про залежність коефіцієнта конвективної дифузії Dyвід швидкості фільтрації v. Крім того, варто взяти до уваги, що величина коефіцієнта конвективної дифузії Dyзалежить не тільки від величини швидкості фільтрації, але й від її напрямку як тензор, і при рішенні крайових завдань конвективної дифузії, як правило, швидкість фільтрації осереднюється або по всій області комплексного потенціалу, або по одній з координат точок цієї області.
. При такому конформному перетворенні варто враховувати прийняте припущення про залежність коефіцієнта конвективної дифузії Dyвід швидкості фільтрації v. Крім того, варто взяти до уваги, що величина коефіцієнта конвективної дифузії Dyзалежить не тільки від величини швидкості фільтрації, але й від її напрямку як тензор, і при рішенні крайових завдань конвективної дифузії, як правило, швидкість фільтрації осереднюється або по всій області комплексного потенціалу, або по одній з координат точок цієї області.
У зв'язку із цим доцільно робити осереднення коефіцієнта конвективної дифузії в новій системі координат окремо уздовж еквіпотенциальних ліній й уздовж лінії струму. Тим самим уводиться поняття коефіцієнта поперечної конвективної дифузії D![]() і коефіцієнта поздовжньої конвективної дифузії D
і коефіцієнта поздовжньої конвективної дифузії D![]() . Таким чином, у результаті перетворення рівняння (1.93) до нових змінних одержимо
. Таким чином, у результаті перетворення рівняння (1.93) до нових змінних одержимо
![]() (1.95)
(1.95)
Якщо ввести безрозмірні величини
![]()
то рівняння (1.95) запишеться у вигляді
![]() (1.96)
(1.96)
де H - діючий напір.
Одержання рішення при осереднені швидкості фільтрації.
При вивченні процесів міграції промислових або побутових стічних вод, що скидають у водойму, а також при розрахунку виносу ядохімікатів або добрив із сільськогосподарських угідь, розглянутих у вигляді смуги певної ширини, виникає необхідність визначення якісного складу підземних вод, ступеня їхнього забруднення або мінералізації. Рішення всіх цих важливих питань зводиться до розгляду відповідних крайових завдань фільтрації й конвективної дифузії, фільтраційні задачі для яких розглянуті вище.
Будемо вирішувати крайову задачу конвективної дифузії при осереднені швидкості фільтрації по всій області комплексного потенціалу ![]() , потім розглянемо випадок осереднення швидкості фільтрації по одній з координат області комплексного потенціалу
, потім розглянемо випадок осереднення швидкості фільтрації по одній з координат області комплексного потенціалу ![]() або
або ![]() . Опускаючи риски над безрозмірними величинами в рівнянні (1.96), в області
. Опускаючи риски над безрозмірними величинами в рівнянні (1.96), в області ![]() шукаємо рішення рівняння
шукаємо рішення рівняння
![]() (1.97)
(1.97)
де
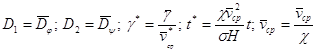
при наступних граничних і початкових умовах:
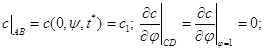 (1.98)
(1.98)
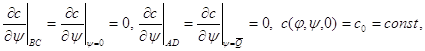 (1.99)
(1.99)
причому через c1 позначена концентрація речовини у водоймі АВ, а через c0 - концентрація речовини в підземних водах у початковий момент часу t0 = 0 . Рішення крайової задачі (1.97)-(1.99) будемо шукати у вигляді
![]() (1. 100)
(1. 100)
де функція ![]() знаходиться як рішення стаціонарної задачі
знаходиться як рішення стаціонарної задачі
![]() (1. 101)
(1. 101)
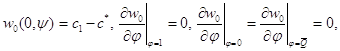 (1. 102)
(1. 102)
а функція ![]() знаходиться в результаті рішення нестаціонарної крайової задачі
знаходиться в результаті рішення нестаціонарної крайової задачі
![]() (1. 103)
(1. 103)
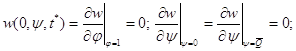 (1. 104)
(1. 104)
![]() (1. 105)
(1. 105)
Функція, що задовольняє рівнянню (1.101) і граничним умовам (1.102), не залежить від змінної ψ, а крайова задача (1.101),(1.102) еквівалентна наступній:
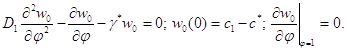 (1. 106)
(1. 106)
Вирішивши крайову задачу, знайдемо
![]() (1. 107)
(1. 107)
де
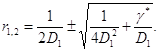
Розглянемо тепер задачу
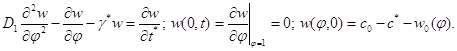 (1. 108)
(1. 108)
Загальна схема методу Фур'є. Рішення крайової задачі шукаємо у вигляді ![]() . Підставивши це рішення в (1.108), одержимо:
. Підставивши це рішення в (1.108), одержимо:
![]() (1. 109)
(1. 109)
Із цієї рівності, з огляду на граничні умови, приходимо до задачі на власні значення
![]() (1. 110)
(1. 110)
Загальне рішення цього рівняння має вигляд
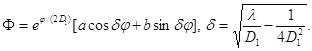 (1. 111)
(1. 111)
Використовуючи граничні умови, одержимо рівняння для визначення всіх власних значень задачі.
![]()
з якого після перетворення й введення величини 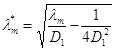 одержуємо рівняння для визначення всіх власних значень
одержуємо рівняння для визначення всіх власних значень
![]() (1. 112)
(1. 112)
Шукані власні функції запишуться у вигляді
![]() (1. 113)
(1. 113)
Тоді
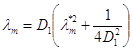 . (1.114)
. (1.114)
З рівності (1.109) для кожного λm одержуємо рівняння
![]() (1. 115)
(1. 115)
рішення якого має вигляд
![]() (1. 116)
(1. 116)
З огляду на (1.113) і (1.116), записуємо часткові рішення вихідного крайової задачі у вигляді
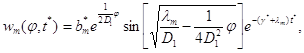 (1. 117)
(1. 117)
а шукане рішення крайової задачі (1.105), (1.106) у силу узагальненого принципу суперпозиції запишеться у вигляді
![]() (1. 118)
(1. 118)
Використовуючи початкові умови, знаходимо коефіцієнти ![]() у вигляді
у вигляді
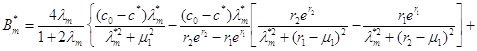
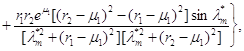 (1. 119)
(1. 119)
де r1, r2 визначаються рівностями (1.104), а µ1= 1/(2D1) .
Таким чином, рішення вихідної крайової задачі (1.97)-(1.99) у випадку осереднення швидкості фільтрації по всій області комплексного потенціалу ω не залежить від ψ і має такий вигляд:
![]() (1. 120)
(1. 120)
Якщо у виразах (1.119),(1.120) покласти γ* = 0, c* = 0, r1 = 0 , r2 = =1/D1= 2µ1 = 2µ, то одержимо рішення задачі про забруднення підземних вод без обліку масообміну, розглянуте раніше, а саме:
![]() (1. 121)
(1. 121)
де
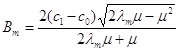 (1. 122)
(1. 122)
Моделювання процесу очищення (промивання) засолених земель
Нехай промивання засолених земель відбувається в результаті поливу прісною водою поверхні ґрунту й відводу вод за допомогою одиночної дрени або за допомогою системи дрен. У цьому випадку для кожної з фільтраційних схем, що зустрічаються, область комплексного потенціалу зображується у вигляді прямокутника.. Тому питання вивчення процесу промивання підземного середовища зводиться до рішення в прямокутнику ABCD наступної крайової задачі.
![]() (1.123)
(1.123)
![]() (1. 124)
(1. 124)
Бачимо, що ця крайова задача збігається із крайовою задачею (1.97)-(1.99), якщо покласти c1 = 0 , c0 = cн, а отже, рішення задачі (1.123) -(1.124) виходить із рішення (1.122), якщо c1 = 0 , c0 = cн.
Конвективная дифузія у випадку планової фільтрації
Розглянемо такі схеми руху підземних вод, коли виконуються відомі передумови гідравлічної теорії фільтрації. Тоді у випадку сталої або квазіустановленої планової фільтрації рівняння руху підземних вод запишуться у вигляді
![]() (1. 125)
(1. 125)
а у випадку планової безнапірної фільтрації - у вигляді
![]() (1. 126)
(1. 126)
де T - потужність напірного водоносно шару, q - вектор питомої фільтраційної витрати (м2/сут), a h - напір, що у випадку, коли вісь апплікат спрямована вертикально вниз, визначається рівністю
![]() (1. 127)
(1. 127)
Припускаючи, що для кожного із плинів відома область комплексного потенціалу ω і функція, що відображає (1.94)
![]() (1. 128)
(1. 128)
перетворимо тривимірне рівняння конвективної дифузії, що у розглянутих випадках має вигляд
![]() (1. 129)
(1. 129)
до нових змінних за допомогою підстановки
![]() (1. 130)
(1. 130)
Тоді у випадку планової напірної фільтрації рівняння конвективної дифузії перетвориться до виду
![]() (1. 131)
(1. 131)
а у випадку планової безнапірної фільтрації до такому виду
![]() (1. 132)
(1. 132)
При осереднені величини ![]() по області комплексного потенціалу ω питання про дослідження міграції водорозчинних речовин зводиться до відшукання в прямокутному паралелепіпеді ωЧT (або ω Ч hcp)рішення наступної крайової задачі.
по області комплексного потенціалу ω питання про дослідження міграції водорозчинних речовин зводиться до відшукання в прямокутному паралелепіпеді ωЧT (або ω Ч hcp)рішення наступної крайової задачі.
![]() (1. 133)
(1. 133)
![]() (1. 134)
(1. 134)
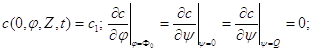 (1. 135)
(1. 135)
![]() (1. 136)
(1. 136)
Крайова задача (1.133) (1.136) еквівалентна крайовій задачі типу (1.97)-(1.99), а тому її рішення, що не залежить від ψ від Z , запишеться у вигляді (1.120). При цьому варто врахувати, що замість безрозмірних величин (1.98) варто ввести безрозмірні величини, які визначаються іншими рівностями окремо для випадку напірної й безнапірної планової фільтарції. Якщо ж розглядається процес засолення підземних вод, що відбувається в результаті дифузії залягаючих на глибині T* солей, то замість крайових умов (1.136) необхідно взяти наступні:
![]() (1. 137)
(1. 137)
Рішення крайової задачі (1.133)-(1.135), (1.136) можна одержати тільки за допомогою чисельних методів, а у випадку, коли величина питомої фільтраційної витрати осереднюеться тільки по одній зі змінних ![]() або ψ, рішення відповідних крайових задача можна знайти за допомогою методу Фур'є в сполученні з варіаційними методами.
або ψ, рішення відповідних крайових задача можна знайти за допомогою методу Фур'є в сполученні з варіаційними методами.
1.1.4. Моделювання процесів забруднення підземних вод з урахуванням якості поверхневих вод
При проектирвании й експлуатації басейнів стічних вод різного призначення (ставків - відстійників, ставків - накопичувачів, ставків - охолоджувачів, хвосто - і шламосховищ) виникає необхідні
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Екологічна безпека мастильно-охолоджувальних рідин
Міністерство освіти і науки УкраїниЧернігівський державний педагогічний університет імені Т.Г. ШевченкаЗаочне відділенняКафедра екол
- Екологічна оцінка природних умов басейну річки Рудка (Волинська область)
- Екологічна оцінка стану довкілля Коростишивського району та розробка заходів з його поліпшення
Тема дипломного проекту«Екологічна оцінка стану довкілля Коростишивського району та розробка заходів з його поліпшення»РЕФЕРАТОб’єк
- Екологічний стан р. Південний Буг. Характеристика та заходи щодо його поліпшення
Кваліфікаційна роботаЕкологічний стан р. Південний Буг. Характеристика та заходи щодо його поліпшенняВступВ умовах науково-технічного
- Екологічні аспекти видобування піску на прикладі об`єктів Чернігівської області
ЗмістВступ1. Загальна характеристика будівельної промисловості2. Скляна промисловість2.1 Історія виробництва2.2 Сировина2.3 Класифікація
- Екологічні проблеми сільськогосподарського виробництва
ЗМІСТВступ1. Екологічні особливості агроекосистем2. Антропогенний тиск на агроекосистеми3. Основні напрямки екологічної стабілізації а
- Екологія рідких тварин України
Міністерство Аграрної Політики УкраїниТаврійська Державна Агротехнічна АкадеміяКафедра: Екологія та охорона навколишнього середовищ
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

