Скачать

Дифференциальная геометрия поверхностей Каталана

Содержание

Глава 1.Введение в дифференциальную геометрию поверхностей. Основные понятия

1.1 Первая квадратичная форма поверхности

1.2 Внутренняя геометрия поверхности

1.3 Вторая квадратичная форма поверхности

1.4 Классификация точек регулярной поверхности

1.5 Средняя и гауссова кривизны поверхности

Глава 2. Понятие поверхности Каталана

2.1 Общие положения

2.2 Примеры поверхностей Каталана

2.3 Виды поверхностей Каталана

Глава 3. Дифференциальная геометрия поверхностей Каталана

3.1 Первая и вторая квадратичные формы линейчатой поверхности

3.2 Первая и вторая квадратичные формы поверхности Каталана

3.3 О коноидах

Глава 4. Специальные поверхности Каталана (поверхности класса КА)

4.1 Вывод уравнения поверхности класса КА

4.2 Вывод уравнения поверхности класса КА по заданным кривым и нормальному вектору порождающей плоскости

Глава 5. Дифференциальная геометрия поверхностей класса КА

5.1 Первая и вторая квадратичные формы линейчатой поверхности

5.2 Первая квадратичная форма поверхности класса КА

5.3 Вторая квадратичная форма поверхности класса КА

Глава 6. О программе визуализации и анализа поверхностей

6.1 Общие положения и возможности программы

6.2 Примеры работы

Выводы

Список литературы

Глава 1. Введение в дифференциальную геометрию поверхностей.

Основные понятия

1.1 Первая квадратичная форма поверхности

Пусть  - гладкая поверхность,  – ее векторное параметрическое уравнение и .

Определение 1.1.

Первой квадратичной формой на поверхности  называется выражение

                                                                                                          (1)

Распишем это выражение подробнее.

,

Откуда                                                               (2)

Выражение (2) в каждой точке поверхности  представляет собой квадратичную форму от дифференциалов  и . Первая квадратичная форма является знакоположительной, так как ее дискриминант

 и .

Для коэффициентов первой квадратичной формы часто используют следующие обозначения (и мы в своих исследованиях будем придерживаться именно их) ((1).(2),(3)):

,

,

.

Так что выражение (2) для формы  можно переписать в виде

                                                                                (3)

Соответственно,

.

1.2 Внутренняя геометрия поверхности

Известно, что, зная первую квадратичную форму поверхности, можно вычислять длины дуг кривых на поверхности, углы между кривыми и площади областей на поверхности. В самом деле, если рассмотреть формулы, определяющие вышеуказанные величины, можно заметить, что туда входят только лишь коэффициенты , ,  первой квадратичной формы. Поэтому если известная первая квадратичная форма поверхности, можно исследовать геометрию на поверхности, не обращаясь к ее уравнениям, а лишь используя ее первую квадратичную форму.

Совокупность геометрических фактов, относящихся к поверхности, которые можно получить при помощи ее первой квадратичной формы, составляет так называемую внутреннюю геометрию поверхности.

Поверхности, имеющие одинаковые первые квадратичные формы и потому имеющие одинаковую внутреннюю геометрию, называются изометричными.

Рассмотрим простой пример.

Пусть задана поверхность

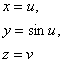
Это цилиндрическая поверхность с синусоидой в качестве направляющей.

Имеем:

,

Поэтому

,

,

Следовательно,

.

Если сделать замену, вводя новые параметры  и  таким образом

,

.

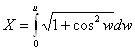Тогда первая квадратичная форма поверхности примет, очевидно, вид

.

Мы видим, что в новых переменных первая квадратичная форма рассматриваемой цилиндрической поверхности совпадает с первой квадратичной формой плоскости  и поэтому внутренняя геометрия этой поверхности совпадает с внутренней геометрией плоскости. Т.е. синусоидальный цилиндр изометричен плоскости. Этот важный факт мы еще получим несколько другим способом.

Чисто геометрически это свойство понятно: синусоидальный цилиндр получается изгибанием (т.е. деформацией без сжатий и растяжений) обычной плоскости. При такой деформации внутренняя геометрия не изменяется.

Более того, можно показать, что если одна поверхность получается из другой путем изгибания, то внутренние геометрии этих поверхностей совпадают.

1.3 Вторая квадратичная форма поверхности

1.3.1. Определение второй квадратичной формы.

Основным объектом рассмотрения в этой части изложения станет  - регулярная поверхность , заданная своим радиус-вектором.

,

В каждой точке такой поверхности помимо единичного вектора нормали

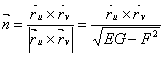                                                                                (1)

Определен и второй дифференциал радиус вектора

                                                 (2)

Определение 1.2.

Второй квадратичной формой поверхности  называется скалярное произведение векторов  и .

 ((1),(3),(4),(5))                      (3)

Нетрудно заметить, что в каждой точке поверхности  квадратичная форма (3) является квадратичной формой относительно дифференциалов  и .

Для коэффициентов второй квадратичной формы приняты (и мы также в дальнейшем будем пользоваться этим) следующие обозначения

                                                                                                  (4)

Это позволяет записать ее в следующем простом виде

                                                                             (5)

Покажем еще один способ вычисления коэффициентов второй квадратичной формы поверхности.

Заменим в формулах (4) единичный вектор нормали  на его выражение (1), получим,

                                                                                            (6)

Для подробного вывода нужно знать тождество:

.

Продолжим рассуждения.

Так как векторы  и  ортогональны (первый, разумеется лежит в касательной плоскости к поверхности, а второй лежит в плоскости нормального сечения).

Поэтому

.

Откуда

Отсюда, дифференцируя, получим:

                                                                                          (7)

Это дает еще один способ расчета второй квадратичной формы.

((5),(6))                (8)

Отсюда же можно получить новые формулы для вычисления коэффициентов второй квадратичной формы. Впрочем, удобнее продифференцировать по  и по  очевидные равенства

 и .

Воспользовавшись соотношениями (4), получаем, что

                                                                                    (9)

Вторая квадратичная форма эффективна при выяснении графических свойств регулярной поверхности.

1.4 Классификация точек регулярной поверхности

Пусть  – регулярная поверхность и  – ее параметрическое задание.

Выберем на поверхности  некоторую точку  и рассмотрим плоскость , которая касается поверхности  в этой точке.

Отклонение произвольной точки  поверхности  от плоскости  определим по формуле

                                                                                      (1)

В этой формуле  – единичный вектор нормали к поверхности в точке . Это отклонение, взятое по абсолютной величине, равно расстоянию от точки  до плоскости . Отклонение положительно, если точка  и конец вектора  лежат по одну сторону от касательной плоскости, соответственно, оно отрицательно, если они лежат по разные стороны от касательной плоскости в точке .

Рассмотрим формулу (1).

Разность  допускает следующую интерпретацию

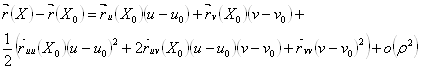                           (2)

Где

, при .

Умножим обе части равенства (2) скалярно на вектор  и положив

, .

Получим, что

                                                           (3)

Разумеется, вдумчивый (или хотя бы немного читающий эти выкладки) читатель поймет, что коэффициенты

,

,

указанные в формуле (3) вычислены в точке , в окрестности которой мы и рассматриваем исходную поверхность .

Из курса линейной алгебры известно, что свойства квадратичной формы во многом определяются ее дискриминантом. А скорее даже знаком квадратичной формы.

Вычислим дискриминант второй квадратичной формы в точке .

Рассмотрим все возможные случаи.((7),(8),(9),(10),(11))

Случай 1.

Т.е. вторая квадратичная форма поверхности в заданной точке является знакоопределенной.

Зафиксируем в точке  некоторое направление на поверхности. Пускай .

Тогда любое другое направление на поверхности в точке  можно задавать при помощи угла , который оно образует с уже выбранным направлением.

Положим

,

Тогда

                                                  (4)

Нетрудно показать, что

,

где постоянная

а в силу условия

 положительна.

Таким образом неравенство

выполняется независимо от выбора угла .

Так как порядок стремления к нулю при  второго слагаемого  в правой части формулы (3) выше двух, то из последней оценки можно сделать следующий вывод.

Отклонение  сохраняет знак (совпадающий со знаком второй квадратичной формы ) для всех достаточно малых значений независимо от выбора направления на поверхности.

Это означает, что все точки поверхности , достаточно близкие к точке , располагаются по одну сторону от касательной плоскости поверхности в этой точке. Такая точка поверхности называется эллиптической точкой.

Например, все точки сфер – эллиптические.((6),(8))

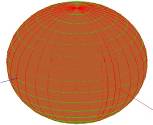
Случай 2.

.

Вторая квадратичная форма является знакопеременной.

Покажем, что в этом случае, в точке  можно указать два неколлинеарных направления на поверхности, обладающие следующими свойствами:

- для значений дифференциалов, определяющих эти направления, вторая квадратичная форма поверхности, вычисленная в точке , обращается в нуль,

- все остальные направления на поверхности в точке  разбиваются на два класса – для дифференциалов, определяющих направления одного из этих классов, вторая квадратичная форма положительна и для другого отрицательна.

Пусть некоторое направление  положительного класса задается углом . В соответствии с формулой (4) имеем

, ((1),(4),(11))

где

Как видно из формулы (3), знак отклонения  для всех достаточно малых значений  в рассматриваемом направлении  совпадает со знаком второй квадратичной формы . Следовательно, если точка  поверхности  достаточно близка к точке , то это отклонение положительно.

Рассуждая аналогично, можно указать точки на поверхности, близкие к точке , для которых отклонение  будет отрицательным.

Приведенные рассуждения показывают, что вблизи точки  поверхность  располагается по разные стороны от касательной плоскости. При этом проекции точек поверхности, отклонения которых расположены на касательный плоскости заполняются множество «между» этими направлениями…

В этом случае точка называется гиперболической точкой поверхности.

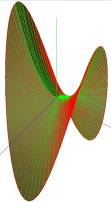
Случай 3.

.

Но отличен от нуля хотя бы один из коэффициентов, , .

Пусть для определенности . Тогда вторая квадратичная форма поверхности  в точке  может быть записана в следующем виде

Тем самым в зависимости от знака  форма  либо неотрицательна, либо неположительна. При этом на поверхности  в точке  можно указать направление , такое, что определяющие его дифференциалы  и  обращают вторую квадратичную форму  в нуль.

Для всех других направлений на поверхности в точке  форма имеет один и тот же знак (совпадающий со знаком )

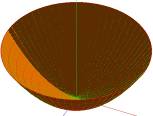
В этом случае точка  называется параболической точкой поверхности .

Случай 4. ((1),(11),(12))

Такая точка  называется точкой уплощения поверхности. Расположение поверхности, близ таких точек может быть самым разнообразным.

Например, все точки плоскости являются точками уплощения.

1.5 Средняя и гауссова кривизны поверхности

Нам осталось рассмотреть еще немного понятий, прежде чем приступить к исследованиям. Рассмотрим на поверхности  произвольную  - регулярную кривую, проходящую через точку  в направлении .

Пусть

- естественная параметризация кривой. Вычислим в точке  три вектора

- единичный вектор касательной к кривой

,

- единичный вектор нормали к поверхности

- и вектор

Эта тройка векторов линейно независима. Это позволяет представить вектор

в виде линейной комбинации

Так как , то

.

Коэффициенты  и  имеют специальные названия.

 – нормальная кривизна кривой

 – геодезическая кривизна кривой.

Примем без доказательства следующую формулу для вычисления нормальной кривизны поверхности в заданном направлении

                                                                             (1)

Как видно из этой формулы нормальная кривизна поверхности в данной точке зависит от направления на поверхности.

Определение 1.3.

Направление на поверхности называется главным, если нормальная кривизна в этом направлении достигает экстремального значения.

Покажем, что в каждой точке -регулярной поверхности найдется не мене двух различных главных направлений.

Пусть  – произвольное направление в точке  на поверхности . Тогда

                                                                                  (2)

(2) – дифференцируемая функция переменных  и . Отметим, что функции коэффициентов второй и первой квадратичных форм определяются только выбором точки  и от переменных  и  не зависят.

Полагая

,

получим, что

Так как функция

 непрерывна и , то на отрезке  она либо постоянна, либо имеет хотя бы один максимум. Это и означает, что в каждой точке  - регулярной поверхности есть два различных главных направления.

Определение 1.4.

Экстремальные значения нормальных кривизн в главных направлениях называются главными кривизнами поверхности в данной точке.

Укажем способ вычисления главных кривизн в данной точке регулярной поверхности.

Из формулы (2) вытекает тождество относительно переменных  и

                                                        (3)

Продифференцируем это тождество по . Учитывая, что производная нормальной кривизны в главном направлении обращается в нуль, получим для главного направления

                                                                              (4)

                                                                             (5)

Здесь  – главная кривизна в направлении .

Рассматривая полученные соотношения (4) и (5) как систему линейных алгебраических уравнений относительно неизвестных  и , получим, что эта система всегда имеет ненулевое решение, так как в данной точке регулярной поверхности всегда есть главные направления.

Из этого вытекает, что

Вычисляя определитель, мы получим квадратное уравнение для искомой функции  (внимание… мы его будем использовать при некоторых выкладках далее).

                                                (6)

Возможны два случая.

Случай 1.

Квадратное уравнение имеет два различных корня  и .

Этим корням на поверхности соответствует два различных главных направления.

Случай 2.

Уравнение (6) имеет один корень кратности 2 .

Это могут быть только точки уплощения  или омбилические точки (точки округления) ().

Определение 1.5.

Средней кривизной  поверхности в данной точке называется полусумма ее главных кривизн в этой точке.

                                                                                               (7)

Определение 1.6.

Гауссовой кривизной  поверхности называется произведение ее главных кривизн.

                                                                                                        (8)

В виду уравнения (6) можно показать, что

                                                                                  (9)

                                                                                              (10)

Этих основных понятий нам пока хватит для рассмотрения специального класса поверхностей.

Глава 2. Понятие поверхности Каталана

2.1 Общие положения

Определение 2.1.

Поверхность Каталана – линейчатая поверхность, прямолинейные образующие которой параллельны одной и той же плоскости.

Определение 2.2.

Плоскость, которой параллельны образующие поверхности Каталана, называется плоскостью параллелизма.

Определение 2.3.

Поверхность Каталана, все образующие которой пересекают одну прямую, называется Коноидом.

Замечание 2.1.

Обычно предполагают, что уравнение поверхность Каталана:

, причем .

Мы, однако, не будем учитывать это условие, а ограничимся указанным выше определением. И те, и другие поверхности мы будем для краткости называть поверхностями Каталана.

Замечание 2.2.

Из определения поверхности Каталана следует, что, если ее уравнение:

, то .

Это очевидно, так как все три вектора (вычисленные при одном и том же значении параметра), участвующие в смешанном произведении лежат в одной плоскости, – плоскости параллелизма, т.е. они компланарны.

Для обратного утверждения справедлива теорема.

Теорема 2.1.

Достаточное условие того, что данная линейчатая поверхность является поверхностью Каталана.

Пусть задана линейчатая поверхность

,

причем вектор-функция  трижды непрерывно дифференцируема (здесь и далее мы говорим о каком-либо простом куске поверхности, которому отвечают некоторые промежутки параметров). Тогда если и  неколлинеарен  ни в одной точке то данная поверхность является поверхностью Каталана.

Доказательство.

Рассмотрим два случая: когда кривая, описываемая вектором  – плоская и когда она неплоская.

1) Предположим, что кривая  – плоская. Тогда равенство  просто следует из этого факта. Очевидно, что все тройки векторов (при любом значении параметра) лежат в плоскости кривой . Поэтому и все образующие лежат в этой плоскости, значит и поверхность является по определению поверхностью Каталана.

2) Предположим, что кривая  – неплоская. По условию теоремы . Продифференцируем это равенство один раз по параметру:

.

Если  коллинеарен вектору  в некоторой точке. Тогда

Значит  коллинеарен , а значит,  коллинеарен и , а мы предположили противное, значит, этот случай невозможен, т.е.  неколлинеарен вектору .

Посмотрим на картинку:

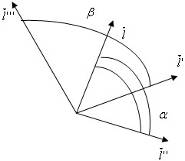
Так как , то все эти три вектора лежат в одной плоскости – плоскости . А в силу того, что , эти векторы тоже лежат в одной плоскости – плоскости  (в первом случае плоскость обозначена двумя дугами, во втором, одной дугой). Так как векторы  и  неколлинеарны, то они в обоих случаях определяют плоскость, т.е. плоскости  и  – совпадают, а значит, все четыре вектора: , , ,  лежат в одной плоскости, а значит: .

Напомним, что если дана кривая . То кручение кривой в точке  вычисляется по формуле:

                                                                            (*)

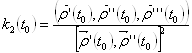Т.к.  – то кривая  – плоская, а это противоречит предположению пункта два. Т.е. рассматриваемая ситуация невозможна.

Таким образом, кривая  (в условиях теоремы) может быть только плоской кривой и при этом поверхность является поверхностью Каталана ч.т.д.

Замечание 2.3. Если в теореме убрать предположение о тройной непрерывной дифференцируемости вектор-функции . То можно построить пример поверхности, такой что , но при этом поверхность не является поверхностью Каталана.

Красивый пример можно получить следующим образом.

Нам хочется, чтобы функция  «развернула» плоскость прямых или разворачивала ее постоянно. Как следует из теоремы, соответствующую функцию следует искать среди функций, 3-яя производная которых терпит в какой-либо точке разрыв.

Например, можно задаться следующим уравнением: .

Здесь  – функция Хэвисайда.

Проинтегрируем это уравнение.

.

Теперь уже гораздо проще подобрать необходимый пример.

Итак, рассмотрим поверхность.

Проверим, что в каждой точке выполняется равенство: .

Замечание 4. Строго говоря, мы тут допустили неточность. А именно: . Т.е. производная тета-функции Хэвисайда – дельта-функция Дирака. Поэтому,

.

Однако, простое геометрическое рассуждение может убедить нас, что вторым слагаем можно пренебречь. Действительно, посмотрим на график функции:

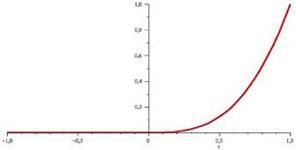
Очевидно, что в нуле наклон касательной к графику функции равен нулю, а функция  равна нулю всюду, кроме, быть может, нуля, следовательно, вклад в значение производной эта функция не вносит. Таким образом, Наше выражение для производной вполне корректно.

.

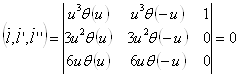Проверим условие коллинеарности векторов  и .

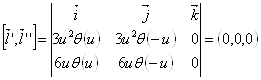
Как мы видим, они коллинеарны в каждой точке.

Теперь нам надо отыскать три прямые, которые вместе не лежат в параллельных плоскостях.

Для этого найдем три значения направляющего вектора этих прямых.

,

,

Если эти три вектора некомпланарны, то отвечающие им прямые (для которых они являются направляющими векторами) не лежат в параллельных плоскостях, т.е. являются искомыми.

.

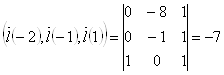Т.е. эти прямые действительно не лежат в параллельных плоскостях.

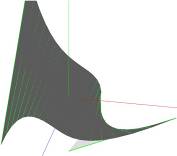
Ниже на рисунке изображен пример такой поверхности. Мы отчетливо видим, как на этой поверхности есть прямы, соответствующие данным векторам.

Более простой пример можно построить, убрав требование о том, что  неколлинеарен .

Найдем вектор, который в каждой точке обладает свойством, обратным к данному.

Пусть  коллинеарен вектору  при каждом значении параметра. Например:

Пусть .

Решим уравнение, например, для координаты .

Сделаем замену: .

.

.

Подставим в .

. Т.е.  имеет вид:

Вычислим производные для проверки.

,

.

Теперь видно, что в каждой точке векторы  и  коллинеарные, поэтому смешанное произведение будет заведомо равно нулю (другого и быть не могло, собственно).

Теперь нам надо сделать так, чтобы нашлись 3 вектора  не лежащие в одной плоскости (при соответствующих значениях параметра).

Т.е.

,

,

.

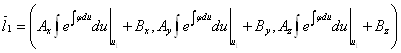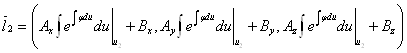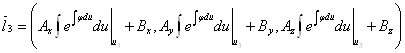И при этом: .

Поскольку сдвиг в пространстве всех этих трех векторов не повлияет на равенство (или не равенство) нулю смешанного произведения, то достаточно рассматривать векторы:

,

,

.

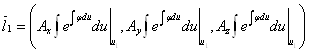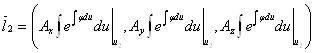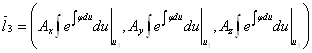А эти векторы, очевидно, лежат в одной плоскости. Так что добиться выполнения утверждения о коллинеарности векторов  и  в каждой точке, при выполнении, которого поверхность не будет являться поверхностью Каталана – нельзя.

Значит, стоит подумать о примере, который обеспечивает выполнение этого условия в одной точке, в которой, разумеется, мы должны «повернуть» плоскость образующих линейчатой поверхности.

Рассмотрим вектор:

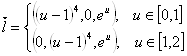
Очевидно:

,

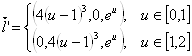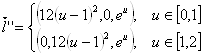
Очевидно, что  в каждой точке (есть нулевой столбец). Также, за исключением точки, соответствующей параметру  кручение вектора  также равно нулю (). Причем, в каждой точке промежутка:  неколлинеарен  (т.е. мы имеем право пользоваться формулой (*) для расчета кручения кривой на указанном промежутке).

Действительно:

Если : , .

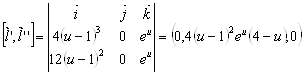
График ординаты имеет вид:

И мы видим, что он нигде кроме 1 в нуль не обращается (это видно и непосредственно из аналитического выражения).

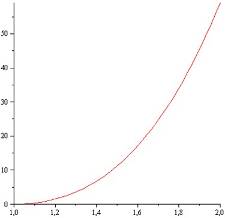
Если : , .

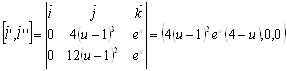
Аналогично – график на данном полуинтервале:

Теперь мы уже поняли, что  коллинеарен в точке . Следовательно, вычислять кручение кривой в этой точке по формуле (*) нельзя. Как мы сейчас увидим, в результате – кривая  не будет плоской.

Действительно, возьмем три вектора:

,

,

.

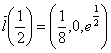Проверим, лежат ли они в одной плоскости.

.

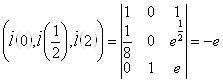Действительно, они некомпланарны, а следовательно, и соответствующие этим векторам прямые не лежат