Скачать

Динамика рыночной экономики

Динамика рыночной экономики

Традиционный подход к динамике рыночных отношений предполагает рассмотрение приспособительных реакций экономики на внешние воздействия в "кратчайшем", "краткосрочном" или "долговременном" периодах. Весь анализ основан на графических построениях и сводится к сравнению начальных и конечных равновесных состояний. Сам процесс перехода из одного состояния в другое остается без внимания (1).

Цель данной работы – разработка математических моделей, описывающих динамику поведения макроэкономических систем.

Рассмотрим экономические модели:

- чистой монополии,

- чистой конкуренции,

- монополистической конкуренции и олигополии.

Примем следующие определения и допущения:

1. Планируемый спрос – объем товаров в натуральном или денежном выражении по ценам, действующим на принятый за базовый момент времени, который потребители планировали или планируют приобрести на некоторый начальный момент времени или за любой выделенный его промежуток.

2. Потребительский спрос – спрос на товары личного потребления. Так как конечной целью любой экономики является удовлетворение личных потребностей, именно спрос на потребительские товары является первичным, определяющим размер производства. "Уровень жизни людей зависит в первую очередь от количества товаров, произведенных и направленных в руки семей и отдельных индивидов…" (2).

3. Текущий спрос – разность между планируемым спросом и тем количеством товаров в натуральном или денежном выражении по действующим на базовый момент времени ценам, которое было реализовано на внутреннем рынке к данному моменту времени.

4. Ограниченный спрос – количество товаров в натуральном или денежном выражении, потребность в котором может быть полностью удовлетворена. "Хотя, вообще говоря, потребности людей безграничны, потребность в определенном товаре может быть удовлетворена" (3).

5. Неограниченный спрос – спрос, который существует на постоянной основе и не может быть полностью исчерпан.

6. Расширяющийся спрос – спрос, прямо зависящий от количества реализованного к данному моменту времени товара.

7. Годовой спрос (годовой прирост спроса) − величина спроса в текущем году. Годовой спрос принимается численно равным абсолютному значению производной по времени на начало текущего года от функции, описывающей спрос, при измерении времени в годах. (Изменение функции с достаточной точностью может быть оценено по ее дифференциалу).

8. Производный (вторичный) спрос – спрос, обусловленный наличием потребительского спроса. Например, спрос на инвестиционные товары, ресурсы является производным от потребительского спроса. Производным является и спрос на услуги, такие, например, как управленческие услуги, медицинские услуги; услуги по гарантийному и текущему техническому обслуживанию, ремонту; услуги по реализации товаров и так далее. "Спрос на ресурсы является производным спросом, т. е. производным от готовых товаров …" (4). Будучи вторичным, производный спрос не оказывает прямого влияния на размер производства.

9. Объем производства – количество товаров в натуральном или денежном выражении по ценам, действующим на момент времени, принятый за базовый, которое произведено к данному моменту времени. Это реальный физический объем производства, выраженный в натуральной или эквивалентной денежной форме по тем же ценам, что и спрос.

10. Годовой объем производства (годовой прирост продукции) − объем товаров, произведенный в текущем году. Принимается численно равным производной по времени на начало текущего года от объема производства при измерении времени в годах. Аналог данной величины – валовой национальный продукт (ВНП).

11. Рынок – структура, обеспечивающая распределение товаров. В более широком смысле рынок – экономическая система в целом.

12. Предложение – количество потребительских товаров, поставляемых на рынок.

13. Емкость рынка – планируемый спрос на товар, текущая емкость рынка – текущий спрос на товар.

14. Ограниченный рынок – рынок с ограниченным спросом, расширяющийся рынок – рынок с расширяющимся спросом, неограниченный рынок – рынок с неограниченным спросом.

15. Статичная экономика – экономика с постоянными средним годовым планируемым спросом и средним годовым объемом производства.

16. Количество товаров, спрос, объемы производства измеряются в у. е. (условных единицах).

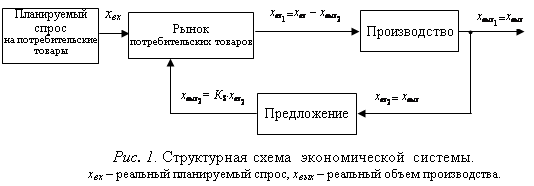
Экономическую систему, основанную на спросе и предложении, можно представить следующей структурной схемой (см. рис.1):

динамика монополия олигополия конкуренция

Ее можно рассматривать как динамический объект с отрицательной обратной связью по предложению. Входной величиной для системы является планируемый спрос, выходной – объем производства. Рынок можно рассматривать как элемент сравнения спроса и предложения, производство - как объект регулирования. Регулирующую роль в системе играет предложение. При отклонении предложения от спроса появляется стимул для изменения размера производства, а, следовательно, и величины предложения.

Аналитически динамические свойства выражаются обычно дифференциальными уравнениями, графически, наглядно, – кривыми переходных процессов, представляющих реакции объекта на типичные входные воздействия. Примером может служить временная характеристика – изменение во времени выходной величины под действием скачкообразного изменения входной. При этом виде воздействия входная величина мгновенно изменяется на конечную величину, в дальнейшем оставаясь постоянной. Часто оказывается удобным другой способ выражения динамических свойств – передаточная функция, представляющая собой динамический коэффициент передачи объекта.

Динамические характеристики системы в целом складываются из динамических характеристик структурных единиц – элементов.

Рассмотрим динамические характеристики элемента "Производство" для различных моделей экономики.

Динамика товарного производства. Чисто монопольный рынок ограниченного объема

Обозначим количество товара через "х". Примем, что единственный производитель поставляет на рынок, емкость которого х_вх = const ограничена, пригодный к неограниченно долгому использованию товар.

Если товара на рынке мало, т. е. он дефицитен, то любое количество раскупается сразу, скорость реализации велика, так как велико число покупателей. По мере насыщения рынка число покупателей сокращается, и скорость реализации падает. Наконец, если рынок насыщен товаром, скорость реализации становится равной нулю. "Чем большее количество продукта приобретают потребители, тем меньше их стремление к получению дополнительных единиц этого же продукта" (5).

Логично принять, опираясь на приведенные выше рассуждения, что скорость реализации пропорциональна текущему спросу, то есть разнице между планируемым спросом (емкостью рынка)"х_вх" и количеством реализованного к данному моменту товара"x".

Тогда скорость реализации составит

V_p=c×(x_вх – x) …………….……….….. (1),

где  "х"- количество реализованного к данному моменту времени "t" товара, у.е.,

х_вх –планируемый спрос, у. е.,

с – коэффициент пропорциональности, имеющий размерность времени.

Единственный производитель способен полностью контролировать рынок. Ему выгодно, чтобы минимизировать издержки и получить максимальный общий доход и прибыль, поддерживать постоянной цену товара, а скорость производства, равной скорости реализации, то есть "работать с колес".

Выберем произвольный момент времени "t" и рассмотрим баланс товара на рынке за бесконечно малый промежуток времени "dt ". За этот промежуток времени будет произведено количество товара, равное "dx", а реализовано количество товара, равное"c×(x_вх – x)∙dt". Из условия, что произведенный товар будет немедленно реализован, следует, что эти количества должны быть равны:

dx = c×(x_вх – x)∙dt …………………..... (1.1).

Разделив обе части на "dt", получим:

dx/dt = c×(x_вх – x) …………………..... (1.2).

Тот же результат можно получить, если приравнять скорости производства и реализации товара.

Скорость производства товара равна приращению массы товара на рынке в единицу времени, т. е.

V_п= dx/dt…………………..…….… (1.3),

Приравнивая (1) и (1.3), получим дифференциальное уравнение, описывающее динамику производства:

dx/dt = c×(x_вх – x)……………..(1.2),

 …………..…. (1.4),

……………….(1.5).

Решением уравнения (1.5) при нулевых начальных условиях (x= 0 при t= 0) и х_вх = соnst (х_вх = 0 при t<0, х_вх ≠0 при t≥0) будет:

 ………..… (1.6),

где х – объем производства − выходная величина объекта, у.е.,

х_вх – планируемый спрос − входная величина для объекта, у.е.,

T₁ =1/c – постоянная времени объекта.

Чисто монопольный, расширяющийся рынок

Реальный товар имеет ограниченный срок использования, например, вследствие морального или физического износа, т. е. безвозвратно расходуется в процессе потребления. Для замены использованного товара требуется производить дополнительное количество нового товара, причем это дополнительное количество пропорционально уже выпущенному количеству, т. е. по мере роста выпуска происходит расширение планируемого спроса "х_вх" на величину "l×х", где "х" - масса уже выпущенного товара, а l<1 – коэффициент расширения спроса. Спрос "х_вх" может быть функцией времени.

Итак, текущий спрос составит

((x_вх + l×х) – x)) …………………...… (2),

скорость реализации

V_p=c×((x_вх + l×х) – x)) ……………... (2.1),

скорость производства

V_п= dx/dt ……….……………….…(2.2).

Приравнивая (2.1) и (2.2), получим следующее дифференциальное уравнение:

dx/dt = c×((x_вх + l×х) – x))  ………… (2.3)

или

 ……………….…(2.4),

где Т₁ =  - постоянная времени: параметр, характеризующий динамику производства в условиях чистой монополии,

К =  - структурный мультипликатор спроса (или статический коэффициент передачи объекта).

Структурным мультипликатор назван потому, что он относится к конкретной структурной единице – производственному сектору и характеризует его производственные возможности.

Можно принять , исходя из того, что λ = 0, когда срок службы товара"t_с" не ограничен (t_с =¥), и "λ" стремиться к 1 (λ<1), когда срок службы товара приближается к времени его реализации "t_р". Здесь "D" − некоторая константа.

Структурный мультипликатор − аналог мультипликатора дохода, обычно определяемого как "отношение изменения ЧНП к соответствующему изменению первоначальных расходов" (6), а коэффициент расширения спроса "λ" не что иное, как аналог "предельной склонности к потреблению"⁽⁷⁾ .

Решение уравнения (2.4) при нулевых начальных условиях (x_t=0 = 0) и при х_вх = const будет иметь вид:

 ………………(2.5).

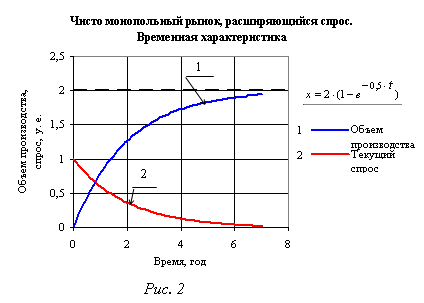
На рис. 2 приведена временная характеристика модели с постоянной времени Т₁ = 2 года (с =1 год⁻¹; l= 0,5) и коэффициентом передачи К = 2, представляющая собой зависимость объема производства от времени при входном скачкообразном воздействии (изменении спроса) х_вх = 1 у.е.. По временной характеристике можно судить о динамических свойствах объекта. В данном случае по принятой классификации объект– апериодическое звено первого порядка (8).

Чисто конкурентный, расширяющийся рынок

Для чистой конкуренции характерно следующее (9):

- отраслевое производство увеличивается или сокращается только за счет изменения числа предприятий, причем отрасль может расширяться или сужаться без существенного влияния на цены и затраты ресурсов;

- отдельный производитель не в состоянии повлиять ни на цену товара, ни на общий объем производства;

- производители могут, как легко входить в рынок, так и легко покидать его;

- увеличение спроса не влияет на уровень цен, так как отраслевое предложение представляет собой горизонтальную линию.

Естественно поставить скорость образования новых предприятий в зависимость от спроса. В начальный момент, когда число предприятий незначительно, а спрос велик, скорость образования новых предприятий будет велика. При текущем спросе, равном нулю, новые предприятия возникать не будут.

Допустим, что скорость образования новых предприятий пропорциональна текущему спросу, т. е.

 ………….…...(3),

где "N" – число предприятий.

В условиях чистой конкуренции экономические показатели отдельных предприятий неизбежно выравниваются, то есть

v₁ = v₂=… v_j = …=v_N = c₂ ………...(3.1),

где "v_j" - скорость производства отдельного предприятия (типичной фирмы).

Суммарная скорость производства (отраслевая скорость) пропорциональна числу производителей:

…………….….…(3.2),

Откуда

……………...……..(3.3).

Подставив (3.3) в (3) и произведя преобразования, получим (с=с₁∙с₂):

 ……….... (3.4)

или

 ……………… (3.5),

где х_вх – планируемый спрос (входная величина),

 - параметр, характеризующий динамику производства в условиях чистой конкуренции,

К =  - структурный мультипликатор спроса.

Решением уравнения (3.5) при нулевых начальных условиях

(t= 0,  x_t=0 = 0, ) и при x_вх= const

является выражение:

 …..……...(3.6),

где 

 …………….…..……(3.7).

Здесь w₁ - круговая частота цикла, А₁ – амплитуда цикла. Период цикла связан с круговой частотой соотношением

 ………………….(3.8).

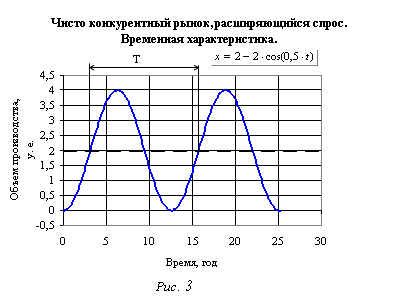
На рис. 3 показана реакция модели с параметрами Т₂ =2 года (с = 0,5 год⁻²; l= 0,5) и К = 2 на входное воздействие (скачкообразное изменение спроса)  х_вх = 1 у. е., а именно: зависимость объема производства от времени.

Данная структурная модель представляет собой чисто колебательное звено.

Расширяющийся рынок с монопольной конкуренцией

Уравнение процесса для данного случая можно получить, поставив в соответствие реальному рынку составной рынок, состоящий из двух частей: чисто конкурентной и чисто монопольной, суммарный объем производства и суммарный спрос которых равны соответственно объему производства и спросу на реальном рынке. Такое рассмотрение позволяет ввести непрерывную величину − показатель конкуренции "k", как долю объема производства и спроса, приходящуюся на конкурентную часть составного рынка, и связать ее с числом производителей на рынке. Каждую часть рынка можно, воспользовавшись выведенными выше уравнениями для чистой монополии и чистой конкуренции, описать собственным уравнением, исходя из доли приходящегося на нее объема производства и спроса.

Объем производства конкурентной части рынка и приходящийся на нее спрос составят соответственно"k×x" и "k×x_вх", где k –показатель конкуренции (0<k<1), "х" – текущий объем производства реального рынка, "х_вх" - спрос на реальном рынке. Тогда чисто конкурентную часть рынка можно описать уравнением:

 ….............(4).

Чисто монопольная часть рынка в свою очередь будет описываться уравнением:

 …...(4.1).

При суммировании этих двух уравнений получим рынок с объемом производства и спроса, равным таким же величинам реального рынка, и уравнение, описывающее расширяющийся рынок с монопольной конкуренцией:

 … (4.2),

 …….……... (4.3),

где

 и  − параметры динамики модели.

Решение уравнения (4.3) при Т₃ < 2∙Т₄ с учетом начальных условийt = 0,  x = 0,  и при входном воздействии х_вх = соnst и можно записать в виде:

……...… (4.4),

где

.…(4.5),

…………..………(4.6).

Здесь σ – коэффициент затухания цикла, ω₂ – круговая частота цикла, β – фаза цикла, А₂ – амплитуда цикла.

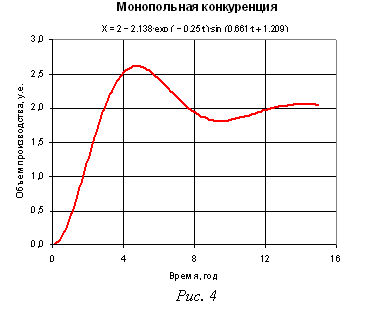
На рис. 4 показана временная характеристика, то есть зависимость объема производства от времени, для модели с параметрами Т₂ =2 года, Т₁ = 2 года, К = 2, k = 0,5 при входном воздействии (скачкообразном изменении спроса) х_вх = 1 у. е. Такая временная характеристика характерна для колебательного звена с затуханием.

Уравнение (4.2) можно считать обобщенной динамической характеристикой элемента "Производство" для всех моделей экономики. Все рассмотренные случаи могут быть получены из него при значениях коэффициента конкуренции "k" в диапазоне от нуля до единицы.

Записанное в операторной форме уравнение (4.2) будет иметь вид:

…………..(4.7),

а передаточная функция элемента (сектора) "Производство" может быть представлена следующим выражением (10):

 .….…(4.8),

где  х_вх – значение сигнала на входе элемента (хвх₁ на рис.1),

х – значение сигнала на выходе элемента (хвых₁ на рис.1),

Т₂ – параметр, характеризующий динамику элемента при чистой конкуренции (динамику конкурентной части);

Т₁ − параметр, характеризующий динамику элемента при чистой монополии (динамику монопольной части);

р - оператор дифференцирования.

Статической характеристикой элемента является линейная зависимость:

х = К∙х_вх ……………………….. (5).

Статическая характеристика – зависимость выходной величины от входной в равновесных состояниях объекта. Состояние объекта, при котором возмущения отсутствуют, а входная и выходная величины сохраняют постоянные значения, называется равновесным. Статическая характеристика позволяет определить величину выходного сигнала в зависимости от заданной величины входного при переходе объекта из одного равновесного состояния в другое (11).

Если объект, будучи выведен из состояния равновесия действием возмущения, после устранения последнего стремится снова вернуться в состояние равновесия, то он является устойчивым. Если же выходная величина с течением времени все дальше удаляется от заданного значения или непрерывно колеблется вокруг него – объект неустойчив (12).

Известно, что уровень конкуренции есть функция числа производителей k = f(N) (13), где "N", очевидно, равно числу производителей, когда система находится в состоянии равновесия. Эту зависимость, учитывая, что для чистой конкуренции k = 1, а для чистой монополии k = 0, можно аппроксимировать выражением:

……………………..(5.1).

При большом "N" (N→∞), что отвечает случаю чистой конкуренции, показатель конкуренции "k", вычисленный по предложенной зависимости (5.1), практически не отличается от единицы, а при N = 1, что отвечает случаю чистой монополии, равен нулю. На практике "N" можно принимать равным среднему числу производителей за достаточно большой промежуток времени или среднему числу за экономический цикл.

Обратная зависимость будет иметь вид:

  ………...……..(5.2).

Динамика экономической системы

Примем, что запаздывания (временные лаги) в экономической системе (см. рис.1), связанные с принятием решений об увеличении или сокращении объемов производства, с подготовкой производства при изменении спроса, с задержками на линии реализации продукции, отсутствуют или незначительны, и что передаточную функцию структурного элемента «Предложение» можно представить в виде:

W₂() =  = К_S….………….....… (6),

где К_S –коэффициент передачи цепи обратной связи (К_S ≤1).

Тогда передаточная функция системы в целом будет иметь вид (14):

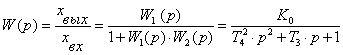  …. (6.1),

причем

…………….......(6.2),

…….…....(6.3),

и, следовательно, система в целом будет описываться следующим дифференциальным уравнением:

 ..….... (6.4),

где К₀ – системный мультипликатор спроса (статический коэффициент передачи системы),

Т₃ – имеющий размерность времени параметр, характеризующий динамику системы при чистой конкуренции (динамику конкурентной части),

Т₄ − имеющий размерность времени параметр, характеризующий динамику системы при чистой монополии (динамику монопольной части),

х_вх– размер планируемого спроса,

х_вых– размер производства.

Приравнивая знаменатель передаточной функции (6.1) нулю, получим характеристическое уравнение системы:

= 0…………..……….. (6.5).

Если корни этого уравнения  комплексные (Т₃<2∙Т₄), решением дифференциального уравнения (6.4) будет колебательный процесс.

Обозначим:

…... (6.6).

Тогда , где s - коэффициент затухания, w₂ - круговая частота цикла.

Полагая Т₁/(2×Т₂²) = а = соnst (Т₁ и Т₂ по определению не зависят от "k"), получим уравнение, связывающее коэффициент затухания с показателем конкурентности рынка:

 ….……….………… (6.7).

Здесь коэффициент "а" можно рассматривать как параметр цикличности, так как от него зависит скорость затухания колебаний.

Современное производство включает два сектора: потребительский и средств производства. Для обеспечения выпуска потребительских товаров, общество вынуждено производить соответствующее количество орудий труда. С экономической точки зрения коэффициент передачи цепи обратной связи "К_S" представляет собой коэффициент распределения дохода между этими двумя секторами. "То, что затрачено потребителем на приобретение продукта, получено в виде дохода теми, кто участвовал в его производстве" (15).

Рассмотрим реакцию моделей на скачкообразное изменение спроса. Напомним, что реакция на скачкообразное изменение входного сигнала − одна из характеристик, по которой можно наглядно судить о динамических свойствах системы.

Для случая чистой конкуренции (k = 1) будем иметь:

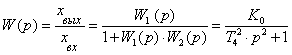..………………....…(7),

…..….(7.1),

  ………………………...(7.2).

При нулевых начальных условиях  (xвых_t=0 = 0,  dxвых/dt_t=0,= 0),  полагая  xвх = const (x_вх = 0 при  t<0,x_вх  ≠ 0 при t³ 0), получим следующее решение уравнения (7.2):

…………......….…….(7.3),

где 

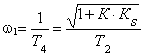 − круговая частота цикла…………..…… (7.4),

 − амплитуда цикла………………... (7.5).

Период цикла связан с круговой частотой соотношением

 …………………………….…..(7.6).

Из (7.3) следует, что в случае чистой конкуренции временная характеристика системы представляет собой незатухающие гармонические колебания (циклы) около средней линии−состояния равновесия х_вых=К₀×х_вх(16), причем с увеличением структурного мультипликатора частота колебаний растет. Амплитуда цикла пропорциональна интенсивности возмущения. Эти незатухающие колебания объема совокупного продукта – присущая системе естественная цикличность. "Термин экономический цикл означает следующие один за другим подъемы и спады уровней экономической активности. Отдельные экономические циклы существенно отличаются друг от друга по продолжительности и интенсивности (17)". Последнее, вероятно, объясняется возникновением биений при наложении многочисленных в реальных условиях внешних возмущений на естественную цикличность. Следует отметить, что в состоянии равновесия колебания отсутствуют. В то же время любое внешнее воздействие приводит к появлению незатухающих колебаний. Такая система не считается устойчивой (18). Напомним, что устойчивой считается система, стремящаяся после устранения возмущения вернуться в состояние равновесия. "Неустойчивость рыночной экономики, сказывающаяся на объеме совокупного продукта, занятости и уровне цен, представляет собой вечную проблему" (19).

Для полностью монополизированной экономики (k = 0) при начальных условиях t = 0, xвых_t=0 = 0 и при  xвх = const имеем:

…(7.7),

……………….….…….……....(7.8),

 ………………..………...(7.9).

Полностью монополизированная экономика устойчива, собственная (внутренняя) цикличность отсутствует, скорость выравнивания при возмущениях растет с увеличением структурного мультипликатора: ускоряется переходной процесс. В равновесных состояниях . Временная характеристика представляет собой экспоненциальную зависимость (7.9) (20).

Для случая монополистической конкуренции (0

При начальных условиях t = 0, xвых_t=0 = 0, dx_вых/dt_{t = 0} и xвх = const решение уравнения (6.4) можно записать в виде:

……………..……….… (7.10),

где  − частота цикла,  – амплитуда цикла,  – фаза цикла,  – коэффициент затухания.

В равновесных состояниях .

Модель устойчива: временная характеристика – затухающие гармонические колебания (7.10) (21). При увеличении степени монополизации время стабилизации системы при действии возмущений и цикличность, если под этим подразумевать число циклов до возвращения системы в состояние равновесия, уменьшаются.

Удобнее другая форма уравнений (6.4), (7.2), (7.8), полученная их дифференцированием:

для монополистической конкуренции

 ….(8),

для чистой конкуренции

 ..………….(8.1),

для чистой монополии

 ………………(8.2).

Здесь в качестве переменных фигурируют годовые показатели: Y_вх – годовой планируемый спрос, Y_вых – годовой объем производства.

Системный мультипликатор "К₀ "отражает фундаментальную для экономики связь между планируемым спросом и размером производства.

Для равновесных состояний всех моделей имеем х_вых =К₀∙х_вх, в том числе для годовых значений объема производства и планируемого спроса – Y_вых=К₀∙Y_вх. Эти соотношения верны и для средних значений соответствующих величин. В частности, средними являются значения, полученные исключением из решений циклической составляющей.

Учитывая, что при равновесии

,

получим:

Y_{вх ср} = (1 – λ)∙Y_{вых ср} + К_S∙Y_{вых ср} …….….…..(9),

где Y_{вх ср} – равновесный (или средний) годовой планируемый спрос,

Y_{вых ср} – равновесный (или средний) годовой объем производства.

Первый член YАср = (1– λ)∙Y_{вых ср} выражения (9) может быть отождествлен со средними годовыми затратами, необходимыми для полного восстановления израсходованных средств производства (амортизация), второй Y_Pср = К_S∙Y_{вых ср} – со средними годовыми поставками потребительских товаров на рынок (предложением).

В то же время

Y_{вых ср}= К_S∙Y_{вых ср} + (1 − К_S)∙Y_{вых ср} ……....(9.1).

Здесь выражение YВср = (1 − К_S)∙Y_{вых ср} представляет собой фактические годовые затраты на инвестиционные товары, т. е. валовые инвестиции.

Для статичной экономики годовой текущий спрос Y_ср = Y_{вх ср} – (1 – λ)∙Y_{вых ср} равен годовым поставкам на рынок Y_Рср = К_S∙Y_{вых ср}, так как из (9) следует

Y_{вх ср} – (1 – λ)∙Y_{вых ср}= К_S∙Y_{вых ср}….…….…(9.2),

Чтобы иметь возможность применять полученные уравнения к открытой экономике, введем в рассмотрение коэффициенты (доли) соответственно К_M импорта и К_X экспорта как части собственного выпуска продукции, т. е.

К_M = Y_M/Y_вых,К_X = Y_X/Y_вых ….……(10),

где Y_M – величина импорта, Y_Х – величина экспорта.

Коэффициент распределения дохода для этого случая определим следующим образом:

К_S,о = К_S + К_M – К_X ……….…… (10.1),

где К_S –коэффициент распределения без учета импорта и экспорта.

Системный мультипликатор спроса для открытой экономики будет равен:

…..(10.2),

собственные годовые поставки на рынок составят

Y_Р = К_S,о∙Y_вых …………….…(10.3),

валовые инвестиции

Y_В = (1– К_S,о)∙Y_вых ………....(10.4),

амортизация, т. е. затраты на полное восстановление израсходованных средств производства,

Y_А = (1– λ)∙Y_вых …………….(10.5),

чистые инвестиции

I = (Y_В − Y_А) = (λ –К_S,о)∙Y_вых ….….(10.6).

Собственный годовой выпуск продукции составит:

…………………..….(10.7).

Эти соотношения будут действительны и для закрытой экономики при условии замены К_S,о на К_S.

Введем в рассмотрение еще один экономический показатель−общее потребление, и определим его следующим образом:

Q = Y_Р + Y_В + Y_M − Y_Х = (1+К_M −К_X)∙Y_вых ….. (10.8).

Целесообразность введения этого показателя станет ясной из дальнейшего изложения.

Покажем, что существует связь между системным мультипликатором спроса и чистыми инвестициями как долей дохода. Выражение для системного мультипликатора можно переписать следующим образом:

……….. (10.9),

где d_А = (1 − λ) − норма амортизации, d_В = (1 − K_S) – доля валовых инвестиций, d_I = (d_В − d_А) − доля чистых инвестиций.

Будем считать сбалансированной экономику, в которой средний годовой планируемый спрос Y_{вх ср} в точности равен среднему годовому производству продукцииY_{вых ср}, то есть расходы равны доходам. Сбалансированная экономика – это экономика полной занятости и полного объема производства (22).

В несбалансированной экономике разница между спросом Y_{вх ср} и выпускомY_{вых ср}  приводит к инфляции (23).

Если принять, что рост цен пропорционален относительной разности между средним планируемым спросом  и средним выпуском, то для скорости роста цен можно предложить следующее уравнение:

…………….(11),

где Р – индекс цен,

– средний (или равновесный) планируемый годовой спрос,

– средний (или равновесный) годовой выпуск,

– начальное значение среднего (или равновесного) планируемого годового спроса (индекс начального значения принимается равным 100),

t − время, год,

Ср – масштабный фактор, характеризующий скорость изменения цен, (%/год). Значения "Ср" определяются темпами изменения денежной массы и номинального дохода (24). В общем случае "С_р" может быть функцией времени.

В статичной экономике отношение

 = const.

При равномерном росте денежной массы (ежегодном увеличении на постоянную величину)

Ср = соnst, .

Подставляя эти значения в (11) и интегрируя при условии Р =100 при t = 0 (индекс начального значения = 100), получим для статичной экономики:

………….………........…(11.1).

Полагая Ср = с_р∙(1+р₁)^t/τ = с_р∙ехр (m∙t), что соответствует постоянному годовому (τ =1год) темпу "р₁" роста денежной массы, получим при условии Р_t=0=100

…….………….....(11.2),

гдеm =(ln(1+р₁)/τ),

.

Следует отметить, что при С_р = 0, то есть тогда, когда уровень цен неизменен, индекс цен – постоянная величина (Р = соnst), инфляционные процессы отсутствуют. То же всегда имеет место, когда экономика сбалансирована (годовые спрос Y_{вх ср} и выпуск продукции Y_{вых ср} равны).

Темп инфляции, то есть рост цен по отношению к предыдущему году, составит:

%  %….(11.3),

где Р(t) (или Р(t+1)) – индекс цен в текущем году,

Р(t–1) (или Р(t)) – индекс цен в предыдущем году.

Общепризнано, что отставание производства от потенциально возможного уровня при полной занятости вызывается наличием безработицы (25).

Если согласиться с тем, что безработица обусловлена отклонением производства от уровня при полной занятости, для определения уровня безработицы можно предложить следующее выражение: