Действительные числа. Иррациональные и тригонометрический уравнения

Веще́ственное, или действи́тельное число - математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений ⁽²⁾. Если натуральные числа возникли в процессе счета, рациональные - из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.

Абсолютная погрешность и её граница.

Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено $\mathsf{(a)}$ , считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой) $\mathsf{(\vartriangle a)}$ понимают разность между точным и приближенным значением числовой величины: $\mathsf{a^{*}-a=\vartriangle a}$ . Погрешность может принимать как положительное так и отрицательное значение. Величина $\mathsf{(a^{*})}$ называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность. Абсолютной погрешностью приближенного значения $\mathsf{(a^{*})}$ называют величину $\mathsf{\vartriangle (a^{*})}$ , про которую известно, что: $\mathsf{\mid a^{*}-a \mid\le \vartriangle(a^{*}).}$ Относительная погрешность и её граница.

Качество приближения существенным образом зависит от принятых единиц измерения и масштабов величин, поэтому целесообразно соотнести погрешность величины и ее значение, для чего вводится понятие относительной погрешности. Относительной погрешностью приближенного значения называют величину $\mathsf{\delta (a^{*})}$ , про которую известно, что: $\mathsf{\left| {a^{*}-a \over a^{*}} \right|= {\vartriangle (a^{*}) \over \left| {a} \right|} = \delta (a^{*})}$ . Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения.

Иррациональные уравнения

Уравнение, в которых под знаком корня содержится переменная, называют иррациональными. При решении иррациональных уравнений полученные решения требуют проверки, потому, например, что неверное равенство при возведении в квадрат может дать верное равенство. В самом деле, неверное равенство при возведении в квадрат даёт верное равенство 1²= (-1) ², 1=1. Иногда удобнее решать иррациональные уравнения, используя равносильные переходы.

Возведём обе части этого уравнения в квадрат; После преобразований приходим к квадратному уравнению; и подставим.

Комплексные числа. Действия над комплексными числами.

Ко́мпле́ксныечи́сла - расширение множества вещественных чисел, обычно обозначается $\mathbb{C}$ . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y - вещественные числа, i - мнимая единица Комплексные числа образуют алгебраически замкнутое поле - это означает, что многочлен степени с комплексными коэффициентами имеет ровно комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках - электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.

Сравнение a + bi = c + di означает, что a = c и = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Сложение (a + bi) + (c + di) = (a + c) + ( + d) i.

Вычитание (a + bi) − (c + di) = (a − c) + ( − d) i.

Умножение

$(a+bi)\cdot(c+di)=ac+bci+adi+bdi^2=(ac-bd)+(bc+ad)i.$

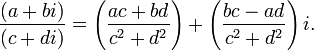
Деление $\frac{(a+bi)}{(c+di)}=\left(\frac{ac+bd}{c^2+d^2}\right)+\left(\frac{bc-ad}{c^2+d^2}\right)i.$

Числовая функция. Способы задания функции

В математике числовая функция - это функция, области определения и значений которой являются подмножествами числовых множеств - как правило, множества действительных чисел $\R$ или множества комплексных чисел $\mathbb{C}$ .

Словесный: С помощью естественного языка Игрек равно целая часть от икс. Аналитический: С помощью аналитической формулы f (x) = x!

Графический С помощью графика Фрагмент графика функции $y=\operatorname{arctg}x$ .

Табличный: С помощью таблицы значений

x	0	1	2	3	4	5	6	7	8	9
y	1	1	2	3	5	8	13	21	34	55

Подобное:

Динамика развития некоторых понятий и теорем теории вероятностей
1. Динамика развития понятия вероятности1.1 Первые попытки введения понятия вероятности1.2 Появление классического определения понятия
Диофантовые уравнения
Я выбрала тему: «Диофантовы уравнения» потому, что меня заинтересовало, как зарождалась арифметика. Диофант Александрийский (3 век)-греч
Дискретная математика
Министерство образования и наукиРоссийской ФедерацииРоссийский химико-технологический университетим. Д.И. МенделееваНовомосковский
Дифференциальная геометрия торсов в пространстве 1R4 с псевдоевклидовой касательной плоскостью
В работе исследуется геометрия поверхностей четырехмерного псевдоевклидова пространства индекса один, т.е. пространства Минковского.И
Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков
Доказательство Великой теоремы Фермас помощью метода бесконечных (неопределенных) спусков§1. Решение задач в науке определяется верифи
Дроби
СодержаниеВведение. 3Глава 1. Теоретико-методологические основы формирования математического понятия дроби на уроках математики. 61.1. Пр
Евклид и Архимед
РефератПо дисциплине: «Концепция современного естествознания»Тема: «Евклид и Архимед»ЕвклидО жизни Евклида известно очень мало. Предп

Действительные числа. Иррациональные и тригонометрический уравнения

Иррациональные уравнения

Числовая функция. Способы задания функции

Категории:

Подобное: