Двоично-ортогональные системы базисных функций
Широкое использование спектрально-частотного представления процессов при исследовании сигналов и систем (преобразование Фурье) связанно с тем, что при гармонических воздействиях колебания сохраняют свою форму при прохождении через линейные цепи (системы) и отличаются от входных только амплитудой и фазой. Это свойство используют ряд методов исследования систем (например, частотные методы).
Но при реализации алгоритмов, использующих преобразование Фурье на ЭВМ, необходимо выполнять большое количество операций умножения (миллионы и миллиарды), что занимает большое количество машинного времени.
В связи с развитием средств вычислительной техники и применения их для обработки сигналов широко используются преобразования, содержащие в качестве ортогонального базиса кусочно-постоянные, знакопеременные функции. Эти функции легко реализуются с помощью средств вычислительной техники (аппаратно или программно) и их использование позволяет свести к минимуму время машинной обработки (за счет исключения операции умножения).
К числу таких преобразований можно отнести преобразования Уолша и Хаара, которые широко используются в области управления и связи. В области компьютерной технике эти преобразования используются при анализе и синтезе устройств логического типа, комбинационных схем особенно использующих большие и сверхбольшие интегральные схемы (БИС и СБИС), содержащие сотни тысяч элементов, выполняющих различные логические функции. Преобразования Уолша и Хаара используют кусочно-постоянные функции Уолша, Радемахера, и др., принимающие значения ±1, либо Хаара, принимающие значения ±1 и 0 на интервале определения (-0,5, 0,5) либо (0, 1).
Все эти системы взаимосвязаны и каждую из них можно получить как линейную комбинацию из другой (например: система Радемахера- составная часть системы Уолша). Обозначение функций связанных с авторами этих функций:
Уолша - Walsh - wal(n, Q),
Хаара- Haar- har(l, n ,Q),
Радемахера - Rademacher - rad(m, Q),
Адамара - Hadamard - had(h, Q),
Пели - Paley - pal(p, Q).
Все эти системы функции представляют собой системы двоично–ортогональных базисных функций.
1. Функции Радемахера
Функции Радемахера можно определить по формуле :
rad(m,Q) = sign(sin(2mQ)), (1)
где 0 £ Q < 1- интервал определения; m- номер функции; m = 0, 1, 2, ...
Для m = 0 функция Радемахера rad(0,Q) = 1.
Знаковая функция sign(x) определяется соотношением
 (2)
(2)
Функции Радемахера это периодические функции с периодом 1, т. е.
rad(m,Q) = rad(m,Q+1).
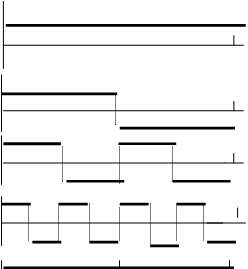
Первые четыре функции Радемахера показаны на рис. 1.
1
0 rad(0, Q)
-1
1
0 rad(1, Q)
-1
1
0 rad(2, Q)
-1
1 rad(3, Q)
0
-1
Q
0 0.51
Рис. 1. Функции Радемахера
Дискретные функции Радемахера определяются дискретными значениями Q в точках отсчета. Например: Rad(2,Q) = 1, 1, -1, -1, 1, 1, -1, -1.
Функции Радемахера ортогональные, ортонормированные (3) но являются нечетными, а значит, не образуют полную систему функций, т. к. существуют и другие функции ортогональные функциям Радемахера (например: rad(m,Q) = sign(cos(2mQ))) поэтому их применение ограничено.
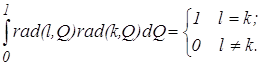 (3)
(3)
Полными двоично-ортогональными системами базисных функций являются системы функций Уолша и Хаара.
2. Функции Уолша
Функции Уолша представляют собой полную систему ортогональных, ортонормированных функций. Обозначение: wal(n, Q), где - номер функции, при этом: n = 0, 1,... N-1; N = 2i ; i = 1, 2,….
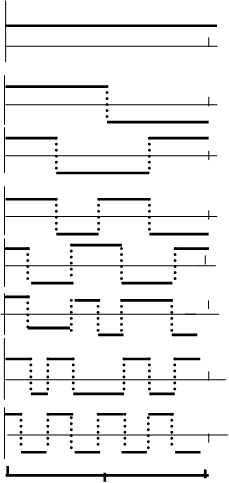
Первые 8 функций Уолша приведены на рис. 2.
 1
1
0 wal(0, Q)
-1
1
0 wal(1, Q)
-1
1
0 wal(2, Q)
-1
1
0 wal(3, Q)
-1
1
0 wal(4, Q)
-1
1 wal(5,Q)
0
-1
1wal(6,Q)
0
-1
1 wal(7,Q)
0
-1
Q
0 0.5 1
Рис. 2. Функции Уолша
Функция Уолша имеет ранг и порядок. Ранг –число единиц в двоичном представлении n. Порядок - максимальный из содержащих единицу номер разряда двоичного представления. Например, функция wal(5,Q) имеет ранг- 2 а порядок –3 (n = 5Þ 101).
Функции Уолша обладают свойством мультипликативности. Это значит, что произведение любых двух функций Уолша также является функцией Уолша: wal(k,Q)wal(l,Q)= wal(p,Q), где p = k Å l. В связи с возможностью применения к функциям Уолша логических операций, они широко используются в многоканальной связи с разделением по форме (используется также временное, частотное, фазовое и т. д. разделение), а также аппаратуре формирования и преобразования сигналов на базе микропроцессорной техники.
Функции Уолша можно получить как произведение функций Радема-хера, номер которых соответствует коду Грея номера функции Уолша. Соответствия для первых 8 функций Уолша приведены в табл. 1.
Таблица 1
| N | Двоичный код n | Код Грея | Соотношения |
| 0 | 000 | 000 | wal(0,Q)=1 |
| 1 | 001 | 001 | wal(1,Q)=rad(1,Q) |
| 2 | 010 | 011 | wal(2,Q)=rad(1,Q)×rad(2,Q) |
| 3 | 011 | 010 | wal(3,Q)=rad(2,Q) |
| 4 | 100 | 110 | wal(4,Q)=rad(2,Q)×rad(3,Q) |
| 5 | 101 | 111 | wal(5,Q)=rad(1,Q)×rad(2,Q)×rad(3,Q) |
| 6 | 110 | 101 | wal(6,Q)=rad(1,Q)×rad(3,Q) |
| 7 | 111 | 100 | wal(7,Q)=rad(3,Q) |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Двухзеркальная параболическая антенна круговой поляризации по схеме Кассегрена
- Двухканальная осциллографическая приставка к ПК
- Действие электрического тока на организм человека. Оказание первой помощи. Личная гигиена монтажника
Действие электрического тока на организм человека. Оказание первой помощи. Личная гигиена.Действие электрического тока на организм чел
- Державна метрологічна система
- Дескрипторы систем АПЧ. Особенности построения и работы систем АПЧ импульсных приемников.
- Дефокусировка. Сферическая аберрация 3 порядка. Кома и неизопланатизм
- Деятельность предприятия НП РУП Экран
Copyright © https://referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

