Скачать

Влияние ресурсозависимости на экономическое развитие (на примере России)

РЕСУРСОЗАВИСИМОСТЬ И ЭКОНОМИЧЕСКОЕ РАЗВИТИЕ: НА ПРИМЕРЕ РОССИИ

1. Введение

Как известно, экспорт природных ресурсов превышает в России 10% ВВП, что обеспечивает значительное положительное сальдо текущего счета. Отношение к этому факту в российском обществе двойственное. С одной стороны, налицо чувство вины перед будущими поколениями за растрачиваемые невоспроизводимые ресурсы, с другой стороны, для ныне действующего поколения богатство природных ресурсов представляется существенным конкурентным преимуществом, отказываться от которого ему представляется нерациональным. Много внимания уделяется монетарной стерилизации, которая кажется необходимой в связи с ростом номинального чистого экспорта Но даже в профессиональной среде российских экономистов практически не обсуждается вопрос о том, что и для текущего поколения богатство природных ресурсов может оказаться отнюдь не преимуществом, а фактором, замедляющим экономическое развитие. Недостаточное внимание, уделяемое в России проблеме влияния ресурсозависимости на экономическое развитие тем более удивительно, что оно резко контрастирует с резко возросшим интересом к этой проблеме в мире.

Еще в 1950-х годах, в период становления экономики развития как научной дисциплины (например, Prebisch, 1950, Hirschman, 1958), появилась казавшаяся парадоксальной гипотеза о том, что богатство природных ресурсов замедляет развитие. Эта гипотеза, известная сейчас как «проклятие природных ресурсов» (resource curse) стала предметом особого внимания экономистов после публикаций Сакса и Варнера (Sachs, Warner, 1995, 1997, 2001), в которых эконометрически, при наличии значительного числа контролирующих переменных, установлена отрицательная статистическая зависимость между богатством природных ресурсов(1) и темпом экономического роста. Дальнейшее эмпирическое исследование проблемы «проклятия природных ресурсов» проводилось в работах Leite, Weidmann, 1999, Isham et al., 2003, Sala-i-Martin, Subramanian, 2003, Mehlum et al., 2005.

Помимо эконометрического анализа, который проводится по сравнительно большим выборкам стран, в литературе можно найти много конкретных примеров замедленного развития ресурсозависимых стран. Например, в странах ОПЕК, в среднем, ВНП на душу населения в период 1965-1988 гг. убывал на 1,3% в год, тогда как в среднем по всем странам с низким и средним доходам – возрастал на 2,2% (Gylfason, 2001). Среди стран ОПЕК впечатляющим примером является Нигерия, где в период 1965-2000 гг. нефтяные доходы на душу населения увеличились с 33 долларов до 245 долларов (в сопоставимых ценах), тогда как ВВП на душу населения остался на прежнем уровне 325 долларов (в тех же ценах). При этом в 1970-2000 гг. доля бедных в населении Нигерии (по критерию лушевого дохода меньше 1 долл. в день) возросла с 36 до 70%. (Sala-i-Martin, Subramanian, 2003). В то же время имеется немало примеров стран, наделенных природными ресурсами, но избежавших или избавившихся от ресурсозависимости и сравнительно успешно развивающихся (среди них столь разные страны как США и Ботсвана – см. Wright, Czelusta, 2004, Gylfason, Zoega. 2002).

Теоретическое объяснение «проклятия природных ресурсов» связано с анализом различных экономических и институциональных аспектов «голландской болезни» - реструктуризации экономики, которая происходит в результате получения страной дополнительных средств. «Голландская болезнь» – более широкое понятие, чем «проклятие природных ресурсов», поскольку источником полученных страной средств может быть не только увеличение добычи или изменение конъюнктуры рынка природных ресурсов, но и иностранные кредиты или иностранная помощь(2). «Голландской болезни» посвящены многочисленные исследования (см., например, Corden, Neary, 1982, Bruno, Sachs, 1982, Enders, Herberg, 1983, Corden, 1984, van Wijnbergen, 1984, Krugman, 1987, Matsuyama, 1992, Torvik, 2001).

Большинство авторов видит суть «голландской болезни» в сокращении сектора торгуемых обработанных промышленных товаров, создающего положительные экстерналии для всей экономики, тогда как другие подчеркивают роль поиска ренты (Tornell, Lane, 1999, Balanf, Francois, 2000, Torvik, 2002), механизма выработки экономической политики (Ross, 1999, Robinson et al., 2002) или изменчивости обменного курса (Gylfason et al., 1999).

Проблема «проклятия природных ресурсов» весьма актуальна не только для развивающихся стран, которым посвящен основной поток литературы, но и для стран с переходной экономикой, богатых природными ресурсами, в частности, России, Казахстана и Туркменистана. Сложность анализа экономических процессов в переходных экономиках состоит в том, что «нормальные» явления, свойственные рыночным экономикам, складываются здесь со специфическими фундаментальными изменениями, обусловленными переходом от плановой экономики (см. Матвеенко и др., 1998), однако, по мере развития рыночных отношений, в ресурсозависимых переходных экономиках становятся очевидными симптомы «голландской болезни».

Некоторые типичные проявления «голландской болезни» перечислены в таблице в Приложении. Эта таблица основана на основных западных публикациях в этой области, которые почти не затрагивают российскую экономику, вместе с тем из таблицы видно, насколько точно основные особенности современной российской экономики попадают под определение «голландской болезни».

Естественным шагом в изучении роли богатства природных ресурсов в экономическом развитии является исследование моделей роста с производственными функциями, включающими природные ресурсы как фактор производства. Вербальное рассмотрение моделей, включающих три фактора производства - труд, землю (вместе ее недрами) и капитал - и изучение распределения национального дохода между владельцами этих факторов было одним из центральных направлений классической политэкономии (А.Смит) и неоклассической экономики (Дж.Б.Кларк). Позднее Бруно (Bruno, 1984) в рамках трехфакторной модели с производственной функцией общего вида с постоянной отдачей от масштаба изучал краткосрочные и долгосрочные последствия для промышленно развитых стран повышения цен на сырье и энергоносители. Куралбаева и Эйсмонт (1999) на основе трехсекторной и двухсекторной моделей исследовали зависимость темпа роста ВВП ресурсоэкспортирующей страны от доли ресурсного сектора в экономике. Гилфасон и Зоега (Gylfason, Zoega, 2002) и Ситер (Seater, 2004) в односекторных моделях с трехфакторными функциями Кобба-Дугласа изучали влияние изменения долей факторов на стационарное состояние. В первой из этих работ в качестве третьего фактора производства выступали природные ресурсы, а во второй – человеческий капитал(3).

Основная цель данной работы – проанализировать в рамках односекторной модели влияние ресурсозависимости на темпы роста экономики. Мы будем рассматривать модель с трехфакторной производственной функцией Кобба-Дугласа(4) с постоянной отдачей от масштаба

(1)

Здесь - выпуск, - труд, - используемые природные ресурсы, - капитал, - доли труда, природных ресурсов и капитала, соответственно; . Переменная времени опускается, где возможно, для упрощения обозначений. Предполагается, что труд и использование природных ресурсов меняются с постоянными темпами прироста, равными и , соответственно:

Динамика капитала описывается уравнением

, (2)

где - потребление, - постоянный коэффициент износа.

Неоклассическая модель, где эластичности выпуска по факторам производства равны долям владельцев факторов в доходе, подразумевает совершенную конкуренцию на рынках факторов, в том числе на рынке природных ресурсов. Возможно. такое предположение является чрезмерным упрощением для моделирования российской экономики, однако, достоинство этой простой модели в том, что она ясно показывает возможный механизм отрицательного влияния ресурсозависимости на экономический рост.

Механизм «проклятия природных ресурсов» демонстрируемый моделью состоит в том, что при определенных условиях увеличение ресурсозависимости приводит к снижению процентной ставки (отдачи) на инвестиции в физический капитал, что вытесняет инвестиции из сектора обрабатывающей промышленности. В реальной экономике этому механизму соответствуют многие из проявлений «голландской болезни», перечисленных в таблице в Приложении. Сегодняшняя российская экономика вполне отвечает этим признакам.

Аналогичную модель изучали Гилфасон и Зоега (Gylfason, Zoega. 2002), но принципиальная новизна результатов в нашей работе состоит в том, что выявлена зависимость темпов роста (а не только уровней) от долей факторов. Кроме того, в ряде случаев мы исправляем выводы Гилфасона и Зоеги: имеет место сходимость траекторий модели Солоу (т.е. траекторий, для которых потребление как доля ВВП постоянно) и оптимальных траекторий модели Рамсея-Касса-Купманса не к стационарным состояниям

, а к сбалансированным траекториям

При решении задачи о влиянии изменения долей факторов на долгосрочные темпы экономического роста, мы проходим несколько этапов.

Сначала изучаются сбалансированные траектории моделей, описываемых только уравнением (2), без спецификации производственной

Функции. Здесь тематика нашего исследования пересекается с проблемой определения вида производственной функции, обеспечивающей движение по сбалансированной траектории, затронутой в недавней работе Джонса и Скримгеура (Jones, Scrimgeour, 2005).

Доказывается равенство между собой темпов прироста величин на сбалансированных траекториях, этот результат используется затем для вычисления этих темпов в модели с производственной функцией (1). Оказывается, что эти темпы зависят, в частности, от параметров (темпа прироста использования природных ресурсов) и b (доли природных ресурсов в доходе), которые отражают степень ресурсозависимости страны.

Затем мы находим сбалансированные траектории в моделях Солоу и Рамсея-Касса-Купманса и доказываем, что несбалансированные траектории-решения сходятся к сбалансированным траекториям. Также мы сравниваем сбалансированную траекторию золотого правила со сбалансированными траекториями модифицированного золотого правила для двух вариантов модели Рамсея-Касса-Купманса (со «стандартной» функцией полезности бесконечно живущего индивида и с предложенной Лукасом (Lucas, 1988) функцией полезности, учитывающей численность населения).

Наконец, мы исследуем влияние изменения значений параметров (темпа прироста использования природных ресурсов) и b (доли природных ресурсов в доходе) на темп прироста сбалансированных траекторий. Эти изменения параметров можно трактовать как изменение степени ресурсозависимости. Выясняются условия, при которых увеличение ресурсозависимости приводит к уменьшению темпов экономического роста.

Дальнейшая часть статьи организована следующим образом. В разделе 2 рассматриваются сбалансированные траектории моделей описываемых уравнением (2). В разделе 3 вычисляются темпы прироста на сбалансированных траекториях модели (1)-(2). В разделе 4 изучается переходная динамика (несбалансированные траектории) в модели Солоу, а в разделе 5 – в модели Рамсея-Касса-Купманса. В разделе 6 исследуется проблема влияния ресурсозависимости на темпы экономического роста. В разделе 7 обсуждаются проблемы, относяшиеся к российской экономике.

2. Сбалансированные траектории

Прежде всего, определим сбалансированные траектории. Пусть модель задана уравнением (2), и .

ПРЕДЛОЖЕНИЕ 1. Следующие три определения эквивалентны.

А. Траектория называется сбалансированной, если

(3)

(4)

Б. Траектория называется сбалансированной, если

В. Траектория называется сбалансированной, если

Равенство (3) представляет собой основную гипотезу модели Солоу (Solow, 1956). Равенство (4) – это один из пяти стилизованных фактов экономического роста, сформулированных Кальдором (Kaldor, 1961), этот факт входит в явном виде в формулировку AK-модели (Frankel, 1962). Равенство

(вместе с гипотезой о постоянном темпе роста труда) представляет еще один стилизованный факт Кальдора: душевой выпуск растет темпом, который примерно постоянен.

При доказательстве предложения 1 будет использоваться следующая лемма.

ЛЕММА 1. Если величины - ненулевые, имеют постоянные темпы, и

,

то их темпы роста совпадают.

ДОКАЗАТЕЛЬСТВО ЛЕММЫ. Предположим противное:

,

.

Пусть, для определенности, . Тогда

.

При , левая часть равенства стремится к постоянной , тогда как модуль правой части стремится к 0 или к . Полученное противоречие показывает, что ■

ДОКАЗАТЕЛЬСТВО ПРЕДЛОЖЕНИЯ. АБ. Из (2) следует, что

Здесь правая часть постоянна, следовательно

, тогда (в силу (4)) и (в силу (3)).

БВ. Из (2) следует, что

.

Левая часть постоянна, а слагаемые в правой части имеют постоянные темпы прироста. По лемме, темпы прироста величин

равны, следовательно, Поскольку , из (2) вытекает, что

В этом равенстве правая и левая части имеют постоянные темпы прироста, следовательно, эти темпы совпадают:

ВА. Очевидно ■

Обозначим общий темп прироста переменных на сбалансированной траектории через . Следствием предложения 1 является следующее утверждение, которое можно рассматривать как обобщение теоремы Узавы (см. далее предложение 3). Введем обозначение .

ПРЕДЛОЖЕНИЕ 2. Всякая сбалансированная траектория может быть построена при помощи двухфакторной производственной функции с трудосберегающим техническим прогрессом

(5)

где G – неоклассическая функция (т.е. обладающая стандартными свойствами производственной функции, в частности, имеющая постоянную отдачу от масштаба – CRS). При этом темп прироста технического прогресса совпадает с темпом прироста душевого дохода:

ДОКАЗАТЕЛЬСТВО. Пусть – произвольная неоклассическая функция. Можно подобрать число так, что

.

Пусть

Тогда на сбалансированной траектории

по свойству CRS

по предложению 1

■

Таким образом, если модель задана посредством некоторой CRS производственной функции F, то на сбалансированной траектории может действовать также и другая CRS производственная функция G любого вида с трудосберегающим техническим прогрессом. Отсюда следует невозможность однозначного выбора производственной функции, если наблюдаемая траектория - сбалансированная.

Заметим, что полученное в предложении 2 представление G производственной функции не связано со структурой изначально заданной функции F. На сбалансированной траектории значения функций F и G совпадают, однако функция G не наследует никаких других свойств функции F.

Смысл предложения 2 весьма прозрачен. Как следует из предложения 1, на сбалансированной траектории капитал и выпуск растут общим темпом, а рост труда «не дотягивает» до этого темпа. Если технический прогресс придаст эффективному труду необходимую добавку темпа, то капитал и эффективный труд будут расти одним темпом, что обеспечит роста выпуска тем же темпом.

Вид (5) – не единственный вид производственной функции, который приводит к данной сбалансированной траектории. Например, ту же сбалансированную траекторию может определять функция Леонтьева или производственная функция AK-модели

где

Такого рода неоднозначность уменьшается, если ограничить множество сбалансированных траекторий условием постоянства долей факторов.

ПРЕДЛОЖЕНИЕ 3 (Теорема Узавы – см. Uzawa, 1961, Jones, Scrimgeour, 2005). Если модель определена непрерывно дифференцируемой CRS производственной функцией , и на сбалансированной траектории доли факторов

постоянны во времени(5), то (5) – единственно возможное представление производственной функции F на этой траектории.

Доказательство см. в Jones, Scrimgeour, 2005■

Хотя предложение 3 сужает, по сравнению с предложением 2, класс производственных функций, пригодных для построения сбалансированной траектории, оно не позволяет выявить вид функции F вне этой траектории. Т.е. невозможно однозначно специфицировать производственную функцию, наблюдая лишь одну сбалансированную траекторию.

Пусть, например,

- сбалансированная траектория,

- известные доли капитала и труда на этой траектории, и мы хотим специфицировать CES функцию

В таком случае начальный уровень технического прогресса и параметры CES функции удовлетворяют системе уравнений

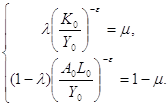
Однако, тройка определяется этой системой неоднозначно.

Особенность двухфакторной функции Кобба-Дугласа в том, что для нее множитель может трактоваться не только как трудосберегающий (нейтральный по Харроду) технический прогресс, но еще и как капиталосберегающий (нейтральный по Солоу) и как увеличивающий TFP (нейтральный по Хиксу) прогресс:

.

Поэтому теорему Узавы формулируют еще так: если на сбалансированной траектории доли факторов постоянны, то либо имеет место трудосберегающий технический прогресс, либо действует производственная функция Кобба-Дугласа.

Применительно к трехфакторной функции с природными ресурсами предложение 2 может быть переформулировано следующим образом.

ПРЕДЛОЖЕНИЕ 4. Пусть сбалансированная траектория такова, что . Тогда эта траектория может быть построена при помощи трехфакторной производственной функции с трудосберегающим и ресурсосберегающим техническим прогрессом

, (6)

где , G – неоклассическая функция.

ДОКАЗАТЕЛЬСТВО. Аналогично доказательству предложения 2, для произвольной CRS функции G подберем числа так, что

.

Определим функции

Тогда на сбалансированной траектории

по свойству постоянной отдачи от масштаба

по предложению 1

■

Обобщением теоремы Узавы для случая трехфакторной модели является следующее утверждение.

ПРЕДЛОЖЕНИЕ 5. Если модель определена непрерывно дифференцируемой CRS производственной функцией

и на сбалансированной траектории доли факторов

постоянны во времени, то (6) – единственно возможное представление производственной функции на этой траектории.

ДОКАЗАТЕЛЬСТВО. Введем обозначения

Заметим, что при экзогенно заданных

траектория

определена последовательностью (восстанавливается по этой последовательности), таким образом можно представить траекторию как

.

На произвольной траектории в момент t, эластичность y по x равна отношению доли капитала к суммарной доли остальных двух факторов:

. (7)

Действительно,

следовательно

,

отсюда

,

т.е.

,

откуда следует (7).

В силу предложения 1, на сбалансированной траектории величина

сохраняется

На сбалансированной траектории с постоянными долями факторов имеет место равенство

.

Решая это дифференциальное уравнение, получаем

,

где - некоторые функции. Отсюда, аналогично тому, как это сделано в Jones, Scrimgeour, 2005 для двухфакторной производственной функции, можно получить, что

.

Поскольку труд и используемые природные ресурсы входят в формулировку модели симметрично, функция также сепарабельна, т.е.

■

Для функции Кобба-Дугласа

технический прогресс можно трактовать как трудо- и ресурсосберегающий одновременно, но еще и как только трудосберегающий, только ресурсосберегающий, а также как капиталосберегающий или как увеличивающий TFP.

Функция CES

обладает тем достоинством, что доли факторов на сбалансированной траектории постоянны, если прогресс является трудосберегающим и ресурсосберегающим. Действительно, пусть

,

Тогда доля труда на сбалансированной траектории равна

Аналогично проверяется постоянство доли природных ресурсов на сбалансированной траектории.

3. Темпы прироста на сбалансированных траекториях

Пусть выпуск описывается производственной функцией (1), и общая производительность факторов A, труд L и использование природных ресурсов N меняются постоянными темпами, равными , и , соответственно. Вычислим темп прироста на сбалансированной траектории.

ПРЕДЛОЖЕНИЕ 6. На любой сбалансированной траектории

.

ДОКАЗАТЕЛЬСТВО. Равенство между собой темпов прироста величин доказано в предложении 1. Запишем производственную функцию (1) в темпах прироста:

.

Отсюда находим ■

Приведем также ВТОРОЕ ДОКАЗАТЕЛЬСТВО ПРЕДЛОЖЕНИЯ 6. Следуя трехфакторному варианту теоремы Узавы (предложению 5), обозначим через и вносимые техническим прогрессом добавки к темпам прироста труда и природных ресурсов, соответственно, которые обеспечивают движение по сбалансированной траектории. Имеет место система уравнений:

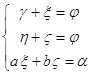
Отсюда находим , а также

■

В более общем случае, когда - дифференцируемая производственная функция с постоянной отдачей от масштаба по первым трем переменным, предложение 6 обобщается следующим образом.

ПРЕДЛОЖЕНИЕ 7. На любой сбалансированной траектории

где темп технического прогресса определен как

доли труда и ресурсов– как эластичности

,

доля капитала равна

(Значения переменных берутся в точке на сбалансированной траектории)

ДОКАЗАТЕЛЬСТВО. Имеем

,

откуда

.

С учетом предложения 1,

.

Отсюда, используя теорему Эйлера, получаем

■

Таким образом, в случае функции Кобба-Дугласа (1), темп прироста величин - один и тот же на всех сбалансированных траекториях. Он определяется темпами роста первичных факторов (труда и используемых природных ресурсов) и темпом изменения TFP, а также долями факторов в доходе (эластичностями выпуска по факторам).

Значения (потребление как доля ВВП) и (капиталоотдача) различаются на сбалансированных траекториях, они зависят от начального значения капитала при данных значениях .

Находим

и, с учетом (2),

, (8)

.

По определению А в предложении 1, каждая сбалансированная траектория является траекторией Солоу. Вычислим для нее норму накопления:

. (9)

Теперь мы хотим сравнить между собой различные сбалансированные траектории с одинаковыми начальными , чтобы понять, какая из них лучше с точки зрения потребления.

Поскольку сбалансированные траектории не отличаются темпами роста, сбалансированная траектория, которая имеет наибольший уровень потребления в начальный момент времени, имеет его и в дальнейшем при любом t среди всех сбалансированных траекторий с данными

.

Из (8) следует, что

Максимум по достигается при

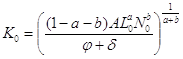
Соответствующая сбалансированная траектория имеет вид

,

,

где

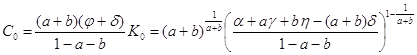
Как следует из (9), для этой сбалансированной траектории норма накопления равна

.

Можно назвать эту траекторию сбалансированной траекторией золотого правила.

Предельный продукт капитала на сбалансированной траектории золотого правила равен

,

т.е., как и в стандартной модели Солоу, золотое правило состоит в равенстве

предельного продукта капитала сумме темпа прироста и коэффициента износа.

Подчеркнем, что стационарного состояния в смысле

в рассматриваемой модели не существует, поскольку капитал и труд имеют разные темпы роста на сбалансированной траектории. Как и в стандартной модели Солоу с трудосберегающим техническим прогресом с двухфакторной производственной функцией, можно рассматривать стационарное состояние вида

где - эффективный труд. Однако, мы введем новые фазовые траектории другим способом, аналогично тому, как это сделано в Lucas, 1988.

Поскольку в нашей модели действует единый темп прироста на всех сбалансированных траекториях, естественно ввести фазовые переменные

.

При этом каждая сбалансированная траектория превращается в точку на фазовой плоскости

На любой траектории (не обязательно сбалансированной)

.

Справедливы равенства

.

Уравнение (2) превращается в

. (10)

4. Несбалансированные траектории Солоу

Как видно из определения А в предложении 1, всякая сбалансированная траектория является траекторией Солоу (т.е. траекторией, на которой потребление составляет постоянную долю выпуска). Покажем, что, наоборот, всякая траектория Солоу является асимптотически сбалансированной.

На траектории Солоу с нормой накопления

, уравнение (10) принимает вид

.

Отсюда находим для траектории Солоу стационарное фазовое состояние

и темп прироста фазовой переменной :

Видим, что стационарное фазовое состояние глобально устойчиво, причем темп прироста уменьшается по модулю по мере приближения фазовой траектории к .

Что же касается самой траектории Солоу в переменных

то она является асимптотически сбалансированной. Поскольку

темп прироста изменяется монотонно и приближается к .

Ошибочно полагать (как это делают Гилфасон и Зоега), что для траектории Солоу имеет место сходимость к стационарному состоянию по переменной . Переменные растут асимптотически разными темпами, за исключением случая, когда совпадают темпы экзогенных переменных .

5. Траектории модели Рамсея-Касса-Купманса

Сформулируем задачу поиска оптимальной траектории:

,

(2)

, , (1)

,

заданы

Применяя принцип максимума Л.С.Понтрягина, построим гамильтониан текущего значения

и выпишем условия оптимальности

, (11)

, (12)

а также (2).

Условие (11) дает

,

отсюда и из (12) следует, что

В частности, рассмотрим случай

Тогда

и мы приходим к системе дифференциальных уравнений

, (2)

При переходе к фазовым переменным , эта система превращается в

, (10)

.

Стационарное фазовое состояние равно

,

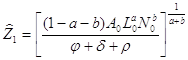Ему соответствует сбалансированная траектория, для которой

,

ее можно назвать сбалансированной траекторией модифицированного золотого правила.

Матрица Якоби в точке имеет вид

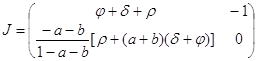
Определитель этой матрицы отрицателен, следовательно, стационарное фазовое состояние представляет собой седловую точку. Таким образом, оптимальные траектории-решения задачи Рамсея-Касса-Купманса при данных начальных сходятся асимптотически к сбалансированной траектории модифицированного золотого правила.

Норма накопления на сбалансированной траектории модифицированного золотого правила, согласно (9), равна

.

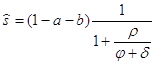Видим, что норма накопления отрицательно зависит от нормы дисконтирования (более терпеливое общество сберегает больше) и положительно связана с темпом роста .

Норма накопления и капитал на сбалансированной траектории модифицированного золотого правила при любой норме дисконтирования оказываются меньше, чем на сбалансированной траектории золотого правила, т.е. долгосрочное качество сбалансированной траектории модифицированного золотого правила всегда хуже. Это можно объяснить выбором критерия оптимальности. При данном интегральном критерии, цель фактически состоит не в оптимальном устойчивом (т.е. долгосрочном) росте, а в обеспечении максимального дисконтированного потребления на относительно близком промежутке времени: «хвост» интеграла имеет слишком малый вес, чтобы влиять существенно на выбор траектории.

Ситуация меняется, если использовать критерий оптимальности, аналогичный тому, которым пользовался Лукас (Lucas, 1988):

Тогда условие оптимальности (11) меняется на

Откуда

,

.

В случае, когда

приходим к системе дифференциальных уравнений

, (2)

,

которая, при переходе к фазовым переменным , превращается в

, (10)

.

Стационарное фазовое состояние равно

,

,

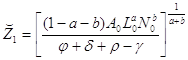а норма накопления

.

Видим, что при сбалансированная траектория модифицированного золотого правила совпадает со сбалансированной траекторией золотого правила. Это условие состоит в равенстве субъективной нормы дисконтирования «биологической процентной ставке», о которой писал Самуэльсон (Samuelson, 1958), рассматривая модель перекрывающихся поколений. При (нетерпеливое общество) норма накопления и капитал меньше, чем при золотом правиле Солоу, а при (терпеливое общество) – больше. Заметим, что в терпеливом обществе предельный продукт капитала меньше, чем в нетерепеливом обществе, т.е. причиной повышенных инвестиций в терпеливом обществе является не более высокая процентная ставка, а иные межвременные предпочтения.

6. Ресурсозависимость и снижение темпа роста

Как известно, основной вывод из анализа неоклассических моделей с двухфакторными производственными функциями (таких как модель Солоу и модель Рамсея-Касса-Купманса) состоит в том, что долгосрочный темп роста при отсутствии технического прогресса совпадает с темпом роста населения. При наличии трудосберегающего технического прогресса, его темп добавляется к темпу прироста экономики.

Модель с трехфакторной производственной функцией, как мы видим, дает иной результат: темп роста зависит не только от темпов роста первичных факторов производства (труда и используем