Виявлення грубих результатів вимірювань
Виявлення грубих результатів вимірювань
При використанні статистичних методів для оцінки результату і характеристик випадкових похибок вимірювань за вибіркою (серією, рядом) результатів спостережень обмеженого об’єму повинна виконуватися вимога однорідності цієї вибірки, тобто приналежність усіх її членів до однієї генеральної сукупності. Проте на практиці дана вимога часто порушується, оскільки до складу вибірки можуть входити результати спостережень, які мають грубі похибки і промахи, що може призвести до істотного викривлення результату вимірювань і його похибки.
При попередньому перегляді результатів спостережень експериментатор мусить діяти так. Якщо є результати спостережень (звичайно один-два), які різко відрізняються від інших, то слід уважно проаналізувати, чи не допущена помилка при знятті показів ЗВТ або їх записі. Коли експериментатор переконався, що дані результати є промахами, то вони вилучаються з подальшого розгляду. В противному разі, тобто якщо не вдається підтвердити, що підозрілі результати належать до промахів, необхідно перевірити, чи не викликані сумнівні результати спостережень грубими похибками. Така сама перевірка необхідна і в тому випадку, коли експериментальні дані одержані автоматично, а також за умови, що їх обробка виконується через деякий час після закінчення експерименту.
Для виявлення грубих результатів (похибок) вимірювань використовують статистичні критерії.
При умові, що вимоги до точності результатів прямих вимірювань невисокі, можна користуватися найпростішим критерієм, яким є "правило ![]() ". Його сутність полягає в тому, що для вибірки
". Його сутність полягає в тому, що для вибірки ![]() обчислюється оцінка СКВ
обчислюється оцінка СКВ ![]() і всі результати спостережень, які задовольняють умову
і всі результати спостережень, які задовольняють умову ![]() , визнаються такими, що мають грубі похибки. Дане правило в ряді випадків є надмірно "жорстким". Так, якщо для нормального розподілу поява результату спостереження
, визнаються такими, що мають грубі похибки. Дане правило в ряді випадків є надмірно "жорстким". Так, якщо для нормального розподілу поява результату спостереження ![]() свідчить про наявність у ньому грубої похибки, то для рівномірного розподілу аналогічний висновок відповідає умові
свідчить про наявність у ньому грубої похибки, то для рівномірного розподілу аналогічний висновок відповідає умові ![]() . Це означає, що критерій виявлення грубих похибок повинен ураховувати не тільки степінь розсіювання результатів вимірювань, яке характеризується значенням СКВ
. Це означає, що критерій виявлення грубих похибок повинен ураховувати не тільки степінь розсіювання результатів вимірювань, яке характеризується значенням СКВ ![]() , але й вид розподілу випадкових похибок.
, але й вид розподілу випадкових похибок.
Для виявлення грубих похибок результатів вимірювань, які підпорядковуються нормальному розподілу, широке розповсюдження знаходить критерій, що ґрунтується на порівнянні теоретичного (або граничного) і експериментального (або фактичного) значень параметра t, який характеризує найбільше відхилення результатів спостережень ![]() від середнього арифметичного
від середнього арифметичного ![]() .
.
Методика застосування цього критерію така.
1. Складають упорядкований (варіаційний) ряд результатів спостережень, розмістивши вихідні елементи ряду в порядку зростання (убування) і виконавши їх перенумерування, наприклад, ![]() .
.
2. Для початкового ряду результатів спостережень обчислюють значення середнього арифметичного ![]() і незміщеної оцінки СКВ
і незміщеної оцінки СКВ ![]() згідно з формулами (2.13) і (2.19).
згідно з формулами (2.13) і (2.19).
3. Для крайніх членів упорядкованого ряду, які найбільш віддалені від центра розподілу (визначається як середнє арифметичне ![]() цього ряду) і тому з найбільшою ймовірністю можуть мати грубі похибки, обчислюють відношення
цього ряду) і тому з найбільшою ймовірністю можуть мати грубі похибки, обчислюють відношення
![]()
де ![]() та
та ![]() .
.
4. За таблицею значень ![]() (додаток 10), входом якої є заданий рівень значущості
(додаток 10), входом якої є заданий рівень значущості ![]() і число елементів вибірки n, знаходять теоретичне значення
і число елементів вибірки n, знаходять теоретичне значення ![]() і порівнюють його з обчисленим у п. 3 значенням t. Якщо виявиться, що
і порівнюють його з обчисленим у п. 3 значенням t. Якщо виявиться, що ![]() , то відповідний результат спостереження
, то відповідний результат спостереження ![]() або
або ![]() , повинен бути вилучений з подальшої обробки як грубий.
, повинен бути вилучений з подальшої обробки як грубий.
Потім пп. 2-4 повторюють для (n-1) елементів вибірки до тих пір, доки умова ![]() не перейде в умову
не перейде в умову ![]() . Проте при невеликій кількості спостережень, принаймні при
. Проте при невеликій кількості спостережень, принаймні при ![]() , указана методика може призвести до невірної оцінки грубої похибки і, як наслідок, до помилкового вилучення результату спостереження
, указана методика може призвести до невірної оцінки грубої похибки і, як наслідок, до помилкового вилучення результату спостереження ![]() , який насправді не є грубим.
, який насправді не є грубим.
2.8. Методи вилучення систематичних похибок з результатів вимірювань
Систематичні похибки, незалежно від характеру їх змінювання в часі при постановці і проведенні вимірювального експерименту, повинні бути виявлені і вилучені з результатів вимірювань або хоча б зменшені, для чого важливо знати джерела і причини їх виникнення. За цією ознакою розрізняють такі систематичні похибки: похибку через неадекватність об’єкта і фізичної моделі вимірювання; похибки методу вимірювання і ЗВТ; похибки, обумовлені дією впливних величин, і суб’єктивну похибку оператора. Систематичні похибки можуть бути викликані одночасно декількома причинами, які треба враховувати при організації вимірювального експерименту і виробленні заходів щодо їх вилучення.
Наведемо основні методи вилучення або зменшення систематичних похибок результатів вимірювань.
1. Застосування спеціальних конструктивних і схемотехнічних рішень, направлених на ослаблення або усунення дії на систематичну похибку ЗВТ впливних величин. Наприклад, термостатування і теплоізоляція ЗВТ або окремих його вузлів з метою зменшення температурної похибки, екранування для захисту від зовнішніх електромагнітних полів, застосування спеціальних фундаментів і віброгасних пристроїв для ослаблення впливу механічних дій, застосування спеціальних схемотехнічних рішень при розробці найбільш критичних до дії зовнішніх факторів вузлів ЗВТ та їх виготовлення з високостабільних комплектуючих елементів.
2. Вилучення методичної систематичної похибки аналітичним шляхом на основі розрахунку її значення, виходячи з особливостей застосованого при експерименті методу вимірювань і характеристик ЗВТ.
3. Використання методу заміщення для виключення інструментальної похибки вимірювань, яка обумовлена вимірювальним приладом. При цьому вимірювання виконуються за два етапи. Спочатку на вхід вимірювального приладу подається вимірювана фізична величина і фіксується показ приладу. Потім до входу вимірювального приладу приєднується вихід регульованої зразкової міри, яка відтворює фізичну величину, однорідну з вимірюваною і, регулюючи міру, добиваються того ж показу приладу. Результат вимірювання, вільний від систематичної похибки, зчитується з відлікового пристрою міри.
Прикладом вилучення систематичної похибки за допомогою методу заміщення служить вимірювання активного опору ![]() омметром, який має постійну систематичну похибку, в тому числі за рахунок з’єднувальних проводів. Результат вимірювання опору омметром подамо у вигляді
омметром, який має постійну систематичну похибку, в тому числі за рахунок з’єднувальних проводів. Результат вимірювання опору омметром подамо у вигляді ![]() , де
, де ![]() - систематична похибка омметра. Після цього замість вимірюваного опору
- систематична похибка омметра. Після цього замість вимірюваного опору ![]() до омметра приєднується магазин опору, змінюванням опору
до омметра приєднується магазин опору, змінюванням опору ![]() якого добиваються того ж показу омметра
якого добиваються того ж показу омметра ![]() . При постійній систематичній похибці омметра
. При постійній систематичній похибці омметра ![]() для результатів двох вимірювань (а вони однакові й дорівнюють
для результатів двох вимірювань (а вони однакові й дорівнюють ![]() ) виконується умова
) виконується умова ![]() , звідки
, звідки ![]() , тобто відлік результату вимірювання опору
, тобто відлік результату вимірювання опору ![]() здійснюється з магазина опору, а постійна систематична похибка омметра
здійснюється з магазина опору, а постійна систематична похибка омметра ![]() вилучається.
вилучається.
4. Застосування методу компенсації систематичної похибки за знаком. Метод дозволяє вилучити постійну систематичну похибку, яка обумовлена впливною величиною і характеризується не тільки її значенням, але й напрямом. Для цього необхідно провести два вимірювання величини X таким чином, щоб систематична похибка ![]() , залишаючись незмінною за модулем, увійшла в результати вимірювань
, залишаючись незмінною за модулем, увійшла в результати вимірювань ![]() з різними знаками:
з різними знаками: ![]() і
і ![]() . Тоді результат вимірювання визначається середнім значенням
. Тоді результат вимірювання визначається середнім значенням
![]()
Такий варіант методу компенсації за знаком використовується, зокрема, для вилучення систематичних похибок, обумовлених впливом зовнішніх постійних магнітних полів або термоЕРС, у цифрових фазометрах двопівперіодної дії (з усередненням двох результатів вимірювань, виконаних через півперіоду вхідних сигналів). Різновидом методу компенсації є метод періодичних спостережень, який дозволяє вилучити періодичну систематичну похибку. Його суть зводиться до того, що вимірювання проводять парне число разів через інтервали часу, що дорівнюють півперіоду змінювання систематичної похибки, а результат вимірювання знаходять усередненням одержаних результатів.
5. Застосування методу протиставлення, який також передбачає дворазове вимірювання розміру фізичної величини. При цьому умови експериментів повинні відрізнятися так, щоб за відомими закономірностями систематичної похибки можна було б її вилучити. Прикладом цього методу може служити вимірювання активного опору ![]() за схемою моста постійного струму (рис. 2.5), для якої результат вимірювання визначається з умови рівноваги
за схемою моста постійного струму (рис. 2.5), для якої результат вимірювання визначається з умови рівноваги ![]() .
.
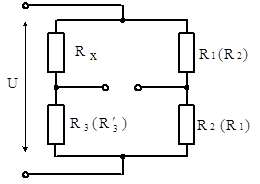
)Рис.2.5. До пояснення вилучення систематичної похибки вимірювань
за допомогою метода протиставлення
Результат вимірювання ![]() може включати в себе систематичну похибку внаслідок відмінності опорів резисторів
може включати в себе систематичну похибку внаслідок відмінності опорів резисторів ![]() від їх номінального значення. Цю похибку можна вилучити, якщо резистори R1 і R2 поміняти місцями і знову зрівноважити міст тільки резистором R3. З умови рівноваги моста одержимо
від їх номінального значення. Цю похибку можна вилучити, якщо резистори R1 і R2 поміняти місцями і знову зрівноважити міст тільки резистором R3. З умови рівноваги моста одержимо ![]() , де
, де ![]() - опір резистора R3 при новій рівновазі моста. Підставивши відношення
- опір резистора R3 при новій рівновазі моста. Підставивши відношення ![]() , знайдене з однієї умови рівноваги моста, в іншу умову його рівноваги, одержимо
, знайдене з однієї умови рівноваги моста, в іншу умову його рівноваги, одержимо ![]() . Таким чином, із результату вимірювання
. Таким чином, із результату вимірювання ![]() виключається відношення опорів
виключається відношення опорів ![]() , а отже, і систематична похибка, що вноситься резисторами R1 і R2.
, а отже, і систематична похибка, що вноситься резисторами R1 і R2.
6. Проведення повірки ЗВТ з метою визначення систематичної похибки та її компенсації уведенням поправки в результат вимірювання. Цей метод застосовується для вилучення постійних у часі систематичних похибок, що мають ЗВТ, в окремих позначках шкали.
У сучасних ЗВТ, особливо в програмно-керованих, для визначення поправок або коригувальних коефіцієнтів усе ширше використовується калібрування від внутрішнього, інколи зовнішнього калібратора, який являє собою або джерело зразкового (опорного) сигналу з параметрами, заданими з високою точністю, або зразкові елементи (резистори, конденсатори). Калібрування здійснюється в декількох точках діапазону вимірювань, для кожної з них визначається поправка (або коригувальний коефіцієнт) і всі їх значення записують в ОЗП ЗВТ. Потім результат вимірювання уточнюється за допомогою поправки або коригувального коефіцієнта.
Таким чином, у принципі, систематичні похибки вимірювань можуть бути передбачені, виявлені і тому є можливість для їх повного вилучення з результату вимірювання, тобто перейти до виправленого результату вимірювання. Проте, використовуючи на практиці описані методи вилучення систематичних похибок, слід пам’ятати, що повною мірою добитися цієї мети не можна. Отже, будь-який виправлений результат вимірювання має деякий залишок систематичної похибки, названий невилученою систематичною похибкою, що є випадковою величиною, оцінювання характеристик якої ґрунтується на методах математичної статистики.
Інколи для підвищення правильності вимірювань, тобто зменшення систематичних похибок, використовують рандомізацію. Під рандомізацією розуміють штучне переведення систематичних похибок у випадкові (в перекладі з англійської термін "рандомізація" означає перемішування, створення хаосу). Для здійснення рандомізації процес вимірювання організується так, щоб фактори, які впливають на результати вимірювань, а точніше, на їх похибки, діяли випадково. Наприклад, неточне градуювання шкали вимірювального приладу призводить до появи систематичних похибок для даного приладу. Якщо ж вимірювання самої фізичної величини провести декількома приладами даного типу, то ці похибки будуть змінюватися від приладу до приладу випадково. Піддаючи одержані результати спостережень статистичній обробці, можна істотно зменшити систематичну складову результату вимірювання.
2.9. Методи підсумовування похибок вимірювань
2.9.1. Постановка задачі підсумовування похибок вимірювань
При аналізі похибок вимірювань і ЗВТ можливі три основні задачі:
1) кількісна оцінка окремих складових систематичної і випадкової похибок;
2) підсумовування кількісних характеристик складових похибки одного виду (систематичних або випадкових);
3) підсумовування кількісних характеристики систематичної і випадкової складових з метою одержання повної похибки.
Вирішення цих задач у сукупності і дозволяє одержати кількісні оцінки характеристик похибки, тобто оцінити похибку. Перш за все зауважимо, що термін "підсумовування" використовують при оцінюванні похибок в узагальненому смислі, а не як найменування конкретної математичної операції. Більш того, в останній час замість терміна "підсумовування" все частіше застосовують термін "об’єднання" похибок.
Повна похибка вимірювань, як і ЗВТ, у загальному випадку створюється рядом складових (систематичних і випадкових), оцінку кожної з яких знаходять розрахунковим або експериментальним шляхом. Метод підсумовування складових похибки визначається природою і взаємозв’язком їх джерел.
Сутність задачі визначення розрахунковим шляхом повної похибки вимірювань або ЗВТ полягає в підсумовуванні (об’єднанні) її окремих складових за установленим, загальноприйнятим правилом, що є одним із заходів забезпечення єдності вимірювань. Так, для визначення похибки навіть окремого вимірювального пристрою необхідно підсумовувати всі його складові похибки, викликані різними причинами. При створенні вимірювальних приладів, установок і систем має місце задача оцінки похибки вимірювальних каналів, яка зводиться до підсумовування похибок ряду вимірювальних пристроїв, що створюють даний вимірювальний канал. Для визначення похибок будь-яких видів вимірювань необхідно підсумовувати різні складові методичних, інструментальних і суб’єктивних похибок, а також похибку обчислювань при опосередкованих, сукупних і сумісних вимірюваннях.
Таким чином, задача розрахункового підсумовування (або аналітичного визначення) похибок - одна з основних задач як при створенні ЗВТ, так і при оцінюванні похибок результатів вимірювань. Причому необхідні якомога простіші методи підсумовування похибок.
Трудність підсумовування похибок полягає в тому, що всі складові похибки треба розглядати як випадкові величини з найрізноманітнішими значеннями в кожній конкретній реалізації. Найбільш повно вони можуть бути описані своїми законами розподілу, а їх спільна дія - композицією цих законів. Проте вирішення задачі підсумовування похибок у такій постановці пов’язане з великими труднощами двоякого роду. По-перше, одержання композиції законів розподілу похибок уже для 3-4 складових вимагає значного об’єму обчислювань, які часто можуть бути виконані тільки на ЕОМ. По-друге, при виконанні технічних і більшості контрольно-повірочних вимірювань експериментатор, як правило, не має інформації про закони розподілу складових сумарної похибки. Ці труднощі викликають необхідність застосування для оцінювання похибок спрощених правил підсумовування їх складових, які дозволяють з достатнім ступенем вірогідності оцінити сумарну похибку в умовах неповної початкової інформації.
Найбільш розробленими методами оцінювання випадкових похибок є методи, які безпосередньо запозичені з математичної статистики. Основні труднощі складають оцінювання і підсумовування систематичних похибок. Звичайно їх характеризують границями, які оцінюють приблизними методами, в тому числі близькими до статистичних.
Для оцінювання похибок використовуються три методи (правила, види, форми) підсумовування складових похибок: арифметичне, алгебраїчне і геометричне (квадратичне, статистичне) підсумовування.
2.9.2. Визначення сумарної систематичної похибки вимірювань
При точних вимірюваннях багато які систематичні похибки вилучаються або відповідною постановкою експерименту, або введенням поправок. Як правило, це легше зробити для змінних похибок, які так чи інакше проявляються у вимірювальних сигналах (показах) ЗВТ. Трудніше вилучити постійні систематичні похибки: потрібен аналіз даних про об’єкт, засоби і умови вимірювань, як апріорних, так і одержаних під час експерименту. Це є однією з основних задач при проведенні вимірювань. Методи їх вирішення не достатньо формалізовані і потребують високої метрологічної культури.
Постійні систематичні похибки можна поділити на строго і умовно постійні, причому способи оцінювання і підсумовування для них різні. Для строго постійних складових придатний лише детерміністський підхід і відповідно алгебраїчне та арифметичне підсумовування. Для умовно постійних складових систематичної похибки придатні, залежно від умов, різні квазістатистичні способи підсумовування.
Для визначення систематичної складової повної похибки, інакше кажучи, при підсумовуванні постійних систематичних складових похибки, коли відомі їх значення і знаки, використовують алгебраїчне підсумовування. Це правило є наслідком однієї з основних властивостей математичного сподівання випадкових величин, згідно з яким математичне сподівання суми випадкових величин (похибок) дорівнює сумі математичних сподівань цих випадкових величин (похибок). Ураховуючи, що математичне сподівання повної похибки являє собою її систематичну складову, маємо алгебраїчну суму
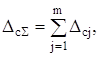
де ![]() - сумарна систематична похибка;
- сумарна систематична похибка;
![]() - складові систематичної похибки,
- складові систематичної похибки, ![]() - їх кількість.
- їх кількість.
Якщо для строго постійних систематичних похибок задані їх допустимі значення (або границі змінювання) ![]() , то визначається допустиме значення сумарної систематичної похибки як арифметична сума за модулем допустимих значень складових
, то визначається допустиме значення сумарної систематичної похибки як арифметична сума за модулем допустимих значень складових
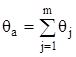 .
.
Величину ![]() називають арифметичними границями систематичної похибки.
називають арифметичними границями систематичної похибки.
На практиці нерідко буває відома додаткова інформація про поведінку систематичних похибок, зокрема, відомо, що невилучені систематичні похибки змінюються нерегулярно, залишаючись у границях ![]() . Тоді при підсумовуванні такі похибки умовно розглядають як випадкові величини і звичайно вважають, що вони рівномірно розподілені в заданих границях. Це припущення ґрунтується на тому, що для випадкової величини, яка змінюється в заданих границях, рівномірному розподілу відповідає максимальна ентропія (невизначеність). Тому таке припущення є досить обережним і на практиці приводить до реалістичної оцінки похибок.
. Тоді при підсумовуванні такі похибки умовно розглядають як випадкові величини і звичайно вважають, що вони рівномірно розподілені в заданих границях. Це припущення ґрунтується на тому, що для випадкової величини, яка змінюється в заданих границях, рівномірному розподілу відповідає максимальна ентропія (невизначеність). Тому таке припущення є досить обережним і на практиці приводить до реалістичної оцінки похибок.
Зрозуміло, цей умовний прийом не є єдино можливим, проте він досить простий і широко застосовується на практиці. Можна використовувати і "нестатистичні" методи, які базуються, наприклад, на інтервальному аналізі або теорії нечітких множин, проте ці методи не є строго обґрунтованими і містять певні припущення (8).
При квазістатистичному методі границі ![]() довірчого інтервалу сумарної невилученої систематичної похибки
довірчого інтервалу сумарної невилученої систематичної похибки ![]() називають статистичними і знаходять за формулою
називають статистичними і знаходять за формулою
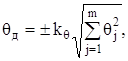 (2.22)
(2.22)
де ![]() - коефіцієнт, що залежить від числа m складових невилученої систематичної похибки і від співвідношення їх границь, а також від довірчої ймовірності P. Формула (2.22) є приблизною, вона одержана шляхом побудови композиції рівномірних розподілів складових
- коефіцієнт, що залежить від числа m складових невилученої систематичної похибки і від співвідношення їх границь, а також від довірчої ймовірності P. Формула (2.22) є приблизною, вона одержана шляхом побудови композиції рівномірних розподілів складових ![]() на відповідних інтервалах
на відповідних інтервалах ![]() . Значення коефіцієнта
. Значення коефіцієнта ![]() для трьох поширених значень P наведено в табл. 2.2.
для трьох поширених значень P наведено в табл. 2.2.
При значеннях довірчої ймовірності ![]() та
та ![]() залежність коефіцієнта
залежність коефіцієнта ![]() від числа складових m незначна, тому рекомендується брати середні значення коефіцієнта
від числа складових m незначна, тому рекомендується брати середні значення коефіцієнта ![]() :
: ![]()
![]() . При
. При ![]() залежність коефіцієнта
залежність коефіцієнта ![]() від числа складових m та їх співвідношення істотні, тому при
від числа складових m та їх співвідношення істотні, тому при ![]() рекомендується брати значення
рекомендується брати значення ![]() , а при
, а при ![]() можна уточнювати значення
можна уточнювати значення ![]() за графіком (наводиться в окремих працях) або за допомогою табл. 2.3.
за графіком (наводиться в окремих працях) або за допомогою табл. 2.3.
Таблиця 2.2
| Довірча ймовірність, P | Значення коефіцієнта | ||||||
| 2 | 3 | 4 | 5 | ... | ¥ | Середнє | |
| 0,90 | 0,97 | 0,96 | 0,95 | 0,95 | ... | 0,95 | 0,95 |
| 0,95 | 1,10 | 1,12 | 1,12 | 1,12 | ... | 1,13 | 1,13 |
| 0,99 | 1,27 | 1,37 | 1,41 | 1,42 | ... | 1,49 | 1,4 |
Таблиця 2.3
Число cкладових, m | Значення коефіцієнта kq при співвідношенні границь | ||||||||
| 0 | 1/2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 2 | 0,98 | 1,15 | 1,27 | 1,22 | 1,15 | 1,12 | 1,08 | 1,07 | 1,05 |
| 3 | 1,27 | 1,32 | 1,37 | 1,32 | 1,24 | 1,18 | 1,15 | 1,12 | 1,08 |
| 4 | 1,38 | 1,40 | 1,41 | 1,36 | 1,28 | 1,23 | 1,18 | 1,15 | 1,11 |
Параметр ![]() , який характеризує співвідношення складових невилученої систематичної похибки, дорівнює найменшому із співвідношень границь
, який характеризує співвідношення складових невилученої систематичної похибки, дорівнює найменшому із співвідношень границь 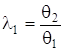 та
та 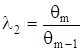 , при цьому
, при цьому ![]() .
.
При малому числі складових (![]() ) після знаходження статистичної границі qд необхідно порівняти її з арифметичною границею qа і прийняти як остаточну найменшу з двох границь. Слід зазначити, що для малого числа складових арифметичні границі qа звичайно незначно перевищують статистичні qд — не більше як на 30 %, що в багатьох випадках цілком припустимо.
) після знаходження статистичної границі qд необхідно порівняти її з арифметичною границею qа і прийняти як остаточну найменшу з двох границь. Слід зазначити, що для малого числа складових арифметичні границі qа звичайно незначно перевищують статистичні qд — не більше як на 30 %, що в багатьох випадках цілком припустимо.
Якщо невилучені систематичні складові похибки задані своїми довірчими границями ![]() , обчисленими за формулою (2.22), то довірчу границю сумарної систематичної похибки знаходять із виразу
, обчисленими за формулою (2.22), то довірчу границю сумарної систематичної похибки знаходять із виразу
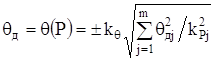 ,
,
де ![]() - довірчі границі j-ї невилученої систематичної складової похибки, що відповідають довірчій ймовірності
- довірчі границі j-ї невилученої систематичної складової похибки, що відповідають довірчій ймовірності ![]() ;
;
![]() - квантильний коефіцієнт переходу, що відповідає довірчій імовірності
- квантильний коефіцієнт переходу, що відповідає довірчій імовірності ![]() .
.
2.9.3. Визначення сумарної випадкової похибки вимірювань
В основу підсумовування випадкових складових похибки вимірювань покладена властивість дисперсії для суми залежних випадкових величин, яка стосовно похибок записується так:
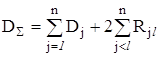 , (2.23)
, (2.23)
де ![]() - дисперсія суми n випадкових похибок;
- дисперсія суми n випадкових похибок;
![]() - дисперсія j-ї складової випадкової похибки,
- дисперсія j-ї складової випадкової похибки, ![]() ;
;
![]() - взаємна кореляційна функція, або взаємний кореляційний момент j‑ї та l-ї складових випадкової похибки, причому запис
- взаємна кореляційна функція, або взаємний кореляційний момент j‑ї та l-ї складових випадкової похибки, причому запис ![]() означає, що підсумовування розповсюджується на всі можливі попарні сполучення складових, для яких
означає, що підсумовування розповсюджується на всі можливі попарні сполучення складових, для яких ![]() . Взаємна кореляційна функція
. Взаємна кореляційна функція ![]() визначається рівнянням
визначається рівнянням
![]() , (2.24)
, (2.24)
де ![]() - відповідно СКВ (або їх оцінки
- відповідно СКВ (або їх оцінки ![]() ) j-ї та l-ї складових випадкової похибки:
) j-ї та l-ї складових випадкової похибки:
![]() ;
;
![]() - нормована взаємна кореляційна функція, або коефіцієнт кореляції:
- нормована взаємна кореляційна функція, або коефіцієнт кореляції:
![]() .
.
Переходячи у формулі (2.23) до СКВ випадкових похибок з урахуванням (2.24), одержимо вираз для обчислення СКВ сумарної випадкової похибки за її складовими
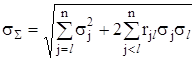 . (2.25)
. (2.25)
Звернемо увагу на те, що ця формула підсумовування випадкових похибок є універсальною, оскільки СКВ (і дисперсія) не залежить від закону розподілу похибок.
Відзначимо, що строго врахувати всі кореляційні зв’язки, а отже, і точно визначити коефіцієнт кореляції між похибками досить складно і не завжди можливо. Так, коефіцієнт кореляції між величинами ![]() визначається виразом
визначається виразом
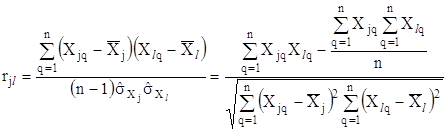 ,
,
де ![]() - результати q-го спостереження величин
- результати q-го спостереження величин ![]() ,
, ![]() відповідно,
відповідно, ![]() ;
;
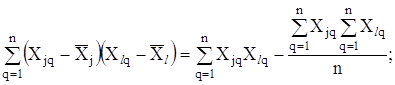
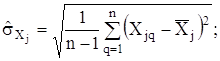
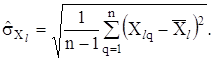
Застосування формули (2.25) потребує ускладнення експерименту і обчислювань. Тому вона не знаходить широкого практичного застосування, а для її спрощення користуються нижчевказаними рекомендаціями щодо задання коефіцієнта кореляції ![]()
За степенем корельованості випадкові похибки слід розділити лише на два види: сильно корельовані і слабко корельовані. Умовною границею між сильною і слабкою кореляціями випадкових похибок вважають умову ![]() . Враховуючи це, до сильно корельованих належать похибки, для яких
. Враховуючи це, до сильно корельованих належать похибки, для яких ![]() , і для них приймають
, і для них приймають ![]() . Прикладами сильно або жорстко корельованих похибок є похибки, викликані однаковою причиною (загальним джерелом живлення, майже однаковим впливом змінювання температури і т.п.), і в інших випадках, коли тісні кореляційні зв’язки між похибками явно проглядаються. До слабко корельованих належать похибки, для яких
. Прикладами сильно або жорстко корельованих похибок є похибки, викликані однаковою причиною (загальним джерелом живлення, майже однаковим впливом змінювання температури і т.п.), і в інших випадках, коли тісні кореляційні зв’язки між похибками явно проглядаються. До слабко корельованих належать похибки, для яких ![]() і для них приймають
і для них приймають ![]() . Такі похибки звичайно викликаються різними причинами, причому такими, що не мають між собою явного зв’язку. Вони також називаються незалежними. Проміжні значення коефіцієнта кореляції, тобто крім
. Такі похибки звичайно викликаються різними причинами, причому такими, що не мають між собою явного зв’язку. Вони також називаються незалежними. Проміжні значення коефіцієнта кореляції, тобто крім ![]() або
або ![]() , при оцінюванні випадкової похибки, як правило, не використовуються.
, при оцінюванні випадкової похибки, як правило, не використовуються.
У практиці вимірювань здебільшого мають справу з незалежними випадковими похибками, для яких ![]() і формула (2.25) набуває вигляду
і формула (2.25) набуває вигляду
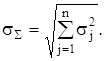 (2.26)
(2.26)
Якщо СКВ похибки ![]() визначити у відносних одиницях, то
визначити у відносних одиницях, то
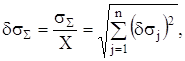 (2.27)
(2.27)
де ![]() - відносне СКВ j-ї складової похибки.
- відносне СКВ j-ї складової похибки.
Інколи для спрощення розрахунків переходять від підсумовування дисперсій (або СКВ) випадкових похибок до підсумовування максимальних (допустимих) значень абсолютних похибок ![]() . Тоді аналогічно формулам (2.22) і (2.26) маємо
. Тоді аналогічно формулам (2.22) і (2.26) маємо
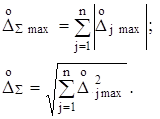 (2.28)
(2.28)
Формула для СКЗ сумарної випадкової похибки ![]() дає завищену оцінку в порівнянні з (2.26), але ця оцінка більш вірогідна, ніж "оцінка зверху"
дає завищену оцінку в порівнянні з (2.26), але ця оцінка більш вірогідна, ніж "оцінка зверху" ![]() .
.
Таким чином, арифметичне підсумовування використовується для грубої оцінки сумарної похибки, названої "оцінкою зверху" (або за максимумом), і при випадковому характері похибок. Воно зводиться до підсумовування максимальних значень окремих складових похибок. При такому підході передбачається, що всі складові випадкової похибки мають одночасно і максимальне значення, і однаковий знак. Очевидно, ймовірність такого збігу дуже мала, тому арифметичне підсумовування дає завищену оцінку сумарної випадкової похибки, і похибка цієї оцінки буде тим істотніша, чим більше число складових підсумовується. Тому арифметичне підсумовування випадкових похибок можливе при грубій оцінці сумарної похибки, коли вона містить 2-3 складових.
Переходячи в (2.28) до відносних похибок, маємо
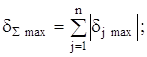
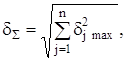
де ![]()
При умові ![]() формула (2.25) набуває вигляду
формула (2.25) набуває вигляду
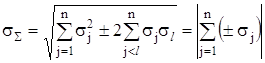 , (2.29)
, (2.29)
де знак "+" означає, що для складових з позитивною кореляцією (![]() ) СКВ
) СКВ ![]() треба брати зі знаком "+", а для складових з негативною кореляцією
треба брати зі знаком "+", а для складових з негативною кореляцією ![]() брати зі знаком "-". Знак модуля належить до
брати зі знаком "-". Знак модуля належить до ![]() .
.
Зокрема, при підсумовуванні двох складових випадкової похибки, СКВ яких ![]() , з (2.29) маємо
, з (2.29) маємо
![]() ,
,
тобто наявність жорсткої кореляції (![]() ) між випадковими складовими похибки приводить до переходу від геометричного їх підсумовування до алгебраїчного.
) між випадковими складовими похибки приводить до переходу від геометричного їх підсумовування до алгебраїчного.
Таким чином, при виборі того або іншого методу (правила) підсумовування складових похибки визначальною ознакою є не розділ їх на систематичні і випадкові, а ступінь (рівень) кореляційних зв’язків: сильний або слабкий.
Якщо для складових випадкової похибки задано границі довірчих інтервалів ![]() і довірчі ймовірності
і довірчі ймовірності ![]() , то СКВ кожної із складових, згідно з виразом (2.9), знаходять за формулою
, то СКВ кожної із складових, згідно з виразом (2.9), знаходять за формулою
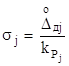 .
.
Якщо всі складові випадкової похибки підлягають однаковому закону розподілу і мають однакову довірчу ймовірність P, тоді ![]() і
і 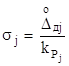 .
.
При нормальному законі розподілу всіх складових або при кількості складових n ³ 5 сумарна випадкова похибка має нормальний закон розподілу. Отже, її границі довірчого інтервалу з довірчою ймовірністю P можна визначити так: ![]() .
.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Влияние высоты установки антенны БС на уровень принимаемого сигнала
- Внешние запоминающие устройства
- Внешние запоминающие устройства(ВЗУ)
Реферативная работаВНЕШНИЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВАСодержаниеВведение. 3Внешние запоминающие устройства на гибких магнитных дисках. 4
- Внутренняя организация микроконтроллеров AVR
Внутренняя организация микроконтроллеров AVRМикроконтроллеры AVR выпускаются фирмой Atmel и предназначены для свободного использования в
- Воздействие радиационного излучения на операционные усилители
- Воздействия в электрических цепях
Воздействия в электрических цепяхКлассификация воздействий в электрических цепяхВоздействиями в электротехнике называют различные п
- Возможности биллинговых систем для операторов фиксированной связи
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

