Скачать

Взаимодействие бета-частиц с веществом

Курсовая работа на тему:

Взаимодействие бета-частиц с веществом

Для того чтобы уметь регистрировать ядерное излучение и для того чтобы уметь от него защищаться (если это нужно), необ­ходимо знать, за счет каких процессов теряет свою энергию части­ца, проходя через вещество; какова проникающая способность частиц; как зависят вероятности различных процессов взаимодей­ствия от параметров частицы (заряда, массы, энергии) и от свойств вещества (заряда ядер, плотности, ионизационного потен­циала).

Перечислим основные процессы взаимодействия заряженных частиц и Y-квантов с веществом (вопрос о взаимодействии нейтро­нов будет рассмотрен отдельно в главе, посвященной физике ней­тронов).

Взаимодействие заряженных частиц со средой.

1. Основной причиной потерь энергии заряженной частицей при прохождении через вещество являются столкновения ее с атомами этого веще­ства. Ввиду того, что масса ядра всегда велика по сравнению с массой электронов атома, можно достаточно четко провести раз­личие между «электронными столкновениями», при которых энер­гия падающей частицы передается одному из электронов атома, в результате чего происходит возбуждение или ионизация атома (неупругое столкновение), и «ядерными Столкновениями», при ко­торых импульс и кинетическая энергия частицы частично перехо­дят в поступательное движение атома как целого (упругое столк­новение). Повторяясь, эти ядерные столкновения приводят к многократному рассеянию частиц в веществе.

2. Существенную роль в потерях энергии легких заряженных частиц (электронов) играет также радиационное торможение. Сущность этого процесса заключается в том, что при рассеянии заряженной частицы кулоновским полем ядра или электрона эта частица получает ускорение, что в соответствии с законами электродинамики всегда приводит к электромагнитному излучению. Возникает непрерывный спектр -лучей — тормозное излучение.

3. В случае тяжелой частицы (протон, - частица и др.), когда ее энергия достаточно велика для преодоления кулоновского барье­ра ядра, может произойти также процесс потенциального рассея­ния на ядрах или же ядерная реакция, сопровождающаяся вылетом из ядра различных частиц, испусканием - квантов, делением ядра и др.

4. При движении заряженной частицы в среде со скоростью, превышающей фазовую скорость света в этой среде , где п — показатель преломления среды, возникает специфическое свечение, названное излучением Вавилова—Черенкова.

Взаимодействие -излучения со средой.

-лучи, проходя через вещество, теряют свою энергию главным образом за счет следую­щих явлений.

1. Комптон-эффект, или рассеяние - квантов на электронах, при котором фотоны передают часть своей энергии электронам атома.

2. Фотоэффект, или поглощение - кванта атомом, когда вся энергия фотона передается электрону, вылетающему в результате этого из атома.

3. Образование электрон-позитронных пар — процесс, который может происходить в поле ядра или другой частицы при энергиях -квантов

4. Ядерные реакции, возникающие обычно при энергиях -квантов, превышающих 10 МэВ.

Во многих физических экспериментах применяются пучки электронов, причем энергия электронов может быть самой раз­ной — от долей электронвольта до миллионов электронвольт. В ядерной физике используются как пучки электронов, полученные на ускорителе, так и пучки электронов, возникающих при бета-распаде радиоактивных ядер - "бета-частицы". В обоих случаях могут быть получены сведения о свойствах атомных ядер и стро­ении вещества. Знание энергии бета-излучения необходимо для многих научных и практических целей.

В отличие от альфа-частиц бета-частицы, испускаемые каким-либо радиоактивным веществом, имеют непрерывный, энергети­ческий спектр, в котором представлены бета-частицы, имеющие все значения кинетической энергии от нуля до некоторого макси­мального значения.

Бета-распадом называется самопроизвольное превращение атомного ядра, при котором его заряд (Z) меняется на единицу, а массовое число (А) остается неизменным.

Различают три вида бета-распада:

1. -распад, при котором из ядра испускается электрон и антинейтрино :

(1)

При - распаде , т. е. число протонов в ядре увеличи­вается на единицу, а число нейтронов уменьшается на единицу.

2. -распад, при котором из ядра испускается позитрон и нейтрино :

. (2)

-распад может происходить только в случае, если масса ис­ходного атома превышает массу конечного атома на величину . При -распаде.

3. Электронный захват, при котором один из электронов атом­ной оболочки (например, электрон К-оболочки) захватывается ядром и при этом испускается нейтрино :

(3)

Если энергия распада больше энергии связи К-электронов (са­мых близких к ядру), то происходит преимущественно К-захват. При электронном захвате .

Бета-процессы обусловлены слабым взаимодействием - одним из четырех видов известных фундаментальных взаимодействий. Однако вероятность бета-распада в отличие от "слабого" распада элементарных частиц, зависит от структуры ядра. Исследования бета-процессов привели к крупным открытиям в физике: обнаружению новой элементарной частицы — нейтрино и открытию несохранения четности при слабых взаимодействиях. Экспери­ментальное изучение бета-распада приносит много новых данных о структуре ядер.

При - и -распаде из ядра испускаются две частицы. В каждом единичном акте распада энергия перехода делится меж­ду бета-частицей и нейтрино (энергией отдачи ядра можно прене­бречь), так что кинетическая энергия электрона (или позитрона) может принимать любые значения от нуля до максимально воз­можной величины . При электронном захвате энергия делится только между нейтрино и ядром отдачи, при этом нейтрино уно­сит практически всю энергию распада. Для большого количества одинаковых ядер в результате статистического усреднения полу­чается вполне определенное распределение электронов (позитро­нов) по энергиям. Это распределение называется бета-спектром, а величина - граничной энергией бета-спектра. Значения для бета-распада для различных радиоактивных веществ могут сильно различаться. Например, радиоактивный нуклид (три­тий) испускает бета-частицы с =18,60 кэВ, в случае же граничная энергия спектра равна 16,6 МэВ. Большая часть зна­чений лежит в интервале 10—5000 кэВ. Максимальная энер­гия бета-частиц определяет энергию распада и является важной физической величиной.

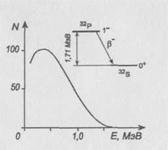
Рис. 1. Бета-спектр и схема распада ³²Р

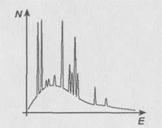
Рис. 2. Бета-спектр с линиями электронов внутренней конверсии

Типичный бета-спектр показан на рис. 1. Бета-распад ³²Р происходит на основное состояние ³²S и не сопровождается -излучением (см. схему распада). Во многих случаях бета-распад происходит на возбужденные уровни ядра-продукта. В этих слу­чаях бета-и:злучение сопровождается -излучением.При этом возбужденное ядро может передать энергию электронам атомных оболочек, в результате чего образуются моноэнергетические группы электронов с энергией , где hv— энер­гия -излучения, Е_св— энергия связи на одной из атомных обо­лочек. Это явление называется эффектом внутренней конвер­сии -излучения. Электроны внутренней конверсии могут затруд­нять измерения бета-спектров. Участок бета-спектра с линиями электронов внутренней конверсии при распаде показан на рис. 2.

Взаимодействие электронов с веществом

Электроны, движущиеся в веществе, взаимодействуют с его атомами, в результате чего теряют свою энергию и отклоняются от первоначального направления, т. е. рассеиваются. Рассеяние называется упругим, если сохраняется сумма кинетических энер­гий взаимодействующих частиц. Всякое иное рассеяние называ­ется неупругим. Следует различать взаимодействие электронов с атомными электронами и атомными ядрами, хотя оба вида взаи­модействия всегда происходят одновременно.

Взаимодействие -частиц с атомными электронами приводит к передаче атомному электрону некоторой энергии, следствием чего является либо ионизация, либо возбуждение ато­ма. Оба вида передачи энергии имеют примерно равную вероят­ность и объединяются под общим названием "ионизационные по­тери энергии". Теория ионизационных потерь электронов была разработана Бором, а также Бете и Блохом, которые получили формулу для потери энергии на ионизацию на единице пути

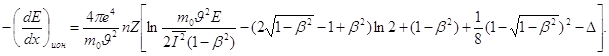
(4)

где и Е — скорость и кинетическая энергия падающего элек­трона; и е масса покоя и заряд электрона; Zзаряд ядра; п — число атомов в 1 см³ среды (, где А — атомный номер вещества); — средняя энергия возбуждения атома; — член, учитывающий поляризацию среды.

Л. Д. Ландау показал, что средние потери энергии моно­хроматическими электронами при прохождении слоя вещества с атомным номером А и зарядовым числом Zсоставляют:

(5)

где — плотность вещества, г/см³, — толщина слоя вещества, см.

Так как отношение Z/Aдля разных веществ приблизительно постоянно, то величина (dE/dx) в формуле (5.5) практически за­висит лишь от плотности вещества . Очень слабая зависимость от Zпроявляется только в средней энергии возбуждения , ко­торая стоит под знаком логарифма. Следовательно, пробег элек­тронов с данной первоначальной энергией Е в различных веще­ствах с одинаковой плотностью будет приблизительно одинако­вым. Поэтому за меру толщины вещества, взаимодействующего с электронами, берут произведение линейной толщины и плотности вещества и выражают пробег в единицах г /см²или мг/см².

При взаимодействии-частиц с ядрами происходят процессы упругого рассеяния электронов в кулоновском поле яд­ра и неупругого рассеяния, сопровождаемого испусканием элек­тромагнитного излучения.

Упругое рассеяние электронов в кулоновском поле ядра мо­жет быть условно разделено на четыре класса: однократное рас­сеяние, кратное рассеяние, многократное рассеяние и диффузия. Если толщина слоя мала, , где — эффективное сечение процесса), то происходит только однократное рассеяние, т. е. почти все рассеяние обусловлено только одним ядром. Для больших толщин ()получается кратное рассеяние, т. е. угол рассеяния обязан нескольким последовательным однократ­ным актам рассеяния. При многократном рассеянии (среднее чис­ло актов рассеяния больше 20) угловое распределение рассеян­ных электронов является приблизительно гауссовым до тех пор, пока средний угол рассеяния меньше 20°. Для еще больших тол­щин ()угловое распределение рассеянных электронов принимает вид . Средний угол рассеяния дости­гает максимальной величины =33° и остается постоянным при дальнейшем увеличении толщины. Это случай полной диффузии. Электроны выходят из слоя также и со стороны падающего пучка— это так называемое обратное рассеяние электронов.

Неупругие процессы при взаимодействии электрона с ядром связаны с испусканием электромагнитного излучения, возникаю­щего при ускорении электрона в кулоновском поле ядра. Рожден­ное в таком процессе -излучение является тормозным. Потеря энергии электрона на тормозное излучение называется радиаци­онной. Согласно Гейтлеру радиационные потери на единице дли­ны равны

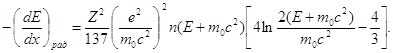(6)

Вероятность образования тормозного излучения пропорцио­нальна квадрату заряда ядра, поэтому радиационные потери энергии играет большую роль в тяжелых элементах. Излучение является важным механизмом потери энергии электронами, но этот механизм несущественен для более тяжелых частиц (мезо­нов, протонов и др.).

Сравнение формул для потерь энергии на излучение и на ионизацию показывает, что потери энергии имеет разный ха­рактер. Так, потери энергии на излучение пропорциональны Z² и увеличиваются с энергией линейно, в то время как потери на ионизацию пропорциональны Zи увеличиваются с энергией лишь логарифмически. Поэтому при больших энергиях падаю­щих электронов преобладают потери на излучение. С уменьше­нием энергии электрона роль ионизации (и возбуждения) увели­чивается. При энергии (МэВ) оба вида потери энер­гии имеют примерно равную вероятность. Отметим, что для А1 (Z—13) — 46 МэВ. Для электронов, испускаемых при радио­активном распаде, радиационные потери в общем балансе поте­ри играют незначительную роль, так как значения энергии бета-распада обычно не превышают 5 МэВ.

Все сказанное выше применимо и для позитронов. Надо за­метить, что проникающая способность позитронов немного отли­чается от проникающей способности электронов той же энергии ввиду того, что позитроны и электроны несколько по-разному рассеивается в поле ядра. Вызванное этим обстоятельством раз­личие в поведении данных частиц не является существенным.

Детектирование.

Основным принципом детектирования электронов является регистрация ионов, образующихся в результате взаимодействия электронов с веществом детектора. К таким детекторам относят­ся газонаполненные и твердотельные детекторы.

Так как число нар ионов, создаваемых при движении элек­тронов в веществе детектора, сравнительно невелико, то более эффективными газонаполненными детекторами являются счет­чики с газовым усилением (счетчики Гейгера-Мюллера и про­порциональные счетчики). Большой эффективностью обладают и твердотельные детекторы (сцинтилляторы и полупроводники). Например, при толщине детектирующего слоя 10 мм полупро­водниковые детекторы регистрируют почти со стопроцентной ве­роятностью бета-частицы с энергией до 3 МэВ.

Достоинством пропорциональных счетчиков, сцинтилляционных и полупроводниковых детекторов является возможность по­лучать от этих приборов электрические импульсы, амплитуда ко­торых пропорциональна энергии бета-частицы. Это обстоятель­ство позволяет регистрировать спектры бета-частиц. Из перечис­ленных выше приборов наилучшими спектральными характеристиками обладают полупроводниковые детекторы, на которых по­лучают электронные линии с полушириной ~1 кэВ. Более высо­кой разрешающей способностью (до 1—10 эВ) обладают электро­статические и магнитные спектрометры, но эти приборы весьма сложны, дороги и, как правило, обладают малой светосилой (т.е. регистрируют лишь незначительную часть электронов, испущенных источником). В тех опытах, в которых не требуется знание спектрального распределения электронов, для их регистрации ис­пользуются счетчики Гейгера-Мюллера как наиболее простые и эффективные детекторы. Для измерения спектрального распре­деления бета-частиц используются сцинтилляционные кристаллы и полупроводниковые детекторы. Из других методов детектиро­вания электронов отметим счетчики, регистрирующие черенковское свечение, возникающее при прохождении быстрых электро­нов через вещество, однако эти счетчики наиболее эффективны при больших энергиях электронов.

Определение граничной энергии бета-спектра методом поглощения

Знание максимальной энергии бета-излучения необходимо для решения многих научных и практических задач. Во многих важ­ных случаях периоды полураспада оказываются очень коротки­ми и составляют всего несколько минут или даже секунд. При этом часто приходится иметь дело с препаратами малой интен­сивности. Поэтому необходимы простые и быстрые способы опре­деления максимальной энергии бета-излучения, не требующие к тому же больших активностей. Одним из таких способов являет­ся метод поглощения, которым можно определить максимальную энергию бета-спектра с погрешностью порядка 5—10%. Такая точ­ность часто бывает достаточной при решении прикладных задач. Точнее определить энергию бета-частиц можно с помощью про­порционального счетчика, сцинтилляционного, полупроводнико­вого и магнитного спектрометров.

Принцип метода поглощения заключается в определении про­бега электронов в каком-либо веществе.

Рассмотрим пучок электронов, падающий нормально на по­верхность фильтра (рис. 29). Первоначально быстрые электроны проходят в поглотителе некоторое расстояние приблизительно по прямой линии, теряя небольшие количества энергии и испыты­вая лишь малые отклонения.

По мере уменьшения энер­гий электронов их рассеяние становится более 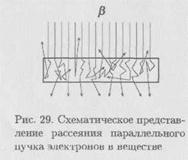сильным. Уг­ловое распределение электро­нов в пучке начинает прибли­жаться к гауссову, характерно­му для многократного рассея­ния. В этой области наиболее ве­роятный угол рассеяния увели­чивается пропорционально квадратному корню из пройденной толщины фольги. При дальнейшем рассеянии угловое распреде­ление становится настолько размытым, что нельзя говорить о каком-либо преимущественном направлении движения электро­нов, и их распространение можно рассматривать как диффузию.

Число электронов, прошедших через фольгу, есть монотонно убывающая функция толщины фольги. Для умеренных толщин уменьшение числа электронов является следствием, главным об­разом, обратной диффузии электронов, которые отклоняются на углы, превышающие 90°, в результате сложения большого числа отклонений на малые углы. При дальнейшем увеличении толщи­ны фольги уменьшение числа электронов происходит как вслед­ствие рассеяния, так и по причине того, что часть из них тормо­зится практически до нулевой энергии и, таких образом, выбы­вает из пучка. Предельная толщина фольги, практически полно­стью задерживающая первоначально падающие электроны, на­зывается эффективным пробегом электронов. Этот пробег опре­деляется по кривым поглощения.

Так как теоретические расчеты эффективного пробега моно­энергетических электронов в конденсированной среде трудны, приходится обращаться к установлению эмпирического соотно­шения "пробег — энергия" путем измерения пробега моноэнергетических электронов известной энергии.

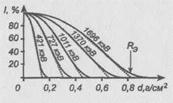
Рис. 4. Кривые поглощения моноэнергетических электронов разных энергий в алюминии.

Однако при этом возникает трудность экспериментально­го определения пробега по измеренной кривой поглощения. Экспериментально пробег не может быть определен как пре­дельная толщина поглотителя, которую уже не могут пройти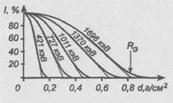 первоначально падающие элек­троны, так как различные элек­троны данного пучка рассе­иваются или тормозятся по-разному и такая толщина прак­тически не существует.

На рис. 5 приведены типич­ные кривые поглощения в алю­минии для моноэнергетических электронов различных энергий. По оси абсцисс отложена толщина dалюминиевого фильтра, по оси ординат — интенсивность Iпучка электронов, прошедших через фильтр. Каждая кривая имеет после начальной выпуклой части довольно длинную прямо­линейную часть, заканчивающуюся некоторым "хвостом". Наи­более воспроизводимой чертой кривых поглощения, снятых при различных условиях эксперимента является точка пересечения линейной части кривой поглощения с осью абсцисс (экстраполи­рованный пробег,).

Экстраполированный пробег используется для практических целей. Выше 0,8 МэВ связь между пробегом и энерги­ей электронов может быть выражена линейным соотношением = А + BE, где А и В — константы.

Кривые поглощения в случае бета-излучения, имеющего непрерывный энергетический спектр, отличаются от кривых по­глощения для моноэнергетических электронов более резким, по­чти экспоненциальным спадом. Такой спад объясняется тем, что в пучке бета-частиц имеются электроны всевозможных энергий, в том числе и очень малых, медленные же электроны поглощают­ся весьма сильно. Типичная кривая поглощения бета-излучения приведена на рис. 5а. Как видно, конец кривой поглощения под­ходит к линии фона асимптотически. Такой ход кривой объясня­ется постепенно уменьшающимся в бета-спектре числом быстрых электронов и относительно слабым поглощением электронов мак­симальной энергии. По такой кривой поглощения нельзя произ­вести непосредственное определение пробега.

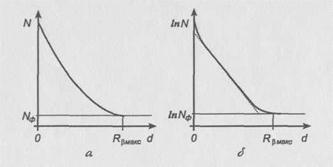
Рис. 5. Типичная кривая поглощения для случая непрерывного бета-спектра (а), (б) – та же кривая в полулогарифмическом масштабе

Для определения пробега целесообразно построить рассматри­ваемую кривую в полулогарифмическом масштабе (рис. 5б). В этом случае пробег бета-частиц, соответствующий их максимальной энергии, определяется по точке пересечения конца кривой поглощения с линией фона.

Для определения максимальной энергии бета-излучения необ­ходимо иметь кривую "пробег—энергия", такую же, как в слу­чае моноэнергетических электронов. Многие исследователи зани­мались установлением зависимости между максимальным пробегом .

Некоторые простые эмпирические соотношения между энер­гией и максимальным пробегом бета-частиц в алюминии даются уравнениями

Е = 1,39 R^0,6, при Е< 0,15 МэВ, (7)

Е = 1,92 R^0,725, при 0,15 МэВ< Е< 0,8 МэВ. (8)
Е = 1,85 R + 0,245, при Е> 0,8 МэВ. (9)

В формулах (5.7) (5.9) максимальный пробег Rдан в грам­мах на квадратный сантиметр (г/см²) алюминиевого фильтра, способного практически полностью поглотить бета-частицы с данной граничной энергией.

На рис.42-43 приведена кривая, связывающая пробег бета-частиц с их максимальной энергией.

Непрерывное энергетическое распределение бета-частиц, ис­пускаемых радиоактивными веществами, и рассеяние электронов при прохождении через вещество приводит к тому, что ослабле­ние пучка бета-частиц, идущих от источника к детектору, носит характер, близкий к экспоненциальному закону

(10)

где d — толщина фильтра; 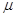— коэффициент ослабления.

Экспоненциальный закон хорошо совпадает с эксперименталь­ной кривой в области средних значений толщины поглотителя. В области малых и больших значений наблюдается заметное от­ступление от экспоненциального закона (см. рис. 5б.) При изме­рениях удобно пользоваться толщиной слоя половинного погло­щения, необходимого для уменьшения вдвое начальной ин­тенсивности бета-излучения. Так как и, то

(11)

Коэффициент ослабления находят по наклону прямолинейно­го участка кривой поглощения , где угол наклона прямой).

Связь между толщиной слоя алюминия, ослабляющего из­лучение в раз, и верхней границей бета-спектра была тща­тельно исследована. На с. 94 приводится номограмма, связываю­щая толщину слоя половинного поглощения с граничной энергией — спектра.

Обратное рассеяние электронов

При попадании потока электронов на поверхность какого-либо материала часть частиц может отклониться от своего первона­чального направления на угол, превышающий 90°. Этот эффект называется обратным рассеянием электронов. Обратное рассея­ние электронов используется для решения ряда прикладных за­дач, например для определения толщины покрытий. Этот же эф­фект может быть и источником методических погрешностей. Его следует учитывать при проведении физических экспериментов с электронными пучками. Например, при вылете бета-частиц из радиоактивного источника распределение бета-частиц искажает­ся из-за их рассеяния в материале подложки, в результате че­го увеличивается число частиц, вылетающих в сторону счетчика и, следовательно, увеличивается скорость счета. Другой пример:

при измерении бета-спектров полупроводниковыми или сцинтилляционными детекторами из-за эффекта обратного рассеяния на поверхности детектора происходит обогащение низкоэнергетиче­ской части спектра.

Коэффициент обратного рассеяния

Введем величину, характеризующую явление обратного рас­сеяния коэффициент обратного рассеяния

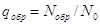(12)

где 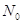— число частиц, падающих нормально на поверхность ма­териала; 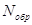— число частиц, рассеянных материалом на угол 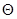>90°. Коэффициент обратного рассеяния является функцией атомного номера Z отражателя, толщины отражателя d и энер­гии падающих электронов Е (а в случае непрерывного спектра бета-частиц — функцией максимальной энергии Е_макс), т. е.

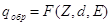(13)

На рис. 32 приведена типичная экспериментальная зависи­мость q(Z) в случае отражения бета-частиц, испущенных радио­активным препаратом ³²Р. Толщины материалов взяты заведомо больше, чем толщины обратного насыщения (см. далее).

Экспериментальная кривая, показанная на рис. 32, удовлетво­ряет аналитической зависимости 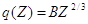, где В — коэф­фициент, зависящий от геометрических условий опыта, в част­ности от телесного угла окна счетчика. Здесь следует отметить, что обратно рассеянное излучение неизотропно — его максималь­ная интенсивность наблюдается в направлении, перпендикуляр­ном плоскости отражателя. Максимальная энергия и максималь­ный пробег отраженных электронов также зависит от Z. Напри­мер, в случае излучателя ³²Р

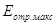= 0,247 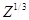МэВ ,

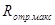= 48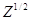 мг/см² .

Если увеличивать толщину отражателя и измерять интенсив­ность потока обратно рассеянных электронов, то сначала q будет возрастать почти линейно (рис. 33). затем рост замедлится и да­лее достигнет некоторого предельного значения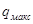

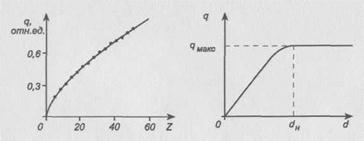
Рис. 6. Зависимость коэффи­циента обратного рассеяния qот атомного номера 2 отражателя

Рис. 7. Зависимость коэффи­циента обратного рассеяния от толщины отражателя

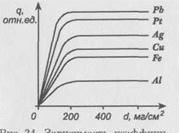
Рис. 8. Зависимость коэффициента обратного рассеяния от толщины отражателя из различных металлов. Излучатель

Толщина слоя вещества, на­чиная с которой qне зависит от толщины отражателя, на­зывается толщиной насыщения обратного рассеяния d_H.Эта толщина равна примерно 1/5 от максимального пробега бета-частиц данной энергии в данном веществе. Величина q зависит от атомного номера Zи слабо зависит от плотности электронов в веществе. Из рис. 8 видно, что меньше , хотя плотность электронов в платине больше, чем в свинце. Это свидетельствует о том, что рассеяние происходит в основном на атомных ядрах, а не на электронных оболочках атомов.

На рис. 10 схематически изображено обратное рассеяние бета-частиц при разных толщинах рассеивателя. Следует отметить, что обратное рассеяние бета-частиц в отличие от оптического от­ражения происходит не только на поверхности рассеивателя, но и в его глубине. На схеме действительная картина обратного рассе­яния сильно упрощена: показано рассеяние на один и тот же угол и не учтено поглощение бета-частиц веществом.

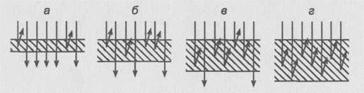
Рис. 10. Отражение бета-частиц в зависимости от толщины образца

При небольшой толщине рассеивателя большинство электронов про­ходит сквозь вещество, и лишь небольшое их число рассеивается в обратном направлении. По мере увеличения толщины число об­ратно рассеянных электронов увеличивается (б, в). Наконец, при d> d_Hчастицы, глубоко проникшие в рассеиватель, уже не вый­дут наружу из-за поглощения в нем (г). При дальнейшем увели­чении толщины рассеивателя число вышедших из него обратно рассеянных электронов остается постоянным.

Коэффициент обратного рассеяния растет с ростом гранич­ной энергии бета-спектра до энергии 0,6 МэВ, а далее остается практически неизменным. Зависимость коэффициента обратного рассеяния qот максимальной энергии показана на рис. 11.

Явление обратного рассеяния электронов может быть исполь­зовано для решения многих прикладных задач:

а) Для определения толщины материалов. В этом случае вы­годнее применять источники мягкого бета-излучения. Зависи­мость коэффициента обратного рассеяния от толщины алюминие­вого отражателя для разных бета-источников показана на рис. 12.

б) Для определения толщины покрытий. Эффект обратного рассеяния позволяет измерять толщины покрытия без разруше­ния изделий и покрытий. Не разрушает изделие микрометриче­ский метод, но он требует жесткого постоянства толщины основания, а также магнитный, но в этом случае покрытие должно об­ладать магнитными свойствами. Оптическими методами можно определить толщины только прозрачных покрытий. Химический метод связан с разрушением изделия и его точность не превы­шает 15%. В случае применения эффекта обратного рассеяния атомные номера вещества покрытия и подложки должны различаться, по крайней мере, на две единицы.

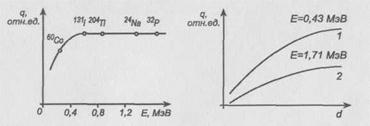
Рис.11. Зависимость коэффициента обратного рассеяния от максимальной энергии бета-спектра

Эффект обратного рассеяния позволяет измерять толщины никелевых и хромовых покрытий, покрытий на проволоке и бу­маге, светочувствительных слоев и т. д., составов на пленке, лако­вых покрытий на металлах, покрытий из драгоценных металлов. При этом все измерения делают бесконтактно, без разрушения изделий и непрерывно.

Обратно-рассеянное бета-излучение чувствительно к соста­ву раствора ионов с высокими атомными номерами (рис. 12). Возможно измерение концентрации одного металла в сплаве с другим. Здесь также необходимо иметь набор эталонов с раз­личной концентрацией компонентов. Поток обратно-рассеянных бета-частиц от смеси веществ и равен

(14)

где и — весовые концентрации компонентов, +=1.

ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ

Ионизационное торможение заряженных частиц. При электро­магнитном взаимодействии быстрых заряженных частиц с элект­ронами вещества последние переходят в возбужденное состояние; когда они остаются внутри атома, происходит возбуждение атома, и спектрэтих состояний имеет дискретный характер; в тех слу­чаях, когда электроны вырываются из атома, их энергия может иметь любые значения, а атом при этом ионизуется. Увеличение энергии электрона происходит за счет кинетической энергии па­дающей частицы. В обоих случаях для краткости принято гово­рить, что энергия летящей частицы убывает вследствие ионизаци­онных потерь.

Рассмотрим взаимодействие тяжелой заряженной частицы с электроном. Такая частица ничтожно отклоняется со своего прямо­линейного пути и этим отклонением можно пренебречь. Допустим, что частица с зарядом Ze, массой М и скоростью vпролетает на расстоянии от электрона, где — прицельный параметр, или па­раметр удара (рис. 13). Взаимодействие частицы с электроном приведет к тому, что электрон получит импульс в направлении, перпендикулярном к линии полета частицы

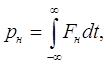
где F – электростатическая сила и - ее составляющая нормальная к линии полета, а t – время полета