Скачать

Аффинные преобразования

Глава I.Понятие о геометрическом преобразовании

1.1 Что такое геометрическое преобразование?

Осевая симметрия, центральная симметрия, поворот, параллельный перенос, гомотетия имеют то общее, что все они „преобразуют" каждую фигуру F в некоторую новую фигуру F1. Поэтому их называют геометрическими преобразованиями.

 Вообще, геометрическим преобразованием называют всякое правило, позволяющее для каждой точки А на плоскости указать новую точку A', в которую переводится точка А рассматриваемым преобразованием. Если на плоскости задана какая-либо фигура F, то множество всех точек, в которые переходят тонки фигуры F при рассматриваемом преобразовании, представляет собой новую фигуру F., В этом случае говорят, что F' получается из F при помощи рассматриваемого преобразования.

Пример. Симметрия относительно прямой l является геометрическим преобразованием. Правило, позволяющее по точке A найти соответствующую ей точку А', в этом случае заключается в следующем: из точки А опускается перпендикуляр АР на прямую l и на его продолжении за точку Р откладывается отрезок РА'=АР.

Сложение геометрических преобразований

Предположим, что мы рассматриваем два геометрических преобразования, одно из которых называем „первым", а другое - „вторым". Возьмем на плоскости произвольную точку А и обозначим через А' ту точку, в которую переходит А при первом преобразовании. В свою очередь точка А' переводится вторым преобразованием в некоторую новую точку А". Иначе говоря, точка А" получается из точки А при помощи последовательного применения двух преобразований - сначала первого, а затем второго.

Результат последовательного выполнения взятых двух преобразований также представляет собой геометрическое преобразование: оно переводит точку А в точку А". Это „результирующее" преобразование называется суммой первого и второго рассмотренных преобразований.

Пусть на плоскости задана какая-либо фигура F. Первое преобразование переводит ее в некоторую фигуру F' . Вторым преобразованием эта фигура F' переводится в некоторую новую фигуру F''. Сумма же первого и второго преобразований сразу переводит фигуру F в фигуру F".

Пример. Пусть первое преобразование представляет собой симметрию относительно точки О1 а второе преобразование - симметрию относительно другой точки О2. Найдем сумму этих двух преобразований.

Пусть А — произвольная точка плоскости. Предположим сначала, что точка A не лежит на прямой O1O2. Обозначим через А' точку, симметричную точке А относительно О1, а через A" — точку, симметричную точке A' относительно О2 . Так как О1O2 — средняя линия треугольника АА'А'' то отрезок АА" параллелен отрезку О1O2 и имеет вдвое большую длину. Направление от точки А к точке А" совпадает с направлением от точки

О1 к точке О2. Обозначим теперь через МN такой вектор, что отрезки MN и O1 O2 параллельны, отрезок МN в два раза длиннее отрезка O1О2 и лучи МN и O1O2 имеют одно и то же направление. Тогда АА" = МN, т. е. точка А" получается из точки А параллельным переносом на вектор МN.

То же справедливо и для точки, лежащей на прямой O1О2.

Окончательно мы получаем: сумма симметрии относительно точки O1 и симметрии относительно точки O2 представляет собой параллельный, перенос.

1.2 Движения

Осевая симметрия, поворот (в частности, центральная симметрия) и параллельный перенос имеют то общее, что каждое из этих преобразований переводит любую фигуру F на плоскости в равную ей фигуру F' . Преобразования, обладающие этим свойством, называются движениями. Гомотетия представляет собой пример преобразования, не являющегося движением. Действительно, каждое движение переводит любую фигуру в равную ей фигуру, т. е. изменяет лишь положение фигур на плоскости; гомотетия же изменяет и размеры фигур.

Роль движений в геометрии

Движения играют в геометрии чрезвычайно важную роль. Они не изменяют ни формы, ни размеров фигур, меняя лишь расположение фигуры. Но фигуры, отличающиеся лишь своим расположением на плоскости, с точки зрения геометрии совершенно одинаковы. Именно поэтому их и называют в геометрии «равными фигурами». Ни одно свойство геометрической фигуры не отличается от соответствующего свойства равной ей фигуры. Так, например, равные треугольники имеют не только одинаковые стороны, но и одинаковые углы, медианы, биссектрисы, площади, радиусы вписанной и описанной окружностей и так далее.

На уроках геометрии мы всегда считали равные фигуры (т. е. такие, которые можно совместить при помощи движения) одинаковыми или неразличимыми. Такие фигуры часто принимают за одну и ту же фигуру. Именно поэтому мы можем сказать, что, например, задача построения треугольника по двум сторонам а, b и заключенному между ними углу С имеет только одно решение. На самом деле, конечно, треугольников, имеющих данные стороны а и b и заключенный между ними угол С данной величины, можно найти бесконечно много. Однако все эти треугольники одинаковы, равны, поэтому их можно принять за «один» треугольник.

Таким образом, геометрия изучает те свойства фигур, которые одинаковы у равных фигур. Такие свойства можно назвать «геометрическими свойствами». Другими словами: геометрия изучает свойства фигур, не зависящие от их расположения. Но фигуры, отличающиеся только расположением (равные фигуры), — это те, которые можно совместить с помощью движения. Поэтому мы приходим к следующему определению предмета геометрии; геометрия изучает те свойства фигур, которые сохраняются при движениях.

Движения в геометрии и физике

Итак, понятие движения играет в геометрии первостепенную роль. Движения («наложения») использовались в VI классе для определения равных фигур, для доказательства признаков равенства треугольников; понятие движения, как мы видели выше, позволяет также дать описание предмета геометрии.

Между тем в определениях понятия равенства фигур и понятия движения имеется пробел. В самом деле, равные фигуры определялись (в VI классе) как такие фигуры, которые могут быть совмещены наложением (т. е. движением). Движения же были определены выше как такие преобразования, которые переводят два многоугольника F1 и F таковы, что существует многоугольник F', гомотетичный F и равный F1 , то углы многоугольника F соответственно равны углам многоугольника F' и стороны многоугольника F соответственно, пропорциональны сторонам многоугольника F'. Но у многоугольника F те же самые углы и стороны, что и у равного ему многоугольника F1. Следовательно, многоугольники F1 и F подобны в том смысле, в каком это понималось в курсе геометрии VIII класса.

Обратно, пусть многоугольники F1 и F таковы, что их углы соответственно равны и стороны соответственно пропорциональны. Отношение сторон многоугольника F1 к соответствующим сторонам многоугольника F обозначим через k. Далее, обозначим через F' многоугольник, получающийся из F гомотетией с коэффициентом k (и каким угодно центром гомотетии. В таком случае в силу теоремы многоугольники F' и F1 будут иметь соответственно равные стороны и углы, т. е. эти многоугольники будут равны. Поэтому многоугольники F1 и F будут подобны и в смысле приведенного здесь определения подобия.

Глава II.Аффинные преобразования

2.1 Аффинные преобразования плоскости

Аффинным преобразованием α называется такое преобразование плоскости, которое всякую прямую переводит в прямую и сохраняет отношение, в котором точка делит отрезок.

На рис.1: L'= α(L), A'=α(A), B'=α(B), C'=α(C), |

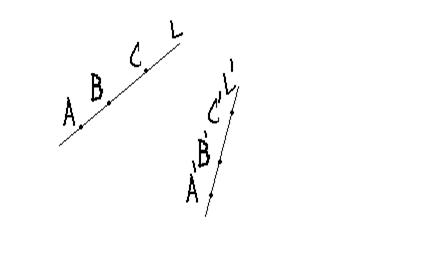
рис. 1

Преобразования - движение и подобие - являются частными случаями аффинных, так как в силу свойств движения и подобия для них выполнены все требования определения аффинных преобразований.

Приведем пример аффинного преобразования, не сводящегося к ранее рассмотренным. С этой целью сначала рассмотрим параллельное проектирование плоскости на плоскость.

Пусть даны плоскости: w и w1 прямая l (направление проектирования), не параллельная ни одной из этих плоскостей (рис.2). Точка Аєw называется проекцией точки А1єw1, если АА1||l , то прямая АА1 называется проектирующей прямой. Параллельное проектирование представляет собой отображение плоскости w1 на w.

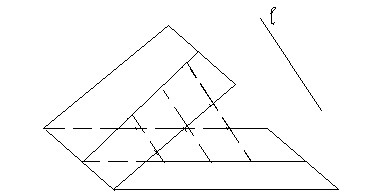
рис.2

Отметим следующие свойства параллельного проектирования.

1) Образом всякой прямой а1 является прямая.

В самом деле, прямые, проектирующие точки прямой а1, образуют плоскость (она проходит через а1 параллельно l), которая при пересечении с w дает образ прямой а1 – прямую а(рис.2).

2) Отношение, в котором точка делит отрезок, сохраняется, т.е.

 (рис.2)

Сразу следует из теоремы о пересечении сторон угла параллельными прямыми.

Перейдем непосредственно к построению примера аффинного преобразования.

Возьмем два экземпляра плоскости w и один из них переместим в другое положение w1(рис.3). Новое положение какой-либо точки Аєw обозначим А1єw1. Теперь плоскость w1 спроектируем в каком-нибудь положении на w, проекцию точки А1 обозначим А'.

Получилось преобразование плоскости w на себя, при котором . В силу симметричных свойств параллельного проектирования для данного преобразования выполняются оба требования определенного аффинного преобразования, следовательно, построенное сейчас преобразование –перспективно- аффинное.

рис.3

3)Основная теорема. Каковы бы ни были 2 аффинных репера  и , существует единственное аффинное преобразование, которое первый переводит во второй.

Существование. Рассмотрим преобразование а, которое произвольную точку А, имеющую в репере R координаты (х,у), переводит в точку А', имеющую в репере R' те же координаты (рис.4). Очевидно, что а(R)=R'. Покажем, что а - аффинное преобразование.

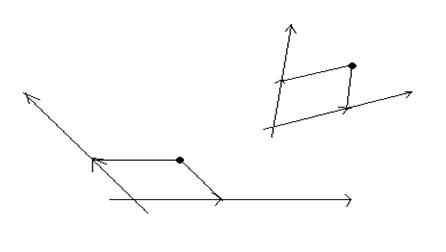
рис. 4

Образом прямой l, имеющей в репере R уравнение ах+ву+с=0, будет линия l', которая в R' имеет то же самое уравнение. Значит, l'- прямая(рис.5). Следовательно, образом произвольной прямой является прямая.

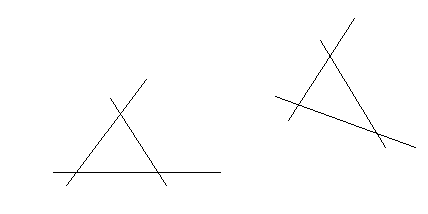
рис. 5

Пусть теперь точка С(х,у) делит отрезок, соединяющий точки А(х1,у1), В(х2,у2) в отношении

А так как образы этих точек- А',В',С' имеют те же координаты(в другой системе), то  и, следовательно,

Итак для преобразования α выполнены оба требования определения, значит α- аффинное преобразование.

Единственность доказательства от противного. Пусть существует два аффинных преобразования α1 и α2, при которых . Тогда найдется такая точка А, что , где (рис.6). Обозначим через К точку пересечения прямых ОА и Е1Е2(если эти прямые параллельны, то надо взять Е1А, ОЕ2, если и эти прямые параллельны, надо взять Е2А и ОЕ1). Так как , то образом точки К будет точка К'1-точка пересечения прямых . В силу определения аффинного преобразования:

Аналогично для преобразования α2.

Таким образом

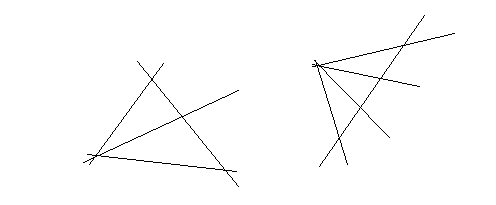
рис. 6

Первое из этих равенств показывает, что точки К'1 и К'2 совпадают, а тогда из второго следует А'1=А'2, что противоречит А. Полученное противоречие доказывает теорему.

Основную теорему можно сформулировать иначе: каковы бы ни были два треугольника, существует единственное аффинное преобразование, переводящее один в другой.

Доказанная основная теорема делает понятие аффинного преобразования конструктивным. Аффинное преобразование задается парой произвольных аффинных реперов.

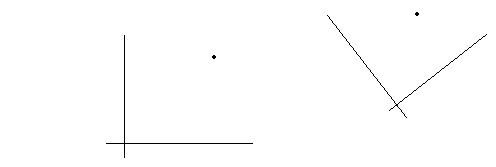
4)Уравнения аффинного преобразования получаются из основной теоремы и формул преобразования аффинных координат точно так же, как и уравнения движения и подобия. Пусть даны два репера  и (рис. 7).

рис. 7

O'(c1,c2),

OM'=OO'+O'M'

получаются уравнения:

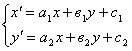
Эти уравнения записаны в аффинной системе координат. В частности они действуют и в прямоугольных декартовых координатах.

2.2 Свойства аффинного преобразования

1. Образом параллельных прямых являются параллельные прямые.

Доказательство от противного. Предположим, что образом параллельных прямых l и m являются пересекающиеся в точке А' прямые l' и m'(рис.8). В силу взаимной однозначности преобразования точка имеет прообраз, который обозначим А. Но так как А'єl', то Аєl. Аналогично Аєm. Это противоречит параллельности прямых l и m.

рис. 8

2.При аффинном преобразовании сохраняется отношение двух отрезков, расположенных на одной прямой:  (рис.9)

В самом деле, по определению аффинного преобразования:

.

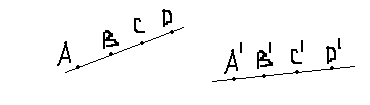
рис. 9

3.При аффинном преобразовании сохраняется отношение параллельных отрезков.

Дано: АВ||СD. По свойству 2 будет также А'В'||С'D'(рис.10)

Надо доказать:

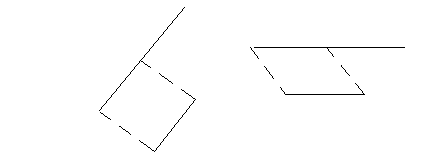
рис. 10

Для доказательства проведем АС, затем DL||AC. Построим также А'С' и D'L'||A'C'. По свойству 2 прямая DL переходит в D'L' и значит, . Теперь по определению: . Но AL=CD, A'L'=C'L', поэтому отсюда сразу получается требуемое.

4.При аффинном преобразовании угол и отношение произвольных отрезков, вообще говоря, не сохраняются, так как любой треугольник можно перевести в любой другой. Поэтому высота и биссектриса треугольника преобразуются обычно в другие линии, медиана же переходит в медиану, так как середина отрезка переходит в середину.

5. При аффинном преобразовании параллелограмм переходит в параллелограмм, трапеция в трапецию.

2.3 Эквивалентные фигуры

Аналогично понятию равенства и подобия фигур вводится понятие их аффинной эквивалентности.

Фигура F1 называется аффинно эквивалентной фигуре F2, если F1 можно аффинным преобразованием перевести в F2.

Корректность этого определения вытекает из того, что аффинные преобразования образуют группу и, следовательно, введенная здесь аффинная эквивалентность обладает транзитивностью, рефлексивностью, симметричностью.

Отметим некоторые классы аффинно эквивалентных фигур.

1). Все треугольники аффинно эквивалентны (следует из основной теоремы).

2). Все параллелограммы аффинно эквивалентны.

3). Для аффинной эквивалентности трапеций необходимо и достаточно, чтобы их основания были пропорциональны.

2.4 Перспективно-аффинное соответствие двух плоскостей

Предположим, что две плоскости w и w' пересекаются по линии хх (черт. 1). Зададим какую-нибудь прямую l, пересекающую обе плоскости. Отметим на плоскости w произвольную точку А и спроектируем ее на плоскость w', проводя через А прямую, параллельную l. Пусть проектирующая прямая пересечет плоскость w' в точке А'. Точку А' можно рассматривать как проекцию точки А на плоскость w'. Такая проекция называется параллельной и определяется заданием прямой l.

Из самого построения проекции А' точки А видно, что в свою очередь точку А можно рассматривать как проекцию точки А' на плоскость w. Таким образом, параллельная проекция представляет собой аппарат, имеющий совершенно одинаковое значение по отношению к обеим плоскостям w и w'. Она относит каждой точке (А) первой плоскости вполне определенную точку (А') второй, и обратно. Мы получаем попарное соответствие точек плоскостей w и w'. Это соответствие является взаимно однозначным, т. е. каждой точке одной плоскости соответствует единственная точка второй, и обратно.

Соответствие плоскостей w и w', установленное с помощью параллельной проекции, называется перспективно- аффинным или родственным.

Если рассматривают процесс перехода от одной из данных плоскостей (например, w) к другой плоскости (w'), при котором каждая точка (А) одной плоскости (w) переходит в соответствующую точку (А') другой плоскости (w'), как односторонний, то его называют преобразованием плоскости (w ) в плоскость (w')- В этом случае точку А называют прообразом, а точку А' - ее образом.

Проектируя параллельно плоскость w на плоскость w' , производим перспективно-аффинное преобразование плоскости w в плоскость w' .

Можно также совокупность всех точек плоскости w называть полем точек w и говорить о преобразовании поля точек w в поле точек w'.

Поставим себе задачу изучить свойства перспективно-аффинного соответствия плоскостей.

Займемся, прежде всего, вопросом о двойных, или неподвижных, точках нашего соответствия, т. е. о таких точках, которые совпадают со своими соответственными точками. Так как каждая двойная точка должна принадлежать как одной, так и другой плоскости, то они должны лежать на линии пересечения хх плоскостей w и w'. С другой стороны, очевидно, что каждая точка прямой хх есть двойная, так как она сама себе соответствует. Прямая называется осью соответствия. Согласно предыдущему ось соответствия может быть определена как геометрическое место двойных точек.

Рассмотрим далее какую-нибудь прямую АВ на плоскости w (черт. 1). Параллельная проекция этой прямой на плоскость w' есть прямая А'В'. Причем обе прямые либо пересекаются на оси хх, либо обе параллельны оси.

Таким образом, прямой линии на одной плоскости соответствует прямая же линия на другой. Это свойство перспективно-аффинного соответствия называют коллинеарностью. В силу самого определения параллельной проекции фигуры как геометрического места проекций всех точек этой фигуры каждой точке, лежащей на прямой, всегда соответствует точка, лежащая на соответственной прямой. Поэтому взаимопринадлежность точки и прямой на одной плоскости влечет за собой взаимопринадлежность соответственных элементов на второй.

2. Следующее свойство перспективно-аффинного соответствия касается так называемого простого отношения трех точек прямой.

Рассмотрим три точки А, В, С, лежащие на одной прямой (черт 1). Простое отношение точек А, В, С определяется формулой:

геометрический преобразование аффинный соответствие

В этой формуле точки А и В считаются основными (или базисными), а точка С- делящей. Простое отношение (ABC) представляет собой отношение длин тех отрезков, которые делящая точка образует с основными. Если точка С лежит вне отрезка А В, то оба отрезка АС и ВС одинаково направлены, и поэтому в этом случае простое отношение (ABC) положительно. В случае, когда делящая точка С находится между А и В, простое отношение (ABC) отрицательно.

На чертеже 1 видно, что точкам А,В, С плоскости w соответствуют точки А', В', С' плоскости w'. Так как проектирующие прямые АА', ВВ', СС' параллельны, то будем иметь:

или (ABC) = (А'В'С').

Мы приходим к выводу, что в перспективно-аффинном соответствии простое отношение трех точек прямой одной плоскости всегда равно простому отношению трех соответственных точек другой.

3. Прежде чем перейти к рассмотрению дальнейших свойств перспективно-аффинного соответствия, остановимся на вопросе о возможном расположении соответственных плоскостей w и w' в пространстве.

До сих пор мы предполагали эти плоскости несовпадающими и пересекающимися по линии хх с той целью, чтобы посредством параллельного проектирования установить рассмотренное выше перспективно-аффинное соответствие. После того как такое соответствие установлено, можно было бы привести обе плоскости в совпадение, вращая какую-либо одну из них вокруг оси хх. При этом все геометрические образы, находящиеся в той и другой плоскости, не подвергаются никакому изменению. Следовательно, как в любой момент вращения плоскости, так и при ее совмещении со второй плоскостью установленное ранее перспективно-аффинное соответствие не нарушается.

Прямые, соединяющие соответственные точки, как АА', ВВ', СС',…, остаются параллельными при любом положении вращающейся плоскости, а также и после ее совмещения с неподвижной плоскостью. Это видно из того, что каждые две из упомянутых прямых (например, АА' и ВВ') всегда лежат в одной плоскости, определяемой парой пересекающихся прямых (АВ и А'В'), и отсекают на сторонах угла пропорциональные отрезки, так как (АВХ) = (А'В'Х). При совмещении плоскостей w и w' проектирующие прямые (АА', ВВ',...) окажутся лежащими в плоскости, образовавшейся из двух совпавших плоскостей w и w' (черт. 2).

Для нас особенно интересен случай совмещенного положения плоскостей так как в этом случае мы можем пользоваться плоским чертежом, изображающим установленное соответствие без искажения.

В случае совмещения каждую точку (двойной) плоскости можно рассматривать как принадлежащую плоскости w или w' и обозначать ее в зависимости от этого большой буквой без штриха или со штрихом. Таким образом, мы имеем преобразование плоскости в себя, причем ее начальное состояние (плоскость до преобразования) обозначается буквой w, а новое состояние (плоскость после преобразования) - буквой w'.

Заметим, что после совмещения плоскостей ось соответствия хх перестает быть линией пересечения данных плоскостей, но за ней сохраняется второе определение как геометрического места двойных, или неподвижных, точек.

4.Теперь мы могли бы отказаться от пространственного аппарата (параллельной проекции), послужившего нам для установления перспективно-аффинного соответствия двух плоскостей, и определить последнее для двойной плоскости, не выходя в пространство. С этой целью докажем следующее предположение: Перспективно-аффинное преобразование плоскости в себя вполне определяется осью (хх) и парой соответственных точек (А, А').

Доказательство. Пусть даны ось хх и пара соответственных точек (АА') перспективно-аффинного преобразования (черт. 3). Докажем, что для любой точки В плоскости можно построить вполне определенную и единственную соответственную точку В'.

Проведем прямую АВ. Пусть X -точка ее пересечения с осью хх. Так как точка X сама себе соответствует (как лежащая на оси), то прямой АХ соответствует прямая А'X. Наконец, точка В' должна лежать на прямой А'Х и проектирующей прямой ВВ', параллельной А А'. Это позволяет построить искомую точку В'. Таким образом, данных оказалось достаточно, и соответственная точка В' представляет единственное решение.

Заметим, что перспективно-аффинное соответствие будет действительно реализовано, так как указанная конструкция не может привести к противоречию. Это легко проверить, сведя построение к аппарату параллельной проекции.

В самом деле, если перегнем чертеж 3 по линии хх так, чтобы плоскости w и w' образовали двугранный угол, то все проектирующие прямые (прямые, соединяющие соответственные точки, например ВВ') окажутся параллельными прямой АА' (в силу пропорциональности отрезков). Следовательно, построенное нами соответствие можно рассматривать как результат параллельной проекции.

Примечание. Если бы на чертеже 3 мы отнесли точку В к плоскости w', обозначив ее через С', то построение соответственной точки привело бы нас к точке С, которая, как видно из чертежа 3, не всегда совпадает с В'. Можно доказать, что необходимое и достаточное условие такого совпадения, т. е. независимости перспективно-аффинного соответствия от того, отнесена ли точка к той или другой плоскости, заключается в делении отрезка А А' пополам в точке пересечения его с осью хх.

Следовательно, в этом случае соответствие является косой или прямой симметрией (относительно оси хх).

5. В дальнейшем исследовании перспективно-аффинного соответствия мы будем опираться на установленные выше свойства: 1) коллинеарность и 2) равенство простых отношений троек соответственных точек.

Заметим, что в перспективно-аффинных преобразованиях эти свойства выражают неизменность, или инвариантность, понятия прямой линии и понятия простого отношения трех точек прямой.

Из этих свойств можно вывести целый ряд других «инвариантов» перспективно-аффинного преобразования, которые, таким образом, уже не являются независимыми. Докажем прежде всего инвариантность параллелизма прямых. Предположим, что на плоскости w имеем две прямые а и b, которым на плоскости w' соответствуют прямые а' и b'. Предположим, что прямые а и b параллельны (а || b). Докажем, что а '|| b'. Применим доказательство «от противного». Предположим, что прямые а' и b' пересекаются, и обозначим точку пересечения буквой М' (черт. 4). Тогда в силу взаимно однозначного соответствия плоскостей w и w' точке М' плоскости w' соответствует точка М на плоскости w. Точка М должна принадлежать как прямой а, так и прямой b. Следовательно, М есть точка пересечения прямых а и b. Таким образом, приходим к противоречию. Предположение, что прямые а' и b' пересекаются, невозможно. Поэтому а' || b'.

Таким образом, параллелизм прямых есть инвариантное свойство перспективно-аффинного преобразования.

Далее рассмотрим отношение двух параллельных отрезков. Пусть на плоскости w имеем два отрезка АВ и СD (черт. 5) и пусть АВ || СD. Им соответствуют на плоскости w' два также параллельных отрезка: А'В' \\ С'D'.

Соединим В с D и проведем через С прямую СF || DВ. На плоскости w' прямой СF будет соответствовать прямая С'F' \\D'В' (в силу инвариантности параллелизма) и, следовательно, точке F будет соответствовать точка F'. Зная, что простое отношение трех точек инвариантно, можем написать:

Таким образом, приходим к равенству:

Последнее показывает, что отношение двух параллельных отрезков есть инвариант перспективно-аффинного соответствия.

Если отрезки АВ и СD лежат на одной прямой (черт. 6), то их отношение также инвариантно в перспективно-аффинном соответствии. В самом деле, пусть РQ-произвольный отрезок, параллельный прямой АВ. Тогда имеем:

6. Переходим к рассмотрению площадей соответственных фигур. Докажем следующую лемму: Расстояния двух соответственных точек (А, А') до оси соответствия (хх) находятся в постоянном отношении, не зависящем от выбора пары соответственных точек. Доказательство. Предположим, что точкам А и В соответствуют точки А' и В' (черт. 7). Опуская из этих точек перпендикуляры на ось хх, получим расстояния их до оси. Расстояния будем всегда рассматривать положительными независимо от направления перпендикуляров.

Можем написать:

Но как видно из чертежа:

Полученное равенство и доказывает формулированную выше лемму.

Обозначим постоянное отношение расстояний соответственных точек через к. Докажем следующую теорему.

Отношение площадей двух соответственных треугольников постоянно и равно к.

Доказательство теоремы распадается на следующие случаи:

1.Треугольники имеют общую сторону на оси хх.

Такие треугольники представлены на чертеже 8. Отношение их площадей выразится следующим образом:

2. Треугольники имеют общую вершину на оси хх.

Таковы два треугольника на чертеже 9. Соответственные стороны ВС и В'С' этих треугольников должны пересекаться на оси хх (в точке X). Рассматриваемый случай сводится к предыдущему. В самом деле, на основании предыдущего можно написать:

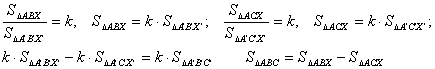
Но

Поэтому будем иметь:

3.Общий случай двух соответственных треугольников.

Пусть на чертеже 10 имеем два соответственных треугольника ABC и А'В'С'. Рассмотрим один из этих треугольников, например ABC. Площадь этого треугольника можно представить следующим образом:

Все треугольники правой части этого равенства относятся к рассмотренным уже двум случаям, поэтому, применяя к ним доказанную теорему, можем переписать найденное выше равенство так:

,или

Следовательно,

7. Выведенное нами свойство площадей двух соответственных треугольников легко распространить на случай соответственных многоугольников. В самом деле, каждый многоугольник может быть разбит на несколько треугольников, причем площадь многоугольника выразится суммой площадей составляющих его треугольников.

Для соответственного многоугольника получим аналогичное разбиение на треугольники. Если площади двух соответственных многоугольников обозначим буквами S и S', а площади двух соответственных составляющих треугольников — буквами , то можем написать:

Так как, кроме того, для площадей соответственных треугольников имеем:

, то

Таким образом, получаем:

Наконец, можно обобщить теорему об отношении площадей на случай двух площадей, ограниченных соответственными кривыми произвольного вида.

Обозначим площади, ограниченные двумя соответственными кривыми, через  и . Впишем многоугольник в кривую, ограничивающую площадь, и обозначим площадь этого многоугольника буквой S. Будем увеличивать число сторон вписанного многоугольника до бесконечности при условии, что каждая сторона его стремится к нулю, тогда получим:

Для площади  будем иметь аналогичный процесс: ,

где через S' обозначена площадь многоугольника, соответственного многоугольнику S. Так как в течение всего процесса (изменения многоугольников), согласно доказанной выше теореме, должны иметь:

S = kS',

то переход к пределу дает =k.

Следовательно,

Полученное свойство может быть представлено как инвариант перспективно-аффинного соответствия.

В самом деле, обозначим через и площади, ограниченные двумя кривыми произвольного вида, а через ' и ' - площади, ограниченные соответственными кривыми, тогда, по доказанному, будем иметь:

или, переставляя средние члены пропорции:

что может быть выражено следующими словами: отношение двух каких-либо площадей не изменяется (является инвариантом) в перспективно-аффинном соответствии.

Общее аффинное соответствие

Перспективно-аффинное соответствие двух плоскостей может быть получено с помощью параллельной проекции.

Рассмотрим теперь соответствие двух плоскостей, образованное многократным применением параллельного проектирования. Так, на чертеже 11 плоскость w проектируется параллельно прямой l на плоскость w'. Эта плоскость проектируется параллельно прямой l' на плоскость w". Наконец, последняя проектируется параллельно прямой l" на плоскость w'". Таким образом, между плоскостями w и w"'устанавливается соответствие, в котором точкам A,B,C первой плоскости соответствуют точки А'", В'", С" второй. Нетрудно убедиться в том, что это соответствие может не быть параллельной проекцией, но в то же время обладает инвариантными свойствами перспективно-аффинного соответствия. В самом деле, соответствие плоскостей w и w"' является цепью последовательных параллельных проектирований. Так как каждое такое проектирование сохраняет коллинеарность и простое отношение трех точек, то теми же свойствами должно, очевидно, обладать и результирующее соответствие плоскостей w и w'''.

То же самое можно сказать и об остальных инвариантных свойствах, рассмотренных в случае перспективно-аффинного соответствия, которое оказывается, таким образом, лишь тем частным случаем, когда прямые, соединяющие соответственные точки, параллельны между собой:

По этой именно причине такое соответствие называется перспективно- аффинным.

Соответствие же плоскостей w и w''' называется аффинным. Мы пришли к этому понятию, воспользовавшись цепью перспективно-аффинных преобразований (или параллельных проекций). Если каждое из них обозначим буквами Р, Р',Р" а результирующее преобразование — буквой А, можем представить аффинное преобразование А следующей символической формулой:

А = Р • Р' • Р",

в которой правая часть представляет собой «произведение» перспективно-аффинных преобразований, т. е. результат их последовательного применения.

Те же рассуждения можно было бы провести, не выходя из одной плоскости, для чего достаточно рассматривать цепь перспективно-аффинных преобразований плоскости в себя. Каждое из преобразований может быть задано осью и парой соответственных точек. Так, например, на чертеже 12 первое преобразование Р задано осью хх и парой (А, А'); второе Р' — осью и парой (А', А"); третье Р" — осью х"х" и парой (А'' А'"). В результирующем преобразовании А точке А соответствует точка А'". На том же чертеже показано построение точки В"', соответственной точке В.

Изложенное показывает, что преобразования, полученные при помощи цепи параллельных проекций (или перспективно-аффинных преобразований), обладают свойствами коллинеарности и сохранения простого отношения трех точек.

2.4 Применение аффинных преобразований при решении задач

Если в задаче затрагиваются только такие свойства фигур, которые сохраняются при произвольном аффинном преобразовании, то задача называется аффинной. Если же в задаче речь идет о свойствах, сохраняющихся при преобразованиях подобия, но нарушающихся при каком- либо аффинном преобразовании, то задача называется метрической. Например, задача «доказать, что медианы треугольника пересекаются в одной точке»- аффинная, а такие же задачи для высот и биссектрис- метрические.

Для решения аффинных задач рекомендуются следующие приемы:

1. Какую- либо из фигур аффинным преобразованием перевести в более простую, например, треугольник - в правильный треугольник, параллелограмм- в квадрат и т.д.

2. Применить аффинные координаты.

Эти идеи иллюстрируются первыми двумя из следующих задач.

1)Докажите, что прямая, соединяющая точку Р пересечения диагоналей трапеции АВСD с точкой пересечения Q боковых сторон, проходит через середины оснований трапеции.

Способ решения 1. Возьмем произвольный равнобедренный треугольник А'О'D'(рис.10) и рассмотрим аффинное преобразование α: . Обозначим точки пересечения прямой РQ с основаниями через х и у. Обозначим α(В)=В', α(С)=С', α(Р)=Р' и т.д. Очевидно, что точка Р' есть точка пересечения А'С' и В'D', точка х'- точка пересечения А'D' и Р'Q', точка у'- точка пересечения В'С' и Р'Q'. Так как . То достаточно показать, что .

Способ решения 2. Примем точку А за начало координат и возьмем такие координатные векторы: . Абсциссу точки C обозначим а. Имеем: А(0,0), В(0,1), С(а,1), D(1,0). Уравнение прямой CD найдем по двум точкам.

CD: х-у(1-а)-1-0

Решая это уравнение совместно с уравнением оси ОУ(х≠0) находим Q(0,1/(1-a))

Теперь найдем координаты точки Р. Решая совместно уравнения BD: x+y-1=0, AC: x-ay=0 находим: Р (а/(1+а),1/(1+а))

Находим уравнение PQ: 2х+у(1-а)-1=0 после чего находим к