Анализ временных рядов
В данной главе рассматриваются задачи описания упорядоченных данных, полученных последовательно (во времени). Вообще говоря, упорядоченность может иметь место не только во времени, но и в пространстве, например, диаметр нити как функция её длины (одномерный случай), значение температуры воздуха как функция пространственных координат (трёхмерный случай).
В отличие от регрессионного анализа, где порядок строк в матрице наблюдений может быть произвольным, во временных рядах важна упорядоченность, а следовательно, интерес представляет взаимосвязь значений, относящихся к разным моментам времени.
Если значения ряда известны в отдельные моменты времени, то такой ряд называют дискретным, в отличие от непрерывного, значения которого известны в любой момент времени. Интервал между двумя последовательными моментами времени назовём тактом(шагом). Здесь будут рассматриваться в основном дискретные временные ряды с фиксированной протяжённостью такта, принимаемой за единицу счёта. Заметим, что временные ряды экономических показателей, как правило, дискретны.
Значения ряда могут быть измеряемыми непосредственно (цена, доходность, температура), либо агрегированными (кумулятивными), например, объём выпуска; расстояние, пройдённое грузоперевозчиками за временной такт.
Если значения ряда определяются детерминированной математической функцией, то ряд называют детерминированным. Если эти значения могут быть описаны лишь с привлечением вероятностных моделей, то временной ряд называют случайным.
Явление, протекающее во времени, называют процессом, поэтому можно говорить о детерминированном или случайном процессах. В последнем случае используют часто термин “стохастический процесс”. Анализируемый отрезок временного ряда может рассматриваться как частная реализация (выборка) изучаемого стохастического процесса, генерируемого скрытым вероятностным механизмом.
Временные ряды возникают во многих предметных областях и имеют различную природу. Для их изучения предложены различные методы, что делает теорию временных рядов весьма разветвленной дисциплиной. Так, в зависимости от вида временных рядов можно выделить такие разделы теории анализа временных рядов:
– стационарные случайные процессы, описывающие последовательности случайных величин, вероятностные свойства которых не изменяются во времени. Подобные процессы широко распространены в радиотехнике, метереологии, сейсмологии и т. д.
– диффузионные процессы, имеющие место при взаимопроникновении жидкостей и газов.
– точечные процессы, описывающие последовательности событий, таких как поступление заявок на обслуживание, стихийных и техногенных катастроф. Подобные процессы изучаются в теории массового обслуживания.
Мы ограничимся рассмотрением прикладных аспектов анализа временных рядов, которые полезны при решении практических задач в экономике, финансах. Основной упор будет сделан на методы подбора математической модели для описания временного ряда и прогнозирования его поведения.
1.Цели, методы и этапы анализа временных рядов
Практическое изучение временного ряда предполагает выявление свойств ряда и получение выводов о вероятностном механизме, порождающем этот ряд. Основные цели при изучении временного ряда следующие:
– описание характерных особенностей ряда в сжатой форме;
– построение модели временного ряда;
– предсказание будущих значений на основе прошлых наблюдений;
– управление процессом, порождающим временной ряд, путем выборки сигналов, предупреждающих о грядущих неблагоприятных событиях.
Достижение поставленных целей возможно далеко не всегда как из-за недостатка исходных данных (недостаточная длительность наблюдения), так из-за изменчивости со временем статистической структуры ряда.
Перечисленные цели диктуют в значительной мере, последовательность этапов анализа временных рядов:
1) графическое представление и описание поведения ряда;
2) выделение и исключение закономерных, неслучайных составляющих ряда, зависящих от времени;
3) исследование случайной составляющей временного ряда, оставшейся после удаления закономерной составляющей;
4) построение (подбор) математической модели для описания случайной составляющей и проверка ее адекватности;
5) прогнозирование будущих значений ряда.
При анализе временных рядов используются различные методы, наиболее распространенными из которых являются :
1) корреляционный анализ, используемый для выявления характерных особенностей ряда (периодичностей, тенденций и т. д.);
2) спектральный анализ, позволяющий находить периодические составляющие временного ряда;
3) методы сглаживания и фильтрации, предназначенные для преобразования временных рядов с целью удаления высокочастотных и сезонных колебаний;
4) модели авторегрессии и скользящего среднего для исследование случайной составляющей временного ряда ;
5) методы прогнозирования.
2.Структурные компоненты временного ряда
Как уже отмечалось, в модели временного ряда принято выделять две основные составляющие : детерминированную и случайную (рис.). Под детерминированной составляющей временного ряда ![]() понимают числовую последовательность
понимают числовую последовательность ![]() , элементы которой вычисляются по определенному правилу как функция времени t. Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять чисто случайные скачки, а в другом – плавное колебательное движение. В большинстве случаев будет нечто среднее: некоторая иррегулярность и определенный систематический эффект, обусловленный зависимостью последовательных членов ряда.
, элементы которой вычисляются по определенному правилу как функция времени t. Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять чисто случайные скачки, а в другом – плавное колебательное движение. В большинстве случаев будет нечто среднее: некоторая иррегулярность и определенный систематический эффект, обусловленный зависимостью последовательных членов ряда.
В свою очередь, детерминированная составляющая может содержать следующие структурные компоненты:
1) тренд g, представляющий собой плавное изменение процесса во времени и обусловленный действием долговременных факторов. В качестве примера таких факторов в экономике можно назвать : а) изменение демографических характеристик популяции (численности, возрастной структуры); б) технологическое и экономическое развитие; в) рост потребления.
2) сезонный эффект , связанный с наличием факторов, действующих циклически с заранее известной периодичностью. Ряд в этом случае имеет иерархическую шкалу времени (например, внутри года есть сезоны, связанные с временами года, кварталы, месяцы) и в одноименных точках ряда имеют место сходные эффекты.
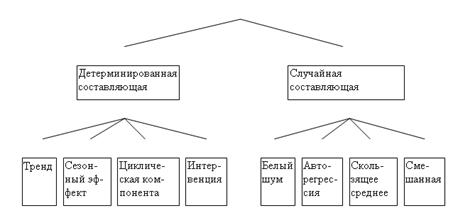
Рис. Структурные компоненты временного ряда.
Типичные примеры сезонного эффекта: изменение загруженности автотрассы в течение суток, по дням недели, временам года, пик продаж товаров для школьников в конце августа - начале сентября. Сезонная компонента со временем может меняться, либо носить плавающий характер. Так на графике объема перевозок авиалайнерами (см рис.) видно, что локальные пики, приходящиеся на праздник Пасхи «плавают» из-за изменчивости ее сроков.
Циклическая компонента c, описывающая длительные периоды относительного подъема и спада и состоящая из циклов переменной длительности и амплитуды. Подобная компонента весьма характерна для рядов макроэкономических показателей. Циклические изменения обусловлены здесь взаимодействием спроса и предложения, а также наложением таких факторов, как истощение ресурсов, погодные условия, изменения в налоговой политике и т. п. Отметим, что циклическую компоненту крайне трудно идентифицировать формальными методами, исходя только из данных изучаемого ряда.
«Взрывная» компонента i, иначе интервенция, под которой понимают существенное кратковременное воздействие на временной ряд. Примером интервенции могут служить события «черного вторника» 1994г., когда курс доллара за день вырос на несколько десятков процентов.
Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру, начиная от простейшей в виде «белого шума» до весьма сложных, описываемых моделями авторегрессии-скользящего среднего (подробнее дальше).
После выделения структурных компонент необходимо специфицировать форму их вхождения во временной ряд. На верхнем уровне представления с выделением лишь детерминированной и случайной составляющих обычно используют аддитивную либо мультипликативную модели.
Аддитивная модель имеет вид
![]() ;
;
мультипликативная –
![]() ,
,
где ![]() - значение ряда в момент t ;
- значение ряда в момент t ;
![]() - значение детерминированной составляющей;
- значение детерминированной составляющей;
![]() - значение случайной составляющей.
- значение случайной составляющей.
В свою очередь, детерминированная составляющая может быть представлена как аддитивная комбинация детерминированных компонент:
![]() ,
,
как мультипликативная комбинация:
![]() ,
,
либо как смешанная комбинация, например,
![]()
3.Модели компонентов детерминированной составляющей временного ряда
3.1.Модели тренда
Тренд отражает действие постоянных долговременных факторов и носит плавный характер, так что для описания тренда широко используют полиномиальные модели, линейные по параметрам
![]() ,
,
где значения степени k полинома редко превышает 5.
Наряду с полиномиальными моделями экономические данные, описывающие процессы роста, часто аппроксимируются следующими моделями:
– экспоненциальной
![]() .
.
Эта модель описывает процесс с постоянным темпом прироста, то есть
![]()
– логистической
![]()
У процесса, описываемого логистической кривой, темп прироста изучаемой характеристики линейно падает с увеличением y, то есть
![]()
– Гомперца
![]() .
.
Эта модель описывает процесс, в котором темп прироста исследуемой характеристики пропорционален ее логарифму
![]() .
.
Две последние модели задают кривые тренда S-образной формы, представляя процессы с нарастающим темпом роста в начальной стадии с постепенным замедлением в конце.
При подборе подходящей функциональной зависимости, иначе спецификации тренда, весьма полезным является графическое представление временного ряда.
Отметим также, что тренд, отражая действие долговременных факторов, является определяющим при построении долговременных прогнозов.
3.2 Модели сезонной компоненты
Сезонный эффект во временном ряде проявляется на «фоне» тренда и его выделение оказывается возможным после предварительной оценки тренда. (Здесь не рассматриваются методы спектрального анализа, позволяющего выделить вклад сезонной компоненты в спектр без вычисления других компонент ряда). Действительно, линейно растущий ряд помесячных данных будет иметь схожие эффекты в одноименных точках – наименьшее значение в январе и наибольшее в декабре; однако вряд ли здесь уместно говорить о сезонном эффекте: исключив линейный тренд, мы получим ряд, в котором сезонность полностью отсутствует. В то же время ряд, описывающий помесячные объемы продаж новогодних открыток, хотя и будет иметь такую же особенность (минимум продаж в январе и максимум в декабре) будет носить скорее всего колебательный характер относительно тренда, что позволяет специфицировать эти колебания как сезонный эффект.
В простейшем случае сезонный эффект может проявляться в виде строго периодической зависимости.
![]() , для любого t, где t - период сезонности.
, для любого t, где t - период сезонности.
В общем случае значения, отстоящие на tмогут быть связаны функциональной зависимостью, то есть
![]() .
.
К примеру, сезонный эффект сам может содержать трендовую составляющую, отражающую изменение амплитуды колебаний .
Если сезонный эффект входит в ряд аддитивно, то ![]() модель сезонного эффекта можно записать как
модель сезонного эффекта можно записать как
![]() ,
,
где ![]() - булевы, иначе индикаторные, переменные, по одной на каждый такт внутри периода t сезонности. Так, для ряда месячных данных
- булевы, иначе индикаторные, переменные, по одной на каждый такт внутри периода t сезонности. Так, для ряда месячных данных ![]() =0 для всех t, кроме января каждого года, для которого
=0 для всех t, кроме января каждого года, для которого ![]() =1 и так далее. Коэффициент
=1 и так далее. Коэффициент ![]() при
при ![]() показывает отклонение январских значений от тренда,
показывает отклонение январских значений от тренда, ![]() - отклонение февральских значений и так далее до
- отклонение февральских значений и так далее до ![]() . Чтобы снять неоднозначность в значениях коэффициентов сезонности
. Чтобы снять неоднозначность в значениях коэффициентов сезонности ![]() , вводят дополнительное ограничение, так называемое условие репараметризации, обычно
, вводят дополнительное ограничение, так называемое условие репараметризации, обычно
![]() .
.
В том случае, когда сезонный эффект носит мультипликативный характер, то есть
![]()
модель ряда с использованием индикаторных переменных можно записать в виде
![]()
Коэффициенты ![]() , в этой модели принято называть сезонными индексами.
, в этой модели принято называть сезонными индексами.
Для полностью мультипликативного ряда
![]()
обычно проводят процедуру линеаризации операцией логарифмирования
![]() .
.
Условимся называть представленные модели сезонного эффекта «индикаторными». Если сезонный эффект достаточно «гладкий» – близок к гармонике, используют «гармоническое» представление
![]() ,
,
где d - амплитуда, w - условия частоты (в радианах в единицу времени), a - фаза волны. Поскольку фаза обычно заранее неизвестна. Последнее выражение записывают как
![]() ,
,
где ![]() ,
, ![]() .
.
Параметры А и В можно оценить с помощью обычно регрессии. Угловая частота wсчитается известной. Если качество подгонки окажется неудовлетворительным, наряду с гармоникой wосновной волны в модель включают дополнительно первую гармонику (с удвоенной основной частотой 2w), при необходимости и вторую и так далее гармоники. В принципе, из двух представлений: индикаторного и гармоничного – следует выбирать то, которое потребует меньшего числа параметров.
3.3 Модель интервенции
Интервенция, представляющая собой воздействие, существенно превышающее флуктуации ряда, может носить характер «импульса» или «ступеньки».
Импульсное воздействие кратковременно: начавшись, оно почти тут же заканчивается. Ступенчатое воздействие длительно, носит устойчивый характер. Обобщенная модель интервенции имеет вид
![]() ,
,
где ![]() - значение детерминированной компоненты ряда, описываемой как интервенция;
- значение детерминированной компоненты ряда, описываемой как интервенция;
![]() - коэффициенты типа авторегрессии;
- коэффициенты типа авторегрессии;
![]() - коэффициенты типа скользящего среднего;
- коэффициенты типа скользящего среднего;
![]() - экзогенная переменная одного из двух типов;
- экзогенная переменная одного из двух типов;
![]() («ступень»), или
(«ступень»), или ![]() («импульс»)
(«импульс»)
где ![]() -- фиксированный момент времени, называемый моментом интервенции.
-- фиксированный момент времени, называемый моментом интервенции.
4.Методы выделения тренда
Приведенные в п.3.1 спецификации ряда являются параметрическими функциями времени. Оценивание параметров может быть проведено по методу наименьших квадратов так же, как в регрессионном анализе. Хотя статистические предпосылки регрессионного анализа (см п. ) во временных рядах часто не выполняются (особенно п.5 – некоррелированность возмущений), тем не менее оценки тренда оказываются приемлемыми, если модель специфицирована правильно и среди наблюдений нет больших выбросов. Нарушение предпосылок регрессионного анализа сказывается не столько на оценках коэффициентов, сколько на их статистических свойствах, в частности, искажаются оценки дисперсии случайной составляющей и доверительные интервалы для коэффициентов модели.
В литературе описываются методы оценивания в условиях коррелированности возмущений, однако их применение требует дополнительной информации о корреляции наблюдений.
Главная проблема при выделении тренда состоит в том, что подобрать единую спецификацию для всего временного часто невозможно, поскольку меняются условия протекания процесса. Учет этой изменчивости особенно важен, если тренд вычисляется для целей прогнозирования. Здесь сказывается особенность именно временных рядов: данные относящиеся к «далекому прошлому» будут неактуальными, бесполезными или даже «вредными» для оценивания параметров модели текущего периода. Вот почему при анализе временных рядов широко используются процедуры взвешивания данных.
Для учета изменчивости условий модель ряда часто наделяют свойством адаптивности, по крайней мере, на уровне оценок параметров. Адаптивность понимается в том смысле, что оценки параметров легко пересчитываются по мере поступления новых наблюдений. Конечно, и обычному методу наименьших квадратов можно придать черты адаптивности, пересчитывая оценки каждый раз, вовлекая в процесс вычислений старые данные плюс свежие наблюдения. Однако при этом каждый новый пересчет ведет к изменению прошлых оценок, тогда как адаптивные алгоритмы свободны от этого недостатка.
4.1 Скользящие средние
Метод скользящих средних – один из самых старых и широко известных способов выделения детерминированной составляющей временного ряда. Суть метода состоит в усреднении исходного ряда на интервале времени, длина которого выбрана заранее. При этом сам выбранный интервал скользит вдоль ряда, сдвигаясь каждый раз на один такт вправо (отсюда название метода). За счет усреднения удается существенно уменьшить дисперсию случайной составляющей.
Ряд новых значений становится более гладким, вот почему подобную процедуру называют сглаживанием временного ряда.
Процедуру сглаживания рассмотрим вначале для ряда, содержащего лишь трендовую составляющую, на которую аддитивно наложен случайных компонент.
Как известно, гладкая функция может быть локально представлена в виде полинома с довольно высокой степенью точности. Отложим от начала временного ряда интервал времени длиной (2m+1) точек и построим полином степени m для отобранных значений и используем этот полином для определения значения тренда в (m+1)-й, средней, точке группы.
Построим для определенности полином 3-го порядка для интервала из семи наблюдений. Для удобства дальнейших преобразований занумеруем моменты времени внутри выбранного интервала так, чтобы его середина имела нулевое значение, т.е. t= -3, -2, -1, 0, 1, 2, 3. Запишем искомый полином:
![]() .
.
Константы ![]() находим методом наименьших квадратов:
находим методом наименьших квадратов:
![]() .
.
Дифференцируем по коэффициентам ![]() :
:
![]()
![]() ;
;
![]() ;
;
![]() .
.
Суммы нечетных порядков t от -3 до +3 равны 0, и уравнения сводятся к виду:
![]()
![]() ;
;
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]() .
.
Используя первое и третье из уравнений, получаем при t=0:
![]()
![]() (1)
(1)
Следовательно, значение тренда в точке t= 0 равно средневзвешенному значению семи точек с данной точкой в качестве центральной и весами
![]() , которые в силу симметрии можно записать короче:
, которые в силу симметрии можно записать короче:
![]() .
.
Для того чтобы вычислить значение тренда в следующей, (m+2)-й точке исходного ряда (в нашем случае пятой), следует воспользоваться формулой (1), где значения наблюдений берутся из интервала, сдвинутого на такт вправо, и т.д. до точки N-m .
Далее приводятся формулы для подсчета скользящего среднего подбором полиномов второго и третьего порядка к отрезкам ряда длиной до 9 точек:
количество точек формула
5 ![]()
7 ![]()
9 ![]() .
.
Свойства скользящих средних:
1) сумма весов равна единице (т.к. сглаживание ряда , все члены которого равны одной и той же константе, должно приводить к той же константе);
2) веса симметричны относительно серединного значения ;
3) формулы не позволяют вычислить значения тренда для первых и последних m значений ряда;
4) можно вывести формулы для построения трендов на четном числе точек, однако при этом были бы получены значения трендов в серединах временных тактов. Значение тренда в точках наблюдений можно определить в этом случая как полусумма двух соседних значений тренда.
Следует отметить, что при четном числе 2mтактовв интервале усреднения (двадцать четыре часа в сутки, четыре недели в месяце, двенадцать месяцев в году), широко практикуется простое усреднение с весами ![]() . Пусть имеются, например, наблюдения на последний день каждого месяца с января по декабрь. Простое усреднение 12 точек с весами
. Пусть имеются, например, наблюдения на последний день каждого месяца с января по декабрь. Простое усреднение 12 точек с весами ![]() дает значение тренда в середине июля. Чтобы получить значение тренда на конец июля надо взять среднее значение тренда в середине июля и середине августа. Оказывается, это эквивалентно усреднению 13-месячных данных, но значения на краях интервала берут с весами
дает значение тренда в середине июля. Чтобы получить значение тренда на конец июля надо взять среднее значение тренда в середине июля и середине августа. Оказывается, это эквивалентно усреднению 13-месячных данных, но значения на краях интервала берут с весами ![]() . Итак, если интервал сглаживания содержит четное число 2m точек, в усреднении задействуют не 2m, а 2m+1 значений ряда :
. Итак, если интервал сглаживания содержит четное число 2m точек, в усреднении задействуют не 2m, а 2m+1 значений ряда :
![]() .
.
Скользящие средние, сглаживая исходный ряд, оставляют в нем трендовую и циклическую составляющие. Выбор величины интервала сглаживания должен делаться из содержательных соображений. Если ряд содержит сезонный компонент, то величина интервала сглаживания выбирается равной или кратной периоду сезонности. В отсутствии сезонности интервал сглаживания берется обычно в диапазоне три-семь
Эффект Слуцкого-Юла
Рассмотрим, как влияет процесс сглаживания на случайную составляющую ряда, относительно которой будем полагать, что она центрирована и соседние члены ряда некоррелированы.
Скользящее среднее случайного ряда x есть:
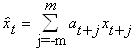 .
.
В силу центрированности xи отсутствия корреляций между членами исходного ряда имеем:
![]() и
и 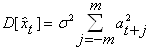 .
.
Далее, ![]() .
.
Из полученных соотношений видно, что усреднение приводит к уменьшению дисперсии колебаний. Кроме того члены ряда, полученные в результате усреднения, не являются теперь независимыми. Производный, сглаженный, ряд имеет ненулевые автокорреляции (корреляции между членами ряда, разделенных k-1 наблюдениями) вплоть до порядка 2m. Таким образом производный ряд будет более гладким, чем исходный случайный ряд, и в нем могут проявляться систематические колебания. Этот эффект называется эффектом Слуцкого-Юла .
4.2 Определение порядка полинома методом последовательных разностей
Если имеется ряд, содержащий полином (или локально представляемый полиномом) с наложенным на него случайным элементом , то было бы естественно исследовать, нельзя ли исключить полиномиальную часть вычислением последовательных разностей ряда. Действительно, разности полинома порядка k представляют собой полином порядка k-1. Далее , если ряд содержит полином порядка p , то переход к разностям , повторенный (p+1) раз, исключает его и оставляет элементы, связанные со случайной компонентой исходного ряда.
Рассмотрим, к примеру, переход к разностям в ряде, содержащим полином третьего порядка.
![]() 0 1 8 27 64 125
0 1 8 27 64 125
![]() 1 7 19 37 61
1 7 19 37 61
![]() 6 12 18 24
6 12 18 24
![]() 6 6 6
6 6 6
![]() 0 0
0 0
Взятие разностей преобразует случайную составляющую ряда.
В общем случае получаем :
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
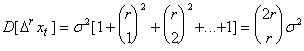 .
.
Из последнего соотношения получаем
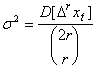 .
.
Следовательно, метод последовательных разностей переменной состоит в вычислении первых, вторых, третьих и т.д. разностей , определении сумм квадратов, делении на ![]() и т.д. и обнаружения момента , когда это отношение становится постоянным. Таким образом мы получаем оценки порядка полинома , содержащегося в исходном ряде, и дисперсии случайного компонента.
и т.д. и обнаружения момента , когда это отношение становится постоянным. Таким образом мы получаем оценки порядка полинома , содержащегося в исходном ряде, и дисперсии случайного компонента.
4.3.Методы экспоненциального сглаживания
Методы построения функций для описания наблюдений до сих пор основывался на критерии наименьших квадратов, в соответствии с которым все наблюдения имеют равный вес. Однако, можно предположить, что недавним точкам следует придавать в некотором смысле больший вес, а наблюдения, относящиеся к далекому прошлому, должны иметь по сравнению с ними меньшую ценность. До некоторой степени мы учитывали это в скользящих средних с конечной длиной отрезка усреднения, где значения весов, приписываемых группе из 2m+1 значений, не зависят от предшествующих значений. Теперь обратимся к другому методу выделения более «свежих» наблюдений.
Рассмотрим ряд весов, пропорциональных множителю b, а именно Рассмотрим простейший ряд Будем считать, что ряд имеет бесконечную предысторию, т. е. время принимает значения t,t-1,t-2,..., - ¥ . Найдем оценку В приведенном выражении расхождения между наблюденными значениями ряда и оценкой уровня берутся с экспоненциально убывающими весами в зависимости от возраста данных. Полученную оценку Полученное соотношение Перепишем несколько иначе, введя так называемую постоянную сглаживания Из полученного соотношения видно, что новое сглаженное значение получается из предыдущего коррекцией последнего на долю ошибки, рассогласования, между новым и прогнозным значениями ряда. Происходит своего рода адаптация уровня ряда к новым данным. Обобщим метод экспоненциального сглаживания на случай , когда модель процесса определяется линейной функцией (Здесь для удобства представления знаки ~ и Ù опущены). С учетом того что получаем Запишем : Эту операцию можно рассматривать как сглаживание 1-го порядка. По аналогии построим сглаживание 2-го порядка: ß Рассмотренную выше процедуру можно обобщить на случай полиномиальных трендов более высокого порядка n , при этом алгебраические выражения будут сложнее. Например, если модель описывается параболой, то используется метод тройного экспоненциального сглаживания. Сезонные компоненты могут представлять самостоятельный интерес либо выступать в роли мешающего фактора. В первом случае необходимо уметь выделять их из ряда и оценивать параметры соответствующей модели. Что же касается удаления сезонной компоненты из ряда, то здесь возможны несколько способов. Рассмотрим сначала процедуру оценивания сезонных эффектов. Пусть исходный ряд является полностью аддитивным, то есть Необходимо оценить Как уже отмечалось, сезонный эффект проявляется на фоне тренда, поэтому вначале необходимо оценить трендовую составляющую одним из рассмотренных методов. Затем для каждого сезона где, как обычно, Каждая из этих разностей дает совместную оценку сезонного эффекта и случайного компонента, отличного, правда, от исходного Производя усреднение полученных разностей, получают оценки эффектов. Полагая, что исходный ряд содержит целое число k периодов сезонности и ограничиваясь простым средним, имеем С учетом условия репараметризации, требующим, чтобы сумма сезонных эффектов равнялась нулю, получаем скорректированные оценки В случае мультипликативного сезонного эффекта, когда модель ряда имеет вид вычисляют уже не разности, а отношения В качестве оценки сезонного индекса На практике считается, что для оценки сезонных эффектов временной ряд должен содержать не менее пяти-шести периодов сезонности. Перейдем теперь к способам удаления сезонного эффекта из ряда. Таких способов два. Первый из них назовем «послетрендовый». Он является логическим следствием рассмотренной выше процедуры оценивания. Для аддитивной модели удаление сезонной компоненты сводится к вычитанию оцененной сезонной компоненты из исходного ряда. Для мультипликативной модели значения ряда делят на соответствующие сезонные индексы. Второй способ не требует предварительной оценки ни трендовой, ни сезонной компонент, а основывается на использовании разностных операторов. Разностные операторы. При исследовании временных рядов часто имеется возможность представить детерминированные функции времени простыми рекуррентными уравнениями. К примеру, линейный тренд можно записать как Последнее соотношение получается из (1) сравнением двух значений ряда для соседних моментов t-1 и t . Учитывая, что соотношение (2) справедливо и для моментов t-2 и t-1, так что Модель (3) не содержит явно параметров, описывающих тренд. Более компактно описанные преобразования можно описать, используя операторы взятия разности назад Модели (2) и (3) можно записать как Выходит, разность второго порядка полностью исключает из исходного ряда линейный тренд. Легко видеть, что разность порядка dисключает из ряда полиномиальный тренд порядка d-1. Пусть теперь ряд содержит сезонный эффект с периодом t, так что Процедура перехода от ряда Выходит, взятие сезонной разности Иногда оказываются полезными сезонные операторы более высоких порядков. Так, сезонный оператор второго порядка с периодом t есть Если ряд содержит и тренд, и сезонную составляющую, их можно исключить, последовательно применяя операторы Легко показать, что порядок применения этих операторов не существенен: Отметим также, что детерминированный тренд, состоящий из тренда и сезонной компоненты, после применения операторов Из последнее соотношения видно, каким образом ряд можно неограниченно продолжать, имея вначале по крайней мере t+1 последовательных значения.
![]() и т.д. Так как сумма весов должна равняться единице, т.е.
и т.д. Так как сумма весов должна равняться единице, т.е. ![]() , весами фактически будут
, весами фактически будут ![]() и т.д. ( предполагается , что 0
и т.д. ( предполагается , что 0
4.3.1 Простое экспоненциальное сглаживание
![]() , равный сумме постоянной
, равный сумме постоянной ![]() (уровень) и случайной компоненты
(уровень) и случайной компоненты ![]() :
:![]() .
.![]() уровня ряда
уровня ряда ![]() , воспользовавшись минимизацией взвешенной суммы квадратов:
, воспользовавшись минимизацией взвешенной суммы квадратов:![]() .
.![]() ;
; ![]() ;
; ![]() .
.![]() на момент t обозначим
на момент t обозначим ![]() (t). Сглаженное значение в момент t можно выразить через сглаженное значение в прошлый момент t-1 и новое наблюдение
(t). Сглаженное значение в момент t можно выразить через сглаженное значение в прошлый момент t-1 и новое наблюдение ![]() :
:![]()
![]()
![]()
![]() (t) =
(t) =![]()
![]() (0 £ a£1).
(0 £ a£1).![]() (t)
(t) ![]() ,
,
4.3.2 Экспоненциальное сглаживание высоких порядков
![]() . Как и прежде, при заданном b минимизируем:
. Как и прежде, при заданном b минимизируем:![]() .
.![]() ,
,![]()
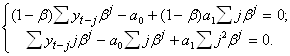
![]() ,
, ![]() ,
,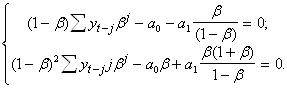
![]() .
.![]()
![]() .
.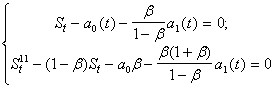
![]() ;
; ![]() .
.![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
5. Оценивание и исключение сезонной компоненты![]() .
.![]() по наблюденным
по наблюденным ![]() . Иными словами, необходимо получить оценки
. Иными словами, необходимо получить оценки ![]() коэффициентов
коэффициентов ![]() индикаторной модели.
индикаторной модели. ![]() вычисляют все относящиеся к нему разности
вычисляют все относящиеся к нему разности ![]()
![]() - наблюденное значение ряда,
- наблюденное значение ряда, ![]() - оцененное значение тренда.
- оцененное значение тренда. ![]() в силу взятия разностей.
в силу взятия разностей.![]()
![]() .
.![]() ,
,![]() .
.![]() выступает среднее
выступает среднее![]() .
.![]() (1)
(1)![]() (2)
(2) ![]() , модель (1) можно записать и в виде
, модель (1) можно записать и в виде ![]() (3)
(3)![]() .
.![]() .
.![]() ,
, ![]() .
.![]() (4).
(4).![]() (t= 1,2,...,T) к ряду
(t= 1,2,...,T) к ряду ![]() называется взятием первой сезонной разности, а оператор
называется взятием первой сезонной разности, а оператор ![]() сезонным разностным оператором с периодом t. Из (4) следует, что
сезонным разностным оператором с периодом t. Из (4) следует, что ![]() .
.![]() исключает из временного ряда
исключает из временного ряда ![]() любую детерминированную сезонную компоненту.
любую детерминированную сезонную компоненту.![]() .
.![]() и
и ![]() .
.![]() .
.![]() и
и ![]() полностью вырождается, то есть
полностью вырождается, то есть ![]() . Однако записав последнее уравнение в рекуррентной форме, получаем
. Однако записав последнее уравнение в рекуррентной форме, получаем![]() .
.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Классический метод наименьших квадратов
- Анализ и обобщение статистических данных экономики Республики Калмыкия
- Анализ методов прогнозирования и моделирование нейронных сетей для прогнозирования стоимости недвижимости
Переход к рыночным отношениям в экономике и научно-технический прогресс чрезвычайно ускорили темпы внедрения во все сферы социально-э
- Модель рекламной кампании
- Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙУНИВЕРСИТЕТ имени ВЛАДИМИРА ДАЛЯПОЯСНИТЕЛЬНАЯ ЗАПИСКАк курс
- Анализ хозяйственной и финансовой деятельности предприятия на примере ООО "НПРС-1"
- Иностранные инвестиции и занятость в Украине
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

