Скачать

Аксонометричні проекції

Житомирський Військовий Інститут

Національного Авіаційного Уніврситету

Реферат

на тему:

Аксонометричні проекції

Житомир 2010

План

1. Загальні відомості та основні положення

2. Стандартні види аксонометричних проекцій. Ізометрія, диметрія, способи їх побудови (осі, коефіцієнти спотворень)

Загальний висновок

Література

1. Загальні відомості та основні положення

Креслення, які виконані методом ортогонального проекціювання, мають ряд важливих особливостей, головною з яких є зручність вимірювання. В той же час для одержання уявлення про виріб необхідно розглядати декілька виглядів, часто доповнених перерізами, розрізами, додатковими і місцевими виглядами, виносними елементами. Все це ускладнює на перших етапах вивчення креслення формування уявлення про виріб.

У техніці для наочного зображення виробів або їх складових частин застосовуються аксонометричні проекції цих предметів. Вони порівняно з комплексним кресленням мають істотну перевагу – наочність, але створюють незручності при вимірюванні.

Слово «аксонометрія» - грецьке. Воно складається з двох слів: axon – вісь, metreo – вимірюю, що в перекладі означає «вимірювання по осях».

Побудова аксонометричних проекцій допомагає навчитися читати креслення і розвиває просторове уявлення про форму предметів і деталей.

Аксонометричні проекції застосовуються як допоміжні до комплексних креслень у тих випадках, коли необхідне пояснююче наочне зображення форми деталей.

Відмінність аксонометричних проекцій від ортогональних полягає в тому, що в аксонометричній проекції зображення предмета разом з осями координат одержується проекціюванням паралельними променями на одну аксонометричну площину проекцій.

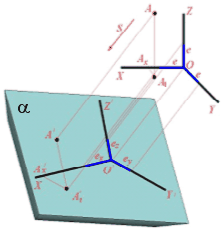
На рис. 1 показана схема проекціювання осей координат та віднесеної до них точки А на площину a. Направлення проекціювання вказано стрілкою S. Одержані при такому проекціюванні аксонометричні осі X', Y', Z' будуть проекціями осей X, Y, Z комплексного креслення. О' — аксонометрична проекція початку координат. Точка А' – аксонометрична проекція точки А; точка А'₁ представляє собою аксонометричну проекцію точки А₁. Якщо на кожній з координатних осей Х, У, Z (див. рис. 1) відкласти від точки О відрізки е_х, е_у, е_z, довжини яких дорівнюють одиниці натурального масштабу е, то внаслідок проекціювання одержимо е_Х, е_Y, е_Z — аксонометричні одиниці виміру. В загальному випадку е_Х, е_Y, е_Zне рівні e та не рівні між собою.

Відношення аксонометричної одиниці виміру е' до одиниці натурального масштабу е визначає показник спотворення по аксонометричній вісі.

Відношення довжини аксонометричної проекції відрізка, розташованого вдовж визначеної координатної осі або паралельно до неї, до натуральної довжини цього відрізка, називається коефіцієнтом спотворення.

Але при побудові аксонометричних проекцій звичайно користуються не самими коефіцієнтами спотворення, а деякими величинами, їм пропорційними. Ці величини будемо називати приведеними коефіцієнтами спотворення.

Відношення між аксонометричними проекціями відрізків, які паралельні осям координат X, Y, Z та самим відрізкам рівні коефіцієнтам

K_Х = е_Х /e, K_Y = е_Y /e, K_Z = e_Z /e.

Тому сутність аксонометричного методу полягає в тому, що об’єкт відносять до прямокутної системи координат та проекціюють його разом з осями координат паралельними променями на деяку площину проекцій, яку називають аксонометричною. Зображення, яке при цьому отримують, називають аксонометричним, а проекції осей координат - аксонометричними осями координат.

Щоб побудувати аксонометрію предмета, спочатку необхідно віднести його до системи трьох взаємно перпендикулярних площин, що збігаються з площинами проекцій, вибрати площину і напрям проекціювання, а потім побудувати на основі паралельного проекціювання за заданим напрямом на площині проекцію предмета разом з прямокутними координатними осями.

Зображення об’єкта на аксонометричній площині і напрям аксонометричних осей залежать від положення площини відносно системи координатних осей, а також від напряму проекціювання.

Якщо напрям проекціювання S перпендикулярний до площини проекцій Р, то аксонометричні проекції називають прямокутними (j = 90°). До прямокутних аксонометричних проекцій відносяться ізометрична і диметрична.

Якщо напрям проекціювання S не перпендикулярний до площини проекцій a, то аксонометричні проекції називають косокутними (j ¹ 90°). До косокутних аксонометричних проекцій відносяться: фронтальна ізометрична, горизонтальна ізометрична і фронтальна диметрична проекції.

Залежно від того, по скількох осях показники спотворення однакові, визначають той чи інший вид аксонометрії, а саме:

ізометрична проекція (ізометрія) — однакові всі три показники спотворення (K_Х = K_Y = K_Z);

диметрична проекція (диметрія) — однакові два з трьох показників

(K_Х — K_Y ¹ K_Z; K_Х = K_Y ¹ K_Z; K_Х ¹ K_Y = K_Z);

триметрична проекція (триметрія) — показники різні

(K_Х ¹ K_Y ¹ K_Z).

1. Сутність аксонометричного методу полягає в тому, що об’єкт відносять до прямокутної системи координат та проекціюють його разом з осями координат паралельними променями на деяку площину проекцій, яку називають аксонометричною. Зображення, яке при цьому отримують, називають аксонометричним, а проекції осей координат - аксонометричними осями координат.

2. Відношення довжини аксонометричної проекції відрізка, розташованого вдовж визначеної координатної осі або паралельно до неї, до натуральної довжини цього відрізка, називається коефіцієнтом спотворення.

2. Стандартні види аксонометричних проекції. Ізометрія, диметрія, способи їх побудови (осі, коефіцієнти спотворень)

Найчастіше в кресленні застосовуються прямокутні аксонометричні проекції, оскільки вони дають найбільш наочні зображення.

У табл. 1 наведено найменування видів аксонометричних проекцій, розташування їх осей і коефіцієнти (показники) спотворення розмірів по осях.

СТАНДАРТНІ АКСОНОМЕТРИЧНІ ПРОЕКЦІЇ

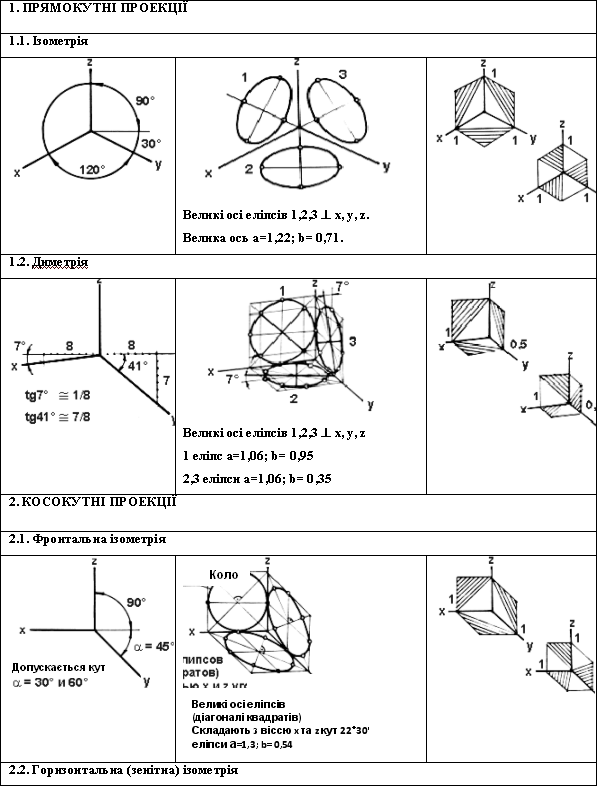
При цьому використовуються наведені у таблиці коефіцієнти спотворення: для ізометричних проекцій K_Х = K_Y = K_Z= 1, для диметричних проекцій K_Х = K_Z= 1; K_Y = 0,5.

При побудові аксонометричних проекцій користуються основною властивістю аксонометрії (це - паралельність проекцій): якщо дві прямі паралельні одна одної в просторі, то вони паралельні між собою в аксонометрії.

Побудова зображень не залежить від виду аксонометрії й полягає в побудові будь-якої геометричної фігури за допомогою координат точок цієї фігури. При цьому предмет має розташовуватися так, щоб його було видно спереду, збоку і зверху.

Побудова геометричних фігур в аксонометрії по заданих ортогональних проекціях

Побудову аксонометрії починають із призначення координатних осей в ортогональних проекціях. Оскільки поверхня предмета складається з ліній, а лінія з точок, то побудову аксонометричної проекції почнемо з точки. Перехід від ортогональних проекцій до аксонометричного зображення будують за алгоритмом:

1) на ортогональному кресленні розмічають осі координат;

2) будують аксонометричні осі;

3) по характерних точках будують аксонометричне зображення.

Прямокутна ізометрична проекція. Нехай задані ортогональні проекції точок А і В (рис. 2,а), то для побудови ізометричної проекції цих точок проводять аксонометричні осі x', y', z' під кутом 120° одна до одної. Далі, від початку координат О' по осі О'x' відкладають відрізок О'1' , що дорівнює координаті х точки В. Координату х беремо з комплексного креслення.

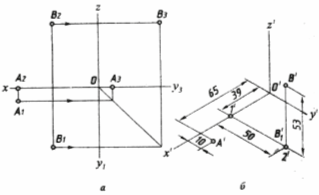
З точки 1' проводять пряму, паралельну осі y', і на ній відкладають відрізок 1'2', що дорівнює координаті y точки В; з точки 2' проводять пряму, паралельну осі z', на якій відкладають відрізок 2'В', котрий дорівнює координаті z точки В. Одержана точка В' – шукана ізометрична проекція точки В.

Для побудови ізометричної проекції точки А достатньо двох координат х і y, так як третя координата z дорівнює нулю, оскільки точка А лежить на площині π₁ .

Аксонометричні осі, а також відрізки прямих, які паралельні осям, зручно будувати за допомогою креслярського трикутника з кутами 30° та 60° (рис. 2).

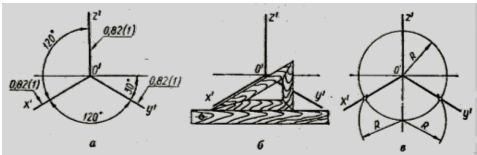
На рис. 2 показані різні прийоми побудови осей ізометрії: на рис. 2 ,б побудова здійснена за допомогою трикутника з кутами 30, 60, 90°; на рис. 2 ,в побудова здійснена за допомогою циркуля.

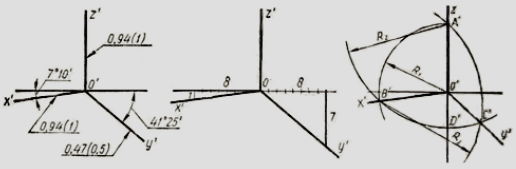
На рис. 3 показані різні прийоми побудови осей диметрії: 1 –й спосіб - на рис. 3 ,б . На горизонтальній прямій, яка проходить через точку О' відкладають по обидві сторони від О' вісім рівних довільних відрізків. З останніх точок цих відрізків вниз по вертикалі відкладають зліва один такий відрізок, а з права – сім. Отримані точки з'єднують з точкою О' та отримують аксонометричні осі О' х' та О' у' .

2 –й спосіб - на рис. 3 ,в . На вертикальній прямій вниз від точки О' відкладають відрізок довільної довжини (О'D'), а вверх – два таких же відрізка (О'А'= 2 О'D' ). З точки О', як з центру проводять дугу кола радіусом R₁ = О' А' до перетину в точці В' з дугою, проведеною з центру А' радіусом R₂ = А'D' . Пряма О'В' - направлення аксонометричної осі х' . Третю дугу радіусом R₃ = В'А' проводять з центру В' до перетину з дугою радіуса R₂ в точці С'. Пряма О'С' – направлення аксонометричної осі у' прямокутної диметрії.

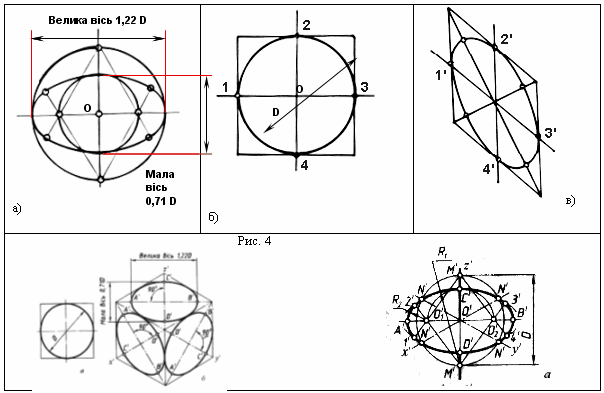
Найбільш трудомістким є побудова кіл. У прямокутних проекціях коло, розташовано в площинах p₁, p₂, p₃, або їм паралельним, проекціюється в еліпси, причому більша вісь еліпса перпендикулярна z, y, x відповідно (див. табл. 1). Еліпси заміняються овалами, які будуються по наведеним у таблиці значенням великих і малих осей (рис. 4,а). Слід запам’ятати , що мала вісь кожного еліпса завжди має бути перпендикулярна до його великої осі.

Для побудови кола користуються описаним навколо кола квадратом.

Чотирьом точкам торкання квадрата й кола (рис. 4,б) будуть відповідати 4 точки торкання 1', 2', 3', 4' в аксонометрії (рис. 4,в). Ще чотири точки належать кінцям великого й малого діаметра еліпса (табл.1).

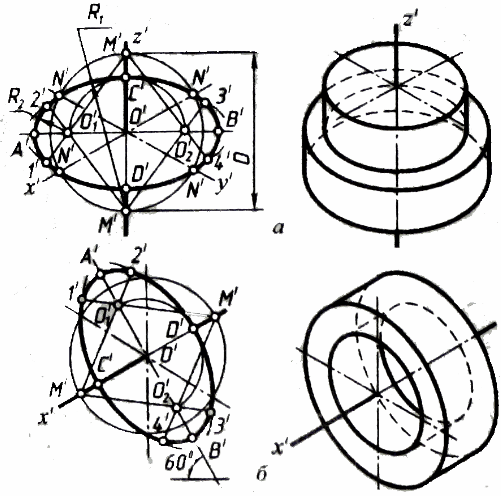
Для побудови овалу в площині паралельній p₁ , проводять вертикальну і горизонтальну осі овалу. З точки перетину О' проводять допоміжне коло діаметром D , що дорівнює дійсній величині діаметра зображуваного кола, і знаходять точки N' перетину цього кола з аксонометричними осями x' та y' . З точок М' перетину допоміжного кола з віссю z', як з центрів радіусом R₁= N'M' проводять дві дуги N'D'N' та N'С'N' кола, які належать овалу.

З центра О' радіусом О'С', що дорівнює половині малої осі овалу, засікають на великій осі овалу А'В' точки О'₁ і О'₂. З цих точок радіусом R₂= О'₁1' = О'₁2' = О'₂3' = О'₂4' проводять дві дуги. Точки 1', 2', 3', 4' спряжень дуг радіусів R₁ і R₂ знаходять з’єднуючи точки M' з точками О'₁ і О'₂ та продовжуючи прямі до перетину з дугами N'D'N' та N'С'N.'

Таким же чином будують аксонометричні проекції геометричних тіл.

Приклад послідовності виконання аксонометричного зображення геометричного тіла.

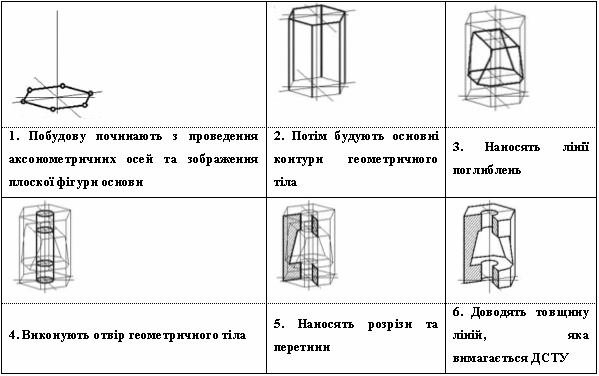
Побудова аксонометрії об’ємних фігур. Необхідно побудувати, наприклад, аксонометрію правильної призми з отвором за її ортогональними проекціями. Оскільки основою призми є квадрат з вершинами на горизонтальних осях, то для забезпечення наочності зображення доцільно звернутися, наприклад, до прямокутної диметрії.

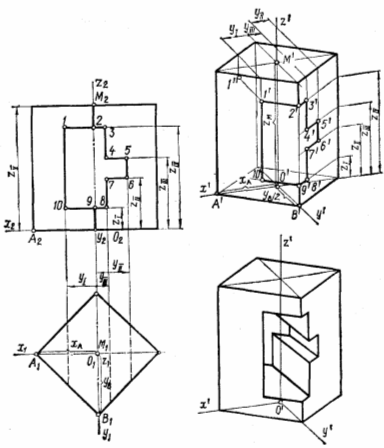
Побудову виконують у такій послідовності.

1. Наносять ортогональні осі на горизонтальній і фронтальній проекціях, будують диметричну проекцію осей.

2. Будують об’єм призми в цілому: спочатку точки А і В та симетричні їм точки. Сполучивши їх, одержують аксонометрію нижньої основи. Вимірюють висоту призми і відкладають цю величину уздовж осі аплікат від точки О, визначивши точку М. Через точку М проводять аксонометричні осі і будують верхню основу призми. Проводять вертикальні ребра.