Скачать

Аберрации оптических систем

Аберрации оптических систем (от лат. Aberratio – уклонение), искажения, погрешности изображения, формулируемых оптическими системами. Аберрации оптических систем проявляются в том, что оптические изображения не вполне отчетливы, не точно соответствуют объектам, или оказываются окрашенными. Наиболее распространены следующие виды аберраций оптических систем: сферическая – недостаток изображения, при котором испущенные одной точкой объекта световые лучи, прошедшие вблизи оптической оси системы, и лучи, прошедшие через отдаленные от оси части системы, не собираются в одну точку: кома – аберрация, возникающая при косом прохождении световых лучей через оптическую систему. Если при прохождении оптической системы сферическая световая волна деформируется так, что пучки лучей, исходящих из одной точки объекта, не пересекаются в одной точке, а располагаются в двух взаимно перпендикулярных отрезках на некотором расстоянии друг от друга, то такие пучки называются астигматическими, а сама эта аберрация – астигматизмом. Аберрация называемая дисторсией, приводит к нарушению геометрического подобия между объектом и его изображением. К аберрациям оптических систем относится также кривизна поля изображения.

Оптические системы могут обладать одновременно несколькими видами аберраций. Их устранение производят в соответствии с назначением системы; часто оно представляет собой трудную задачу. Перечисленные выше аберрации оптических систем называются геометрическими. Существует еще хроматическая аберрация, связанная с зависимостью показателя преломления оптических сред от длины волны света.

1. Хроматическая аберрация

Если пучок немонохроматического света падает на преломляющую поверхность, то он расщепляется на несколько лучей, каждый из которых имеет определенную длину волны. Поэтому, пересекая оптическую систему, лучи света с различными длинами волн будут распространяться после первого преломления не вполне одинаковыми путями. В результате изображение окажется нерезким, и в этом случае говорят, что система обладает хроматической аберрацией.

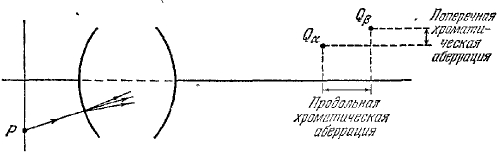
Рис. 1. Продольная и поперечная хроматические аберрации.

Мы ограничимся рассмотрением точек и лучей, расположенных вблизи оси, т. е. предположим, что для каждой длины волны отображение подчиняется законам параксиальной оптики. В этом случае говорят о хроматической аберрации первого порядка, или о первичной аберрации. Пусть  и — отображения точки Р в различных длинах волн (рис. 1); тогда проекции  на направления, параллельное и перпендикулярное оси, определяют соответственно продольную и поперечную хроматические аберрации.

Рассмотрим изменение  фокусного расстояния тонкой линзы в зависимости от изменения показателя преломления . Величина (n - 1)f для такой линзы не зависит от длины волны. Следовательно

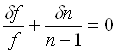 (1)

Величина

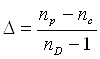 (2)

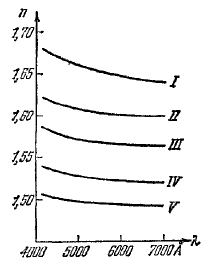
Рис.2. Типичные дисперсионные кривые для стекла различных сортов

I – тяжелый флинт; II – тяжелый бариевый крон;III – легкий флинт;IV – тяжелый крон; V – боросиликатный крон.

где , и  - показатели преломления, соответствующие линиям Фраунгофера F, D и C (4861 , 5893  и 6563 ), служит грубой мерой дисперсии стекла и называется относительной дисперсией. Из (1) видно, что эта величина Приблизительно равна расстоянию между красным и синим изображениями, деленному на фокусное расстояние линзы. На рис. 2 показано изменение величин показателей преломления с изменением длины волны для стекла нескольких сортов, обычно используемых в оптических системах. Соответствующие значения  лежат в пределах от 1/60 до 1/30.

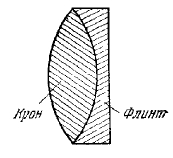
Рис. 3. Ахроматический дуплет

Для получения изображения хорошего качества необходимо, чтобы как монохроматические, так и хроматические аберрации были малы. Обычно выбирают некоторое компромиссное решение, поскольку в общем случае невозможно устранить одновременно аберрации всех типов. Часто оказывается достаточным избавиться от хроматической аберрации для двух выбранных длин волн. Выбор этих длин волн зависит, естественно, от назначения той или иной оптической системы; например, фотообъективы, в отличие от приборов, служащих для визуальных наблюдений, обычно «ахроматизируют» для цветов, близких к синему концу спектра, так как обычная фотографическая пластинка более чувствительна к синей области спектра, чем человеческий глаз. Конечно, ахроматизация для двух длин волн не устраняет полностью цветовую ошибку. Остающаяся хроматическая аберрации называется вторичным спектром.

Рассмотрим теперь условия, при которых две тонкие линзы образуют комбинацию, свободную от хроматизма фокусного расстояния. Величина, обратная фокусному расстоянию комбинации двух тонких линз, расположенных на расстоянии l друг от друга, равна

 (3)

Как мы видим, , когда

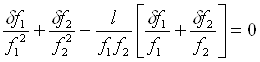 (4)

Если ахроматизация производится для линий C и F, то, используя (1) и (2) получим

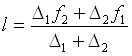 (5)

Где  и  - относительные дисперсии обеих линз.

Один из методов уменьшения хроматической аберрации состоит в использовании двух соприкасающихся тонких линз (рис.3), одна из которых сделана из крона, а вторая из флинта. В этом случае, поскольку l = 0, получим из (5)

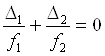 (6)

или, используя (3),

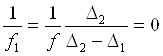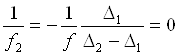 ,  (7)

соотношения (7) для данных сортов стекла и заданного фокусного расстояния  однозначно определяют , и . Но , и  зависят от трех радиусов кривизны, следовательно, величину одного из них можно выбрать произвольно. Эта дополнительная степень свободы позволяет иногда уменьшить до минимума сферическую аберрацию.

Другой способ создании ахроматической системы состоит в использовании двух гонких линз, изготовленных из одинакового стекла (), и расположенных друг от друга на расстоянии, равном полусумме их фокусных расстояний, т. е.

 (8)

Ахроматичность такой комбинации линз следует непосредственно из (5).

В приборе, состоящем на нескольких частей, в общем случае нельзя одновременно устранить хроматизм положения и хроматизм увеличения, если это не сделано для каждой его части. Докажем последнее утверждение для случая двух центрированных тонких линз, разнесенных на расстояние l.

Отображение тонкой линзой является центральной проекцией из ее центра; следовательно (рис. 4),

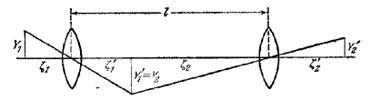
Рис.4. Ахроматизация системы из двух тонких линз

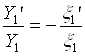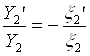,  (9)

Поскольку , находим для увеличения

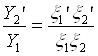 (10)

Если длина волны изменится, то величина  останется той же, величина  также будет прежней, если допустить отсутствие хроматизма положения. Следовательно, условие отсутствия хроматизма увеличения системы можно записать в виде

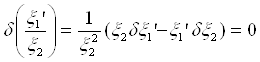 (11)

Так как , , то (11) удовлетворяется лишь при , т.е. если каждая из этих линз ахроматизирована.

2. Волновые и лучевые аберрации, функции аберраций

Рассмотрим вращательно-симметричную оптическую систему. Пусть ,  и , - точки пересечения луча, выходящего из точки предмета , соответственно с плоскостью входного зрачка, плоскостью выходного зрачка и плоскостью параксиального изображения. Если  - параксиальное изображение точки  то вектор  называется аберрацией луча или просто лучевой аберрацией (рис. 2.1).

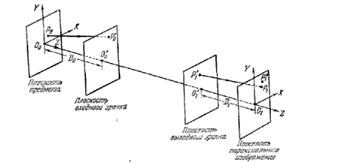
Рис. 2.1. Лучевая аберрация